经历过程,提升抽象概括能力
张秋爽++苏娜

学生学习数学,不仅是要学习那些由前人抽象概括形成的数学知识,同时还要学习抽象概括的方法。反思我们的课堂,为什么有时学生会出现学习知识时无法抽象概括,应用知识时无法举一反三的现象?教师又该如何让学生经历过程,提升他们的抽象概括能力呢?
一、经历直观形象的过程,在认知冲突中提升
计算教学,要让学生理解算理,掌握算法,处理好算理直观和算法抽象之间的关系。以“人教版”《数学》三年级下册《除数是一位数的除法》为例,教师总不能直接告诉学生:竖式的除法计算,从高位除起……为什么加法、减法和乘法的计算都是从个位开始算起,而除法要从高位开始算起呢?作为教师,应该先创设一个现实情境,让学生理解除法的运算意义;接着让学生分小棒;最后把分小棒的过程记录下来就是竖式计算的过程。具体过程如下:
师:有42本故事书,要分给三年级的两个班,每个班分多少本?
生1:42÷2。
师:每个班分多少本?请你用手中的小棒摆一摆。
生2:我先分单根的,把2根平均分成2份,每份是1根;再拿出4捆,每份2捆,合起来是21根。
生3:我先分整捆的,把4捆平均分成2份,每份2捆,也就是2个十;再分单根的,2根平均分成2份,每份是1根,最后分的结果是21根。
师:有的人先分整捆的,有的人先分单根的,都得出了分的结果。谁能把你们分小棒的过程记录下来。
生4:40÷2=20,2÷2=1,20+1=21。
师:你是用口算记录的,还可以用竖式记录,你们试试看。(学生自己尝试,教师讲解。)请看下面的竖式,记录的是先分整捆的,再分单根的操作过程:先分整捆的,把4捆平均分,每人2捆,商是20,2写在十位上。分走了40,整捆的就没有了,还剩下2根,每人1根,1写在个位上,分走了2根,2-2=0,0表示分完了。
(教师边说分的过程,边写竖式,让学生明白每一步的含义。)
生5:先分单根的也可以用竖式记录吗?
师:大家觉得呢?请看下面的竖式,记录的是先分单根再分整捆的操作过程:
对于42÷2,可以先分整捆的,也可以先分单根的,计算上没有什么差别。如果有52本故事书,要分给三年级的两个班,每个班分多少本呢?
有的学生先分整捆,分小棒过程如下,也可以用竖式记录分的过程。
除了先分整捆的以外,也有学生按照自己先前的经验,先分单根再分整捆的,把2根平均分成2份,每份是1根;再拿出4捆,每份2捆;还剩下一捆,平均分成2份,每份是5根,合起来就是26根。用竖式记录如下:
此时产生了认知冲突,计算42÷2时,先分整捆的,或者,先分单根的,竖式记录没有影响,而计算52÷2时,先分单根再分整捆的,竖式记录出现了麻烦,所以,学生自然而然地接受了除法竖式计算从高位算起。
二、经历概念形成的过程,在例证中提升
多举例证,使学生在抽象过程中学会举一反三。在执教《平均分》时,一位年轻的教师以分花的情境导入:把8朵花放在两个花瓶里,可以怎么分?学生根据自己的经验,有了四种不同的分法:8可以分成1和7;8可以分成2和6;8可以分成3和5;8可以分成4和4。像这样,每瓶都放4朵,放得同样多就是平均分。
师:谁能说说什么是平均分?
生1:把8朵花放在两个花瓶里,每个花瓶放4朵就是平均分。
师:谁还能说说什么是平均分?
(这个回答,能看出学生认真听讲了,但教师还期待新的例子。)
生2:把8朵花放在两个花瓶里,每个花瓶放4朵,同样多就是平均分。
师:谁还能说说什么是平均分?
(教师心里不高兴,期待的举一反三没有出现。)
生3:把8朵花放在两个花瓶里,每个花瓶放4朵,同样多就是平均分……
下课了,这名教师开始和师傅抱怨:我们班的学生为什么就不会举一反三呢?师傅告诉她:建立概念的过程需要多举实例,除了正例、反例外,还要有变式。所以,你还需要补充例子:
有9个苹果,平均分给3个小朋友,每人分几个?
有50本书,平均分给50个小朋友,每人分几本?
有10个苹果,平均分给4个小朋友,会有怎样的结果?
教师多举了几个例子后,学生就能渐渐领悟分什么都可以,分多少份都行,只要每份同样多就是平均分。学生经历了不完全归纳的过程,自然而然地抽象概括,并能用自己的话表达对概念的理解。
再如,教学《万以内数加法的竖式计算》,教师需要举多个例子:“123+38”,体会个位相加满十向十位进一;“346+183”,体会十位相加满十向百位进一;“666+444”,体会百位相加满十向千位进一……当然,教师也可以举连续进位的例子,让学生在边计算边总结中逐步总结出“哪一位的数相加满十就要向前一位进一”的算法。虽然教师有时举了很多例子,学生也不一定能顺利总结,教师也要坚持多举实例,让学生经历抽象概括的过程。
三、经历自我建构的过程,在新旧知识联系中提升
《乘法分配律》的学习需要从乘法意义——“几个几”这个旧知识出发,与新知识建立聯系,从而在多个例证中抽象出乘法分配律。
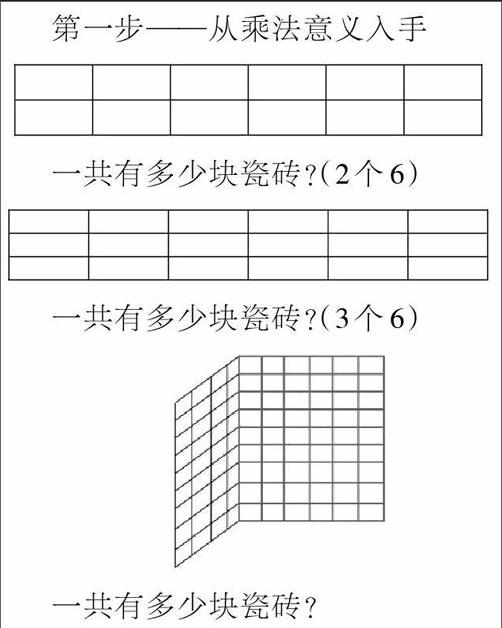
第一步——从乘法意义入手
一共有多少块瓷砖?(2个6)
一共有多少块瓷砖?(3个6)
一共有多少块瓷砖?
学生可以用两种方法来解答:4×9+6×9=90块,或者(6+4)×9=90(块)。所以,4×9+6×9=(6+4)×9。学生从关注结果到关注相等的关系。为什么相等?4个9加上6个9,合起来就是10个9。
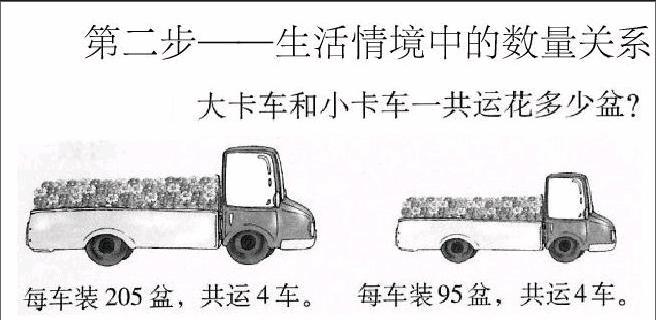
第二步——生活情境中的数量关系
让学生根据自己画的图和列的算式来讲解,说出先求什么,再求什么。教师出示列表:
205×4+95×4=(205+95)×4。左边求的是205个4与95个4的和,右边求的是300个4,所以结果是相等的。
第三步——自己举例子,结构和上述两个例子相同,呈现正例、反例和变式。
生1:我们曾经学过长方形的周长:(长+宽)×2=长×2+宽×2,符合今天学习的内容。
生2:(35+25)×4=35×4+25。
生3:我认为不对,右边的算式中25也应该乘以4。
生4:我们可以从乘法意义来考虑,左边是60个4相加,右边是35个4与25的和,所以两个算式不相等。
举了大量例证后,学生抽象概括出乘法分配律:两个数的和与一个数相乘,可以先把这个数分别与这两个数相乘,再把所得的积加起来。还可以用公式(a+b)×c=a×c+b×c来表示。
四、经历问题解决的过程,在释疑中提升
问题是数学的心脏,让学生从习以为常的生活现象中发现问题、提出问题、分析问题并解决问题。在解决问题中获得对数学本质的理解,从而提升抽象概括能力。
六年级教学“圆的特征”时,教师可以设计如下问题让学生展开探究、讨论:为什么车轮子一般都做成圆形的,做成椭圆的不行吗?为什么马路中间放圆形的井盖,用正方形做井盖不行吗?为什么篮球场上的三分罚球线是半圆的,三角形的不行吗?新年游艺会,请你设计一个套圈游戏的方案,画出草图。
随着四个问题的解决,学生能体会到圆是“一中同长”,其它图形都不是“一中同长”。车轮子做成圆形的,行进时平稳、舒服,做成椭圆形或其它形状的,就会颠簸,不舒服;马路中间的井盖做成圆形的,不论汽车怎样轧,万一翘起来也不会从对角线所在位置掉下去,这样更安全,而做成正方形的井盖,就有可能从对角线的位置掉下去,存在安全隐患;篮球场上的三分罚球线是半圆的,保证在罚球线上的每个位置投球的距离都是一样的,体现了公平性。“圆,一中同长”的本质在生活中有着广泛的应用:为了舒适、为了安全、为了公平……这就是知识的价值,让学生在解决问题中应用知识,感悟数学本质。
教学中还可以采用类比抽象,帮助学生提升抽象概括能力。类比抽象就是进行类比的两类事物,一要了解它们的不同点;二要寻找它们的相同点,从相似点出发,找出解决新问题的方法;三要注意验证。
长方形和长方体是图形家族的成员,它们之间是否有类似的性质呢?
①长方形是特殊的平行四边形,它具有平行四边形的所有性质;长方体是特殊的平行六面体,它具有平行六面体的所有性质。
②长方形的邻边互相垂直,对边互相平行;长方体的邻边互相垂直,相对两面互相平行。
③长方形的对角线互相平分且相等;长方体的对角线互相平分且相等。
④若长a,宽b,对角线l,则有l2=a2+b2;若长方体的长是a,宽是b,高是c,对角线是l,那么l2=a2+b2+c2。
⑤长方形的面积=长×宽;长方体的体积=长×宽×高。
任何一个数学概念都离不开抽象概括。數学概念是现实世界中数量关系和空间形式及其本质属性在思维中的反映。要重视过程,处理好过程和结果的关系;要重视直观,处理好直观和抽象的关系;要重视经验,处理好直接经验和间接经验的关系。让学生经历操作、体验、联系、困惑、猜想、验证、释疑、推理、应用的过程,有助于提升他们的抽象概括能力。

