初中生几何语言学习的障碍分析及应对策略

谭志平

[摘要]几何语言是表达科学思想的语言，更是表示数学思维的载体。因为它的表达方式很特殊，所以初中生在几何语言学习中存在一些障碍，数学教师应根据学生的几何语言学习障碍，探索应对策略，切实提高教学效率。

[关键词]几何语言；障碍；应对策略；初中生

[中图分类号]G633.6 [文献标识码]A [文章编号]1674-6058（2017）05-0024-02

几何语言是表示几何元素和几何图形性质的符号语言，是表达科学思想的语言，更是表示数学思维的载体，它包括文字语言、图形语言和符号语言。文字语言顾名思义就是纯文字表达的几何语言，数学定义、定理、公理及重要结论通常是用文字语言来进行表述。符号语言具有简洁、严谨、通用等特点，符号语言的运用给纷繁复杂的几何证明提供了简明扼要的工具。而图形语言则是联系文字语言和符号语言的一个环节，更有利于学生形象记忆。几何语言掌握得好坏直接影响到数学思维的发展，也直接显示出学生的几何学习水平。新课程标准对学生认识和运用几何语言方面的要求也逐步加强。因此，在初中数学教学中，教师要加强学生几何语言的训练，消除学生学习几何语言时存在的障碍。

通过教学实践，笔者发现初中生在几何语言学习中存在“不会说话”“不会运用符号”“不会识图”三个障碍，针对于此，笔者提出以下几点策略。

一、解决“不会说话”问题

任何一门学科都有它独特的语言特色，几何语言也是如此，它具有高度的简明性和严谨性。美国数学教育学家梅耶（Mayer）曾对学生解决问题时产生困难的原因进行过深入的研究，并指出学生在解决问题时发生困难的原因之一是缺乏转换问题语言的能力。数学教师在批改几何证明题作业时，最害怕遇见那种会证明但由于语言组织存在问题，导致证明过程拖沓冗长或漏洞百出的情况。有的学生在课堂上回答问题时思路很清楚，但不能准确地用几何语言组织解答过程。这就要求教师在课堂上注重几何语言的教学。尤其是初一学生刚刚接触几何时，教师更要强调一些几何语言的规范性。比如“延长线段AB到点C，使AC=2AB”“过点D作DE⊥AB，垂足为E”等，这些专业的几何术语是学生有效表述几何思维过程的重要前提。

二、解决“不会运用符号”问题

几何符号语言是证题的基本要求，正確地书写证明过程的前提条件是正确运用定理，但有些学生在把定理转化为符号语言时，不能正确剖析定理的题设和结论，导致证明过程出错。

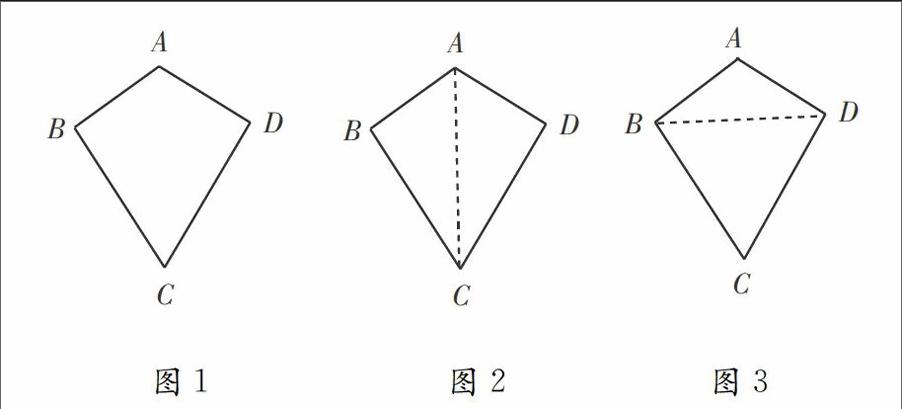
[例1]如图1，在四边形ABCD中，AB=AD，∠B=∠D，求证：BC=DC。

错解：如图2，连接AC，在△ABC和△ADC中，AB=AD，AC=AC，∠B=∠D，所以△ABC≌△ADC，所以BC=DC。

错误原因：在刚开始学习全等三角形的知识时，学生没有准确掌握全等三角形的判定定理，只记住了两边和一角对应相等，并没有注意到这个角必须是两边的夹角。

正解：连接BD，∵AB=AD，∴∠ABD=∠ADB，又∵∠ABC=∠ADC，∴∠CBD=∠CDB，∴BC=DC。

符号语言是文字语言的升华，证明几何题时务必要依照定义、定理等，做到步步有据。教师讲课语言严谨、板书有条理、符号语言书写规范，都能给学生起到示范作用。

三、解决“不会识图”问题

要学好几何必须要有一定的识图能力。图形具有记录作用，可以帮助学生推理演绎、交流论证，所以学生必须要学会从复杂图形中寻找基本型，即平时在学习过程中总结出来的图形语言。

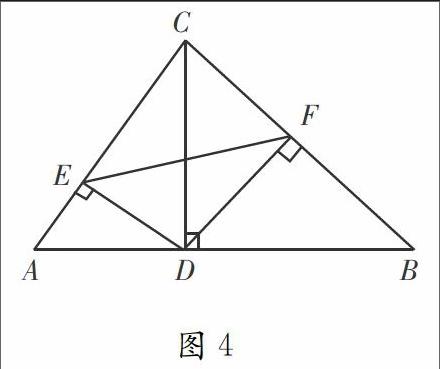
[例2]如图4，在△ABC中，CD⊥AB于D，DE⊥AC于E，DF⊥BC于F。求证：△CEF∽△CBA。

解析：这道题可“从直角三角形被斜边上的高分成的两个直角三角形和原三角形相似”入手，在图4中出现两个这样的基本型（如图5、图6），由此得出CD²=CE·CA，CD²=CF·CB，进而得出CE·CA=CF·CB，即C/CF=CB/CA，再利用“两边对应成比例且夹角相等的两个三角形相似”就能证明△CEF∽△CBA。

当然，如果学生能识别“四点共圆”这个基本几何图形，也能很快解决问题。如图7，因为DE⊥AC于E，DF⊥BC于F，利用“直角三角形斜边上的中线等于斜边的一半”，很容易证得C、E、D、F四点共圆，进而证得∠1=∠2，又易证明∠2=∠B，所以∠1=∠B，再利用“两角对应相等的两个三角形相似”就能证明△CEF∽△CBA。

数学教师在平时的课堂上应注重基本图形的教学，将这些基本型转化为图形语言，灌输到学生的大脑中，从而提高学生解决几何问题的能力。

以上笔者简要分析了初中生在学习几何语言方面所存在的障碍及应对策略，笔者将在今后的教学中继续完善这方面的内容。

（责任编辑 钟伟芳）