水液滴撞击导流面成膜过程数值模拟

马英杰,郝继光

(北京理工大学 宇航学院，北京 100081)

【基础理论与应用研究】

水液滴撞击导流面成膜过程数值模拟

马英杰,郝继光

(北京理工大学 宇航学院，北京 100081)

对液滴撞击亲水导流壁面后的液膜形成过程进行了理论分析，用基于CLSVOF方法的数值模型，分析了液滴撞击亲水表面后的铺展特性，研究了不同表面张力系数和液滴直径对液滴撞击亲水表面润湿直径的影响。结果表明， CLSVOF方法可以用于液滴撞击亲水导流壁面的模拟；液滴撞击壁面达到最大润湿直径的时间随着表面张力系数的增大而减小；液滴撞击在亲水壁面上的最大润湿直径随着液滴初始直径的增大而增大，液滴完成一次铺展收缩过程需要的时间也随液滴初始直径的增大而增加；为进一步研究液滴撞击导流壁面成膜对导流壁面的保护作用提供了理论基础。

液滴撞击；CLSVOF；表面张力系数；液滴直径

航天发射的很多场合都有注水到高温超音速气体射流减少其伴生危害的应用，如航天发射场注水降低燃气射流温度和噪声，导弹热发射时注水降低燃气射流及反溅流辐射的红外信号，燃气蒸汽式弹射器内注水降低燃气射流温度等。研究液滴撞击亲水表面过程对于了解液膜降温效果具有重要意义，液滴撞击导流或发射筒壁面，这些壁面均为亲水表面，研究液滴撞击导流面即研究液滴撞击亲水壁面的铺展过程。液滴撞击壁面铺展是多相流的重要基础过程，是自Worthington[1]首次研究液滴撞击壁面一个多世纪以来，研究者感兴趣的研究对象。影响液滴撞击壁面后的运动和形态的因素有很多，主要有液滴的物性(密度、黏度、表面张力系数、尺寸)、壁面条件、液滴与壁面间的相互作用、液滴碰撞速度、撞击方向、环境压力和温度等因素。本文主要对液滴的物性参数中的表面张力系数和液滴直径对液滴撞击壁面的影响进行了数值模拟研究，阐明了液滴撞壁铺展过程的机理，为其在航天发射领域的应用提供了理论依据和研究方法。

近年来，国内外研究者对液滴撞壁铺展过程进行了大量研究。实验研究方面，1876年Worthinton[1]首先实验研究了液滴撞击金属盘子的过程，后来又研究了牛奶和水银液滴从不同高度落下撞击金属盘子的过程；Mao[2]研究了撞击参数对最大铺展直径和反弹的影响，得出最大铺展直径与Re数、We数和静态接触角的关系；Sikalo等[3-4]实验研究了不同液滴速度、直径、黏性和表面张力系数的液滴撞击石蜡、玻璃壁面铺展直径、速度和高度的变化规律；Wang等[5]实验研究了液滴撞壁铺展高度和铺展直径随时间的变化，得出了不同液滴属性、速度和壁面湿润性对液滴铺展情况不同的影响程度；Radulovic等[6]、Hamraoui等[7]和Fischer等[8]分别研究了pH值、高浓度和低浓度表面活性剂在固体壁面或预置液膜表面上的铺展现象；毕菲菲等[9]用蒸馏水、无水乙醇和甘油3种材料的液滴做了液滴碰撞水平固体壁面的实验，研究了液滴属性对液滴碰壁铺展不同时期的影响；李维仲等[10]实验研究了不同液滴半径、壁面亲疏水性和粗糙度对液滴撞壁铺展过程的影响。数值模拟研究方面，M.Pasandideth- Fard等[11]用实验并基于VOF方法进行了数值模拟，研究了水液滴撞击不锈钢表面的铺展过程，结果与实验结果有很好的一致性；Lunkad等[12]数值模拟研究了碰撞表面的倾斜度、润湿特性、液滴属性和碰撞速度对液滴撞击平壁面和倾斜壁面的铺展动态过程的影响；Gunjal[13]应用VOF方法数值模拟了不同液滴速度、黏度、表面张力和尺寸等对液滴铺展系数和铺展高度的影响，与实验结果基本一致；Kim等[14]用VOF方法数值模拟研究了液滴撞击速度和表面张力等参数对非牛顿流体撞击固体壁面的动态特性的影响。刘邱祖等[15]用格子Boltzmann方法模拟研究了液滴最大铺展直径、壁面亲疏水性与液滴表面张力和铺展速度之间的关系；周龙玉等[16]用实验方法结合数值模拟研究了液滴碰壁铺展和反弹的现象，得出了液滴表面张力系数和液滴半径对其铺展过程的影响；陈石等[17]通过理论分析和数值模拟相结合对液滴受到的惯性力、黏性力和表面张力进行了理论分析，分析了液滴物性参数对液滴撞壁铺展的影响。

本文采用CLSVOF方法对液滴撞击导流壁面成膜过程进行了数值模拟研究，分析了表面张力系数和液滴初始直径对液滴撞壁变形情况和润湿直径的影响，揭示了润湿直径随时间的变化规律。

1 理论基础

1.1 数学模型

本文采用CLSVOF方法即VOF方法和Level Set方法的耦合，该方法即能保证流体的质量守恒又能精确计算界面的曲率和法向，克服了两种方法的不足之处，能对相界面进行更加精确追踪。

连续性方程为

(1)

动量方程为

(2)

表面张力模型表达式为

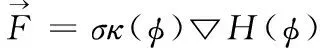
(3)

能量方程为

(4)

1.2 计算模型的建立

采用二维轴对称模型进行计算，所建立的模型如图1所示。

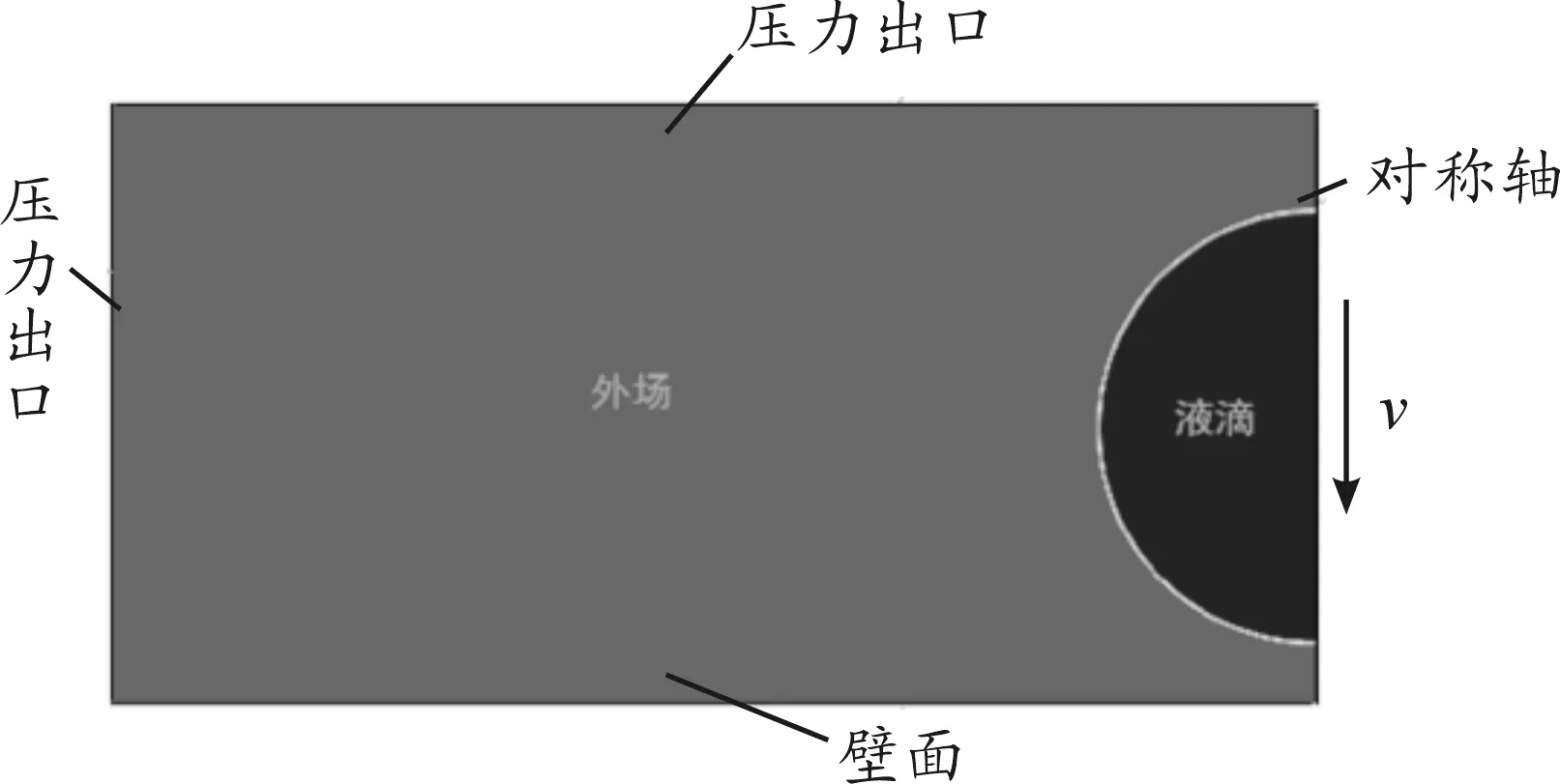
图1 初始时刻模型

图1为初始时刻的计算模型，采用纯水液滴，温度为常温，以一定碰撞速度U0=0.77m/s垂直撞击固体壁面，静态接触角为87.4°。采用有限体积法对控制方程进行离散，压力速度耦合采用SIMPLE方法，压力求解采用PRESTO!方法，计算单元液相体积分数采用Geo-Reconstruct方法离散求解，时间步长Δt=10-6s。

2 计算模型验证

前文确立了基于CLSVOF方法的数值计算模型，在进行数值模拟之前，要进行网格划分，网格数量对计算精度和计算时间有非常关键的影响，因此进行了网格无关性和数值模拟结果的验证。

2.1 无量纲化

量纲定理是E.Buckingham[18]于1951年提出的。根据量纲π定理进行无量纲化。

第一步：写出本问题涉及的所有物理量的量。

T为时间量纲，M为质量量纲，L为长度量纲，表1所示为各物理量量纲中时间、质量和长度量纲的指数，则t和Db可由ρ,D,σ线性表示。

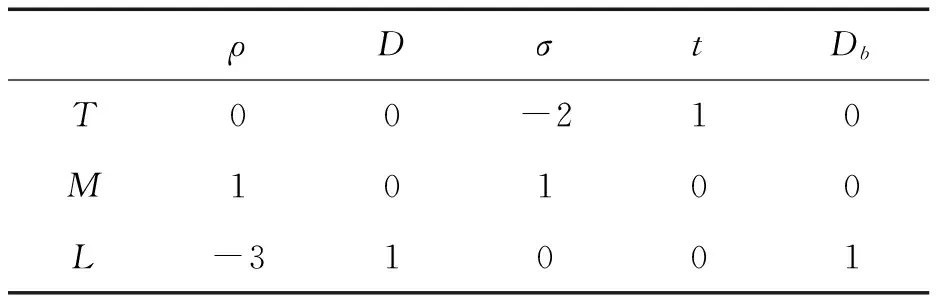
表1 各物理量量纲中时间、质量和长度量纲的指数

第二步，寻找剩余物理量对应的无量纲量。

ln(t)=x1lnρ+x2lnD+x3lnσ

(5)

解出x1,x2,x3，即可得到时间t的无量纲量为

(6)

同理可得润湿直径的无量纲量

(7)

2.2 网格无关性验证

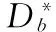
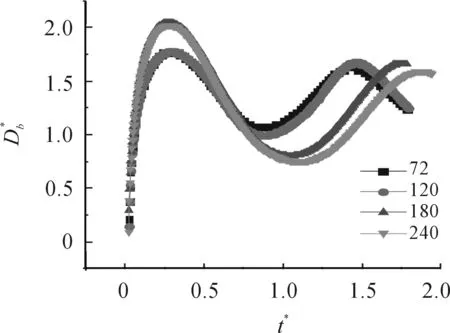
图2 无量纲化后不同网格数量计算的液滴润湿壁面直径随时间的变化

图2为无量纲化后不同网格数量计算的液滴润湿壁面直径随时间的变化。比较了4种不同的网格，其计算结果变化趋势比较相似，只是数值上略有不同，随着网格数量的减少，其计算结果与网格数为240的网格的计算结果差距越大，而且考虑到随着网格数量的增加，需要消耗更多的计算时间，综合以上考虑，本文最终选用网格数为180的网格为计算网格。

2.3 数值模拟结果验证

为了验证所建立的液滴撞击固体壁面模型的准确性，本文将数值模拟结果与实验值进行了对比。实验验证基准采用的是H.Y.Kim等[19]的亲水表面的液滴沉积实验结果。

图3为网格数为180时液滴撞击壁面数值模拟结果与实验结果对比图。可以见到，在整个过程中数值模拟结果与实验结果变化趋势有很好的一致性，但有一定的误差。因为数值模拟计算时，所有初始条件均可瞬时实现，而具体的实验操作有实验条件限制，并且实验装置的操作误差和外界环境条件也是造成误差的原因。数值模拟误差在允许范围之内，通过对液滴撞击壁面过程所建模型的验证，说明所建模型设置合理，所得结果较为准确，因此可以模拟液滴撞壁铺展的实际过程。

图3 网格数为180时液滴撞击壁面数值模拟结果与实验结果对比

3 结果分析

液滴撞击亲水导流壁面的影响因素很多，本项目研究的是不同表面张力系数和不同液滴直径对液滴撞击亲水壁面的影响。

3.1 不同表面张力系数的影响

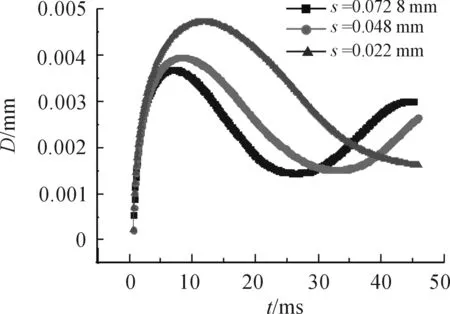
要研究表面张力系数的影响，取液滴速度v=0.77 m/s，初始液滴直径为D=3.6 mm，表面张力系数分别取σ=0.022 N/m、0.048 N/m、0.072 8 N/m。

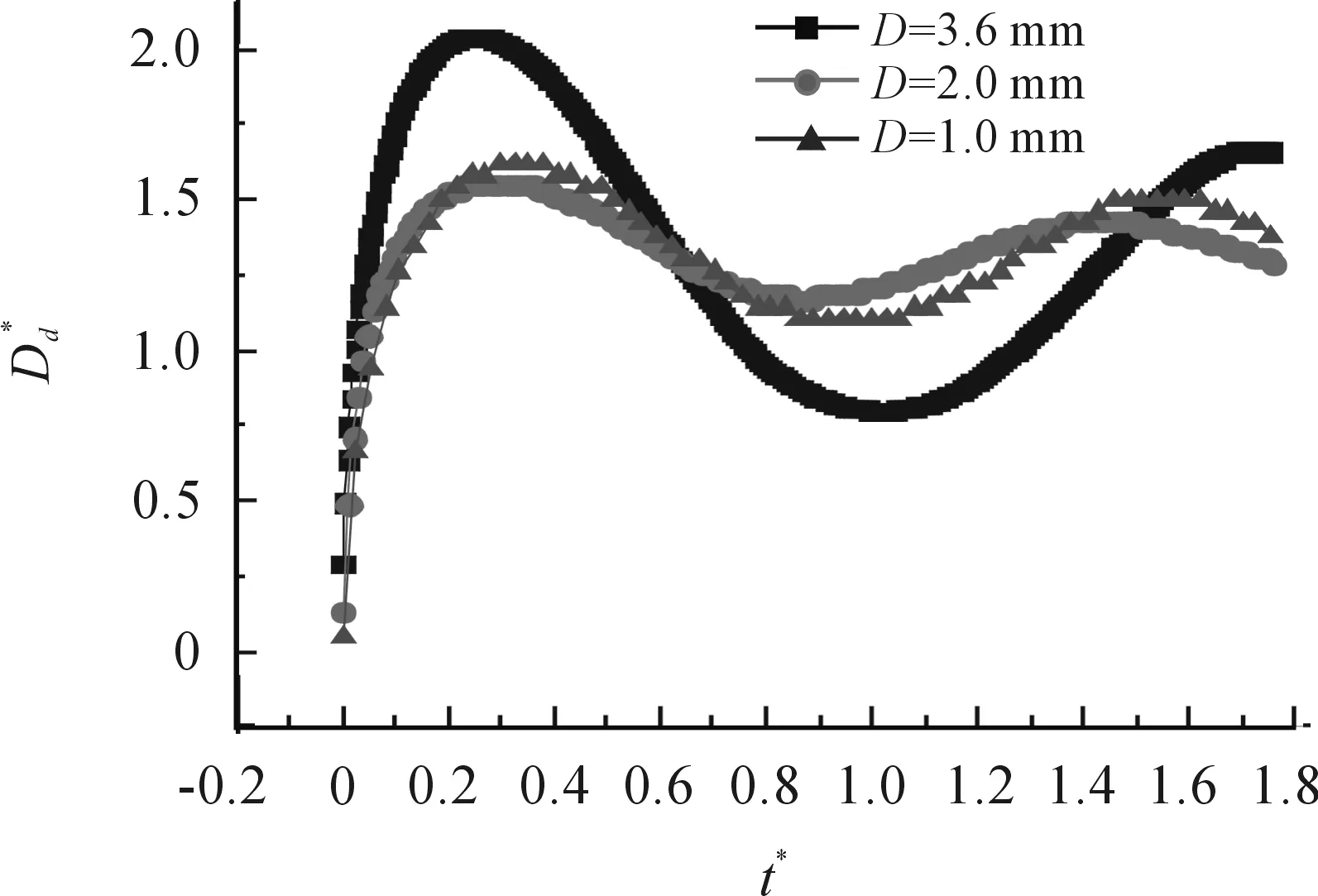
图4为不同表面张力系数的液滴撞壁后形状随时间的变化。可以看出，在撞击开始阶段，3种表面张力下的液滴形状差别不大，到23 ms时，3种液滴都处于收缩状态，液滴润湿直径大小顺序为Db(σ=0.022 N/m)>Db(σ=0.048 N/m)>Db(σ=0.072 8 N/m)的液滴处于收缩状态，另两种液滴处于铺展状态，液滴润湿直径大小顺序为Db(σ=0.022 N/m)

图5为不同表面张力系数液滴撞击壁面润湿直径随时间的变化。可以看出，液滴撞击导流面第一次铺展过程中达到最大润湿直径的时间随着表面张力系数的增大而减小，相应的液滴对导流壁面的降温效果也会更好。将液滴的一个运动周期(如0～26 ms)分成铺展阶段和收缩阶段。因为有表面张力的存在，液滴在铺展过程中会克服表面张力做功，在相同的速度下，液滴初始能量是相同的，表面张力越大，液滴运动会为克服表面张力消耗更多的能量。因此液滴在铺展状态时，液滴最大铺展直径越小，用的时间越少；在收缩阶段，表面张力越大，液滴收缩越快，而且在铺展阶段的最大铺展直径越大，在收缩时会消耗更多的时间。液滴在导流壁面上铺展的速度越快，到达高温区域的速度越快，可以更高效地达到降温效果，更好地保护导流壁面。

图4 不同表面张力系数的液滴撞壁后形状随时间的变化

图5 不同表面张力系数液滴撞击壁面润湿直径Db随时间t的变化

图6为无量纲化后液滴撞击壁面润湿直径随时间的变化。可以看出，3条曲线有很好的同步性，说明无量纲化后3条曲线频率一致。

3.2 不同液滴直径的影响

要研究液滴直径的影响，取液滴速度v=0.77 m/s，表面张力系数σ=0.072 8 N/mm，液滴直径分别取3.6 mm、2 mm和1 mm。

图7为不同直径液滴撞击壁面的润湿直径随时间的变化。可以看出，随着液滴直径的增大，液滴在壁面上的润湿直径变化幅度增大，液滴一次铺展收缩的时间也会相应增加，相应的液滴降温效果会更好。3.6 mm的液滴一次铺展收缩的时间约为26 ms，2 mm的液滴一次铺展收缩的时间约为9.7 ms，1 mm的液滴一次铺展收缩的时间约为4 ms。随着时间增加，曲线趋于平缓，说明液滴在逐渐停止铺展收缩，趋于静止。因为液滴在壁面上铺展达到的最大润湿直径越大，可以覆盖更大的区域，相同数量的液滴可以铺展更大的范围，就可以保护更大范围的导流壁面；而且液滴铺展收缩的速度越慢，与导流壁面的接触时间越长，足够的相同时间内也会使接触面积更大，对导流壁面的保护作用更好。

图6 无量纲化后不同表面张力系数液滴撞击壁面润湿直径随时间t*的变化

图7 不同直径液滴撞击壁面的润湿直径Db随时间t的变化

图8为无量纲化后不同直径液滴撞击壁面的润湿直径随时间的变化。可以看出，3条曲线有很好的同步性，说明无量纲化后3条曲线频率一致。

图8 无量纲化后不同直径液滴撞击壁面的润湿直径随时间t*的变化

随着液滴直径的增加，液滴达到稳定状态就需要更多的时间，因为液滴直径越大初始动能越大，液滴表面张力需要做更多的功才能抵消掉这部分动能；液滴直径越大，铺展收缩一次需要更多的时间，也是这个原理。图7中曲线的每一次振荡都比前一次振荡幅值减小，而且振荡的时间增大，是液滴克服表面张力做功，能量逐渐降低的结果。图7中可以观察到曲线的变化和弹簧系统的变化曲线非常相像，可以把液滴撞击壁面过程类比弹簧系统，液滴有不同的初始速度相当于给弹簧加了不同大小的初始扰动，表面张力就相当于弹簧张力，可以类比弹簧的工作原理解释一些现象。

4 结论

1) 通过与其他文献中的实验结果比较，证明CLSVOF方法可以用于液滴撞击导流面模拟；

2) 液滴撞击导流面形成液膜达到最大润湿直径的时间随着表面张力系数的增大而减小，液滴对导流面的降温效果更好；液滴撞击在亲水导流壁面上的最大润湿直径随着液滴初始直径的增大而增大，形成的液膜对导流壁面的保护作用更好；液滴的完成一次铺展收缩过程需要的时间也随液滴初始直径的增大而增加，液滴对导流壁面的降温效果也更好；

3) 无量纲化后，不同表面张力系数和不同初始直径的液滴润湿直径随时间的变化曲线有很好的同步性，频率一致。

[1] WORTHINGTON A M.On the Forms Assumed by Drops of Liquids Falling Vertically on a Horizontal Plate[J].Royal Society of London Proceedings,1876,25(171/178):261-271.

[2] MAO T,KULMD C S,TRAN H.Spread and Rebound of Liquid Drops upon Impact on Flat Surface[J].ALCHE J,1997,43(9):2169-2179.

[3] SIKALO S,MARENGO M,TROPEA C,et al.Analysis of impact of droplets on horizontal surfaces[J].Experimental Thermal and Fluid Science,25(2002):503-510.

[4] SIKALO S,GANIC E N.Phenomena of Droplet-Surface Interactions[J].Experimental Thermal and Fluid Science,2006,31:97-110.

[5] WANG M J,HUNG Y L,LIN F H.Dynamic behaviors of droplet impact and spreading:a universal relationship study of dimensionless wetting diameter and droplet height[J].Experimental Thermal and Fluid Science,2009,33(7):1112-1118.

[6] RADULOVIC J,SEFIANE K,MARTIN E R，et al.On the effect of PH on spreading of surfactant solutions on hydrophobic surfaces[J].Journal of Colloid and Interface Science,2009,332(2):497-504.

[7] HAMRAOUI A,CACHILE M,POULARD C,et al.Fingering phenomena during spreading of surfactant solution[J].Colloids and Surfaces A Physicochemical and Engineering Aspects,2004,250(1-3):215-221.

[8] FISCHER B J,TROIAN S M.Growth and decay of localized disturbances on a surfactant-coated spreading film[J].Physical Review E,2003,6701(1):6309-6309.

[9] 毕菲菲,郭亚丽,沈胜强,等.液滴撞击固体表面铺展特性的实验研究[J].物理学报,2012,61(18):295-300.

[10]李维仲,朱卫英,权生林,等.液滴撞击水平固体壁面的可视化实验研究[J].热科学与技术,2008,7(2):155-160.

[11]PASANDIDEH-FARD M,AZIZ S D,CHANDRA S,et al.Cooling effectiveness of a water drop impinging on a hot surface[J].International Journal of Heat and Fluid Flow,2001,22:201-210.

[12]LUNKAD S F,BUWA V V,NIGAM K D P.Numerical simulation of drop impact and spreading on horizontal and inclined surfaces[J].Chemical Engineering Science,2007,62(24):7214-7224.

[13]GUNJAL P R,RANADE V V,CHAUDHARI R V.Dynamics of drop impact on solid surface:Experiments and VOF simulations[J].AIChE Journal,2005,51(1):59-78.

[14]EUNJEONG KIM,JEHYUN.Numerical study of the parameters governing the impact dynamics of yield-stress fluid droplets on a solid surface[J].Journal of Non-Newtonian Fluid Mechanics,2012(173):62-71.

[15]刘邱祖,寇子明,韩振南,等.基于格子Boltzmann方法的液滴沿固壁铺展动态过程模拟[J].物理学报,2013,62(23):234701-234701.

[16]周龙玉,田瑞峰.液滴碰撞实验与数值模拟研究[J].原子能科学技术,2014,48(s1):314-319.

[17]陈石,王辉,沈胜强,等.液滴振荡模型及与数值模拟的对比[J].物理学报,2013,62(20):312-317.

[18]BUCKINGHAM E.On Physically Similar Systems; Illustrations of the Use of Dimensional Equations[J].Physical Review,1951,4(4):345-376.

[19]KIM H Y,CHUN J H.The recoiling of liquid droplets upon collision with solid surfaces[J].PHYSICS OF FLUIDS,2001,13(3):643-659.

(责任编辑 杨继森)

Numerical Simulation of Liquid Film Formed by a Water Droplet Impinging onto a Diversion Surface

MA Ying-jie，HAO Ji-guang

(School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

The theory analysis of the liquid film is formed by the droplet impinging on the hydrophilic diversion wall was carried out. With a theoretical model based on the CLSVOF method, the spreading characteristics of droplet impinging on a hydrophilic surface were analyzed. The effects on wetting diameter of different surface tension coefficients and different droplet diameters were researched. The results have shown that the CLSVOF method can be used for the simulation of a droplet impinging on a hydrophilic surface. The time of the droplet impinging on the diversion wall to reach to the maximum wetting diameter decreases as the increase of the surface tension coefficient of the droplet. The maximum wetting diameter of the droplet impinging on a hydrophilic surface increases as the increase of the initial droplet diameter. The time of the droplet spreading and recoiling increases as the increase of droplet diameters. It provides a theoretical basis for the further study of the protective effects of the liquid film formed by the droplet impinging on the diversion wall.

droplet impingement; CLSVOF; surface tension coefficient; droplet diameter

2016-10-20；

2016-11-20 基金项目：自然科学基金(51406012)

马英杰(1991—)，男，硕士研究生,主要从事气液两相流传热传质研究。

郝继光(1979—)，男，讲师，硕士生导师。

10.11809/scbgxb2017.03.039

马英杰,郝继光.水液滴撞击导流面成膜过程数值模拟[J].兵器装备工程学报，2017(3):175-179.

format:MA Ying-jie，HAO Ji-guang.Numerical Simulation of Liquid Film Formed by a Water Droplet Impinging onto a Diversion Surface[J].Journal of Ordnance Equipment Engineering,2017(3):175-179.

TJ760.9

A

2096-2304(2017)03-0175-05