海南岛橡胶风害的重现期预测
刘少军,胡德强,张京红,李伟光,蔡大鑫,张国峰
(海南省气象科学研究所/海南省南海气象防灾减灾重点实验室,海南 海口 570203)
海南岛橡胶风害的重现期预测
刘少军,胡德强,张京红,李伟光,蔡大鑫,张国峰
(海南省气象科学研究所/海南省南海气象防灾减灾重点实验室,海南 海口 570203)
研究大风极值分布的重现期是客观预估橡胶风害强度的有效方法。根据海南岛橡胶种植区1981—2010年逐日最大风速数据,采用极值Ⅰ型算法,模拟了海南岛5、10、20、30、50年一遇最大风速值分布,通过风力与橡胶风害等级表,推断了不同重现期内海南橡胶风害损失分布。结果表明,在5、10、20、30、50年一遇的重现期风速条件下,海南岛橡胶风害损失分别在5%~16%、10%~24%、16%~33%、16%~33%、24%~45%之间,而且分布范围在空间上存在明显差异。
橡胶树;风害;重现期;海南
海南岛是我国主要的橡胶产区,也是台风频发区域。台风是影响海南橡胶树存活以及产胶量的主要自然因素之一[1]。在全球气候变化大背景下,登陆海南岛的台风个数有减少趋势,但总体上台风登陆的平均强度却有增强趋势[2],这必将严重影响到海南岛的橡胶生产。因此,研究橡胶风害的重现期特征对指导橡胶生产具有重要意义。重现期是一个用来描述事件发生可能性的指标,指在相对长时间范围内超过一定强度阈值范围的事件发生的一个稳定周期,是用来表征灾害类事件发生的重要参数[3]。橡胶种植和生产过程,需要了解不同区域可能遇到的风速极值,即不同重现期的最大风速值。极值分布函数是灾害风险管理的有利工具,极值分布函数模型主要分为经典极值理论模型和广义帕累托分布模型[3-4]。对于分布函数形式未知的情况,常采用皮尔逊Ⅲ型分布(Pearson Ⅲ)、韦布尔分布(Weibull)、指数分布(Exponetial)、对数正态分布(Logarithmic normal)、耿贝尔分布(Gumbel)等模拟和拟合极端指数的分布规律。前人研究表明,风速极值的计算采用耿贝尔分布比较合理。孟庆珍等[5]认为耿贝尔法对最大风速进行概率计算效果较好;司奉泰等[6]对菏泽市35种气候值,采用皮尔逊Ⅲ型、对数正态、耿贝尔、韦伯分布函数进行模拟,得到不同分布的适用范围,并认为风速极值应优先考虑使用耿贝尔分布;黄浩辉等[7]利用矩法、极大似然法和耿贝尔法对年极值风速进行了概率计算对比分析,发现多数情况下采用耿贝尔法时拟合效果更好。很多学者采用耿贝尔法推算大风极值,也取得了很好的结果[8-11]。海南橡胶风害率与风速密切相关,不同风速出现的概率必将导致橡胶产生一定的灾害,因而确定不同强度风速的出现概率是进行橡胶风害预测的基础。本研究尝试利用海南岛大风不同重现期预测值,根据统计得到的风力与橡胶风害对应关系,预测不同重现期下橡胶风害率的分布,以期为橡胶生产和防灾减灾提供参考。
1 材料与方法
1.1 数据来源
1981—2010 年气候标准年的海南岛地面气象逐日极大风速数据来源于海南省气象局。海南岛县界行政区数据来源于国家基础地理信息网站提供的1∶4 000 000基础地理信息数据。海南岛橡胶遥感分布数据来源于海南岛TM遥感数据,提取天然橡胶空间分布图,具体方法参考文献[12-13]。
1.2 研究方法
预测海南岛橡胶风害损失重现期的步骤:首先根据海南岛逐日最大风速数据集,采用极值Ⅰ型算法,参数的估算采用耿贝尔法,模拟出不同重现期的最大风速极值分布;然后基于海南岛橡胶遥感分布图和风力大小与橡胶风害对应关系,预测不同重现期内橡胶风害损失,具体流程见图1。
1.2.1 风速极值的计算 计算海南岛不同重现期的最大风速极值采用极值Ⅰ型分布函数[14]:
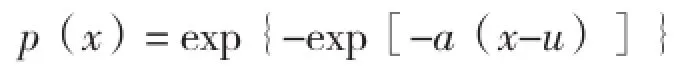
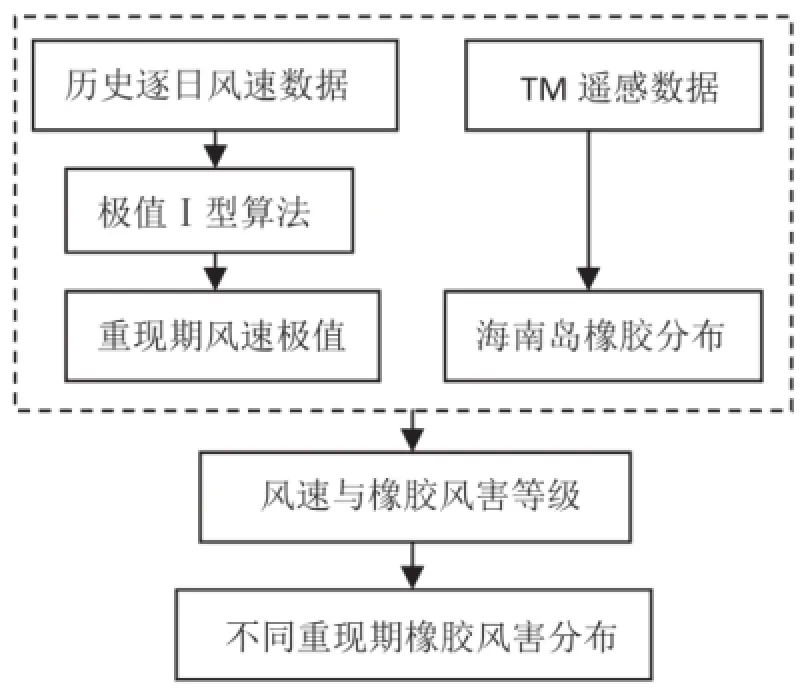
图1 海南橡胶风害损失预估流程
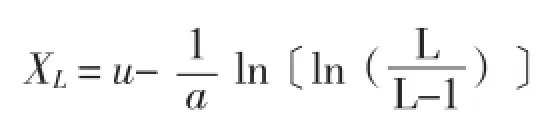
式中,p(x)为概率分布函数,参数X为最大风速,a为分布的尺度参数,u为分布的位置,其中a、u参数的估算采用耿贝尔法[7,15],XL为L年一遇的最大风速。
1.2.2 风力与橡胶风害等级 橡胶风害率随风力增加而增大。一般情况下,当风力小于8级时,橡胶树断倒较少;风力8~9级时,曲线平缓上升;风力达到10级后,曲线急剧上升,断倒率达13%;风力达12级时,断倒率达35%;风力达到15级时,断倒率达69%;风力达16级时,断倒率达84%;风力达17级时,断倒率达100%。大风对橡胶树的损坏程度不仅与大风本身强度有关,还与地形下垫面和橡胶栽培技术等多种因素有关。当风的水平力和橡胶树本身重量产生的垂直重力作用于橡胶树时,会造成橡胶树严重受损[16]。橡胶树风倒现象主要表现为连根拔起、树干折断、根部折断等3种方式,同时遭受风力胁迫的橡胶树产量会下降,死皮会增加[17]。根据海南岛橡胶风害的灾情调查统计结果情况和海南橡胶气象服务实用技术手册,确定橡胶风害与风力评价指标(表1)。
2 结果与分析
本研究根据风力与橡胶风害等级表和不同重现期的最大风速极值,分别得到了5、10、20、30、50年一遇情况下海南岛橡胶风害损失程度。
从图2(封三)可以看出,海南岛橡胶风害5年一遇最大风速极值情况下,橡胶灾害损失范围在5%~16%之间,其中风害率5%~10%主要分布在海南岛北部,风害率10%~16%主要分布在海南岛中部和南部。
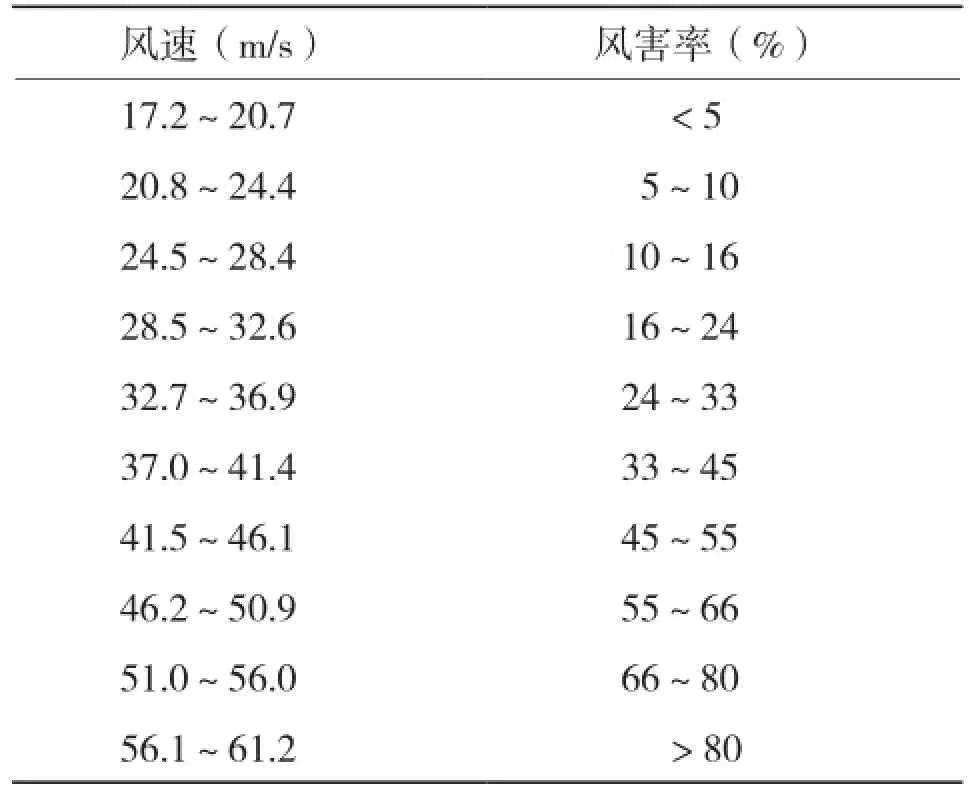
表1 风力与橡胶风害等级[18]
从图3(封三)可以看出,海南岛橡胶风害10年一遇最大风速极值情况下,橡胶灾害损失范围在10%~24%之间,其中风害率10%~16%主要分布在海南岛中部,其他区域风害率为16%~24%。
从图4(封三)可以看出,海南岛橡胶风害20年一遇最大风速极值情况下,橡胶灾害损失范围在16%~33%之间,其中风害率16%~24%主要分布在海南岛中部、南部,风害率24%~33%主要分布在海南岛的北部和东部。
从图5(封三)可以看出,海南岛橡胶风害30年一遇最大风速极值情况下,橡胶灾害损失的范围在16%~33%之间,其中风害率16%~24%主要分布在海南岛中部,风害率24%~33%主要分布在海南岛的四周沿海区域。
从图6(封三)可以看出,海南岛橡胶风害50年一遇最大风速极值情况下,橡胶灾害损失范围在24%~45%之间,其中风害率24%~33%主要分布在海南岛中部、南部,风害率33%~45%主要分布在海南岛的北部和东部。
综上分析可知,随着最大风速极值的增加,海南岛橡胶风害损失程度也随之增加,在空间上也存在一定差异。如20年一遇橡胶风害损失和30年一遇橡胶风害损失虽均在16%~33%之间。但从空间上分布而言,预测的30年一遇橡胶风害损失在24%~33%的空间范围明显大于20年一遇橡胶风害损失的空间分布范围。
3 结论与讨论
风速是决定橡胶林风害损失严重程度的主要因子,当风速增加时,橡胶树受损程度会呈现线性增加趋势[19]。本研究利用最大风速极值出现的概率预估橡胶风害损失的概率,间接通过不同重现期的最大风速极值可能对橡胶造成的损失来预测橡胶风害的空间分布。采用耿贝尔分布函数分别计算5、10、20、30、50年一遇的最大风速极值,并根据风力与橡胶风害对应关系,得到不同重现期的橡胶风害损失分布。从不同重现期的橡胶风害损失图可以看出,随着重现期的增加,橡胶灾害损失的分布范围逐渐从5%~16%上升到24%~45%,而且在空间上的分布也出现了明显差异。由此可以根据橡胶灾害损失的分布规律,合理选择橡胶种植区域,避免盲目种植带来的风灾风险。
虽然从数学意义上讲,最大风速极值作为气候随机变量是不稳定的,但其随时间变化过程在概率分布上却是相对稳定的,因此,最大风速极值的分布可以用分布函数来模拟[20]。耿贝尔分布是极值渐进分布的一种理论模式,由给定的极值求取再现期或由给定的再现期求取再现期极值,需要拟合出概率密度函数。本研究仅利用1981—2010年的最大风速直接采用耿贝尔分布函数估算不同重现期最大风速极值,但对该最大风速极值与更长时间序列的最大风速模拟的重现期最大风速极值是否存在差异,有待进一步检验。
研究表明,当风速大于10级以上,橡胶树的灾损与风速大小正相关,而且橡胶树的风害率明显增加[21]。实际情况下,橡胶风害损失不仅与风速大小有关,而且与地形、橡胶品种、防风措施等密切相关。因此本研究仅考虑橡胶树风害率与最大风速的关系,通过不同重现期最大风速极值对橡胶风害损失进行预测,仅依靠风速的大小来确定灾情,难免存在一定误差。
[1] 江爱良. 青藏高原对我国热带气候及橡胶树种植的影响[J]. 热带地理,2003,23(3):199-203.
[2] 吴慧,林熙,吴胜安. 等. 1949-2005 年海南登陆热带气旋的若干气候变化特征[J]. 气象研究与应用,2010,31(3):9-15.
[3] 李颖,方伟华. 热带气旋降水重现期估算研究[J]. 自然灾害学报,2014,23(6):58-68.
[4] Levine D. Modeling tail behavior with extreme value theory[J]. Risk Management,2009(17):14-18.
[5] 孟庆珍,唐谟智. 成都地面气温与风速年极大值的渐近分布及参数估计[J]. 成都气象学院学报,1997,12(4):284-291.
[6] 司奉泰,刘了凡. 菏泽市气候极值的统计分布和再现期研究[J]. 气象科技,2013,41(6):1091-1094.
[7] 黄浩辉,宋丽莉,植石群等. 广东省风速极值I型分布参数估计方法的比较[J]. 气象,2007,33(3):101-106.
[8] 史军,徐家良,谈建国,等. 上海地区不同重现期的风速估算研究[J]. 地理科学,2015,35(9):1191-1197.
[9] 庞文宝,白光弼,滕跃,等. P-Ⅲ型和极值Ⅰ型分布曲线在最大风速计算中的应用[J]. 气象科技,2009,37(2):221-223.
[10] 王纪军,竹磊磊,胡彩虹,等. 陇海—京广线沿线河南段年最大风速和年最大积雪深度重现期研究[J]. 气象与环境科学,2016,39(3):9-14.
[11] 鹿翠华. 最大风速变化特征及再现期极值估算[J]. 气象科技,2010,38(3):399-402.
[12] 张京红,陶忠良,刘少军,等. 基于TM 影像的海南岛橡胶种植面积信息提取[J]. 热带作物学报,2010,31(4):661-665.
[13] 刘少军,张京红,何政伟. 基于面向对象的橡胶分布面积估算研究[J]. 广东农业科学,2010,37(1):168-170.
[14] 张淑杰,孙立德,马成芝,等. 东北日光温室最大风荷载特征及风灾预警指标研究[J]. 资源科学,2015,37(1):211-218.
[15] 张美花,鲍思钻,曹茜. 用Excel快捷推算重现期气象要素极值的分布[J]. 农技服务,2014(11):109-110.
[16] 刘斌,潘澜,薛立. 台风对森林的影响[J]. 生态学报,2012,32(5):1596-1605.
[17] 杨少琼,莫业勇,范恩伟. 台风对橡胶树的影响[J]. 热带作物学报,1995,16(1):17-28.
[18] 海口市气象局. 海南橡胶气象服务实用技术手册[R]. 2014.
[19] Everham E M,Brokaw N V L. Forest damage and recovery from catastrophic wind[J]. The Botanical Review,1996,62(2):113-185.
[20] 林晶,陈惠,陈家金,等. 福建省年极端低温的分布及其参数估计[J]. 中国农业气象,2011,32(S1):24-27.
[21] 刘少军,张京红,蔡大鑫,等. 海南橡胶林历史台风灾害的时空分布规律研究[J]. 广东农业科学,2015,42(18):132-135.
(责任编辑 崔建勋)
Estimation of return period of rubber wind disaster in Hainan Island
LIU Shao-jun,HU De-qiang,ZHANG Jing-hong,LI Wei-guang,CAI Da-xin,ZHANG Guo-feng
(Hainan Institute of Meteorological Science/ Key Laboratory of South China Sea Meteorological Disaster Prevention and Mitigation of Hainan Province,Haikou 570203,China)
Studying the return period of maximum wind speed is a objective evaluation method of rubber wind damage. Based on the maximum wind speed from 1981 to 2010,the maximum wind speed for 5,10,20,30,50 years return period was calculated in Hainan Island by extreme value type I distribution function. Different return periods of rubber wind damage loss distribution were estimated through wind and rubber wind damage corresponding table. The results showed that in 5,10,20,30,50 years return period of maximum wind speed,the rubber disaster losses ranged from 5% to 16%,10% to 24%,16% to 33%,16% to 33%,24% to 45%,respectively,and the distribution of rubber disaster losses had obvious differences in space.
rubber;wind disaster;return period;Hainan
P49
A
1004-874X(2017)01-0172-04
2016-09-22
国家自然科学基金(41465005,41265007,41675113);海南省自然科学基金(20154172,409005)
刘少军(1980-),男,博士,副研究员,E-mail:cdutlsj@163.com
刘少军,胡德强,张京红,等. 海南岛橡胶风害的重现期预测[J].广东农业科学,2017,44(1):172-175.

