层状结构露天矿边坡稳定的上限解
尹小军, 肖福坤
(黑龙江科技大学 矿业工程学院, 哈尔滨 150022)
层状结构露天矿边坡稳定的上限解
尹小军, 肖福坤
(黑龙江科技大学 矿业工程学院, 哈尔滨 150022)
边坡稳定评估是露天矿开采中最核心的问题之一。基于极限分析上限法,提出两层岩层的露天矿层状边坡垮落机理。不同岩层滑移线是由对数螺旋曲线组成,滑移线共有一个中心点,给出两岩层对数螺旋滑移线的速度。通过对单元块体运动机理和单元块体力学机理分析,根据功能原理,将多个变量的复杂问题转化为单个变量为坡高的函数,利用Matlab 软件,给出稳定率随坡角的变化关系。该研究可以为露天矿边坡设计提供理论依据。
露天矿; 边坡稳定; 临界高度; 层状结构; 上限解
0 引 言
在矿山开采中,露天矿开采占有一定比例。在我国,金属矿露天开采中铁矿占80%~90%[1],有色金属矿占40%~50%,化工材料占 70%,建筑材料占100%,露天煤矿开采比重一直在5%左右。我国现有的16座大型冶金露天矿山已全部转入深部凹陷开采[2],最大凹陷深度将达到或超过500 m,如首钢水厂铁矿最终边坡垂直高度为760 m、最终凹陷开采深度为540 m。在开采过程中,随着坡高和采深的增加,产生的安全性和经济效益问题日益突出。
普遍存在于露天矿且危险最大的变形破坏是滑动,又称滑坡[3]。层状结构露天矿边坡岩体中含有大量节理、裂隙、断层、劈理等复杂的结构面,而边坡失稳、滑动往往是沿着这些结构面发生的。滑动是指完整的岩土体沿其内部一定的面或带,或边坡的松散堆积土沿其基地面(或带)作整体移动。按滑动面形状可分为平面滑动、楔体滑动、圆弧形滑动等。层状结构露天矿边坡的变形是很复杂的。当岩性软弱时,也会形成圆弧形滑动。如准格尔煤田黑代沟露天矿首采区,地层为石炭二叠系煤系地层和马兰黄土等软弱岩土构成,最终滑坡是自重应力作用下形成的弧形破坏面[1]。露天矿的边坡多属层状结构、岩性软弱、强度低,在露天矿开采中,边坡稳定是最核心,也是最复杂的问题。采用一种有效的、便捷的分析方法,研究层状结构露天矿边坡的滑动,分析边坡稳定性,无论是理论研究,还是实际生产都有非常重要的意义。
1 露天矿边坡稳定分析方法
在露天矿的开采中,边坡稳定性是露天矿安全生产的关键技术问题,边坡稳定性分析也是岩石力学研究中的基本问题。露天矿边坡稳定分析的方法主要有以下几种。
1.1 工程地质分析法
该方法[4-6]是通过工程地质勘察,对影响边坡稳定性的主要因素、可能的变形破坏方式、力学机制、变形地质体的成因及其演化史进行分析,得到边坡稳定性状况及其发展趋势的定性说明与解释,其理论基础是地质成因演化论、工程地质类比法及岩体结构控制理论。对于地质条件复杂的矿山岩质边坡,该法在确定滑坡模式和机制方面独具价值[5, 7],为定量研究边坡稳定性奠定了基础。
1.2 极限平衡法
极限平衡法是假设边坡出现滑动面并处于极限平衡状态,然后将边坡离散成有垂直边界的刚体条块,建立条块之间的静力平衡方程,通过求解静力平衡方程得到边坡的安全系数。 基于块体法的极限平衡法通常用于边坡稳定分析[8-10]。陈祖煜等[11]很多学者致力于对条分法的改进。
块体法在分析简化的层状、复杂边坡形状及孔隙水压力的边坡时倍受青睐。但是极限平衡法不能处理运动问题,需要对问题进行大量简化处理,因此,求得的解通常是不太合理的。
1.3 数值模拟法
近年来,数值计算方法取得了迅速发展。有限差分法、有限单元法、离散单元法、边界元法、流形元方法以及不连续变形分析方法等在边坡稳定性分析中得到普遍应用。其中,有限元法的应用最为普遍。1975年Zienkiewice[12]提出了有限元强度折减法(Strength reduction method,SRM),该方法在边坡稳定分析中广泛使用,研究人员[13]采用该方法做了大量边坡稳定性的研究。
1.4 极限分析法
极限分析法[14]是一种有效的稳定性分析方法,它能够明确得出垮落荷载无须逐步进行弹塑性分析,极限分析理论包括上限理论和下限理论,求得的解为相应的上限解和下限解,准确解在上下限围成的面内。极限分析法的应用需要构建[15]运动容许速度场和应力平衡静力场。
用上限法分析边坡稳定问题时,通过构建运动容许速度场,考虑边坡垮落机理。极限分析上限法认为[14],在一个假设的,且满足速度边界条件及应变与速度相容条件的速度场中,由外功率等于所消耗的内能而得到的载荷不小于实际破坏荷载,求得的解为上限解。已有很多研究人员利用极限分析上限法做了大量边坡稳定的研究[16-19],求得在不同情况下的上限解。
然而,由于层状结构露天矿边坡比较高,从几十米到几百米的均有,走向从几百米到数公里,因而边坡剥离的岩层多,各部分地质条件变化大,结构面发育。不同的岩层对边坡稳定性的影响不同。学者们用极限分析上限法研究岩石边坡时,都将滑动块体沿滑移面划分竖直或倾斜的条块状,这样便于问题的求解。实际上,露天矿层状边坡主要是沿已有的层理滑动。文中采用两层岩层边坡垮落模型,以水平状划分,求解露天矿边坡稳定上限解。该方法还可拓展至不同摩擦角和容重的多层岩石边坡稳定的分析。
2 露天矿边坡垮落模型
2.1 问题的定义
露天矿开采时,通常是把矿岩划成一定厚度的水平层,自上而下逐层开采。这种开采的结果使露天矿场的周边形成阶梯状的台阶,多个台阶组成的斜坡构成了露天矿边坡。在分析中,为了简化问题,给出一个露天矿两层岩层的边坡垮落机理,如图1所示。每层的厚度定义为Hi、黏聚力ci、内摩擦角φi、容重γi;分别用下标i=1,2表示,坡面与水平面的倾角为β,定义临界高度Hc。按二维问题处理,即平面应变问题,视为剪切破坏,垮落时向下滑动。
2.2 露天矿边坡垮落模型
滑动面由经过坡趾的不同对数螺旋曲线组成。图1中有二个不同对数螺旋曲线,中心点为O,两层交界面的点上,对数螺旋曲线的半径不变。层状岩层任意对数螺旋曲线的表达式都经过曲线,从而有
r1=r0exp(θ0tanφ1),
r2=r1exp(θ1tanφ2),
式中:r0、r1、r2——弧的半径OB0、OB1、OB2;θ0、θ1——角B0OB1和角B1OB2。
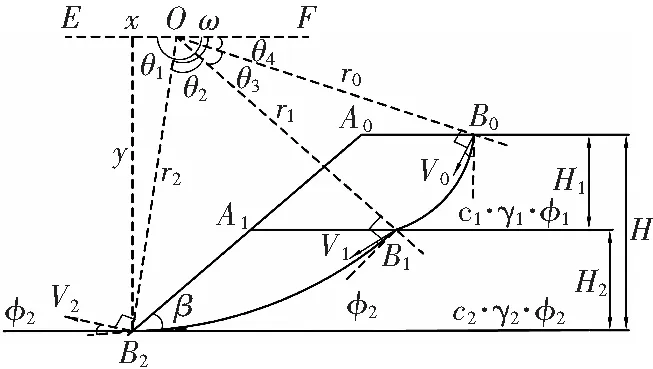
图1 露天矿边坡垮落模型
设角速度为ω,则v0=r0ω,v1=r1ω,边坡高度为H, 倾角为β,用x,y表示水平和竖直方向(用θa、θc表示,即为角B0OF和角FOB2)。
3 露天矿边坡稳定性计算
3.1 单元块体计算分析
单元体受力分析见图2、图3。
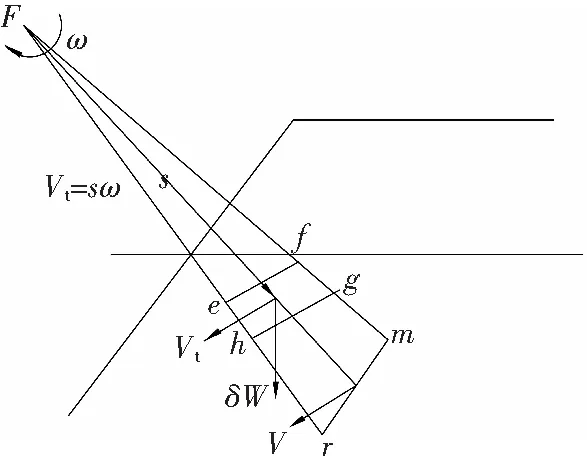
图2 滑动块体单元示意
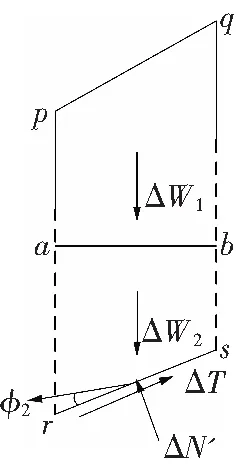
图3 滑动块体受力示意
在给定高度和倾角的露天矿边坡模型中,边坡范围A0A1CB0B1,如果垮落块体的角速度取为ω,在块体内任一点P从O点到径向距离S的合速度vs等于Sω。速度v的方向垂直于径向线FP,通过定义岩石块体A0A1CB0B1的速度,岩石块体单元内部的体力所做的功率为:
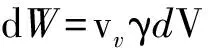
(1)
式(1)中,dV是efghd的体积,vv是单元竖直(向下为正)速度,γ是单元的容重。根据式(1),块体A0A1B2B0B1体力所做的总功率经过积分给出,即:
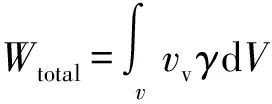
(2)
单元块体内部的能量耗损为
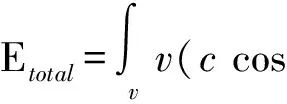
(3)
式(3)中,假设滑动块体之间不分离,v是在任意点滑移面速度增量,c和φ分别是在该点的黏聚力和内摩擦角,dl是沿滑移面单元长度。
ΔW=ΔW1+ΔW2,ΔW1和ΔW2分别为单元abqp和abrs的总重。因此,根据方程(3)体力所做的总功率和块体内部总能量耗损能够确定。如果露天矿边坡处于临界垮落状态,则满足该条件:Etotal=Wtotal;如果给定θa、θc和β,该条件仅能满足特殊的H, 如果Etotal-Wtotal=0,即Etotal=Wtotal,则可求得H。据此,根据给定的β,求得的最小H,即H=Hcr。3.2 上限解的求解
根据极限分析上限理论,为了更简单求解上限解,研究人员[20-22]引入稳定率的概念,或称为稳定系数。
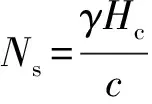
(4)
式中:Ns——边坡的稳定率,量纲1;Hc——边坡临界高度。
通过Etotal=Wtotal, 最终简化为H是函数F问题。
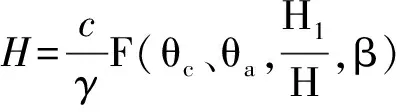
(5)
式(5)中,θa、θc是两个无关参数,使得函数F取得最小值。利用Matlab软件,通过编程,求解多变量方程(5)时,利用式(4)减少多项式的变量,可求解相应的稳定率。
4 结果与分析
稳定率随边坡倾角变化关系见图4。图4a表示φ1=20°,φ2=30°,H1/H= 0、0.2、0.4、0.6、0.8、1.0时,Ns和β的变化关系;同样,图4b表示φ1=20°,φ2=40°时;图4c表示,φ1=30°,φ2=40°时Ns和β的变化关系。
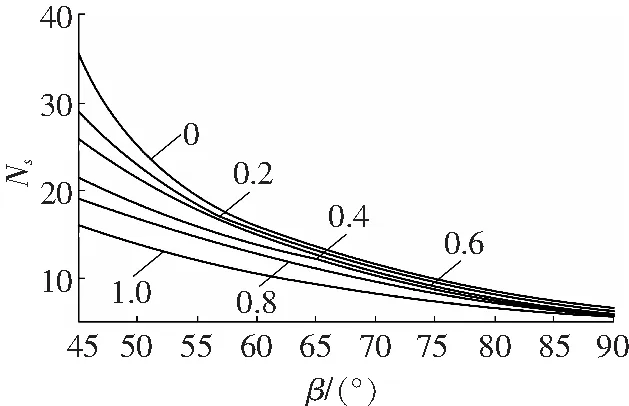
a φ1=20°、φ2=30°
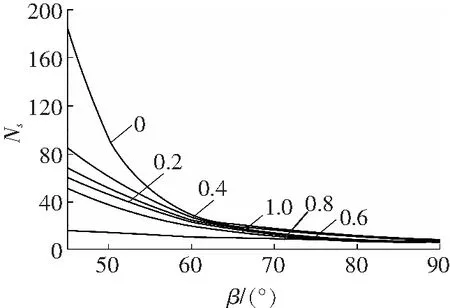
b φ1=20°、φ2=40°
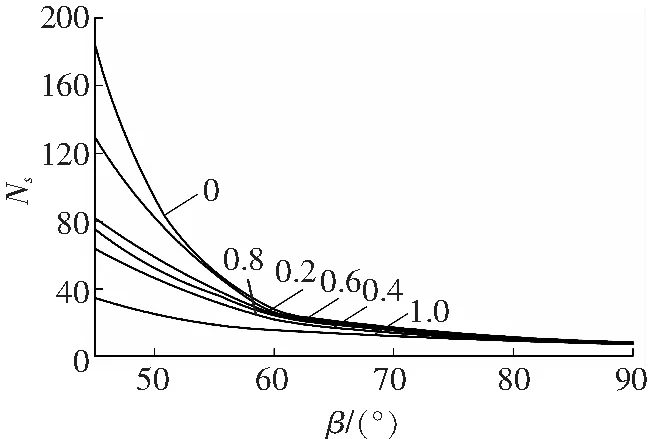
c φ1=20°、φ2=40°
Fig. 4 Variation relationship of stability ratio with slope angle
对提出的两层岩层露天矿边坡垮落机理,计算边坡倾角β从45°到90°,内摩擦角φ1为20°和30°,φ2为30°和40°的稳定率的值。
分析图4可得:
(1)当φ1<φ2时,露天矿边坡的稳定率随H1/H的增加而逐渐减少。
(2)当β较小时,随H1/H的增加,稳定率降低非常明显,而β较大时,影响很小。
(3)随着β的增大,也就是在极陡边坡时,稳定率差异很小,而且随着倾角的增加,稳定率趋于稳定。
(4)φ对稳定率的影响较大。
(5)露天矿边坡倾角β在实际中不能取90°,β的最大取值不属于本研究范围。
5 结束语
笔者对露天矿边坡进行简化,提出含两层岩层的边坡垮落机理,利用极限分析上限法,给出了两层岩层的露天矿边坡垮落机理的稳定率。根据岩体中的层面,采用极限分析上限法确定滑移线,是一种可行的方法。此外,还可考虑多层岩层边坡的垮落机理。该研究可为露天矿边坡稳定设计和防治提供理论依据。
[1] 孙玉科, 杨志法,丁恩保, 等. 中国露天矿边坡稳定性研究[M]. 北京: 中国科学技术出版社, 1999.
[2] 杨天鸿, 张锋春, 于庆磊, 等. 露天矿高陡边坡稳定性研究现状及发展趋势[J]. 岩土力学, 2011, 32(5): 1437-1451.
[3] 周昌寿, 杜竟中, 郭增涛, 等. 露天矿边坡稳定[M]. 徐州: 中国矿业大学出版社, 1990.
[4] 孙玉科, 李建国. 岩质边坡稳定性的工程地质研究[J]. 地质科学, 1965(4): 330-352.
[5] 孙玉科, 倪会宠, 姚宝魁. 边坡岩体稳定性分析[M]. 北京: 科学出版社, 1988.
[6] 孙广忠. 岩体结构力学[M]. 北京: 科学出版社, 1988.
[7] 孙玉科, 姚宝魁. 我国岩质边坡变形破坏的主要地质模式[J]. 岩石力学与工程学报, 1983, 2(1): 67-76.
[8] Bishop A W, Morgenstern N R. Stability coefficients for earth slopes[J]. Geotechnique, 1960, 10(4):129-150.
[9] Sarma S K. Stability analysis of embankments and slope[J].Journal of Geotechnical Engineering, 1979, 105(3): 1511-1524.
[10] 刘汉东, 贾金禄. 岩土工程数值计算方法[M]. 郑州: 黄河水利出版社, 1998.
[11] Chen Z Y , Mogenstern N R. Extensions of the generalized method of slices of stability analysis[J].Canadian Geotechnical Journal, 1983, 20(l): 104-119.
[12] Zienkiewicz O C , Humpheson C , Lewis R W. Associated and nonassociated visco-plasticity and plasticity in soil mechanics[J]. Geotechnique, 1975, 25(4): 671-689.
[13] Dawson E M, Roth W H, Drescher A. Slope stability analysis by strength reduction[J]. Geotechnique, 1999, 49(6): 835-840.
[14] Chen W F. Limit analysis and soil plasticity [M]. Amsterdam: Elsevier, 1975.
[15] Shield R J, Drucker D C. The application of limit analysis to punch indentation problems [J].Journal of Applied Mechanics, 1953, 20(3): 453-460.
[16] Chen W F , Liu X L. Limit analysis in soil mechanics[M]. Amsterdam: Elsevier, 1990.
[17] Chen W F , Fang H Y. On the limit analysis of stability of slopes[J]. Soils and Foundations, 1969, 9(4): 23-32.
[18] Michalowski R L. Slope stability analysis: a kinematical approach[J]. Geotechnique, 1995, 45(2): 283-293.
[19] Kumar J. Slope stability calculations using limit analyses[J].ASCE Special Publication, 2000, 10(1): 239-249.
[20] Taylor D W. Fundamental of soil mechanics[M].New York:John Wiley, 1948.
[21] Britto A M, Kusakabe O. Stability of unsupported axisymmetric excavations in soft clay[J]. Geotechnique, 1982, 32(3): 71-74.
[22] Davis E H, Gunn M J, Mair R J. The stability of shallow tunnel and underground openings in cohesive material [J]. Geotechnique, 1980, 30 (4): 397-416.
(编辑 晁晓筠 校对 李德根)
Research on upper bound solution of layered slope stability for surface mines
YinXiaojun,XiaoFukun
(School of Mining Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China )
The assessment of the stability of slope poses one of the most notorious challenges in surface operation. This paper proposes a novel mechanism behind the slopes collapse of two layered rocks occurring in surface mines, using upper bound limit analysis method and highlights that the sliding surface behaves as a combination of different logarithmic spiral arcs with a common focus. The study drawing on the analysis of the movement mechanism and mechanical mechanism of the element blocks is focused on using principle of work and energy to transmute the complicated problem including multiple variables into the slope height of single variable function, and concludes that stability ratio varies depending on the slope angles, utilizing Matlab toolbox. The research may provide a theoretical basis for slope design of surface mines.
surface mine; slope stability; critical height; layer structure; upper bound solution
2016-12-01
国家自然科学基金项目(51574115)
尹小军(1980-),男,甘肃省秦安人,讲师,研究方向:工程岩体稳定性分析及数值模拟,E-mail:yinxiaojun800@126.com。
10.3969/j.issn.2095-7262.2017.01.008
TD804
2095-7262(2017)01-0035-04
A

