恒温系统中温度场分布仿真
邵璐先,周美娇
(上海理工大学 光电信息与计算机工程学院,上海 200093)
恒温系统中温度场分布仿真
邵璐先,周美娇
(上海理工大学 光电信息与计算机工程学院,上海 200093)
为解决在超高精度光学加工过程中环境温度分布不均匀,温度场变化过快造成材料热胀冷缩的问题,文中根据热力学基本定律,运用FLUENT软件,通过温度场叠加的基本原理,在FLUENT软件中建立仿真模型,并对溴钨灯的温度场进行数值仿真计算。根据仿真分析,不断优化溴钨灯个数和排列情况,从而得到不同的温度场仿真图形。仿真结果表明,可得到一个较大区域的理想温度场,并在实际运用中得到了切实的验证。
恒温系统;溴钨灯;温度场;FLUENT
在超高精密光学加工测量中,环境条件的影响往往成为制约因素,其中温度是重要因素之一。光栅是光学光谱仪的心脏部分,在光栅的制作过程中,为了避免刻制机所用材料因温度变化而产生的热胀冷缩所产生的误差,因此需要创造一个温度精度高的环境,且保持相对恒定的恒温系统[1-2]。文中通过对某一种光源辐射出的热场进行数值仿真,了解该光源的辐射特性,并利用这个光源,在一个立方体箱子的不同位置上放置这个光源,利用这些光源产生的热场,在恒温箱的底部相互叠加,最终可形成一个相对稳定的恒温区域,制作出一个恒温箱[3]。
1 构建模型
利用FLUENT提供的专用软件Gambit创建一个溴钨灯的数学模型[4]40 W的电能在灯丝内消耗掉。灯丝的一部分热量通过辐射传递,一部分通过自然对流传递。灯丝发出的辐射一部分穿过了灯泡,一部分被反射,一部分被吸收[5]溴钨灯的灯泡用玻璃制成,而镜片。灯座和反射器使用聚碳酸酯制成[6]。
仿真了溴钨灯温度场流动和热模型的设置和求解过程。辐射的计算使用离散坐标模型进行建模。FLUENT的壳层导热功能用于模拟薄金属片的导热,如未划分网格的反射器,灯座和遮板等。网格的划分在Gambit完成,在灯丝上的辐射是高度区域化的,可能需要高达4×4的角度划分。本文中使用了2×2的角度离散处理。也可进行角度离散的敏感性研究,可以在开始时使用2×2的角度离散处理,然后使用4×4角度划分继续计算,直到在主要部件上的最大温度没有明显变化为止[7-8]。
为了避免材料对FLUENT仿真的影响,实验中将仿真模型的反射器部分材料设定为聚碳酸酯材料,将灯泡设定为玻璃材料,将溴钨灯内镜片部分也设定为聚碳酸酯材料,将灯泡外表面涂层设定为涂层材料。
对包围灯座外部圆柱壁面的流体没有进行建模。但该外表也通过自然对流冷却。另外,在外表面和环境之间也存在辐射换热。FLUENT使用牛顿冷却定律如式(1)所示[9]
q=H×(Ts-Tref)
(1)
q=K×ee×(Ts-Te)
(2)
Qr=(1-df)×Qi+df×(1-ei)×Qi
(3)
从而来确定对流产生的热损失。H可通过使用对圆柱体自然对流的Churchill和CHU关系确定。对外部辐射率ee输入的值为0.95。保留外部辐射温度设定的默认值300 K。Fluent用来确定与环境的辐射换热量,如式(2)所示,其中,K为玻尔兹曼常数;Ts是反射器外表面上计算的温度;Te为外部辐射温度;ei为内部辐射率。保留对其他参数的默认值,并关闭面板[10]。
反射器的外表面使用黑涂层,内表面用高反射物质涂覆。尽管如此,内外表面之间还会产生辐射换热。对内部辐射输入0.2。之后设置反射器内表面,若漫反射分数为0,所有的入射辐射都发生镜像反射(如同干净的镜面),其中入射角等于反射角。实际上,反射器并非均是100%的反射,上面可能存在灰尘。入射辐射的反射部分使用式(3)计算:其中,df是漫反射分数,ei为内部发射率。等号右边的第一项是镜向反射部分,第二项是漫射反射部分[5]。
设置速度和压力的值为0,初始温度的值为300 K,在内部上填充高温为500 K,首先通过请求 20次迭代来开始计算过程。由于解现在是稳定的,可将亚松驰因子增加到1.0,这样将明显地加速离散坐标方程的迭代过程。最后在后处理的过程中可以看到所关注的温度场仿真图[11]。
在溴钨灯模型中,上半部分的气体流动速度明显比其他区域要快,说明在溴钨灯内的温度是不均匀的,会发生热传递与对流,灯内上方的空气温度会首先升高,之后通过热传递方式使灯内下方的温度较低的气体的温度升高,同时上方较热的空气也会与下方较冷的空气通过循环流动,最终使整体温度逐渐趋于均匀[9]。
2 恒温系统中广场-热场分布
2.1 创建恒温箱模型
利用上述的溴钨灯来创造出一个恒温箱。大致思路是在一个一立方体的箱体中,通过设置不同的的溴钨灯数量,以及对溴钨灯排布的位置进行调整,从而使其的温度场叠加,在箱的底部形成一个大致的恒温面。
2.2 Matlab仿真
本次仿真利用Matlab软件,且为了方便计算,实验中将每个溴钨灯都看成一个点源,利用点源产生的辐射照度公式[12]
(4)
其中,l为被照面上x点处面积元的距离;θ为法线与l的夹角;I是点源的辐射强度。
而在实际仿真过程中,在Matlab中热传导问题采用抛物型偏微分方程[13-14]

(5)
其中,ρ表示密度;C表示比热;k为导热系数;为热导系数;Q为热源;h表示对留热的传输系数;Text表示环境温度;h(Text-T)表示从环境到区域内部的传输热量。本方程主要用来描述平面图形的热传导问题,并用来描述轴对称三维问题经过降维后的热传导问题[15]。但若仅考虑定态情况,则方程为
-·(kT)=Q+h·(Text-T)
(6)
2.3 灯泡均匀分布
首先将箱体的前后左右4个面上,每个面均匀排布等干个灯泡,以两行3列的形式均匀排列在每个面上。从而得到底部的温度场如图1所示。从图1中可看出,底部的温度场中间部分温度较低,靠近前后左右4个面即靠近光源处的位置温度较高,且整体看上去温度的梯度变较大。
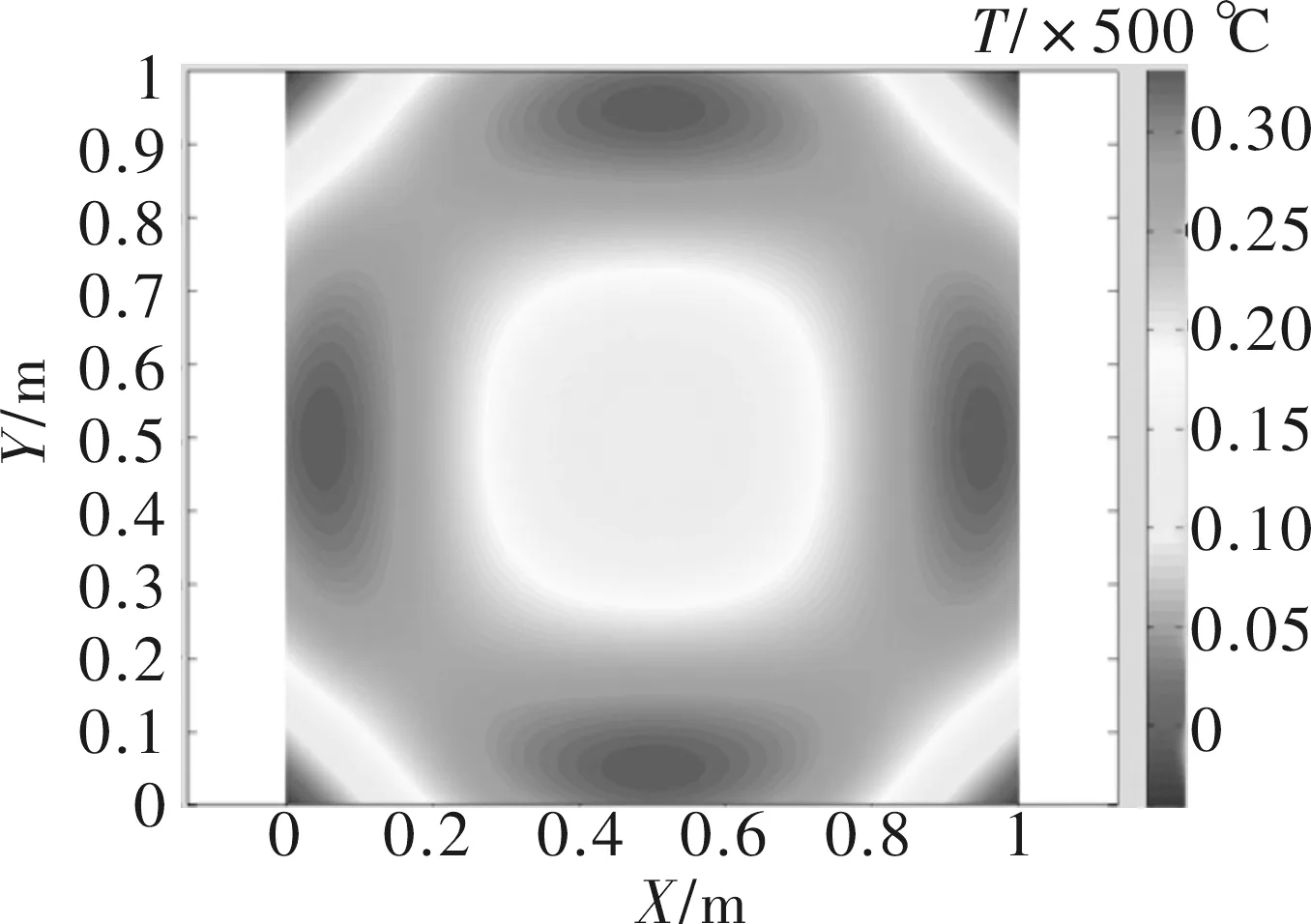
图1 灯泡在四周均匀分布时底部温度场
因此,为了解决这种情况可在箱体的上表面再增加一些点源,从而对箱体底部中央位置较低温度区域进行补充。为此,在箱体的上表面又增加了一组4×4的点源阵,继续进行温度场的仿真,仿真结果如图2所示。
通过图2可看出,箱体的底部的温度场的中央部位的温度得到了明显提高。但整体观察,这个温度场的温度梯度变化依然较大,中央位置的温度仍不够,在靠近4个面的位置温度依然过高,从而造成了整个面的温度梯度变化依然较大,整体的温度很不均匀。

图2 顶部增加4×4点源阵后底部温度场
为解决这一问题,决定继续对顶部点源的数量进行增加,增加到一个5×5的点源阵,增加了点源之后,由于点源在顶部位置,产生的温度场在箱体底部的温度必然中心区域高,而四周的区域底可与现有的温度场进行互补叠加,使中间区域的温度上升较多,而四周区域的温度上升较少,使底部产生的温度场更加均匀,得到仿真结果,如图3所示。

图3 顶部为5×5点源阵时底部温度场
图3所示,在底面位置已得到一小片恒温的区域。但整体而言,这个恒温的区域仍然偏小,在靠近4个面的位置温度依然较高,且四周的温度梯度变化较大,因此并不是一个理想的效果。为此,再增加一组点源来观察一下效果,仿真的结果如图4所示。
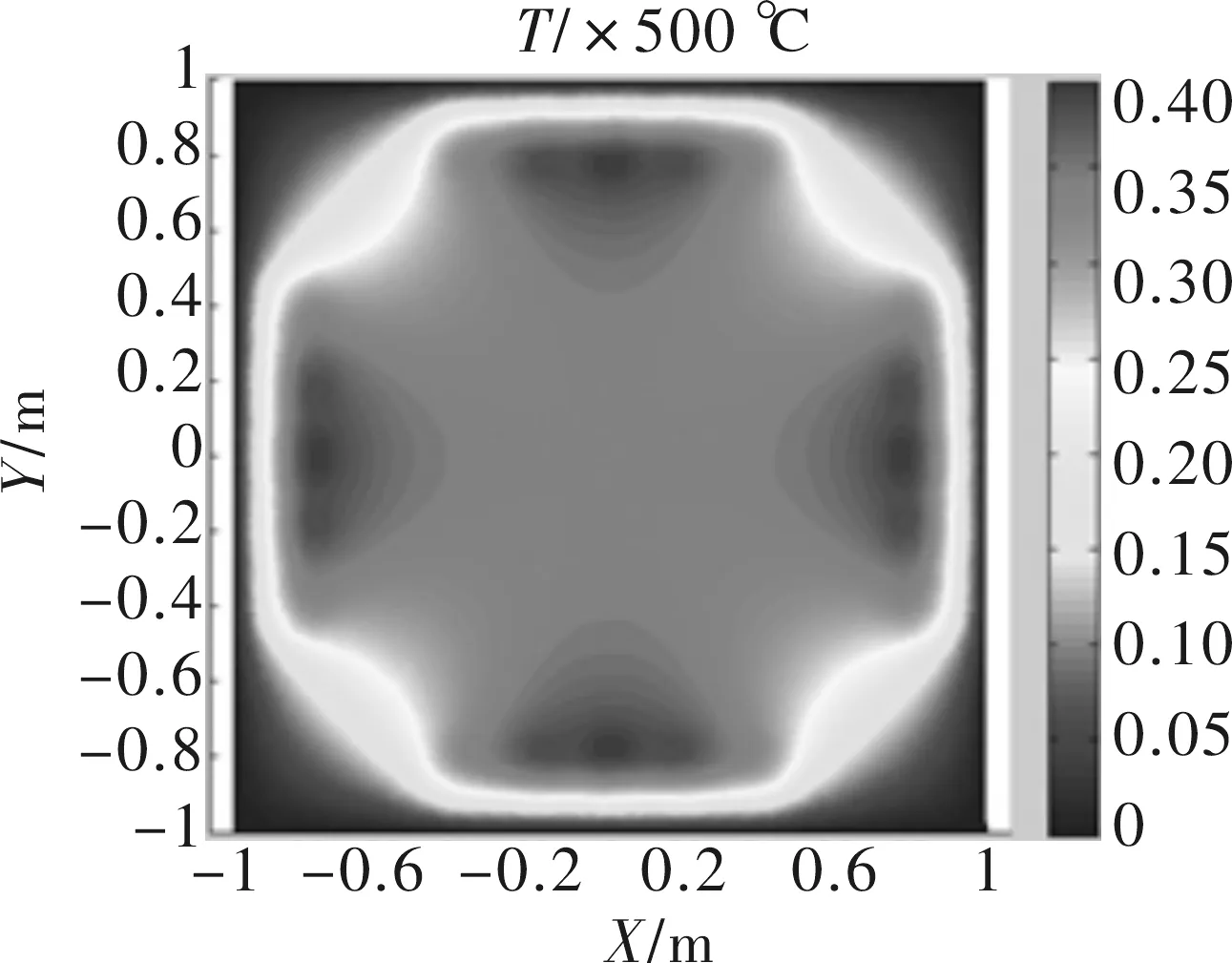
图4 顶部为6×6点源阵时底部温度场
通过再次增加了一组点源之后,使箱体的底部的温度场中央部分的恒温区域明显的增大。验证是否可再增加一组点源来扩大恒温区域,观察一下7×7的情况下的温度场布,图5所示。

图5 顶部为7×7点源阵时底部温度场
通过图5可看出,在箱体的顶部如果排布的点源过多,顶部点源产生的热场过于强大,从而覆盖了箱体四周的点源产生的热场,使得箱体底部的恒温面积反而变得小了,因此也不可取。
3 灯泡最佳分布方式
经过一系列实验以及对箱体底面温度场的仿真,最终确定了当箱体前后左右4个面上的点源分别各自相距移动0.5 m后,顶部排列6×6的点源时,箱体底部的温度场会产生一个最大的恒温区域,温度的变化最小。
可看出此时箱体底部的温度场最为接近一个恒温的状态。此外,可通过继续增加灯泡的数量,以及改变其的分布方式,从而达到更加理想的一个恒温状态。此外,为了得到不同温度的恒温区域,可通过改变灯泡数量及灯泡辐射的强度来达到某一种特定值的恒温效果[12]。
4 结束语
通过Matlab对底面温度场的仿真,可看出当恒温箱中四周4个面上两边的溴钨灯向两边移动后,整体的温度场会相对变得均匀。恒温箱顶部的溴钨灯数量越多,对恒温箱中央部分的温度提升影响越大。通过对恒温箱四周溴钨灯排列位置和顶部溴钨灯数量的变化进行调整,相互作用补充,从而首先在恒温箱底部得到一个较为理想的恒温区域。最后确定了当箱体前后左右4个面上的两边两列点源分别各自相距0.5 m后,顶部排列6×6的点源时,箱体底部的温度场会产生一个最大的恒温区域,温度的变化最小,可产生一个恒温场,恒温区域面积比较大[16],其实物如图6所示。

图6 实际恒温箱灯泡图
通过观察可看出,得到的每一个温度场在4个角的位置温度均较低,若想要得到范围更加广的恒温区域,可继续在4个角的位置排布灯泡,从而提高4个角的周围的区域的温度,使整个面的温度更加均匀。
另一方面,箱体底部的温度场始终处于一种四周偏低中央偏高的情况,且温度场的梯度变化始终较大。因此,通过寻找底部上方一定距离的横截面的温度场,最终可找到一个理想的恒温区域[3]。
若要控制恒温区域的温度,可通过放置不同功率的灯泡的方法来改变灯泡辐射强度,从而产生不同的温度场。可在其中进行光学加工,精密仪器的测量等科学项目,有较高的利用价值。
[1] 李燕青,郝德阜.衍射光栅制造技术的发展[J].长春理工大学学报,2003,26(1):66-68.
[2] 王宪平,李圣怡.超精密环境温度控制及温度测量技术研究[J].中国机械工程,2000,11(8):869-871.
[3] 胡曦.三维场景温度场的仿真研究[D].武汉:华中科技大学,2013.
[4] 王瑞金,张凯,王刚.Fluent技术基础与应用实例[M].北京:清华大学出版社,2007.
[5] 朱自强.应用计算流体力学[M].北京:北京航空航天大学出版社,1998.
[6] 刘霞,葛新锋. FLUENT软件及其在我国的应用[J]. 能源研究与利用,2003(2):36-38.
[7] 王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社,2004.
[8] 方坤.计算流体力学的几种常用软件[J].煤炭技术,2006,25(12):124-125.
[9] 任玉新,陈海听.计算流体力学基础[M].北京:清华大学出版社,2006.
[10] 张辉.微纳米测量环境控制机理及系统研究[D].合肥:合肥工业大学,2009.
[11] 姚征,陈康民.CFD通用软件综述[J].上海理工大学学报,2002,24(2):137-144.
[12] 周志敏,周纪海,纪爱华.LED照明技术与应用电路[M].北京:电子工业出版社,2009.
[13] 韩艳霞,金辉.计算流体力学通用软件-STAR-CD简介[J].甘肃科技,2005(9):70,36.
[14] 陶建兴,杨亚东,孙庆宽.CFD仿真技术在空调房间温度场研究中的应用[J].暖通空调,2002,32(2):95-98.
[15] 孙纪宁.ANSYS CFX对流传热数值模拟基础应用教程[M].北京:国防科技出版社,2010.
[16] 纽春萍,陈德桂,刘颖异,等.交流接触器温度场仿真及影响因素的分析[J].电工技术学报,2007,22(5):71-77.
Distributed Simulation of Light Field and Thermal Field in Thermostat System
SHAO Luxian,ZHOU Meijiao
(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology, Shanghai 200093, China)
In order to solve the problem in the ultra-high precision optical processing of the environment temperature distribution is not uniform, and the material of heat bilges cold shink by the temperature field changed too fast. According to the laws of thermodynamics, and using the FLUENT software, through the principle of superposition of the temperature field, in fluent software established simulation models, And the temperature field of the bromine tungsten lamp by numerical simulation. According to the simulation analysis, constantly optimize the bromine tungsten lamp number and arrangement,then the simulation results of different temperature fields are obtained. The simulation results show that the obtained temperature field in a large area,which has been effectively verified in practical application.
thermostat system; bromine tungsten lamp; temperature field; FLUENT
2016- 03- 09
邵璐先(1989-),男,硕士研究生。研究方向:仪器测量与技术。周美娇(1977-),女,博士,讲师。研究方向:现场总线控制,指纹识别与数等。
10.16180/j.cnki.issn1007-7820.2017.01.043
TP273
A
1007-7820(2017)01-157-04

