GNSS信号中多普勒频移的估计与补偿技术
高法钦,夏海霞
(浙江理工大学 信息学院,浙江 杭州 310018)
GNSS信号中多普勒频移的估计与补偿技术
高法钦,夏海霞
(浙江理工大学 信息学院,浙江 杭州 310018)
为了提高全球导航卫星系统(GNSS)的信号捕获速度,提出了一种校正与补偿由卫星运动导致的GNSS信号中的多普勒频移的算法。讨论了由卫星运动的动力学方程计算卫星运动速度的方法、(GNSS接收机位置下的)可见卫星的确定,分析了由卫星运动引入GNSS信号中的多普勒频移,通过建模仿真了24颗卫星信号的多普勒频移变化曲线。仿真结果表明,多普勒随时间变化的曲线是具有周期性和单值性的光滑曲线,可依据接收机时钟估计出多普勒频移值,在半径800 km左右的范围内,大部分时间上的估计误差小于500 Hz,有效地缩减了多普勒频移的不确定范围,提高了GNSS信号的捕获速度。
GNSS;多普勒频移;搜索范围;捕获速度
0 引言
全球导航卫星系统(GNSS)是一种以卫星为基础的无线电导航系统,能为陆、海、空的各类载体提供全天候、不间断、高精度和实时的导航定位服务[1]。目前,应用最广的GNSS系统是美国的GPS,我国自主研发的GNSS系统——北斗系统(BDS)已于2012年底开始对我国境内及周边地区正式提供定位服务[1]。
GNSS接收机本地解码需要一个与接收信号同频同相的本地载波和伪码[2]。由于多普勒效应等因素的影响,实际接收信号的频率和伪码相位具有不确定性。因此,需要通过捕获和跟踪等同步过程使本地信号与接收信号同步,本文专门研究GNSS信号的捕获,捕获是伪码相位空间和频率空间的二维搜索[3]。

为了提高捕获速度,有人研究了基于傅里叶变换法的并行捕获算法[5]以及它们的一些改进算法[6,7],也有人在此基础上引入最大似然估计[8]、小波变换[9]、拟合法[10]和匹配滤波法[11]等技术,取得了较好的效果。文献[9,12,13]等还研究了低信噪比且高动态情况下的捕获算法,也有文献研究了多径信号的影响[14]。为了进一步提高捕获速度,尤其是弱信号情况下的捕获速度,本文研究如何估计和补偿由卫星运动引入的多普勒频移,缩小捕获搜索空间。
1 卫星位置和速度的计算
多普勒频移是由卫星与接收机之间的相对运动造成的[2],本文讨论卫星运动引入的多普勒频移。为此,需要先讨论卫星的运动状态以及接收机的位置等信息,下面以GPS为例讨论卫星位置和速度的计算。
卫星在空间运行的轨迹称为轨道,而描述卫星轨道位置和状态的参数称为轨道参数,如图1所示。

图1 卫星轨道参数
卫星轨道一般通过一组适宜的参数来描述,这组参数的选择不是唯一的。GPS系统采用开普勒轨道参数:a为轨道椭圆的长半径;e为轨道椭圆的偏心率;Ω为升交点赤经,即在地球赤道平面上升交点与春分点之间的地心夹角,它是卫星由南向北运行时,其轨道通过赤道面的交点;i为轨道倾角,即卫星轨道平面与地球赤道面之间的夹角;为近地点角距,即在轨道平面上升交点与近地点之间的地心角距;f为卫星的真近点角,即在轨道平面上卫星与近地点之间的地心角距。
其中,参数a和e确定了开普勒椭圆的形状和大小;参数Ω和i唯一地确定了卫星轨道平面与地球体之间的相对定向;参数表达了开普勒椭圆在轨道平面上的定向;参数f为时间函数,确定了卫星在轨道上的瞬时位置。通过这6个参数就可以确定出卫星在轨道平面上的瞬间位置。
1.1 卫星位置计算
卫星在地心地固坐标系中的位置(xs,ys,zs),可表示为:xs=rcos(f+ω)cos(Ω-ΩG)-rsin(f+ω)sin(Ω-ΩG)cosi,
ys=rcos(f+ω)sin(Ω-ΩG)+rsin(f+ω)cos(Ω-ΩG)cosi,
zs=rsin(f+ω)sini。
(1)
式中,r为卫星到地心的距离,由于地球的自转,地心地固坐标系也有一个旋转角,表示为:
ΩG=ΩG0+ωe(t-t0)。
(2)
式中,t0为参考时间;ΩG0为参考时间的格林威治子午线的赤经;ωe为地球自转角速度,取ωe=7.292 115 147e-5(rad/s)。在不考虑扰动或摄动的情况下,ΩG0,ωe,Ω,ω都是常数,只有f是时间的函数,由于轨道参数中f时刻在变,所以卫星不是直接播发f值,而是给出卫星在轨道上运行的平均角速率n以及卫星经过所在点的时间t,可以通过下列公式计算f值:
(3)
式中,E为偏近地点角;M为平均近地点角,如果将卫星轨道看作圆形,即令轨道离心率e=0,且取参考时间t0为零,则可得f=nt。
1.2 卫星速度的计算
速度矢量表达式为:

(4)


(5)

(6)
2 可见星及选星计算
可设接收机(用户)位置为接收机记录的上一时刻的位置。在已知载体位置的情况下,可见星是仰角大于0°的卫星。设地心o、用户u、卫星s构成三角形△ous(如图2所示)。

图2 仰角计算示意
三角形△ous周长的一半为:
s=(ou+us+os)/2。
(7)
内切圆半径为:
rn=[(s-ou)(s-os)(s-us)/s]1/2,
(8)
(9)
则仰角为:
(10)
由于电离层和对流层延迟等误差源,若仰角太小,这些因素所造成的测量误差相对于较小的仰角就会很大,故取仰角大于5°的卫星作为可见星。
在选出可见星之后,采用最佳导航星选择的工程算法,从可见星中选出仰角最大的星(天顶星),再从其余可见星中选3颗星和天顶星组合使其几何误差因子GDOP值最小。
3 多普勒频移计算方法
多普勒频移的计算公式为[4]:
Δfd=vscosθ·fs/c。
(11)
式中,c为光速;fs为GPS卫星的载波频率;vs为卫星的速率(3.87km/s,考虑与地球的相对运动);θ为卫星与接收机的连线和卫星速度vs的夹角。因此,由前面计算所得的卫星位置和速度可以估算出某时某颗卫星的多普勒频移。
由于GPS卫星绕地球旋转的周期为11h58min[4],与地球自转周期一同决定了每颗GPS卫星相对于地球某点的运行周期约为23h56min。所以估计GPS卫星的多普勒频移特性只需估计某地任一23h56min,该地其他时间GPS卫星的多普勒频移特性可由此推算。
4 较正方法与仿真分析
4.1 多普勒频移校正方法与仿真分析
依据上述内容,在Matlab软件环境下仿真分析了24颗卫星一周期内(23h56min)的多普勒频移变化曲线,如图3所示。

(a) 卫星1

(b) 卫星8

(c) 24颗卫星图3 绕地球一周的多普勒频移曲线(北纬30°,东经120°)
卫星不可见时,令其信号中的多普勒频移为零,图3(a)和(b)分别给出了某2颗卫星信号的多普勒频移曲线。24颗卫星相对接收机产生的多普勒频移曲线综合如图3(c)所示。
4.2 建模与多普勒频率的校正
由于卫星运行于不同的轨道上,因此,在一个运行周期内,卫星的总可见时间不同,最短的约5.3h左右,最长的需7.9h;另外,存在某些卫星,在一个周期内2次可见,单次可见的持续时间最短为2.6h左右。

任一时刻均可对应到多普勒频移周期曲线内的某一时刻te,因此,重捕时只要能够确定这一时刻te,就可通过建模估计出当前时刻下的天顶可见卫星及其多普勒频移,进而快速捕获信号。具体过程如下:
接收机首次开机后,顺序搜索12个时刻天顶可见卫星的信号,找到开机后捕获到的所有卫星,它们应该出现于某段连续时间内,覆盖12个时刻的4~5个时刻,设这5个时刻点为tj,j=i-2,…,i+2,即可确认当前时刻位于多普勒频移周期曲线中的大体时间位置为[ti-2,ti+2]。
另外,接收机首次开机后,当接收机相对地球静止且已捕获的条件下,可以由跟踪环路的NCO输出信号得到多普勒频率[3],一般可同时跟踪6~8颗卫星的信号,将这些卫星信号中的多普勒频移记录下来,在时间段[ti-2,ti+2]内,通过二分查找和比对,找到同时出现这6~8颗卫星信号的某小段时间[ta,tb]。
首次开机跟踪到信号后,每隔400s记录一次跟踪到的6~8颗卫星信号的多普勒频移,记录9点数据后,与时间段[ta,tb]内的频移曲线做比较,确定当前时刻位于如图3所示的多普勒频移周期变化曲线上的具体时刻te。由于可由跟踪环路的NCO输出得到多普勒频率,因此,可不断校正时刻te。

设得到的GPS信号多普勒频移为Δfd,则GPS接收机捕获时,载波频率的搜索以频点为(fs+Δfd)为中心展开的,伪码相位的搜索以频点为(tc+Δtd+Δfd/a)为中心展开的,其中,tc为卫星信号发射信号中的伪码相位;Δtd为GPS信号由卫星传播到接收机的传播时延引入的伪码相位变化;Δfd/a为伪码多普勒频移;a为伪码速率与载波中心频率之比。
可见,采用本文方法可有效缩小捕获搜索的空间,提高捕获速度。
多普勒频移周期变化曲线的建模:由图3可见,由卫星运动引起的多普勒频移的变化范围为±4.5kHz,随时间变化具有规律,而且具有单值性。由于具有明显的规律性,可以采用6~12个点数据的分段线性内插对多普勒频移周期变化曲线建模,其存储和计算都很简单,对捕获算法复杂度的影响可以忽略不计。具体方法为:在1周期的多普勒频移变化数据中选取6~12个取值变化最为明显的数据点,做分段线性内插,将建模结果存储起来。
当需要捕获时,访问上述模型,然后采用上述方法,参照如图4所示流程,估算多普勒频移。总估计误差一般小于500Hz。因此,可缩小搜索空间,提高捕获速度。
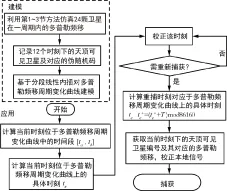
图4 多普勒频移周期变化曲线的建模及应用流程
4.3 适用性的仿真分析
下面分析卫星在一周期(23 h 56 min)内的多普勒频移情况随着接收机地理位置的不同的变化情况。经分析可知,在半径800 km左右的范围内,绝大部分时间内,同一时刻下的多普勒频移相差小于500 Hz,如图5所示。
经统计,针对卫星8信号中多普勒频移的估计,有3 500 s左右的时间内,处于不同位置点上信号中的多普勒频率的差值超过了500 Hz,期中,有1 100 s左右的时间内该差值超过了700 Hz但不到1.8 kHz;其他1.6万秒左右的可见时间段内的差值小于500 Hz。
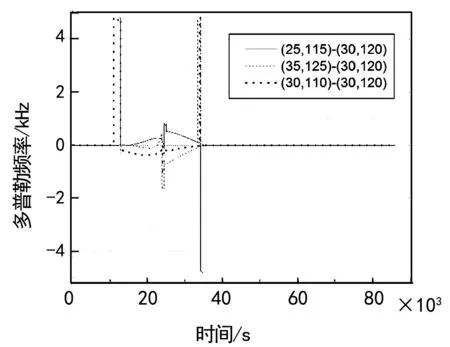
图5 某地面点800 km范围内卫星8信号中多普勒频率的差值
由图5和上述分析可知,地理位置分别在(东经115°,北纬25°)、(东经125°,北纬35°)和(东经110°,北纬30°)处的多普勒频移周期变化曲线与位置在(东经120°,北纬30°)处的多普勒频移周期变化曲线非常接近,大部分时间内它们的差别小于500 Hz。也就是说,如果接收机基于位置(东经120°,北纬30°)建模24颗卫星信号的多普勒频移周期变化曲线,利用该模型可工作于周围800 km的地区,大部分时间内由位置引入的估计误差小于500 Hz。
北纬30°,东经120°附近的城市如表1所示。由表1可见,如果GNSS接收机刚开始工作于杭州,则北至济南、西南至长沙的范围内,不用重新建模多普勒频移周期内变化的曲线,本文所述方案即可有效估算每颗卫星运动引入的多普勒频移,从而提高GPS接收机的捕获速度。

表1 北纬30°,东经120°附近的城市
由于GPS接收机时钟精度为10-6,甚至更高,因此,即使GPS接收机十几天未开机,其与卫星时钟的同步误差小于几十秒,由此引入的误差小于45 Hz。因此,应用上述模型与方法预测多普勒频移,800 km范围内的预测误差较多情况下小于500 Hz。
由于民用接收机的运动速度一般低于200 m/s(GPS卫星相对地面某点的最大运动速度可达929 m/s),因此,由接收机运动引起的GPS多普勒频移一般小于1 kHz。可见,本文所提方法可降低卫星信号捕获时的载波频率搜索范围,降低到原来的五分之一以下,因而可显著提高GPS接收机的捕获速度。
5 结束语
由于卫星绕地球的运动具有周期性,因此,当接收机相对静止的条件下,利用本文方法估计出来的多普勒曲线也具有周期性。而且多普勒随时间变化的曲线具有单值性,因此可以估计当前时刻对应在多普勒频移周期变化曲线中的具体时刻。当GPS接收机重启、或信号被遮挡导致GPS接收机失锁后重捕时,可以依据该时刻信息,利用本文方法估计载波多普勒频率并辅助接收机重新捕获。
[1] 张 蕊,黄海生.北斗卫星信号多普勒频移的电路设计[J].电子技术应用,2014,40(11):47-49.
[2] 杨 茜,秦红磊.GNSS载波多普勒频移计算、分析及实验验证[J].计算机测量与控制,2016,24(5):270-273,283.
[3] 周荣花,李昕萌,梁丹丹,等.基于变频率动态采样的导航信号高精度多普勒频移中频模拟方法[J].北京邮电大学学报,2015(2):45-49.
[4] 杨 炜.用于精确估计多普勒频移的GPS/SINS紧组合导航系统研究[D].哈尔滨:哈尔滨工程大学,2014.
[5] 李弋鹏,姜晓斐.高动态大多普勒频移伪码快速捕获技术研究[J].数字技术与应用,2015(7):81-82.
[6] ESTEVES P,SAHMOUDI M,BOUCHERET M L.Sensitivity Characterization of Differential Detectors for Acquisition of Weak GNSS Signals[J].IEEE Transactions on Aerospace & Electronic Systems,2016,52(1):20-37.
[7] KONG S.SDHT for Fast Detection of Weak GNSS Signals[J].IEEE Journal on Selected Areas in Communications,2015,33(11):1.
[8] 刘剑锋,王虹淞,李 云.卫星移动通信多普勒频移补偿研究[J].重庆邮电大学学报(自然科学版),2014,26(3):71-76.
[9] 赵 琳,高帅和,丁继成.基于FFT的高动态GPS信号捕获方法优化[J].系统工程与电子技术,2011,33(1):151-156.
[10] ZHANG A,HU F,HE Q,et al.Doppler Shift Removel Based on Instantaneous Frequency Estimation for Wayside Fault Diagnosis of Train Bearings[J].Journal of Vibration & Acoustics,2014,136(2):858-862.
[11] 袁 昱,王 钢.基于数字匹配滤波器的扩频码捕获技术研究[J].无线电通信技术,2013,39(6):86-89.
[12] ZOU X,LI W,LU B,et al.Photonic Approach to Wide-frequency-range High-resolution Microwave/millimeter-wave Doppler Frequency Shift Estimation[J].IEEE Transactions on Microwave Theory & Techniques,2015,63(4):1 421-1 430.[13] ABDELKAREEM A E,SHARIF B S,TSIMENIDIS C C.Adaptive Time Varying Doppler Shift Compensation Algorithm for OFDM-based Underwater Acoustic Communication Systems[J].Ad Hoc Networks,2015:885-891.
[14] 郑长刚,黄智刚,康成斌.导航卫星发射端多径的高精度测量技术[J].电讯技术,2016,56(2):33-38.
高法钦 男,(1974—),博士,副教授。主要研究方向:数据挖掘与大数据分析、卫星导航与基于位置的服务、软件无线电。
夏海霞 女,(1981—),博士,讲师。主要研究方向:信息与信号处理、电机内物理场的有限元分析与计算、嵌入式系统。
《无线电工程》来稿须知
1. 文章内容应具有创新性,理论科学,主题明确,层次清楚,论证严密,文字简练,数据可靠。
2. 文章应包括:中、英文标题、摘要、关键词、作者姓名、单位、城市及邮编。
3. 文章摘要字数不少于180字。摘要应包含研究目的(及主题范围)、方法、结果和结论四要素。摘要的内容应包含与论文同等量的主要信息,供读者确定有无必要阅读全文。
4. 关键词是检索的工具,是从题名、摘要和正文中选出来的能够表达文献主题的实意词和实意短语。给出术语应准确、规范、不要太偏,具有专指性和检索意义。关键词给出4~8个,用分号隔开。
5. 引言不能与摘要内容重复叙述。介绍写作背景和目的,以及相关领域内前人所做的工作和研究概况,说明本研究与前人工作的关系,目前研究的热点、存在的问题及作者工作的意义,起到定向引导的作用。引言也可点明论文的理论依据、实验基础和研究方法,简单阐述其研究内容。
6. 结束语不能与摘要、引言内容重复叙述,不能是正文中各段小结的简单重复,而是将研究过程的观察所得和实验结果等材料,经综合分析,构成若干观念和论点,并将各种数据材料联贯起来,思索判断,逻辑推理,形成最终的总体论点;所得结论应该准确、完整、明确、精炼,要认真阐述自己的创新性工作在本领域中的地位、作用以及自己新见解的意义。
7. 图表只需附必要的,随文编排,先见文字,后见图表,图表内容勿与文字表述重复。
8. 文中公式均使用公式编辑软件排版(正文中变量字符也请使用公式编辑软件排版)。
9. 参考文献之后给出所有作者简介,内容为:姓名、出生年、性别、职称或学位、专业、主要研究方向。
10. 文章最后请给出联系人的联系方式以及通信地址。
Estimation and Compensation of Doppler Shift in GNSS Signal
GAO Fa-qin,XIA Hai-xia
(SchoolofInformationScience,ZhejiangSci-TechUniversity,HangzhouZhejiang310018,China)
In order to improve the signal acquisition speed of the Global Navigation Satellite System (GNSS),a new algorithm is proposed to correct and compensate the Doppler shift in GNSS signal caused by the motion of satellites.The method of calculating satellite velocity via the dynamic equation of satellite motion,and the determination of visible satellites under the position of the GNSS receiver are discussed.Then the Doppler shift in GNSS signal introduced by satellite motion is analyzed.The curve of the Doppler shift in 24 satellite signals changing with the time is analyzed by computer simulation.Simulation results show that the Doppler shift curve varying with the time is a smooth curve with periodicity and the monodromy.And Doppler frequency shift value can be estimated just on the receiver clock.Within a range of 800 km,the estimation error is less than 500 Hz in most case.So,our new algorithm can effectively reduce the range of Doppler frequency shift and improve the acquisition speed of GNSS signal.
GNSS;Doppler shift;search range;acquisition speed
10.3969/j.issn.1003-3106.2017.04.10
高法钦,夏海霞.GNSS信号中多普勒频移的估计与补偿技术[J].无线电工程,2017,47(4):39-43,82.
2017-01-08
国家自然科学基金资助项目(61402417);浙江省自然科学基金资助项目(LY14F030025)资助。
TN967.2
A
1003-3106(2017)04-0039-05

