一道高考解析几何题带来的思考

湖北 高丰平

(作者单位：湖北省孝昌县第二高级中学)

一道高考解析几何题带来的思考

2016年的四川高考第20题(解析几何)需要学生有探究猜想的能力，先通过特殊直线将点找出来，再去证明．该道题目立足现行教材，回归数学本质，重视基础知识、基本技能的考查，强调通性通法，注重能力立意，在知识交汇处考查学生的数学思维方法和能力，同时试题在稳定中追求创新，有利于考查学生的数学素养与学习潜能，并且更注重代数与几何综合的考查．这种解题思路的变化可能对很多考生来说难以适应．该题立意深远，其本源是圆幂定理在椭圆(乃至圆锥曲线)中的推广所得到的相交弦定理、切割线定理、切线长定理等．下面就这方面的内容做几点思考与探析．

(Ⅰ)求椭圆E的方程及点T的坐标；

(Ⅱ)设O是坐标原点，直线l′平行于OT，与椭圆E交于不同的两点A,B，且与直线l交于点P．证明：存在常数λ，使得|PT|2=λ|PA|·|PB|，并求λ的值．

思考一 该题的解法多样，较为灵活，具有代表性的解法有如下几种．如图1．

【评注】 本题考查椭圆的标准方程及其几何性质，考查学生的分析问题解决问题的能力和数形结合的思想．利用解析几何中的“设而不求”法．可减少计算量，简化解题过程．

【解法二】(Ⅰ)同解法一．

【评注】该解法使用了直线的参数方程，相较于解法一运算量较小，但参数t的几何意义并不明显．下面解法三中的参数t有明确的几何意义．

【解法三】(Ⅰ)同解法一．

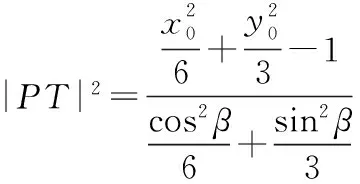
【评注】本解法中的参数t有明确的几何意义，且为数量．利用一元二次方程中根与系数的关系，得到数量之间的关系，对数据进行整体处理，避免解题过程中求根或找点的麻烦．当然直线AB与椭圆E有交点的情况下，该结论才成立．

当点A,B在椭圆E上时，该值固定，与点P的位置无关，即点P不是固定的．

思考三 更一般的情况是怎样的？

由式子结构可以联想到圆中的切割线定理，下面来做一个一般性的推导．

思考四 2016年四川卷文科20题其实考查的就是椭圆中的相交弦定理，与理科题是一对姊妹题．

(Ⅰ)求椭圆E的方程；

(作者单位：湖北省孝昌县第二高级中学)