基于单目视觉伺服系统的高速旋转球体三维速度测定

季云峰，施之皓，任杰，王朝立

基于单目视觉伺服系统的高速旋转球体三维速度测定

季云峰1，施之皓1，任杰1，王朝立2

单目视觉所处理的信息是目标物体在三维空间内的信息向二维平面的投影，故还原目标的深度信息，对于预测目标轨迹和后续控制决策具有重要的意义。提出一种基于单目视觉的高速旋转球体三维速度的方向及大小的测定算法，利用球体上单个标记的运动轨迹来识别球体旋转速度及旋转轴的方向。摄像机角度固定，当球体旋转轴正对摄像机时，球体标记运动形成的运动轨迹是一个圆，而当球体旋转轴方向发生改变时，球体标记运动轨迹将会变成一个椭圆，不同的方向形成椭圆的长短轴不一样，利用这个特征来计算旋转轴的方向。该算法可用于测量乒乓球旋转中，旨在应用于乒乓球机器人的视觉识别，对机器人后续阶段的运动规划和控制决策起到重要的作用。对所提算法进行了实验验证，得到与理论结果误差较小的实验数据，验证了方法的可行性。

单目视觉；旋转球体；三维速度

1 引言

利用摄像机等视觉传感器获取自然空间中目标图像序列，分析目标物体的特征，解析目标与摄像机之间的几何关系，定位目标空间位置和姿态，从而实现对目标物体的运动估计与分析，这是计算机视觉领域一个古老但也十分重要的研究课题，具有非常广泛的应用背景。现有的目标定位方法主要分为单目视觉、双目立体视觉和多目立体视觉。立体视觉是基于立体视差的原理，利用有差异的图像产生深度感，通过双目摄像机及目标物体的几何关系，得到视场内目标的运动及姿态的变化参数［1］。故传统意义上要得到目标的三维信息，需要双目或者多目摄像机的空间配合拍摄才能完成。但在现实测量过程中，出于精简成本，减小计算量，缩短计算时间等多方面原因考虑，基于单目摄像机来对目标进行空间测定具有较大的实用价值。

单目摄像机从理论上来说只能拍摄到目标物体的二维信息，即某一个平面上的信息，所以需要利用目标的相关运动特征及信息。Nakashina提出了一种单目视觉测量的新方法，其原理是利用物体的已知运动和采集到的前后两幅图像比例的变化得出镜头与目标的距离［10］。有研究者对不同纹理下的目标物体进行测量，显示了算法在不同纹理下具有良好的性能［5，13］。在此基础上，Ashutash等［6］利用多幅图像建立的模型对深度信息进行了预测。

大部分基于单目视觉做的研究基本应用于直线测距、机器人定位导航、机器人零部件精加工，而应用在球体旋转测速中的基本没有。基于球体测速最常见的应用在乒乓球机器人中，旋转是乒乓球一个很重要的信息，机器人想要很精准的击打乒乓球，必须要对乒乓球的旋转进行判断。Nakashima等［11，12］在球上做标记，通过高速视觉来对球的旋转进行测算。除了用标记来测旋转之外，还可以通过对乒乓球运动轨迹的分析来推测出旋转。Matsushima等［9］利用经验学习的方法，主要采用了局部加权回归法（LWR）来进行轨迹预测，并获得旋转信息。Yanlong等［15-17］通过对乒乓球进行受力分析，建立参数模型，通过迭代来预测飞行轨迹，预测信息中包含模糊的旋转信息。

目前，尚未提出一个精确的不做标记的方法来对球体旋转的三维速度进行测量。本文主要针对球体旋转速度大小及方向问题，利用球体旋转中的一些特征，提出一种基于单目摄像机的测量球体三维速度的方法，并用实验验证了算法的有效性。在实际应用中，需要摄像机拍摄到球体上的标注关键点，球体上的商标，若只用1台摄像机的话确实会遇到一些拍不到商标的情况，所以，在实际应用中一般摆放2台摄像机，如乒乓球视觉系统中，将摄像机摆放在乒乓球台的两边，同时对乒乓球进行检测，一般情况下，总会有1台摄像机拍摄到乒乓球的商标，用拍摄到商标的这个摄像机作为计算球速的切入口，用这种方法就可以测算出乒乓球的转速。

2 球体旋转速度测定

2.1 球体旋转模型

在本文中，需要基于单目摄像机来对旋转球体进行拍摄，利用旋转球体的旋转特征来计算球体的旋转速度的大小和方向。先对旋转球体的特征进行分析（图1）。

在空间坐标系o-xyz中，2个黑色圆代表1个球体，其中，实线圆代表球体投影在x-o-y平面形成的圆，虚线圆代表球体上任意一个截面所形成的圆。2个红色方框代表2个圆形所在的截面，已知在空间中2个平面相交会产生1条交线，在图1中2个平面相交的交线即为中间那条黑色直线。而这2个圆形截面的交线，即为虚线圆的直径，记为直径m，属于2个平面交线的一部分。

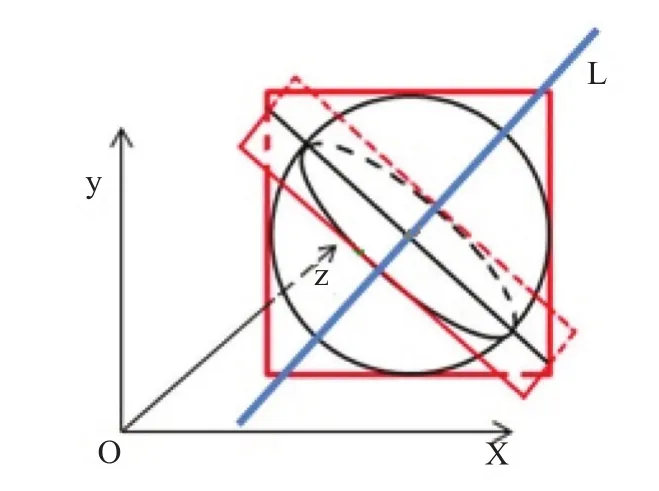
图1 球体旋转模型Figure 1.The Model of Sphere Rotation

2.2 球体三维速度分解

高速旋转的球体必将沿着某条通过球心的轴进行转动，故可将求解高速旋转球体的三维速度方向问题转化为求解转动轴空间位置问题。现假设此球体旋转方向为沿着虚线圆旋转，则此球体的转动轴为垂直于虚线圆所在截面的直径m的中垂线所在直线，即为直线L（图2）。

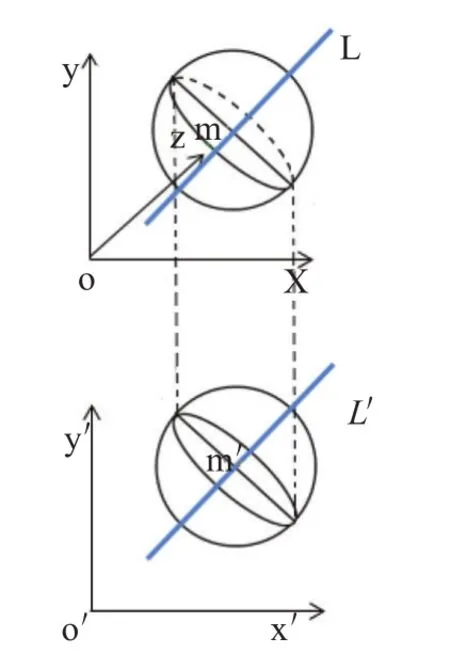
图2 球体三维速度分解Figure 2.Decomposition of Three Dimensional Velocity of the Sphere

如图2所示，将高速旋转球体投影到x-o-y平面上，可以得到球体在新的坐标系x′-o′-y′的平面图形。此时，空间坐标中的实线圆保持不变，而空间坐标中的虚线圆将在平面中被投影成1个椭圆。此外，空间中的转动轴L将被投影到平面x′-o′-y′中，成为椭圆长轴m′的中垂线L′。

故可将求解旋转球体转动轴L空间位置问题转化为两个问题：1）直线L′在平面x′-o′-y′位置；2）直线L′与平面x′-o′-y′夹角。

2.3 求解旋转轴方向

2.3.1 直线L′在平面x′-o′-y′位置

先解决直线L′在平面x′-o′-y′位置问题，可转化为求解椭圆长轴m′与x轴倾角及椭圆中心点坐标问题。对于任意一个椭圆，都可以用其一般方程Ax2+Bxy+Cy2+Dx+Ey+1=0表示，总共有A、B、C、D、E5个系数，即只要找到椭圆上面任何5个点的坐标就可以解出椭圆的一般方程。例如，在乒乓球旋转测定中，可以利用乒乓球上面的商标中心来作为识别对象，记下5帧图像中商标中心位置即可。假设找到椭圆上任意5个点的坐标为（xn，yn），n=1，2，3，4，5，则可以得到以下五元一次方程组：

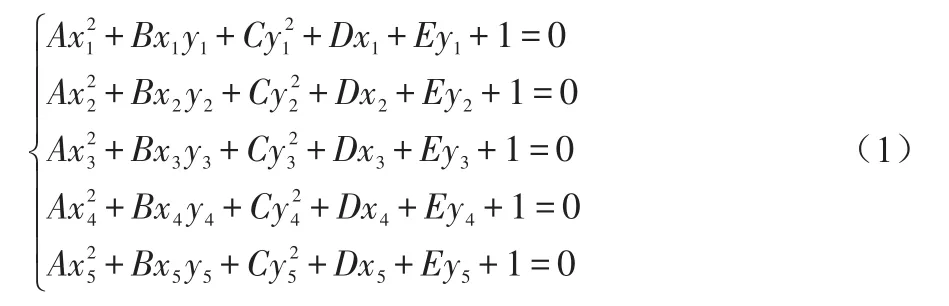
再利用matlab软件编程求解方程（1）的解，获得系数值，从而得到椭圆一般方程之后，开始计算椭圆长轴与x轴倾角及椭圆中心点坐标。令：

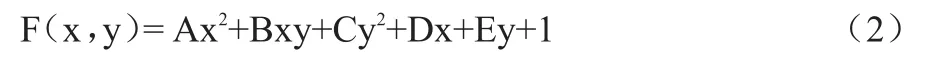
由于椭圆属于中心型曲线，则中心点坐标（x0，y0）满足

代入F（x，y）有

解方程组可得

即得椭圆中心坐标为（x0，y0）。

假设椭圆长轴m′与x轴倾角为β，现将原坐标系沿着x轴旋转β角，令坐标系中任意一点坐标为（x1，y1），其对应于新坐标系的坐标为（x′1，y′1），根据解析几何中相关变换，可以得到如下关系：

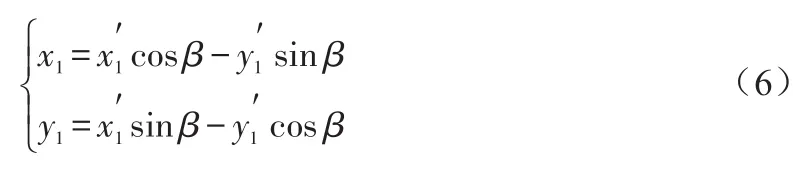
令F（x）=0，将（6）式代入，可得：

其中，

要求夹角β，即将坐标轴旋转β角度，此时x′1y′1的系数B′值为0，即：

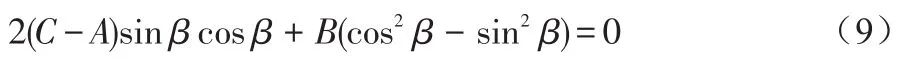
利用二倍角公式：

化简得：

即可得到椭圆长轴m′与x轴倾角β的值为：

2.3.2 直线L′与平面x′-o′-y′夹角

接下来解决直线L′与平面x′-o′-y′夹角，在单目摄像机视角下，一个与摄像机视角平面倾角为α的平面中的1个圆会被识别成1个椭圆。其主要原因是将原本平面中圆投射到摄像机视角平面中，从而导致图像变形，椭圆的短轴就是因为原本直径投射到新平面下缩短所形成的。

如图3所示，假设摄像机视角平面为x1-o-y1平面，则计算机视角平面与圆所在平面的夹角为α，投影形成的三角形的3条边长分别为a、b、c，原本圆的直径为c，投影到x1-o-y1平面上变成椭圆短轴b，则有：

而此处的夹角α即为直线L′与平面x′-o′-y′夹角，三角形的边长b和c即为椭圆的长轴和短轴，记椭圆长轴为a′，短轴为b′，可得：

故可将问题转化为求解椭圆长轴和短轴问题。根据前文计算结果，可知椭圆中心坐标为（x0，y0），假设一条直线过椭圆中心点与x轴夹角为ϕ，则这条直线的参数方程为：

其中，t为参数，ϕ为直线与x轴夹角。

令F（x）=0，将（15）式代入，可得：

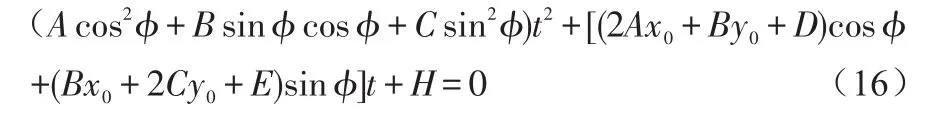
其中，

将前文算出的中心坐标值代入式（17），可得：

假设根据式（16）求解得方程的两根为t1,t2，由参数|t|的几何意义可知，经过对称中心点(x0,y0)的弦的长度为：

由式（23）可求得倾角为ϕ的以(x0,y0)为中点的弦的长度，因为椭圆的长轴、短轴分别是其弦中最长和最短的2根弦，当 Acos2ϕ+Bsinϕcosϕ+Csin2取得极值的时候，对应的弦即为椭圆的长轴和短轴。

令G=Acos2ϕ+Bsinϕcosϕ+Csin2，则：

故可求得椭圆的长轴a＇和短轴b＇长度如下：

根据式（14）（18）（28）可得直线L′与平面x′-o′-y′夹角α的计算公式：

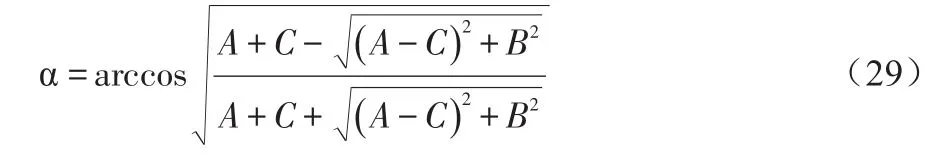
2.4 求解旋转速度大小

至此，已解决球体旋转方向问题，接下来考虑球体转速问题。精确的计算速度大小的方法是先计算任意两帧图像中同一点运动的弧线的距离，然后除以两帧图像相隔时间，即得到球体转速大小。但其计算量会相对较大，在高速旋转球体上，可以将两点之间的弧线距离近似为两点之间的直线距离，从而可以大幅度降低计算量，缩短计算时间。本文选取了椭圆上的5个点，即同一个点连续5帧的运动轨迹，为了降低误差，将选取这5点中每相邻2点之间距离的平均值。根据前文可知，椭圆上任意5个点的坐标为（xn，yn），n=1，2，3，4，5，记球体旋转速度大小为v，每2帧之间间隔时间为t，物体实际大小与图像中像素大小比值为k，则有

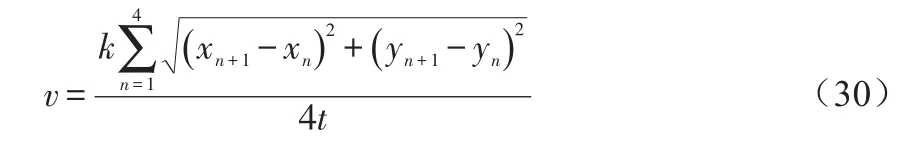
公式（30）可以计算出的v为选取坐标点的线速度，可以根据线速度v计算球体旋转的角速度。球体是绕旋转轴进行旋转的，本文所选取的点的运动轨迹是垂直于旋转轴的一个圆，但是，这个圆不一定会经过球心，所以不能简单的利用球体的半径来计算角速度。本文计算角速度应该利用所选取点运动轨迹圆的半径，而在单目视觉中，这个半径即为椭圆轨迹的长轴a＇。故利用公式（28）和公式（30）可算得球体旋转的角速度计算公式：

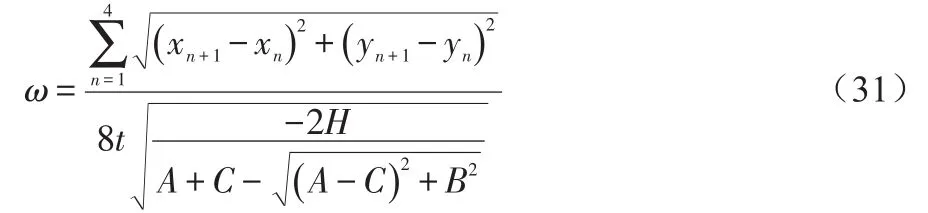
3 实验验证及分析

3.1 实验验证

为了验证该设计算法的正确性，本文自制了一个旋转测速仪器，该仪器可以直接测量转速，再利用设计的算法计算转速，进行实验对照，仪器如图4所示。

图4 旋转测速仪器Figure 4.The Rotating Speed Measuring Instrument

该旋转测速仪器主要由以下几部分构成：24 V稳压电源，高速无刷伺服电机，控制器，脉冲发射器，液晶显示屏1，液晶显示屏2。主要工作原理为：24 V稳压电源供电，利用脉冲发射器发射脉冲，通过控制器传给高速无刷伺服电机，使电机转动，电机转动的速度大小与脉冲发射的频率相关，液晶显示屏1显示的是脉冲发射的频率，即每秒发射的脉冲数，液晶显示屏2显示的是球体的转速大小，单位为r/min，即每分钟球体旋转的圈数。

本文选用的高速无刷伺服电机的转动速度与发射脉冲频率相关，每发射一个脉冲电机转动0.36°，即每发射1 000个脉冲电机旋转1周，故液晶显示屏1和液晶显示屏2上显示的数字有相对应关系。设脉冲发射器每秒发射的脉冲数为M，球体的旋转速度为N，其中，M和N为液晶显示屏1和液晶显示屏2上显示的数字，可得到相对应关系如下：

化简可得：

本文所采用的电机控制精确，精度很高，该电机的转速范围为0～1800 r/min，即最快可以达到30 r/s，为进一步提高精度，本文采用最大量程的一半转速，即900 r/min来进行实验验证，实验结果为：M=14 897，N=901.1，满足公式（33）。

本文将一个白色塑料球放到自制旋转测速仪上，采用高速摄像机利用50帧/s的速度进行拍摄，球体上有一处标记，用kinovea软件来获取点的坐标，再根据模型来验证，逐帧获取球体上同一点的5个坐标，为了简化球体模型，尽量将平面坐标系中心选取在轴上。

选取的5个坐标分别为：（75，-27），（36，-63），（1，-70），（-34，-64），（-71，-30），代入椭圆一般方程，用matlab计算可得：

利用上面夹角模型可以计算出2个夹角分别为：

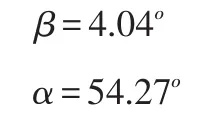
由于选择坐标系中心点尽量靠近坐标轴，故理想中的β值为0ο，测量中可能会由于中心不准有一定误差，在可接受范围内。

根据实际测量数据，摄像机镜头中心离地面距离为123.8 cm，球体中心离地面80.5 cm，镜头中心离球体中心距离为54.8 cm，根据实际数据可测得摄像机拍摄平面与球体平面夹角α计算公式：

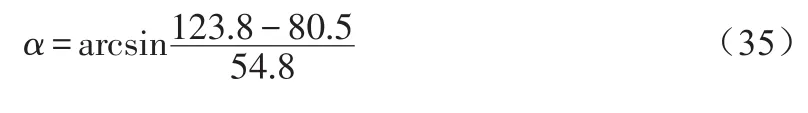
可计算出：

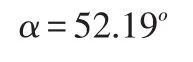
与实际计算结果误差不大，在可接受范围之内。

再利用上面角速度模型可以计算出角速度为：

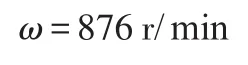
角速度与实际测量角速度之间的误差为：

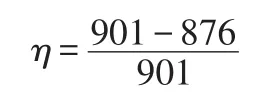
计算可得误差为：

角速度计算误差控制在2.77%，基本可以验证本算法的正确性。至此，在误差允许的范围内，已用对照实验验证了本算法的正确性。

3.2 不同转速下的误差分析

上面已经用实验证明了在15 r/s，即900 r/min的转速下的算法的正确性，接下来将针对不同转速下的情况来利用算法进行实验验证。由于制作的旋转测速仪器中的伺服电机最高转速为30 r/s，所以将5转作为间隔，分别计算5 r/s、10 r/s、15 r/s、20 r/s、25 r/s、30 r/s这6种旋转速度下算法的正确性，并对误差进行分析。由于测速仪的单位是r/min，故将每秒的转速转换为每分钟的转速，即300 r/min、600 r/min、900 r/min、1 200 r/min、1 500 r/min、1 800 r/min，分别利用算法进行实验，并计算误差，实验结果如表1所示。

表1 不同转速下的实验结果Table 1 The Experimental Results of Different Rotational Speeds

根据表1所得的计算结果，将不同转速下的误差用matlab画出坐标系，其中，横坐标代表的是球的转速，从300～1 800，单位是r/min，纵坐标代表的实验误差，从2～4，单位是%，如图5所示。

由表1和图5可以发现，本文算法的实验误差基本可以控制在4%以内，并且随着转速的升高误差呈降低趋势，造成这种原因可能是由于随着转速的升高，基数增大，那些由于环境光照及摄像畸变造成的误差相应减小，从而使得计算误差降低，这也在一定程度上验证了本文算法的正确性。

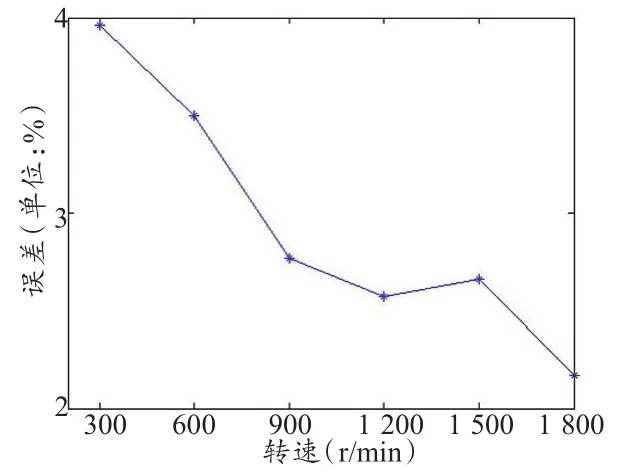
图5 不同转速下的误差结果Figure 5. Error Results of Different Rotational Speeds

4 扩展

之前的方法可以适用于在椭圆轨迹上任意找5个点来进行推算，在乒乓球运动过程中，由于速度很快，受到阻力相对较小，所以，在短时间内的旋转速度可以被视为匀速。以乒乓球作为参照物，在以转动轴为中心旋转时，球上某一个固定点将会绕着转动轴做近似匀速圆周运动。假设高速摄像机的帧数足够大，可以拍到球上固定点连续5帧相对于乒乓球的坐标位置，则这5个坐标将满足在圆上相对距离相等的特征。故这个特征可以作为识别的一个条件，从而减少需要识别的坐标点数目，将5个坐标缩减为4个坐标。通过前3个坐标中相邻坐标距离相等来建立椭圆方程系数之间的关系，加上4个坐标分别代入方程形成方程组，从而求解系数，获得椭圆一般方程，再根据之前的算法来进行乒乓球运动速度及方向的计算。

由于高速摄像机获得的4个点的坐标是椭圆上的，故需要先将椭圆上的坐标转换为圆上面的坐标，再根据相邻坐标距离相等来建立第5个方程。

先来找关于椭圆和圆之间的关系，根据前文，椭圆是对应的圆通过一定角度投影形成的，故它们之间满足一定联系。将此椭圆和圆的中心重叠，并以此中心作为原点建立坐标系，如图6所示。

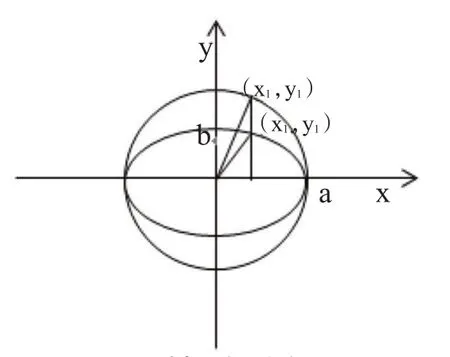
图6 椭圆与对应圆Figure 6.The Ellipse and Corresponding Circle

在摄像机拍摄过程中，图像中选择的坐标系原点一般不会与球运动轨迹形成椭圆的中心重合，故需要将图像中检测的坐标转为以椭圆中心为原点的坐标，再进行后续计算。假设图像坐标系为O-uv，将椭圆坐标系代入图像坐标系中，如图7所示。

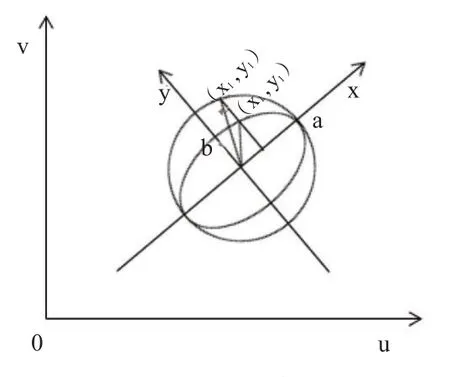
图7 坐标系转换Figure 7.Coordinate System Transition

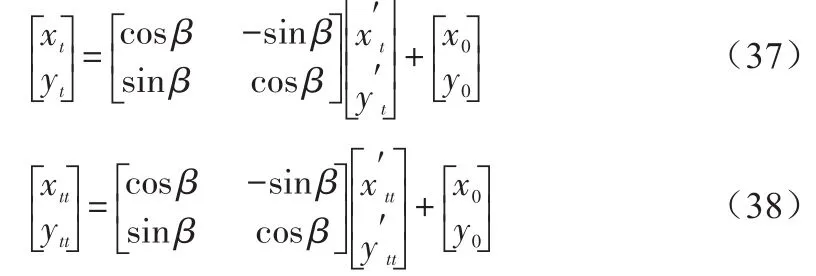
高速摄像机拍到图像，可以检测到乒乓球商标在图像坐标系中的坐标，即，连续拍到4帧图像，即可以找到4个点坐标，可形成一个椭圆的轨迹，带入式（39）可得到对应的圆的方程，再根据圆上4个点连续2点距离相等来建立方程，加上4个坐标分别代入方程形成方程组，从而求解系数，获得椭圆一般方程。结合公式（12）和公式（29）可以将公式（39）转化为只含系数的公式：

假设高速摄像机拍摄到乒乓球连续4帧的商标在乒乓球上的坐标依次为（xn，yn），n=1，2，3，4，代入公式（40），计算出对应的圆上面的坐标，n=1，2，3，4，再根据相邻点距离相等建立公式：

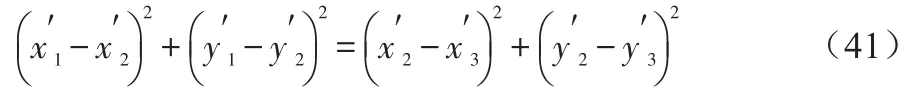
再将4个点代入椭圆一般方程形成4个方程：

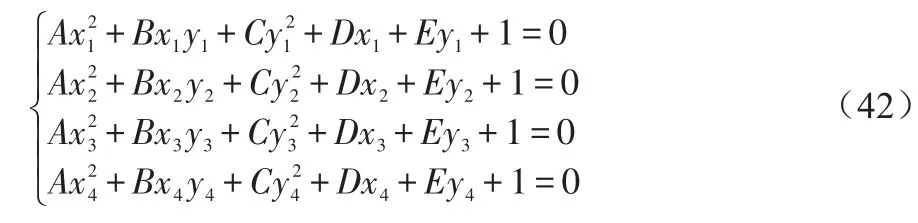
结合公式（40）、（41）、（42）建立方程组，由于含二次项，故解可能不唯一，再利用另外3个相邻点距离相等来对结果进行取舍，公式如下所示：

至此，完成用4个相等距离点完成检测任务。

实验验证跟之前的实验类似，找到4个连续的点坐标代入公式计算即可，此处不再赘述。

5 结论及建议

本研究提出了一种基于单目视觉的识别球体旋转三维速度及大小的算法，利用球体上任何一处特征点标记在高速摄像机中5或4帧图像的位置坐标来建立旋转参数方程，最后根据旋转特征信息来获得球体旋转的三维速度及大小，并用实验验证了算法的有效性。目前，该算法主要应用于乒乓球轨迹识别及预测中，在保证识别精度的情况下，对于乒乓球机器人后续阶段的运动规划和动作决策起着重要的作用，这个接下来也作为笔者所努力的方向。希望在今后的应用识别中，提高图像识别的精度，将算法更加有效地应用于乒乓球机器人中，从而完成准确击打的任务。

［1］孔令富，刘巧娜，赵立强.基于单目运动摄像机的三维物体运动参数估计［J］.燕山大学学报，2012，36（4）:310-315.

［2］吕林根.解析几何［M］.北京：高等教育出版社，1986.

［3］芮庆，胡宗武，宫崎文夫.用LWR学习进行乒乓球轨道预测的仿真研究［J］.机器人，1998，20（5）:373-377.

［4］任艳青，方灶军，徐德，等.基于模糊神经网络的乒乓球旋转飞行轨迹模式分类［J］.控制与决策，2014，29（2）:263-269.

［5］石春琴，张丽艳，韦虎，等.随机模式投影双目测量系统中的单目测量［J］.光学精密工程，2010，18（1）:257-264.

［6］ASHUTOSH S，SUNG H，ADDREW Y.Learning depth from single monocular images［J］.Adv Neural Inform Process Syst，2005，18:1161-1168.

［7］LIU C，HAYAKAWA Y，NAKASHIMA A.A registration algorithm for on-line measuring the rotational velocity of a table tennis ball.in Proceeding of IEEE/RS［J］.Int Conf Intelligent Robots Syst，2011:2270-2275.

［8］LEUNG H，WANG H，CAO C.An improved locally weighted regression for a converter re-vanadium prediction modeling［C］// The 6th World Congress on Intelligent Control and Automation. Dalian，2006:151-1519.

［9］MATSUSHIMA M，HASHIMOTO T，TAKEUCHI M.A learning approach to robotic table tennis［J］.IEEE Trans Robot，2005，21（4）:767-771.

［10］NAKASHIMA A，OGAWA Y.Robotic table tennis based on physical models of aerodynamics and rebounds［C］//Conference:Robotics and Biomimetics（ROBIO），IEEE International Conference，2011:2348-2354.

［11］NAKASHIMAA，OGAWAY，CHUNFANG L，et al.A real-time measuring method of translational/rotational velocity of a table tennis ball［C］//Proceeding of 5th IFAC Symposium on Mechatronic Systems，2010:732-738.

［12］SUN L，LIU J，WANG Y.Ball’s flight trajectory prediction for table-tennis game by humanoid robot［C］//IEEE Int Conf on Robotics and Biomimetics.Guilin，2009:1136-1141.

［13］WANG G，WANG C，CAI X，et al.Distributed adaptive output consensus tracking of higher-order systems with unknown control directions［J］.Neurocomputing，2016，203:129-138.

［14］XIAOPENG C，YE T，QIANG H.Dynamic model based ball trajectory prediction for a robot ping-pong player［C］//The 2010 IEEE Int Conf on Robotics and Biomimetics.Tianjin，2010:603-608.

［15］YANLONG H，DE X，MIN T.Trajectory prediction of spinning ball for ping-pong player robot［C］//2011 IEEE/RSJ Int Conf on Intelligent Robots and Systems.San Francisco，2011:3434-3439.

［16］YAMAGUTI N，SHUNICHIRO O，TERADA K.Method of distance measurement by using monocular camera［C］//SICE 97. Proceedings of the 36th SICE Annual Conference.International Session Papers，1997:1255-1260.

［17］YAMAGUTI N，SHUNICHIRO O，TERADA K.A distance measurement method available to texture surface by using Complex-Log Mapping［C］//Industrial Electronics，Control and Instramentation，1997，IECON 97.23rd International Conference，2006: 1142-1147.

3D Velocity Measurement of High-speed Rotating Sphere based on the Monocular Vision Servo System

JI Yun-feng1，SHI Zhi-hao1，REN Jie1，WANG Chao-li2

The information monocular visual processed is a target object that project from 3D to 2D. So restoring the depth information is very important to the prediction of target trajectory and subsequent control decision.This paper presents an algorithm based on monocular vision that can calculate 3D velocity of high-speed rotating sphere.The algorithm mainly uses the single trajectory on the sphere to identify the rotation speed of the sphere and the direction of the rotation axis.The angle of the camera is fixed，and when the sphere rotates on the camera，the moving track formed by the ball mark motion is a circle.When the direction of the axis of rotation of the sphere is changed，the trajectory of the mark on the ball will become an ellipse.When the direction of the rotation axis is different，the shape of ellipse becomes different.This algorithm can be used to calculate the rotating velocity of table tennis ball.The algorithm will be applied to vision recognition of table tennis robot，which play an important role in motion planning and control decision of robot.The experimental results of the proposed algorithm are verified with little error，which proves the feasibility of the proposed method.

monocular visual；rotating sphere；3D velocity

1002-9826（2017）02-0139-07

10.16470/j.csst.201702019

G846

：A

2016-06-01；

：2016-12-27

上海市科学技术委员会科研计划项目（15490503100）；国家体育总局科研课题（2014B072）；上海体育学院研究生教育创新基金（yjscx2016007）。

季云峰，男，在读博士研究生，主要研究方向为机器视觉，E-mail：ji_yunfeng2015@163.com。

施之皓，男，教授，博士，博士研究生导师，主要研究方向为运动训练学，E-mail：shizhcttc@163.com。

1.上海体育学院中国乒乓球学院，上海 200438；2.上海理工大学光电信息与计算机工程学院，上海 200093

1.Shanghai University of Sport，Shanghai 200438，China；2.University of Shanghai for Science and Technology，Shanghai 200093，China.