sEMG时频特征线性回归法与非线性神经网络法预测伸膝肌群极限功率保持能力测试中功率损失率的比较研究

徐红旗，史冀鹏，张守伟，徐欣，杨传崎，杨帆，张欣，赵朝义

sEMG时频特征线性回归法与非线性神经网络法预测伸膝肌群极限功率保持能力测试中功率损失率的比较研究

徐红旗1，史冀鹏1，张守伟1，徐欣1，杨传崎2，杨帆3，张欣4，赵朝义4

目的：拟比较sEMG时频特征线性回归法与非线性神经网络法预测伸膝肌群极限功率保持能力测试中功率损失率的差异。方法：BTE PrimusRS系统与肌电仪同步，40名男大学生膝关节重复性屈伸运动至疲劳，阻力设置50%等长峰值力矩，动作频率60次/min。求取每次伸膝阶段极限功率损失率（Power%），伸膝肌群sEMG时域（MAV%、RMS%）、频域（MNF%、MDF%）与瞬时频率（IMNF%、IMDF%）参数变化率，基于sEMG时频特征参数（MAV、ZC、SSC、WL）建立多层感知人工神经网络模型，求取功率真实值与估计值。结果：IMDF%能单独解释股内肌、股直肌与股外肌极限功率损失率的方差变异为6.33%、22.71%、12.31%，IMDF%联合其他时频参数一起能解释的方差变异为6.95%、25.93%和16.05%，非线性神经网络法求取的功率估计值能解释的方差变异为10.43%、34.23%和18.05%，且信噪比值逐步增大。线性与非线性技术功率真实值与估计值拟合所得两直线的斜率与截距有显著性差异（P＜0.05）。结论：sEMG时频特征线性回归法与非线性神经网络法，均能很好地追踪人体神经肌肉系统动态工作疲劳过程中输出功率的损失，但后者的准确性要优于前者。

极限功率；表面肌电；小波变换；瞬时频率；人工神经网络

1 引言

体育运动、日常生活活动及工农业生产劳动等均是在人体中枢神经系统的支配下，肌肉收缩产生动力，牵拉骨杠杆以关节为枢纽进行转动，进而实现的一种动态做功过程。神经肌肉系统动态功率发展与保持能力的研究在体育科学、康复医学、人机工效学、航空医学等领域均具有重要的意义。功率的物理学定义是单位时间内的能量输出或是工作的速率。在人体转动力学中，肌肉功率为运动环节角速度与扭矩的乘积［37］，因此，无论速度的快慢，均会有功率的输出且可被测量。人类日常活动动作中，运动环节会由等长收缩的静止阶段，过渡到克服阻力后的加速阶段，再到关节终止位前的保护性减速阶段，环节运动角速度整体上呈冲击正弦曲线式变化，肌肉最大功率仅在肌力适中时的收缩速度下出现。在旋转式测力系统中，扭矩、速度与功率三者间的关系表明，肌肉极限功率出现在阻力矩值与角速度值均接近其最大值的50%时［2］。通过测量人体完成特定任务时的总功输出量或是持续一项活动的时间长度，可以直接量化特定肌群功率的保持能力［2］。神经肌肉系统机械输出功率的变化与肌肉的疲劳现象密切相关，在肌肉动态功率测试中同步采集做功肌群的表面肌电（Surface Electromyography，sEMG）数据，可以监测肌肉动态工作疲劳过程中输出功率的变化特征，分析肌肉活动的神经控制机制与肌肉的功能状态［19］，明确神经肌肉系统功率保持能力的影响因素与变化特征。

伴随着每次sEMG信号的触发，肌肉功率的输出，肌纤维长度与收缩速度，被激活肌纤维与表面电极之间的位置均会发生变化。因此，神经肌肉系统动态工作中记录的sEMG信号具有不平稳性。时频分析法是分析非平稳信号的有力工具，Karlsson等［26］比较了如短时傅立叶变换（Short Time Fourier Transform，STFT）、维格纳分布（Wigner Distribution，WD）、乔伊-威廉斯分布（Choi-Williams Distribution，CWD）与连续型小波变换（Continuous Wavelet Transform，CWT）等不同时频分析法后发现，CWT法较其他时频分析法具有更好的准确度与评价能力。考虑到动态sEMG信号既具非平稳性又具非线性的特点，基于一个能鉴别非线性关系的神经网络（Neural Network，NN）学习程序建立起非线性模型，Maclsaac等［30］应用人工神经网络联合sEMG信号的不同时间与频率特征形成一个肌肉疲劳监测指标，与单独应用平均频率（Mean Frequency，MNF）或瞬时平均频率（Instantaneous Mean Frequency，IMNF）相比，能较为准确地跟踪肌肉疲劳时的sEMG变化特征。与线性预测模型相比，非线性分析法的学习程序计算量大，并且费时长［19］，基于常规sEMG时频参数的线性回归法在用于监测神经肌肉系统动态工作疲劳中输出功率的变化特征时，是否能达到既保证预测精度又减少计算工作量的效果［2］，需要直接比较线性与非线性两法预测神经肌肉系统动态工作疲劳中机械输出功率损失率的差异，然而此方面的研究较少［21］。

本研究拟在对青年人伸膝肌群极限功率保持能力进行测试的同时，同步记录运动环节转动的角度、角速度与扭矩等参数以及伸膝肌群的sEMG数据。采用线性CWT时频分析与非线性多层感知人工神经网络（Multi-Layer Perception Neural Network，MLPNN）模型法分析sEMG数据，以比较时频参数线性回归法与非线性NN法预测神经肌肉系统机械输出功率损失率的差异，为建立一套行之有效的神经肌肉功能电生理评价方法提供理论依据，为人体单关节肌群动态做功能力的测评积累基础数据。

2 研究对象与方法

2.1 研究对象

健康普通男大学生，年龄21.22±1.10岁，身高173.81± 3.44 cm、体重65.29±6.49 kg、BMI 21.61±2.09 kg/m2。以身高、体重2个项目为基础数据，据2005年《第二次国民体质监测报告》中20～25岁年龄段全国成年男性身高（170.4± 6.23 cm，n=10 344）与体重（63.7±10.50 kg，n=10 340）的二维分布概率，在相应的身高、体重范围内选定相应比例的人数，组成本研究40人的样本量。经单一总体均数t检验（One-Sample T Test）可知，所选样本的身高、体重、BMI与全国20～25岁成年男性无显著性差异（P＞0.05）。

2.2 研究方法

2.2.1 准备阶段

自行编制的《受试者调查问卷》由测试者负责讲解与指导填写，并回收与检查，以获取受试者的基本信息与健康状况，排除疾患以确保安全。受试者穿着短裤、背心，由测试者进行基本形态指标的测量，每个指标测试2次。使用一次性Ag-AgCl电极片，在粘贴电极片前，用去毛刀去除粘贴处体毛，以75%乙醇擦拭皮肤以降低阻抗。电极粘贴处为右下肢股内侧肌、股直肌与股外侧肌。以下肢活动为主，准备活动的量与强度以全身发热，不感到疲劳为宜；准备活动后心率约为100～120次/min。

2.2.2 伸膝肌群极限功率保持能力测试阶段

测试仪器：BTE PrimusRS模拟仿真测试评价训练系统（Baltimore Therapeutic Equipment，BTE）与Noraxon表面肌电仪同步。

测试姿势：要求受试者取坐姿，双臂交叉放于胸前，膝关节转动中心与系统测试头转轴保持同一直线，以大小腿伸直位为180°，在90°ROM范围屈伸，大腿与躯干用绑带固定（图1）。

测试步骤：首先，在大小腿屈曲110°时进行伸膝肌群等长峰值力矩（The Isometric Peak Torque，IPT）测试，重复测试3次，测试时间3 s，组间间歇5 s，采用非爆发式静力性测量模式，组内变异系数（Coefficient of Variation，CV）控制在10%以内。其次，进行伸膝肌群极限功率保持能力测试（The Retentive Capacity of Muscular Peak Power），采用向心/离心模式，阻力设置50%IPT，运动幅度（90°ROM）与动作频率一定，测试频率60次/min，持续运动直至疲劳。

2.2.3 数据的采集与处理

BTE PrimusRS系统自动记录3次等长峰值力矩，1次极限功率保持能力的总功（J）、距离（deg）与时间（s）。BTE PrimusRS系统工作头转动的时间（Time）、角度（Angle）、角速度（Angular Velocity）与扭矩（Torque）参数，功率（Power）为角速度与扭矩的乘积，以及3块肌肉的sEMG数据，均由Noraxon肌电仪同步记录。采样频率1 500 Hz，以“.TXT”格式导出并保存，预处理后导入MatlabR2014a软件，经自行编制的数据库运算程序处理，主要步骤：

2.2.3.1 动作划分依据

由伸膝肌群极限功率保持能力测试中角度、角速度、扭矩与功率随时间的变化规律可知（图2），当角度在0°附近时，肌力矩小于阻力矩（50%IPT），伸膝肌群做等长收缩；当肌力矩大于阻力矩（50%IPT）时，运动环节进行爆发冲击式向心收缩，角速度与功率成正弦曲线式变化，直至接近大小腿伸直位，且功率与角速度峰值在此阶段出现；随后，伸膝肌群离心收缩，运动环节开始回位。因此，以“角速度”大于“0”对应的起止时间点作为动作划分的依据。

2.2.3.2 伸膝肌群极限功率损失率与线性时频参数的提取

对BTE PrimusRS系统工作头转动的角度、角速度、扭矩、功率等数据采用相邻平均法（Adjacent Averaging）平滑处理后，以“角速度”大于“0”对应的起止时间点截取相对的角度、扭矩、功率与sEMG数据。求取每一段角度、角速度、扭矩与功率的峰值（Max），sEMG数据时域参数平均绝对值（Mean absolute value，MAV）与均方根值（Root mean square，RMS），基于快速傅立叶变换法（Fast Fourier Transformation，FFT）获取频域参数平均频率（Mean Frequency，MNF）与中位频率（Median Frequency，MDF）［12，19］。连续性小波变换法以Harr小波（DB1小波）为母小波，采用小波变换将sEMG数据分解为6层；保留近似尺度上的小波系数，去除高频细节上的小波系数，以去除杂点；应用保留的小波系数重构信号，完成小波变换后的去噪过程［3，12］；运用希尔伯特变换（Hilbert Transform），求取sEMG数据的瞬时平均频率（Instantaneous Mean Frequency，IMNF）与瞬时中位频率（Instantaneous Median Frequency，IMDF）［12，38，41］。

本研究以前2次伸膝动作的极限功率与时频参数均值为基准值，除以前2次均值以求取极限功率损失率（Power%）与时频参数变化率（MAV%、RMS%、MNF%、MDF%、IMNF%、IMDF%），通过比较极限功率损失率与时频参数变化率之间相关关系的强弱，来明确不同电生理学法（sEMG时频特征线性回归法与非线性神经网络法）的性能优劣。

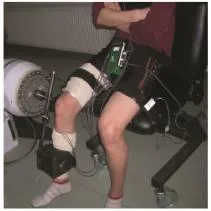
图1 伸膝肌群极限功率保持能力测试图示Figure 1.The Retentive Capacity of Muscular Peak Power Test for Knee Extensor

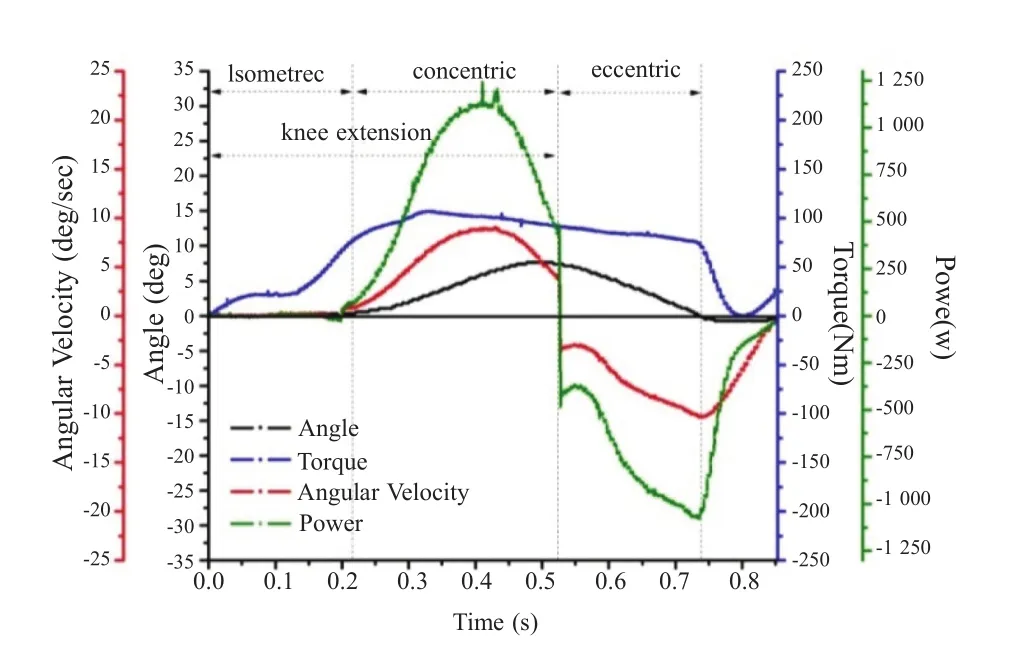
图2 伸膝肌群极限功率保持能力测试中角度、角速度、扭矩与功率随时间变化关系Figure 2.The Change of Angle，Angular Velocity，Torque and Power with Time in the Retentive Capacity of Muscular Peak Power Test

2.3.3.3 非线性人工神经网络模型法

多层感知人工神经网络模型法（Multi-Layer Perception Neural Network，MLPNN）能很好地反映肌肉疲劳程度与sEMG信号的关系［21］，用MLPNN预测极限功率损失率的步骤如下：

1.预处理阶段。用C语言编制可执行程序以完成数据的预处理，将数据转换成MatlabR2014a软件可读取的数据格式。具体步骤为：首先，提取股内侧肌、股直肌与股外侧肌3块肌肉的sEMG数据及对应的扭矩、角速度与功率数据，采用相邻平均法（Adjacent Averaging）平滑处理后，以“角速度”大于“0”对应的起止时间点截取相对应的功率与sEMG数据；其次，计算sEMG数据的4个时频特征值，如平均绝对值（Mean Absolute Value，MAV）、过零率（Zero Crossings，ZC）、斜率符号变化值（Slope Sign Changes，SSC）与波长（Wavelength，WL）［11，18，19，21］；最后，求取每位受试者sEMG数据的所有特征值，并将全部受试者的所有特征值合并。

2.人工神经网络处理阶段。使用MatlabR2014a软件的人工神经网络工具箱（Neural Network Toolbox）建立多层感知人工神经网络（Multi-Layer Perception Neural Network）模型，其中，训练函数采用Levenberg-Marquardt反向传播算法（Levenberg-Marquardt Back Propagation，LMBP），学习函数采用动量梯度下降权值和阈值学习函数（Gradient Descent Weight and Bias Learning Function）［18，19，21］。其余参数设置：隐藏层节点数为10个，训练最大次数设置为100次，训练的目标结果最大均方差设置为0.00004，学习速率设置为0.1，最大失败次数设置为18次。

将33位受试者的功率与特征值数据分为5组，其中1组为测试集，其余4组为训练集，依次循环，进行5次人工神经网络的训练-预测过程。保证每1组都能作为测试集，参与过1次人工神经网络的训练-预测过程。针对每一次神经网络的训练-预测过程，首先，将训练集的功率作为训练网络的目标值，训练集的特征值作为训练的输入值，训练人工神经网络以获取模型；其次，将测试集的功率作为真实值，测试集的特征值作为输入值，通过训练获取的模型预测测试集的功率，依次循环50次取均值作为估计值；最后，将5组人工神经网络训练-预测过程中功率的全部真实值（Actual Value）与估计值（Estimated Value）比较，以整体评价人工神经网络模型的优劣。

2.3.3.4 伸膝肌群极限功率损失率的预测性能

单个或多个线性时域参数、频域参数与瞬时频率参数，以及非线性人工神经网络提取的功率估计值，均用于预测人体神经肌肉系统输出功率损失率，两法的预测性能以信噪比（Signal-to-Noise Ratio，SNR）量化［18，21，22］（公式1）。

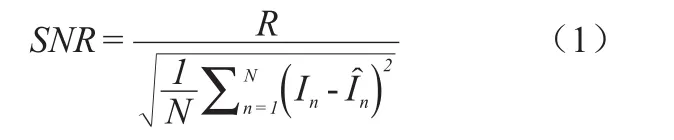
其中，分子R为BTE primusRS系统真实输出功率的变化区间（R=Imax-Imin），即输出功率变化率最大值与最小值的差值；分母为极限功率保持能力测试中伸膝肌群完成N次收缩过程中真实功率（In）与估计功率的标准误差（Root Mean Square Error，RMSE）。

2.2.4 数据的统计学分析

实验所得数据的正态性检验采用单样本K-S检验（One-Sample K-S），连续性变量以均数±标准差（±SD）或中位数［四分位差（25%～75%）］表示。3次等长峰值力矩的差异性检验采用单因素方差分析（One-Way ANOVA）与多重比较（Multiple Comparisons）。应用线性回归描述IMNF、IMDF随着伸膝次数增加而下降的趋势，并求取均值（Mean）、标准差（Standard）、斜率（Slope）、截距（Interpret）与决定系数（R2），用单样本K-S检验（One-Sample K-S）对以上5个参数进行正态分布检验，采用单个总体均数t检验（或符号秩和检验）对斜率（Slope）是否与“0”有显著性差异进行检验，IMNF、IMDF的差异性检验采用配对样本t检验（Pared-Sample T Test）或非参数检验（Nonparametric Test:Two Paired Samples），股内侧肌、股直肌与股外侧肌的差异性检验采用单因素方差分析（One-Way ANOVA）与多重比较（Multiple Comparisons），表面肌电时频参数变化率与极限功率损失率之间的相关性分析采用Person简单相关分析（Person Correlation Coefficients）与多重线性回归分析（Multiple Linear Regression）。采用多重线性回归分析（Multiple Linear Regression，MR）与人工神经网络分析（Neural Network，NN）两法拟合股内侧肌、股直肌与股外侧肌极限功率损失率估计值（Estimated Changes in Power）与真实值（Actual Changes in Power）的相关关系，拟合所得两条直线斜率（Slope）与截距（Interpret）的差异性检验采用F检验或等价t检验。

3 研究结果

3.1 伸膝肌群极限功率保持能力的测量结果

40位受试者伸膝肌群极限功率保持能力的测量结果如图3所示，膝关节110°时等长峰值力矩（The Isometric Peak Torque，IPT）3次测量结果分别为168.93±29.52 Nm、163.50± 28.88 Nm和166.92±29.11 Nm，均值为166.45±27.53 Nm，变异系数（Coefficient of Variation，CV）为5.11±2.63，3次测量值之间无显著性差异（P＝0.703）。受试者在各自50%IPT阻力矩设置下，伸膝肌群极限功率保持能力测量结果的总功、距离与时间分别为1 407.28±456.93 J、1 582.90±635.88 deg与35.20±8.77 s。

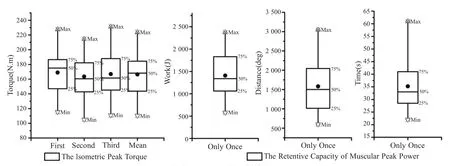
图3 伸膝肌群极限功率保持能力测量结果Figure 3.The Retentive Capacity of Muscular Peak Power for Knee Extensor

由表面肌电仪同步记录的时间（Time）、角度（Angle）、角速度（Angular Velocity）、扭矩（Torque）与功率（Power），以及3块肌肉的sEMG数据，有7位受试者因数据异常而未进行后续的分析。剩余33位受试者伸膝肌群极限功率保持能力测试中重复性伸膝次数、极限功率与极限功率损失率的变化特征如图4所示，受试者完成重复性伸膝动作的次数为31.42±9.55次，变化区间为17～56次；仅有4位受试者重复性伸膝动作的次数超过了40次，因个体间差异较大，导致40次以上极限功率损失率的变化无明显规律；但是，33位受试者前40次伸膝动作极限功率损失率呈现明显的下降趋势；受试者伸膝动作极限功率后5次均值（377.47±77.39 W）显著低于前5次均值（606.21±104.64 W），下降了37.73%（P＜0.01）。

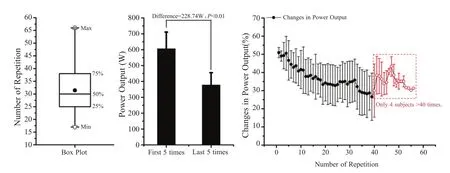
图4 伸膝肌群极限功率保持能力测试中重复性伸膝次数、极限功率与极限功率损失率的变化图Figure 4.The Iepetition of Knee Extension，Muscular Peak Power and Rate of Peak Power Loss during the Retentive Capacity of Muscular Peak Power for Knee Extensor

3.2 伸膝肌群表面肌电瞬时频率参数的测量结果

伸膝肌群瞬时频率参数IMNF与IMDF随重复性伸膝次数增加而下降趋势的线性拟合结果如表1所示，简单线性回归方程的198项（33位受试者×2个肌电参数×3块肌肉）截距值皆为正值，198项斜率值皆为负值，且斜率值与“0”相比均具有非常显著性差异（P＜0.01），即股内侧肌、股直肌与股外侧肌的瞬时频率参数IMNF与IMDF均呈显著性下降趋势。

瞬时频率参数IMNF与IMDF均值（Mean）、标准差（Standard）、斜率（Slope）、截距（Interpret）与决定系数（R2）的差异性比较表明，股内侧肌、股直肌与股外侧肌瞬时频率参数的均值IMNF均小于IMDF，且均具有显著性差异（P＜0.05）。股内侧肌、股直肌与股外侧肌瞬时频率参数的标准差值IMNF均大于IMDF，且均具有非常显著性差异（P＜0.01）。股内侧肌斜率值IMNF小于IMDF，股直肌与股外侧肌斜率值IMNF大于IMDF，但均无显著性差异（P＜0.05）。股内侧肌、股直肌与股外侧肌瞬时频率参数的截距IMNF均小于IMDF，且均具有显著性差异（P＜0.05）。股内侧肌、股直肌与股外侧肌瞬时频率参数的决定系数值IMNF均小于IMDF，且均具有非常显著性差异（P＜0.01）。

股内侧肌、股直肌与股外侧肌瞬时频率参数IMNF与IMDF的差异性比较表明，瞬时频率参数IMNF与IMDF的斜率值由大至小的顺序一致，均为股直肌→股外侧肌→股内侧肌；且股内侧肌与股直肌相比，具有显著性差异（P＜0.05）；股直肌与股外侧肌相比，无显著性差异（P＞0.05）。

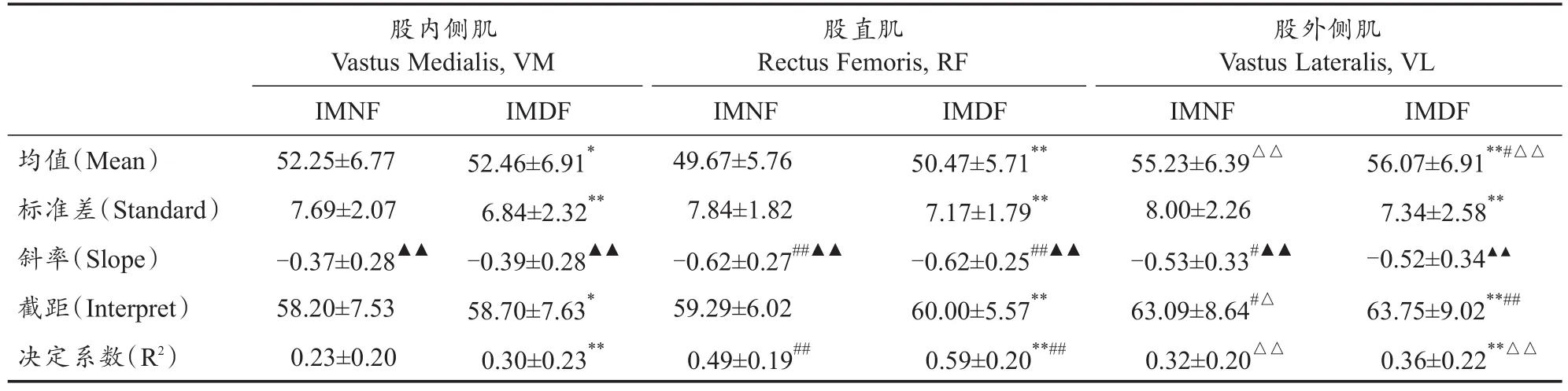
表1 伸膝肌群极限功率保持能力测试中表面肌电瞬时频率参数Table 1 The Instantaneous Frequency Parameters of Surface Electromyography during the Retentive Capacity of Muscular Peak Power for Knee Extensor

3.3 线性时频参数变化率与极限功率损失率的相关关系及信噪比值

33位受试者线性时频参数变化率与极限功率损失率的相关系数及信噪比值如表2与图5所示，时域参数与Power%相关系数的绝对值，RMS%大于MAV%，相关性均较差（－0.047 0～－0.186 5）；频域参数与Power%的相关系数，MDF%大于MNF%，相关性均较差（0.023 8～0.228 1）；瞬时频率参数与Power%的相关系数，IMDF%大于IMNF%，呈低度至中度相关（0.211 3～0.476 6），且具有较高的信噪比值（SNR=8.25～9.22）。3组时频参数与Power%相关系数的绝对值，3块肌肉从大至小的顺序皆不同，RMS%与MAV%为VM→VL→RF，MNF%与MDF%为RF→VM→VL，IMNF%与IMDF%为RF→VL→VM。

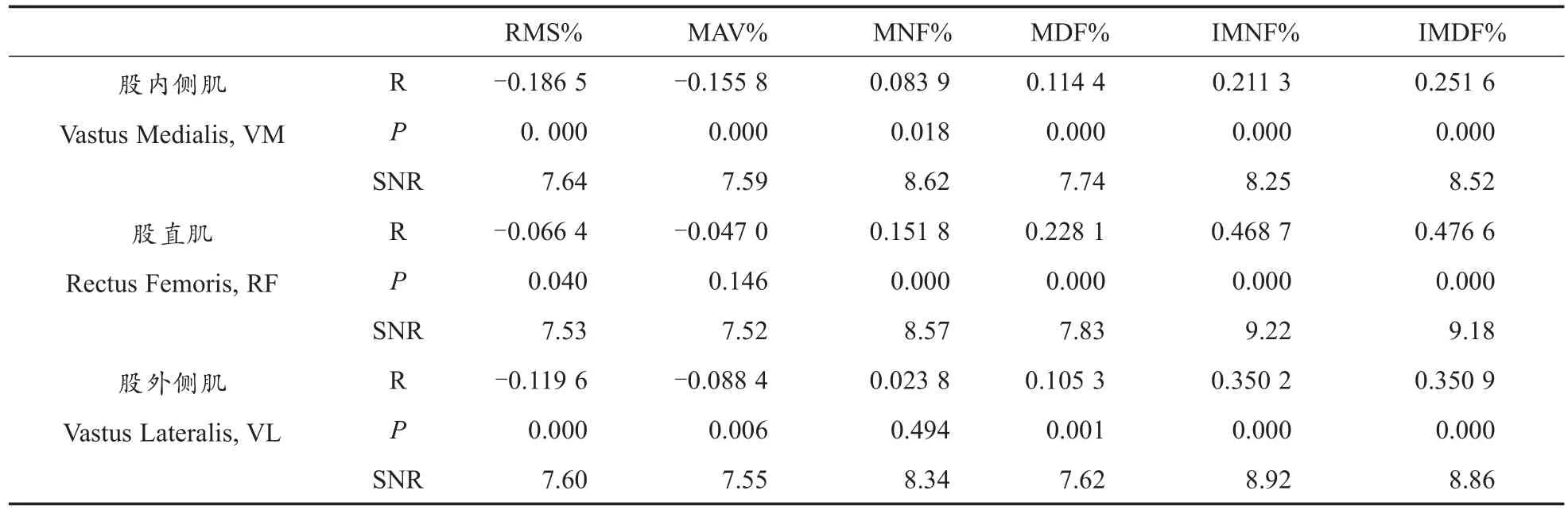
表2 线性时频参数变化率与极限功率损失率的相关系数及信噪比值Table 2 Percent Changes of Linear Time-Frequency Parameters against Percent Changes of Peak Power Output and Signal-to-Noise Ratio

直线相关相关系数的平方（r2）等于简单线性回归方程的决定系数（R2），后者数值的大小反映了回归关系能解释因变量总变异的百分比，即IMNF%、IMDF%能单独解释股内侧肌极限功率损失率（Power%）4.46%、6.33%的方差变异（performance variance of changes）（P＜0.01），能单独解释股直肌极限功率损失率（Power%）21.97%、22.71%的方差变异（P＜0.01），能单独解释股外侧肌极限功率损失率（Power%）12.26%、12.31%的方差变异（P＜0.01；表2、图5）。

3.4 线性回归法与非线性神经网络法预测极限功率损失率的差异

由sEMG时频参数多重线性回归方程的复相关系数（R）与方程式可知（表3），IMDF%联合MDF%一起能解释股内侧肌极限功率损失率6.95%的方差变异（Performance Variance，PV），较IMDF%单独能解释的方差变异（6.33%）提高了0.62%，且具有较高的信噪比值（SNR=8.38）。IMDF%联合MDF%、MNF%、RMS%一起能解释股直肌极限功率损失率25.93%的方差变异，较IMDF%单独能解释的方差变异（22.71%）提高了3.22%，且具有较高的信噪比值（SNR=10.06）。IMDF%联合MDF%、MNF%一起能解释股外侧肌极限功率损失率16.05%的方差变异，较IMDF%单独能解释的方差变异（12.31%）提高了3.74%，且具有较高的信噪比值（SNR=9.41）。

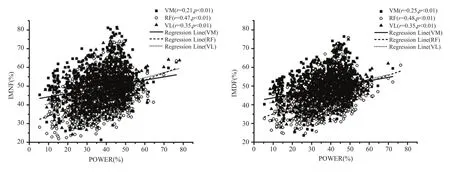
图5 基于小波变换法求取的瞬时频率参数变化率与极限功率损失率的相关关系Figure 5.Percent Changes of Instantaneous Frequency Parameters（%of the first two repetitions）against Percent Changes of Peak Power Output for all the subjects

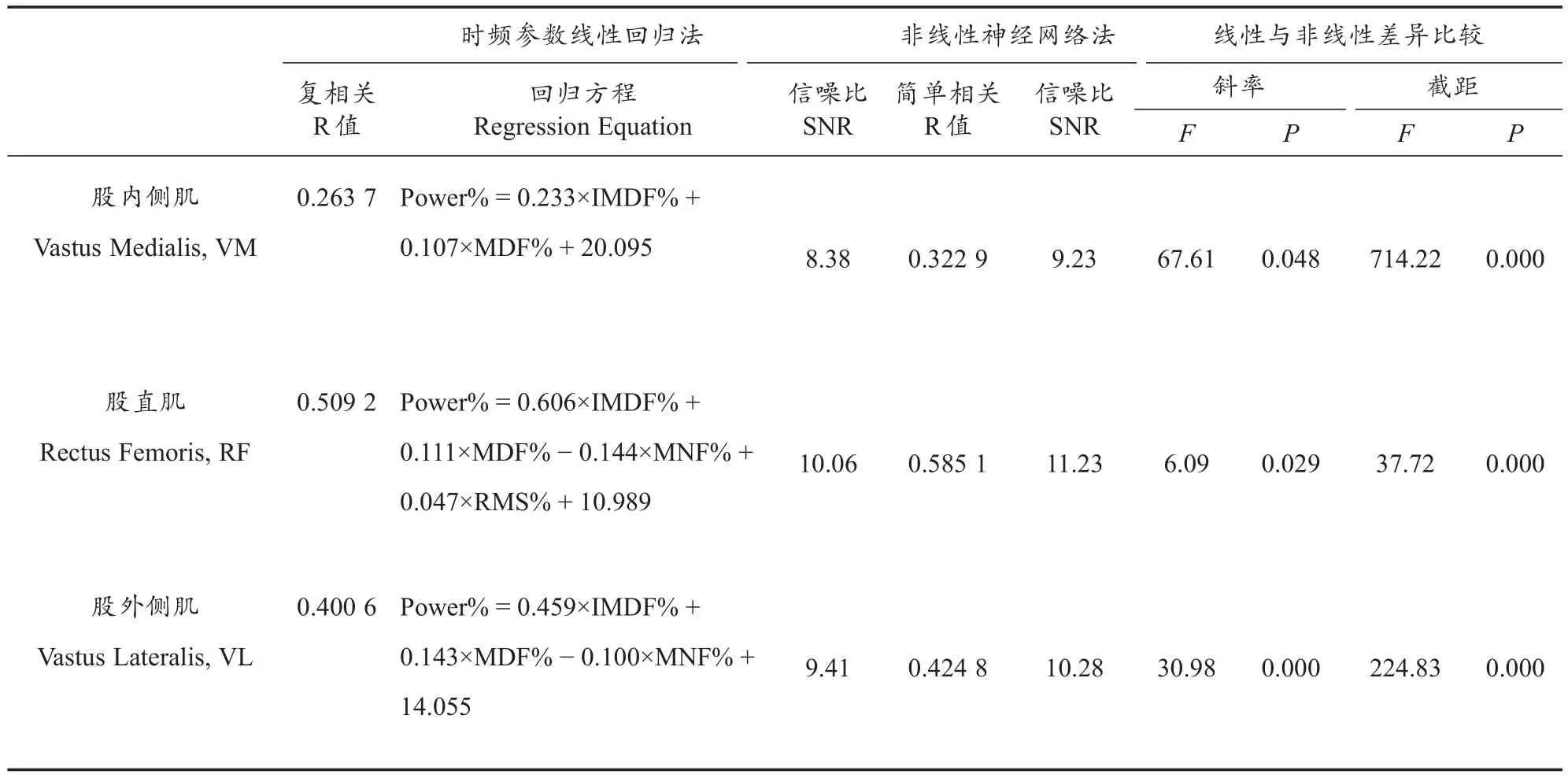
表3 线性回归法与非线性神经网络法预测极限功率损失率的差异比较Table 3 The Statistical Significance between Linear Regression and Non-Linear Neural Network for Predicting the Changes of Peak Power

伸膝肌群极限功率损失率由非线性神经网络法求取的估计值（Estimated changes in power）与真实值（Actual changes in power）的相关关系如表3与图6所示，神经网络法能解释股内侧肌极限功率损失率10.43%的方差变异（Performance Variance，PV），较线性时频参数法能解释的方差变异（6.95%）提高了3.47%，且具有较高的信噪比值（SNR=9.23）；能解释股直肌极限功率损失率34.23%的方差变异，较线性时频参数能解释的方差变异（25.93%）提高了8.31%，且具有较高的信噪比值（SNR=11.23）；能解释股外侧肌极限功率损失率18.05%的方差变异，较线性时频参数能解释的方差变异（16.05%）提高了2.00%，且具有较高的信噪比值（SNR=10.28）。而且，线性与非线性两法拟合所得两条直线的斜率（Slope）与截距（Interpret）均具有显著性差异（P＜0.05）。

Figure 6.Actual vs.Estimated Changes in Peak Power Output Obtained for Both Approaches（Linear and Non-Linear Models）

4 分析与讨论

4.1 伸膝肌群极限功率保持能力与功率损失率的变化特征

人类日常活动动作可用克服恒定负荷下肢体环节运动速度冲击正弦曲线式变化所描述，在一系列预负荷（IPT%）阻力设置的测试中，预负荷（阻力矩值）与测试系统的角速度成线性关系［28］，极限功率出现在阻力矩与角速度值均接近其最大值的50%时［39］。静态肌力与关节角度的力量曲线关系表明［1，4］，伸膝肌群在膝关节屈曲110°时杠杆效率最高，此关节角度下的等长肌力值即为IPT。本研究表明，50%IPT阻力设置是受试者重复性伸膝动作中能克服的最大阻力，每次完成屈伸动作幅度的时间接近1 s；重复性伸膝约31.42次（17.0～56.0次）、持续时间约35.20 s（22.0～61.0 s），在短时间内即可完成伸膝肌群极限功率保持能力的测量。说明确保除时间外其他变量的一致性，人体单关节肌群极限功率的保持能力可通过受试者输出的工作量或是活动的持续时间来量化，这为建立科学合理的人体神经肌肉系统极限功率保持能力的定量评价方法提供了理论依据［1］。但目前有关健康人简单运动中单关节肌群极限功率保持能力的测评却极为罕见，未找到相类似的研究提供可比对的数据。

肌肉疲劳程度的直接检测法以检测神经肌肉系统的最大抗阻能力为主，常用受试者特定肌群输出肌力或功率能力的下降来定义疲劳［8，16］。前者以受试者静力性等长肌力不能维持在所要求的水平，并以肌力的稳定下降来测量疲劳［15］；后者则以受试者动态重复性工作过程中肢体环节运动速度的减慢，和/或输出功率的变化来测量疲劳［24］。Mallor等［31］曾发现，在动态重复性伸膝运动伸膝肌群的向心收缩阶段，运动环节呈现先加速后减速的变化特征，并形成一低一高差异悬殊的两次功率波峰，随着伸膝次数的增加输出功率曲线整体上呈渐进式地变平趋势，可用第2次功率波峰值（Peak Power）的下降趋势来定义神经肌肉系统的疲劳程度［31］。本研究也表明，受试者伸膝肌群极限功率保持能力虽存在着较大的个体差异，但随着重复性伸膝次数的增加，第2次功率波峰整体上呈明显的下降趋势，伸膝肌群输出的功率峰值下降了近40%。

4.2 线性时频参数预测伸膝肌群极限功率损失率的准确性

sEMG幅值与频谱参数常用于监测肌肉静态等长收缩中的疲劳程度。然而，肌肉动态收缩时sEMG信号的不平稳性会引起上述参数的变异性增强，如探测电极周围活化运动单位的募集程度，时变空间滤波器（Time-Varying Spatial Filter）随肌肉形状改变、神经支配区与表面电极间的相对运动而产生的变化情况等［35］。sEMG幅值参数受活化运动单位的数目、放电率，以及细胞内动作电位（Intracellular Action Potential，IAP）形状与传播速度的影响［14］。不同实验方案中肌电幅值与肌力之间的关系存在着差异［13］，肌肉动态工作中曾观察到次最大动态活动中sEMG幅值增大与最大随意收缩活动中幅值变小的现象［19］，细胞内动作电位的延长效应可能是导致实验结果自相矛盾的原因［6］。本研究也表明，肌电幅值变化率（RMS%、MAV%）与功率损失率（Power%）之间的相关系数较低（－0.0470～－0.1865），相关性较差（r＜0.20）。sEMG频谱参数与肌纤维传导速度的变化，以及随后的运动单位动作电位波形持续时间的改变有关［29，36］。一些研究曾观察到动态疲劳工作中平均功率频率（Mean Power Frequency）的减退［40］，然而，在动态步行训练研究中并未发现此指标有任何改变［5］。肌间温度与肌肉疲劳均能引起频谱成分的改变，前者使频谱转向高谱，后者恰好相反，动态工作中两者的补偿效应可能是实验结果不一致的原因［19］。本研究也表明，肌电频率参数变化率与功率损失率之间的相关系数MDF要大于MNF，仅肌直肌MDF与功率损失率呈低度相关（r= 0.2281）。

CWT时频分析法通过一函数族构成函数空间框架，将原始信号按照时间对应关系分解到不同频带上或对信号进行不同的精度表达，同时提供信号时域和频域两方面信息，从而达到分析非平稳sEMG信号的目的［12，27］。瞬时频谱参数IMNF、IMDF是平稳sEMG信号中MNF、MDF含义在非平稳信号中的扩展，IMDF是功率谱上使左右两边能量相等的点，即重心所对应的频率值，IMNF是功率谱定义范围内平均功率对应的频率值，同一sEMG信号的IMDF与IMNF之间存在着偏差［10，11，33］。本研究也发现，同一块肌肉sEMG瞬时频率参数均值IMDF大于IMNF，而标准差IMDF小于IMNF，即参数的统计学特征为IMDF平均水平高但离散水平低。应用时频与时间尺度技术（Time–Frequency and Time–Scale Techniques）时会出现低频转移现象［7，10］，肌肉动态工作中的瞬时频率参数（Instantaneous Frequency，IF）会随着疲劳的发展而降低［10，11，33］。本研究与之相符，伸膝肌群IMDF、IMNF 2个线性回归直线的斜率皆为负值，但2个斜率值之间并无显著性差异，说明两者均能很好地描绘肌肉的疲劳现象。因IMDF均值大于IMNF，导致2个线性回归直线的截距前者大于后者。然而，2个线性回归直线的拟合优度（R2）IMDF要好于IMNF。另外，本研究也证实，瞬时频率参数与Power%的相关系数，以及能单独解释伸膝肌群极限功率损失率的方差变异比率，IMDF%均大于IMNF%。综合瞬时频率参数的统计学特征与线性拟合优度及预测疲劳的准确度可知，在用于监测动态工作过程中神经肌肉系统的疲劳发展程度时，IMDF的性能要优于IMNF［10，26］。IMNF、IMDF两参数线性回归直线的斜率值，3块肌肉以股直肌最大，股外侧肌居中，股内侧肌最小；瞬时频率参数与Power%的相关系数，以及能单独解释伸膝肌群极限功率损失率的方差变异比率，3块肌肉从大至小的顺序也皆为股直肌、股外侧肌、股内侧肌。以往在伸膝肌群动态重复性疲劳测试［7，18，34，25］与静态等长持续性收缩测试中［9，32］也曾观察到类似现象，这可能与伸膝肌群3块肌肉肌纤维类型不同［7］及动态重复性工作过程中先等长-再向心-后离心的收缩形式［34］有关。

疲劳监测的线性技术是基于sEMG时频特征参数变化率与肌肉功率损失率（肌肉疲劳的直接测定法）之间的线性回归分析，有研究表明，应用不同的sEMG时频参数及多个参数的组合，能较为准确地追踪动态工作中神经肌肉系统的疲劳程度［20，22］。为适应人体神经肌肉系统动态工作能力基础数据采集与电生理评价时，对选测指标易于标准化，代表性、稳定性强等要求，本研究基于较为常见的sEMG时频参数线性回归法，也发现与单独应用瞬时频率参数变化率（IMDF%、IMNF%）相比，瞬时频率参数变化率结合时频参数变化率（MNF%、MDF%、RMS%）能提高预测伸膝肌群极限功率损失率（Power%）的准确度。

4.3 非线性神经网络分析预测伸膝肌群极限功率损失率的准确性

肌肉疲劳监测的非线性技术是以与疲劳相关的sEMG时频特征参数（MAV、ZC、SSC、WL）为特征值（神经元）的人工神经网络预测模型，神经网络法与线性技术相比，优点在于其能学习sEMG时频特征参数与肌肉疲劳之间的关系［19，23］。MacIsaac等［30］曾基于多层感知人工神经网络模型综合肌电信号幅值与频率特征等多个sEMG参数的信息，首次应用此项技术获取一个随时间呈线性变化的疲劳指数（Mapping Index，MI）。与单一sEMG参数（MNF或 IMNF）相比，MI能较为准确地追踪不同屈肘运动中肌肉疲劳的变化特征，其SNR值在随意运动与静态收缩条件下高达7.89和9.69，表明估计值与真实值之间的误差较小［30］。肌肉疲劳时MI随时间呈线性下降趋势，然而，疲劳的直接测定法，如等速模式下的最大随意收缩力量并非呈线性下降［17］。因此，MI可能无法反映等速模式下重复性伸膝动作中的肌力损失。针对MI参数的局限性，Gonzalez-Izal等［18］提倡以机械力作为神经网络预测模型的目标函数（Objective Function）来修正初始模型，来代替先验（Priori）随时间推移线性变化的疲劳指数，并证明此项技术能更为准确地追踪伸膝动作中肌肉疲劳的变化特征。因此，本研究将受试者伸膝肌群极限功率（Power）作为目标函数，以MAV、ZC、SSC、WL 4个sEMG时频特征参数作为特征值，建立非线性多层感知人工神经网络预测模型。本研究表明，综合多个sEMG时频参数信息的线性与非线性技术，均能很好地追踪神经肌肉系统动态工作过程中输出功率损失的变化特征，基于连续性小波变换法提取的瞬时频率参数IMDF%能单独解释股直肌极限功率损失率（Power%）的方差变异达到22.71%（SNR=9.18），联合MDF%、MNF%、RMS%一起能解释的方差变异提高到25.93%（SNR=10.06），而神经网络法能解释的方差变异高达34.23%（SNR=11.23），且信噪比值表明以上神经肌肉系统功率损失率预测方法的性能与稳健性逐步提升。

线性与非线性技术的区别在于，非线性神经网络法是基于一个学习程序调整权重以估算sEMG时频特征参数与肌肉疲劳之间的关系，而线性技术则将两者的关系假定为线性的先验。而且，与线性预测模型相比，人工神经网络模型的学习程序计算量大，计算过程耗时较长［19］。Gonzalez-Izal等［21］曾比较线性与非线性追踪肌肉功率损失率的准确性差异，证实神经网络法获取的功率估计值与真实值之间的相关系数较大，且具有较高的SNR值，用于预测功率损失率时误差更小。本研究也证实，用于预测伸膝肌群极限功率损失率时，非线性法估计值与真实值的相关系数要大于线性法（0.322 9 vs.0.263 7，VM；0.585 1 vs.0.509 2，RF；0.424 8 vs.0.400 6，VL），具有更高的SNR值（9.23 vs.8.38，VM；11.23 vs.10.06，RF；10.28 vs.9.41，VL），且功率损失率估计值与真实值拟合所得直线的斜率与截距之间有显著性差异，表明非线性神经网络模型法预测肌肉功率损失率的估计误差（Estimation Errors，EE）较小，准确性要好于sEMG时频参数线性回归法。

5 结论与建议

sEMG时频特征参数线性回归技术与非线性人工神经网络技术，均能很好地追踪人体神经肌肉系统动态工作疲劳过程中机械输出功率的损失，但后者用于追踪肌肉功率损失率的准确性要优于前者。

本研究仅比较了常见sEMG时频特征参数线性回归法与非线性人工神经网络法预测人体神经肌肉系统功率损失率的准确性，以适应人体神经肌肉系统动态工作能力基础数据采集时，对选测指标易于标准化，代表性、稳定性强的要求，未能考察其他有意义的sEMG时频特征参数。实践应用时可权衡预测精度与计算工作量的要求，选取相应的sEMG分析技术，用于动态工作疲劳过程中神经肌肉系统功能能力的电生理评价。

［1］史冀鹏，徐红旗，张欣，等.运用BTE Primus～（RS）系统测定人体下肢单关节肌群极限功率与肌耐力的方法学研究［J］.天津体育学院学报，2012（2）:162-167.

［2］徐红旗，史冀鹏，倪维广，等.人体单关节肌群极限功率发展与保持能力研究进展［J］.中国运动医学杂志，2013（5）: 443-52.

［3］徐红旗，史冀鹏，张欣，等.表面肌电小波变换分析技术监测重复性手工提放重物作业中机体肌肉疲劳的研究［J］.体育科学，2011（12）:44-54.

［4］徐红旗，张欣，冉令华，等.应用等张模式测定人体单关节肌群功率发展与保持能力的方法学研究［J］.人类工效学，2011，17（4）:13-18.

［5］AMENT W，BONGA G J，HOF A L，et al.Electromyogram median power frequency in dynamic exercise at medium exercise intensities［J］.Eur J Appl Physiol Occup Physiol，1996，74（1-2）:180-186.

［6］ARABADZHIEY T I，DIMITROV V G，DIMITROVA N A，et al.Interpretation of EMG integral or RMS and estimates of "neuromuscular efficiency"can be misleading in fatiguing contraction［J］.J Electromyography Kinesiol，2010，20（2）:223-232.

［7］BECK T W，STOCK M S，DEFREITAS J M.Shifts in EMG spectral power during fatiguing dynamic contractions［J］.Muscle Nerve，2014，50（1）:95-102.

［8］BIGLAND-RITCHIE B，DONOVAN E F，ROUSSOS C S. Conduction velocity and EMG power spectrum changes in fatigue of sustained maximal efforts［J］.J Appl Physiol，1981，51（5）:1300-1305.

［9］BILODEAU M，SCHINDLER-IVENS S，WILLIAMS DM，et al.EMG frequency content changes with increasing force and during fatigue in the quadriceps femoris muscle of men and women［J］.J Electromyogr Kinesiol，2003，13（1）:83-92

［10］BONATO P，ROY S H，KNAFLITZ M，et al.Time-frequency parameters of the surface myoelectric signal for assessing muscle fatigue during cyclic dynamic contractions［J］.IEEE T Bio-Med Eng，2001，48（7）:745-753.

［11］BUENO D R，LIZANO J M，MONTANO L.Muscular fatigue detection using sEMG in dynamic contractions［C］//Conference proceedings:Annual International Conference of the IEEE Engi neering in Medicine and Biology Society IEEE Engineering in Medicine and Biology Society Annual Conference，2015，25-29（8）:494-497.

［12］CIFREK M，MEDVED V，TONKOVIC S，et al.Surface EMG based muscle fatigue evaluation in biomechanics［J］.Clin Biomech，2009，24（4）:327-340.

［13］DIDERIKSEN J L，FARINA D，ENOKA R M.Influence of fatigue on the simulated relation between the amplitude of the surface electromyogram and muscle force［J］.Philos Transact A Math Phys Eng Sci，2010，368（1920）:2765-2781.

［14］DIMITROVA N A，DIMITROV G V.Amplitude-related characteristics of motor unit and M-wave potentials during fatigue.A simulation study using literature data on intracellular potential changes found in vitro［J］.J Electromyogr Kinesiol，2002，12（5）:339-349.

［15］ENOKA R M，DUCHATEAU J.Muscle fatigue:what，why and how it influences muscle function［J］.J Physiol，2008，586（1）:11-23

［16］FITTS R H.Cellular mechanisms of muscle fatigue［J］.Physiol Rev，1994，74（1）:49-94.

［17］GERDLE B，LARSSON B，KARLSSON S.Criterion validation of surface EMG variables as fatigue indicators using peak torque:a study of repetitive maximum isokinetic knee extensions［J］.J Electromyogr Kinesiol，2000，10（4）:225-232.

［18］GONZALEZ-IZAL M，FALLA D，IZQUIERDO M，et al.Predicting force loss during dynamic fatiguing exercises from nonlinear mapping of features of the surface electromyogram［J］.J Neurosci Methods，2010，190（2）:271-278.

［19］GONZALEZ-IZAL M，MALANDA A，GOROSTIAGA E，et al.Electromyographic models to assess muscle fatigue［J］.J Electromyogr Kinesiol，2012，22（4）:501-512.

［20］GONZALEZ-IZAL M，MALANDA A，NAVARRO-AMEZQUETA I，et al.EMG spectral indices and muscle power fatigue during dynamic contractions［J］.J Electromyogr Kinesiol，2010，20（2）:233-240.

［21］GONZALEZ-IZAL M，MALANDAA，RODRIGUEZ-CARRENO I，et al.Linear vs.non-linear mapping of peak power using surface EMG features during dynamic fatiguing contractions［J］.J Biomech，2010，43（13）:2589-2594.

［22］GONZALEZ-IZAL M，RODRIGUEZ-CARRENO I，MALANDA A，et al.sEMG wavelet-based indices predicts muscle power loss during dynamic contractions［J］.J Electromyogr Kinesiol，2010，20（6）:1097-1106.

［23］HUNG C C，SHEN T W，LIANG C C，et al.Using surface electromyography（SEMG）to classify low back pain based on lifting capacity evaluation with principal component analysis neural network method［C］//Conference proceedings:Annual International Conference of the IEEE Engineering in Medicineand Biology Society IEEE Engineering in Medicine and Biology Society Annual Conference，2014，26-30（8）:18-21.

［24］IZQUIERDO M，GONZALEZ-BADILLO J J，HAKKINEN K，et al.Effect of loading on unintentional lifting velocity declines during single sets of repetitions to failure during upper and lower extremity muscle actions［J］.Int J Sports Med，2006，27（9）:718-724.

［25］KARLSSON J S，OSTLUND N，LARSSON B，et al.An estimation of the influence of force decrease on the mean power spectral frequency shift of the EMG during repetitive maximum dynamic knee extensions［J］.J Electromyogr Kinesiol，2003，13（5）:461-468.

［26］KARLSSON S，YU J，AKAY M.Time-frequency analysis of myoelectric signals during dynamic contractions:a comparative study［J］.IEEE T Bio-Med Eng，2000，47（2）:228-238.

［27］KILBY J，HOSSEINI HG.Extracting effective features of SEMG using continuous wavelet transform［C］//Conference proceedings:Annual International Conference of the IEEE Engineering in Medicine and Biology Society IEEE Engineering in Medicine and Biology Society Annual Conference，2006，15（8-9）:1704-7.

［28］KOJIMA T.Force-velocity relationship of human elbow flexors in voluntary isotonic contraction under heavy loads［J］.Int J Sports Med，1991，12（2）:208-213.

［29］KOUZAKI M，SHINOHARA M，MASANI K，et al.Force fluctuations are modulated by alternate muscle activity of knee extensor synergists during low-level sustained contraction［J］.J Appl Physiol，2004，97（6）:2121-2131.

［30］MACISAAC D T，PARKER P A，ENGLEHART K B，et al. Fatigue estimation with a multivariable myoelectric mapping function［J］.IEEE T Bio-Med End，2006，53（4）:694-700.

［31］MALLOR F，LEON T，GASTON M，et al.Changes in power curve shapes as an indicator of fatigue during dynamic contractions［J］.J Biomech，2010，43（8）:1627-1631.

［32］MANNION A F，DOLAN P.Relationship between myoelectric and mechanical manifestations of fatigue in the quadriceps femoris muscle group［J］.Eur J Appl Physiol Occup Physiol，1996，74（5）:411-419.

［33］MOLINARI F，KNAFLITZ M，BONATO P，et al.Electrical manifestations of muscle fatigue during concentric and eccentric isokinetic knee flexion-extension movements［J］.IEEE T Bio-Med Eng，2006，53（7）:1309-1316.

［34］PINCIVERO DM，GANDHI V，TIMMONS M K，et al.Quadriceps femoris electromyogram during concentric，isometric and eccentric phases of fatiguing dynamic knee extensions［J］.J Biomech，2006，39（2）:246-254.

［35］ROGERS D R，MACISAAC D T.A comparison of EMG-based muscle fatigue assessments during dynamic contractions［J］.J Electromyogr Kinesiol，2013，23（5）:1004-1011.

［36］ROMAN-LIU D.The influence of confounding factors on the relationship between muscle contraction level and MF and MPF values of EMG signal:a review［J］.Int J Occup Saf Ergo，2016，22（1）:77-91.

［37］SAPEGAAA，DRILLINGS G.The definition and assessment of muscular power［J］.J Orthop Sports Phys Ther，1983，5（1）:7-9.

［38］SRHOJ-EGEKHER V，CIFREK M，MEDVED V.The application of Hilbert-Huang transform in the analysis of muscle fatigue during cyclic dynamic contractions［J］.Med Biol Eng Comput，2011，49（6）:659-669.

［39］STAUBER WT，BARILL ER，STUABER RE，et al.Isotonic dynamometry for the assessment of power and fatigue in the knee extensor muscles of females［J］.Clin Physiol，2000，20（3）:225-233.

［40］TESCH P A，DUDLEY G A，DUVOISIN M R，et al.Force and EMG signal patterns during repeated bouts of concentric or eccentric muscle actions［J］.Acta Physiol Scand，1990，138（3）:263-271.

［41］XIE H，WANG Z.Mean frequency derived via Hilbert-Huang transform with application to fatigue EMG signal analysis［J］. Comput Methods Programs Biomed，2006，82（2）:114-120.

Linear Regression vs.Non-Linear Neural Network Predicts Power Loss Rate using sEMG Time-Frequency Features during the Retentive Capacity of Muscular Peak Power Test for Knee Extensor

XU Hong-qi1，SHI Ji-peng1，ZHANG Shou-wei1，XU Xin1，YANG Chuan-qi2，YANG Fan3，ZHANG Xin4，ZHAO Chao-yi4

Objective:This study compares a linear（linear regression）and a non-linear（neural network）power loss mapping using a set of features of the surface electromyogram recorded from the knee extensor during the retentive capacity of muscular peak power test.Methods:BTE PrimusRSsystem and surface electromyography instrument were synchronized，40 male college students repeated knee flexion and extension exercise to fatigue，with the load resistance for 50%of the isometric peak torque，and action frequency 60 times/min.The following variables were computed from each extension contraction:peak power loss（Power%），and the changes rate of sEMG variables such as MAV%，RMS%，MNF%，MDF%，IMNF%，IMDF%.A multi-layer perceptron neural network was established，which consists of an interconnected group of artificial neurons（MAV，ZC，SSC，WL），and used to calculate the actual and estimated changes in power. Results:IMDF%as a single parameter predictor accounted for 6.33%，22.71%，12.31%of the performance variance of changes in vastus medialis，rectus femorisa and vastus lateralis peak power，IMDF%and other time-frequency parameters as a combination predictor accounted for 6.95%，25.93%，16.05%，the estimated changes of power were calculated by a non-linear neural network accounted for 10.43%，34.23%，18.05%，and the signal to noise ratios increased gradually.Two regression lines were fitted by the actual vs.the estimated changes in power output from both linear and non-linear techniques，and the slope and intercept of two lines had a statistical significance（P＜0.05）.Conclusion:Linear regression and non-linear neural network using sEMG time-frequency features，are two useful tools to map changes in muscular power loss during dynamic fatiguing task，but the latter's accuracy is better than the former.

peak power；surface electromyography；wavelet transform；instantaneous frequency；artificial neural network

1002-9826（2017）02-0053-11

10.16470/j.csst.201702007

G804.63

：A

2016-06-04；

：2016-12-26

科技基础性工作专项（2013FY110200）；中央高校基本科研业务费资助项目（14QNJJ032）。

徐红旗，男，副教授，博士，主要研究方向为运动生物力学，E-mail:xu_hongqi0402@126.com。

张守伟，男，教授，博士研究生导师，主要研究方向为体育教育训练学，E-mail：zhangsw178@nenu.edu.cn。

1.东北师范大学，吉林长春130024；2.长春光华学院商学院，吉林长春130033；3.北京航空航天大学生物医学工程学院，北京100191；4.中国标准化研究院人类工效学标准化研究领域，北京100088

1.Northeast Normal University，Changchun 130024，China；2.Changchun Guanghua College，Changchun 130033，China；3.BeiHang University，Beijing 100191，China；4. China National Institute of Standardization，Beijing 100088，China.