一种车载平台重心偏移引起的调平误差补偿方法

马 同,任雪峰，周 泓,宋荣贵

(1.中国船舶重工集团公司第七二四研究所,南京 211153；2.海军驻南京地区雷达系统军事代表室，南京 210003)

一种车载平台重心偏移引起的调平误差补偿方法

马 同1,任雪峰2，周 泓1,宋荣贵1

(1.中国船舶重工集团公司第七二四研究所,南京 211153；2.海军驻南京地区雷达系统军事代表室，南京 210003)

对车载平台因重心偏移引起的姿态变化进行了分析,利用YXZ变换建立了姿态误差的数学模型,并根据工程实际对模型进行了简化。在姿态误差模型的基础上,设计了一套车载平台调平的误差补偿方法,并利用卡尔曼滤波器对姿态误差进行滤波。实验结果表明,本方法能够有效补偿车载平台重心偏移引起的调平误差。

车载雷达;车载平台;车载天线;重心偏移;误差补偿;YXZ变换;姿态误差

0 引 言

现代战争对雷达的工作性能要求越来越高。特别是机动陆面载体,如车载雷达、发射架等设备,到达预定位置后,要求实现快速架设和精确调平[1]。车载平台的调平精度直接影响雷达的精确性和工作可靠性。因此,提高车载平台的调平精度成为提高装备使用效能的关键措施之一。

车载平台的人工手动调平已很难满足对雷达快速架设、快速撤收,以及平台高精度调平的要求。与人工调平相比,机电液式自动调平具有调平时间短、调平精度高、可靠性高等特点,在现代调平装备中被广泛应用[2]。本文所涉及的车载天线具有结构复杂、载荷重和倾覆力矩大等特点,工作时需要先进行车载平台调平,然后才能架设天线。为了保证车载天线的安全性,要求天线架设后车载平台不可以进行二次调平。

在天线架设过程中,车载平台的重心会发生偏移,使车载平台产生形变,从而导致车载平台的水平姿态发生变化。这就需要对车载平台的模型进行分析,研究重心偏移对姿态误差的影响,采用相应的控制补偿算法,补偿车载平台重心偏移引起的调平误差。

1 车载平台模型描述

某雷达天线车主要由车载平台、调平腿、设备舱箱、天线及其架设机构等组成,其简化结构如图1所示。调平蛙腿共有4条,对称安装在车载平台上,用于车载平台的调平。天线存在收叠和架设两种状态。与收叠状态相比,架设状态下的车载平台重心将会向Y轴的负半轴方向偏移,同时会使车载平台产生弹性形变。倾角传感器安装在刚度较好的平台基准面上,位于天线架设机构下方,用于测量架设机构绕横轴(X轴)和纵轴(Y轴)的转角。

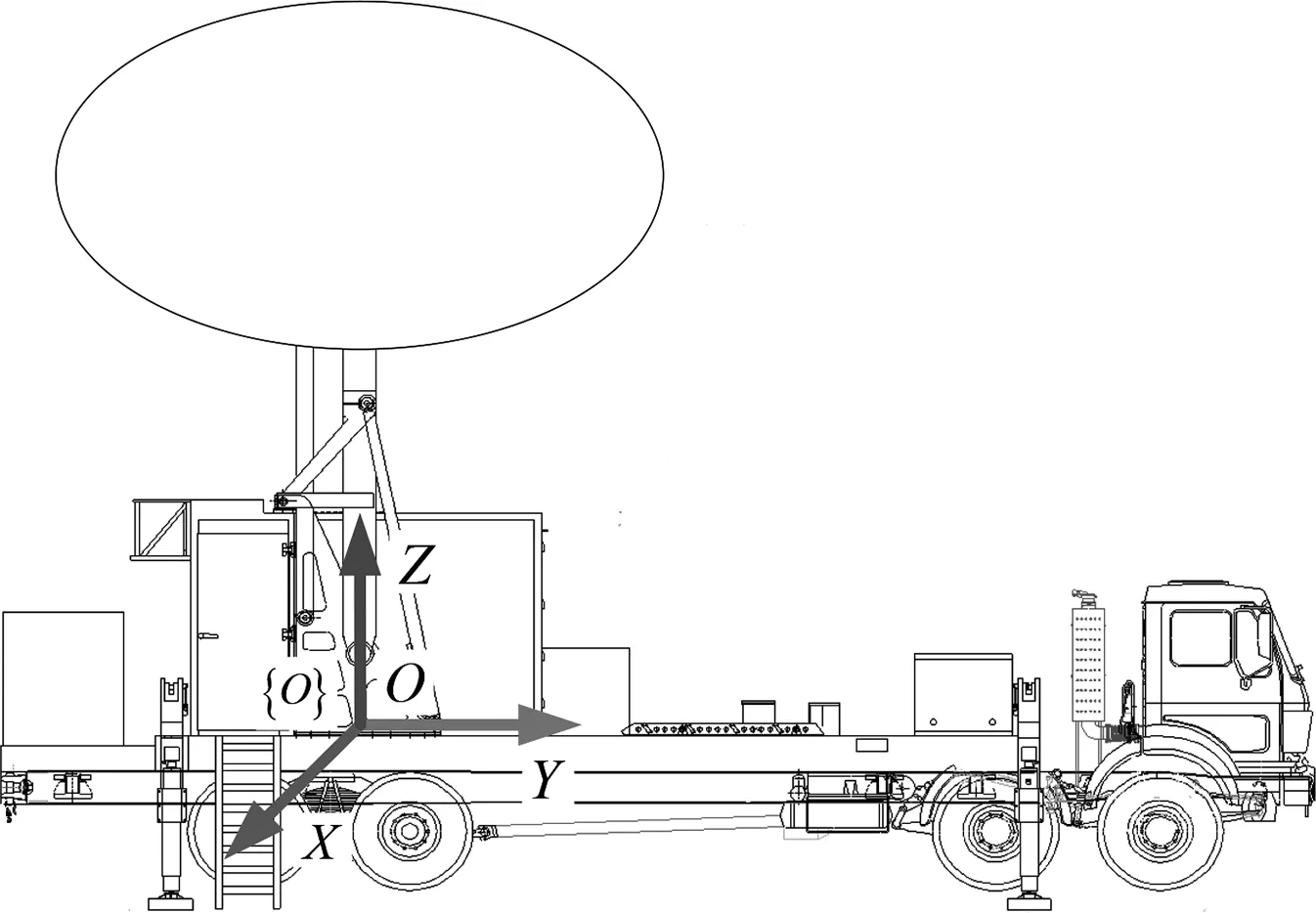
图1 天线机动车简化结构图

车载平台的简化模型如图2所示。设大地坐标系为{Og},分别建立车载平台在天线收叠和架设状态下的坐标系。在天线收叠状态下,车载平台的坐标系为{O},原点O为倾角传感器中心,OXY平面与车载平台重合,OY轴指向车首,Z轴垂直于车载平台向上,X轴与Y轴、Z轴形成右手坐标系。在天线架设状态下,车载平台的坐标系为{M},原点M为倾角传感器中心,MX′Y′与车载平台重合,MY′轴指向车首,Z′轴垂直于车载平台向上,X′轴与Y′轴、Z′轴形成右手坐标系。

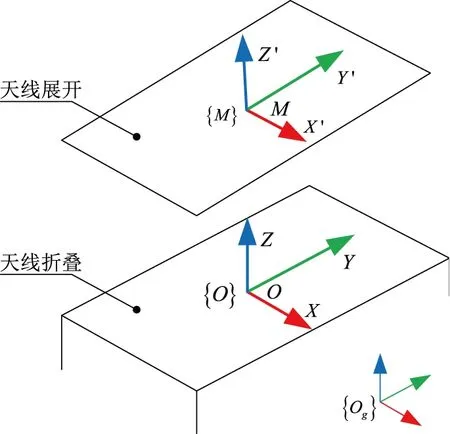
图2 车载平台简化模型

2 偏移姿态分析

车载平台的倾角传感器采用卡尔丹环架结构,其姿态测量原理为先绕Y轴旋转,再绕X轴旋转的变换顺序进行[3]。当车载平台调平完成时,设传感器的值为δx和δy,此时车载平台坐标系{O}相对于大地坐标系{Og}的姿态为Rδ,则其变换关系满足

(1)

当天线架设后,车载平台的重心发生变化,对其姿态产生的影响为Rθ,设其绕X轴、Y轴和Z轴旋转角度分别为θx、θy和θz,满足

(2)

此时,传感器的值为ρx、ρy,车载平台坐标系{M}相对于大地坐标系{Og}的姿态为Rρ,另设坐标系{M}绕Z轴旋转角度为ρz,则其变换关系满足

(3)

可得Rδ、Rθ和Rρ三者之间的姿态变换关系满足

(4)

则Rθ可表示为

(5)

展开后可得

(6)

根据实际情况,可知θx、θy满足θx,θy∈(-π/2,π/2),则整理后可得

(7)

由于车载平台调平完成后,即使车载平台的重心产生变化,4条调平蛙腿的位置也基本不动,所以车载平台绕Z轴旋转的角度θz和ρz都很小。在本系统中,θz和ρz为不可控量,且其与调平没有关系,这里不作考虑。根据实际车载调平情况,可知δx、δy、θx、θy、ρx和ρy都是小角度,其值均不大于5′,则近似整理后可得

(8)

在坐标系{Og}、{O}和{M}的变换过程中,由于YXZ变换与ZYZ变换具有等效关系,设ZYZ变换角分别为αi、βi、γi(i=δ,θ,ρ),可得到Rδ、Rθ和Rρ的最大倾角满足

(9)

式中,βδ为天线在收叠状态下车载平台的调平误差倾角,βρ为天线在架设状态下车载平台的调平误差倾角,βθ为车载平台重心偏移引起的最大倾角。

3 误差补偿方法

在天线架设状态下,为了使车载平台处于水平状态,即ρx=ρy=0,需要保证初始调平姿态误差Rδ与重心偏移引起的姿态变化Rθ相互抵消,则满足

(10)

在调平过程中,由于地域、温度、初始状态等条件的影响,车载平台每次调平都存在差异,即每次计算得到的θx和θy值都不同。因此,需要设计相应的算法,能够根据车载平台的工作条件动态更新重心偏移引起的姿态变化θx和θy。

误差补偿迭代算法如图3所示。设Pδ=[δxδy]T、Pθ=[θxθy]T、Pρ=[ρxρy]T。首先读取上一次存储的重心偏移姿态Pθ和Cθ,如果是首次迭代,Pθ和Cθ的初始值可令为0。车载平台调平的最终目标设为Pδ=- Pθ,调平完成后,用此时传感器的测量值更新Pδ。天线架设后,记录传感器的测量值为Pρ,计算Pθ=Pρ- Pδ。最后,通过卡尔曼滤波器对Pθ进行滤波处理并存储。至此,车载平台完成了一次迭代,存储的Pθ和Cθ用于下次调平迭代。

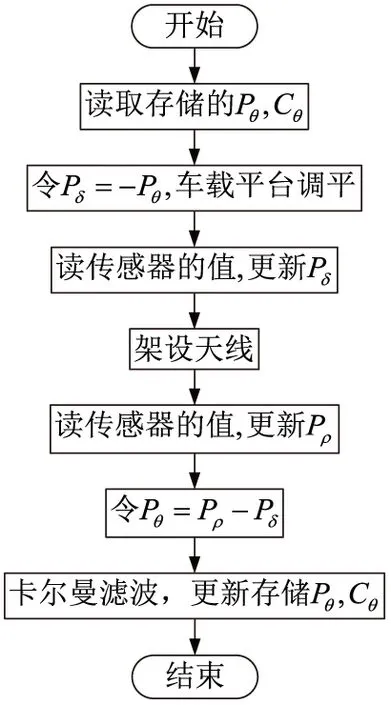
图3 误差补偿迭代算法

在车载平台迭代调平过程中,为了减小传感器测量误差和外界环境干扰等因素对调平精度和稳定性的影响,系统引入卡尔曼滤波器对计算得到的Pθ进行滤波处理[4]。

卡尔曼滤波器状态估计方程:

(11)

式中,Pθ(k-1|k-1)为上一状态卡尔曼滤波器的状态修正结果,即本系统中上一次存储的Pθ;U (k)为系统输入,本系统中,U(k)=0,A=B=1。

卡尔曼滤波器协方差估计方程:

(12)

式中,Cθ(k-1|k-1)为上一状态卡尔曼滤波器的协方差修正结果;AT为A的转置矩阵;W为系统过程噪声,本系统中,W=1角分2。

卡尔曼滤波器状态修正方程:

(13)

式中,Z (k)为状态观测器,即本系统中的传感器测量值;Kg(k)为卡尔曼滤波器增益;本系统中,H=1。

卡尔曼滤波器增益:

(14)

式中,V为系统测量噪声,本系统中,V=3角分2。

卡尔曼滤波器协方差修正方程:

(15)

式中,I为单位矩阵,本系统中,I=1。

通过以上5个方程,可以对每次的Pθ进行滤波处理,提高系统的测量精度。

4 实验验证

将设计的误差补偿方法代入车载平台的调平控制系统,并对车载平台和天线进行多次调平和架设。令Pθ和Cθ的初始值为0,分析卡尔曼滤波器对Pθ的滤波效果。待Pθ值稳定后,分析该误差补偿方法对车载平台调平效果的影响。

卡尔曼滤波器对θx和θy的滤波效果分别如图4和图5所示。经过卡尔曼滤波后,可以有效抑制噪声对θx和θy的影响,增强了系统的鲁棒性。随着迭代次数,θx和θy的值能够快速收敛,且收敛值与其初始值无关。

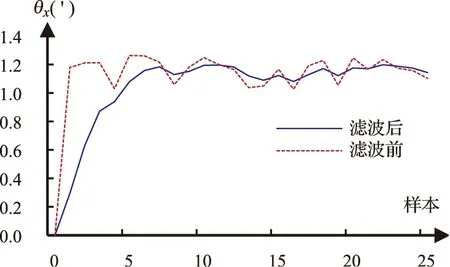
图4 θx卡尔曼滤波前后比较

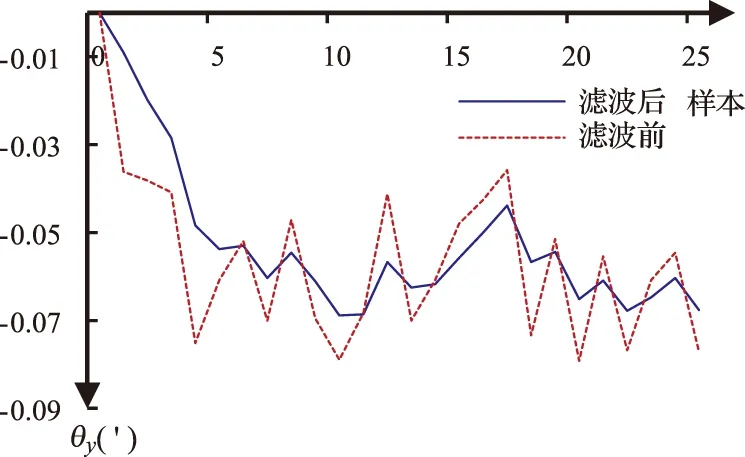
图5 θy卡尔曼滤波前后比较

图6 X轴调平误差补偿前后比较

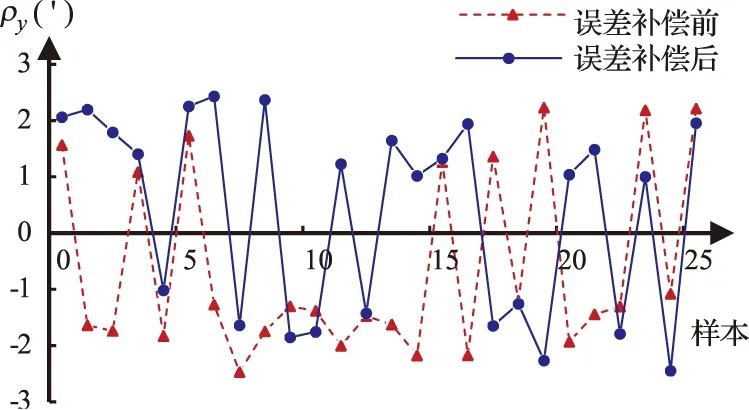
图7 Y轴调平误差补偿前后比较

该误差补偿方法对车载平台重心偏移引起的调平误差补偿效果Pρ如图6和图7所示。由图可以看出,该误差补偿方法对ρx的补偿效果(图6)要比对ρy的补偿效果(图7)较为明显。分析原因可知,在天线收叠和架设过程中,车载平台的重心主要沿Y轴方向偏移,沿X轴方向偏移较小。因此,车载平台重心引起的姿态偏差主要绕X轴,即对ρx的补偿效果更为明显。

利用ρx和ρy计算出车载平台的最大倾角βρ,如图8所示。βρ在补偿前的均值为2.05′,补偿后的均值降为1.71′。实验证明,该误差补偿方法对车载平台重心偏移引起的位姿误差有一定的补偿效果。比较图6和图8可以看出,该误差补偿方法对βρ的补偿效果比对ρx的补偿效果有所减弱。这主要是由于车载平台对ρy的调节精度较低(图7),仅能达到±2.5′。如果能够适当提高对车载平台ρy的调节精度,该误差补偿方法对βρ的补偿效果会更加明显。

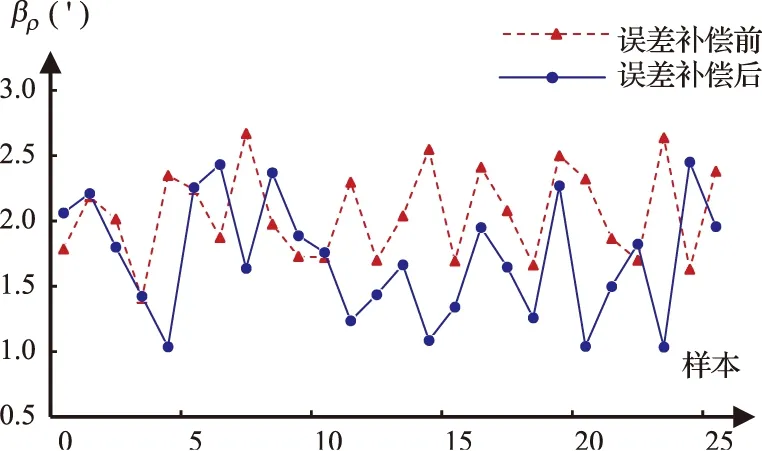
图8 综合调平误差补偿前后比较

5 结束语

针对车载平台重心偏移引起的姿态误差,本文建立了姿态误差的数学模型及工程简化模型,设计了相应的误差补偿方法。利用卡尔曼滤波器对车载平台重心偏移引起的姿态误差进行滤波,有效降低了外界干扰对Pθ的影响。通过实验对设计的误差补偿方法进行验证,实验结果证明该方法能够有效补偿车载平台重心偏移引起的调平误差。

在天线机动车工作过程中,由于天线转动、风速和风向等因素的影响,天线的水平姿态会产生动态变化,这在一定程度上也会影响天线的测量精度。在这种情况下，采用机械调整对姿态偏差进行实时补偿难以实现,可以考虑利用天线姿态的实时测量值,通过相应的算法对天线的探测倾角进行修正。

[1] 冯仪,陈柏金.车载雷达机电式自动调平控制系统[J].华中科技大学学报(自然科学版),2004,32(6):66-71.

[2] 李迪科,李萍,等.某雷达自动电调平控制系统的设计[J].重庆大学学报,2004,27(6):93-95.

[3] 刘延柱.关于刚体姿态的数学表达[J].力学与实践,2008(1):99-101.

[4] 张强,孙尧,等.多普勒测速声纳的自适应Kalman滤波算法[J].哈尔滨工程大学学报，2011,32(12):1534-1538.

A compensation method of leveling error causedby center-of-gravity shift of vehicle-borne platform

MA Tong1, REN Xue-feng2, ZHOU Hong1, SONG Rong-gui1

(1. No. 724 Research Institute of CSIC, Nanjing 211153；2. Military Representatives Office of Radar System of the PLA Navy in Nanjing, Nanjing 210003)

The attitude change caused by the center-of-gravity shift of the vehicle-borne platform is analyzed, and the mathematical model of the attitude error is built through the YXZ transformation and then simplified according to the practical engineering. Based on the attitude error model, a compensation method of the leveling error of the vehicle-borne platform is designed. Besides, the system filters the attitude error with the Kalman filter. The test results indicate that the method can effectively compensate the leveling error caused by the center-of-gravity shift of the vehicle-borne platform.

vehicle-borne radar; vehicle-borne platform; vehicle-borne antenna; center-of-gravity shift; error compensation; YXZ transformation; attitude error

2016-10-20;

2016-11-03

马同(1989-),男,助理工程师,硕士,研究方向:伺服控制系统设计;任雪峰(1986-)，男，工程师，研究方向：质量管理；周泓(1970-),女,工程师,研究方向:机电一体化设计;宋荣贵(1984-),工程师,硕士,研究方向:雷达系统结构设计

TN959.71

A

1009-0401(2017)01-0048-04