一种曲线路径剪裁中刀具形变及其误差分析

张新星，杨 帆,2

(1.衢州职业技术学院，浙江 衢州 324000; 2.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州 310014)

一种曲线路径剪裁中刀具形变及其误差分析

张新星1，杨 帆1,2

(1.衢州职业技术学院，浙江 衢州 324000; 2.浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州 310014)

动态移动切削阻力载荷对高速数控裁床加工过程中刀具形变及其剪裁误差具有的重要影响，提出了一种适用多层布料/皮革曲线剪裁路径的刀具形变及其误差计算方法;建立了动态负载条件下可伸缩刀具的挠度与转角方程，进而推导出高频振动裁刀剪裁误差及其随切削深度变化规律;计算结果表明，数控布料/皮革剪裁刀的动态载荷、高频振动参数、切削深度对剪裁误差具有重要影响，深入剖析高层数控裁床的加工机理，动态参数数据分析，对于提高机床加工效率，降低加工误差，提高刀具使用寿命具有一定的工程应用价值。

高层数控裁床；曲线路径；动态载荷；刀具弹性形变；误差

0 前言

高层数控裁床与通用数控装备比较，有3个显著特征：裁床主运动为高频振动运动；高层数控裁床的加工刀具为薄片状结构，某一方向刚度相对较大，另一正交方向刚度相对较小；被加工对象为“薄片状”大面积非金属材料，诸如皮革、布料、塑料等，如图1，图2所示[1-2]。高层数控裁床在剪裁布料/皮革等过程中，刀具及其加持杆沿着刚度较大的导轨伸出量是间歇振动变化；进给速度大，剪裁对象强度相对较大，尤其剪裁路径为曲线的条件下，刀具变形严重，造成高层剪裁对象上下剪裁误差较大，插补精度高低已经失去作用，故对变截面、伸缩动态变化的刀具变形及其剪裁误差进行研究。国内学者在数控裁剪系统理论这一狭窄研究领域起步较晚，在动力学方面做了一定的研究工作。

太原理工大学李元斌团队重点研究了数控裁床的进给系统结构设计及其动态仿真研究，采用分段建模，并对其做动力学仿真[3]；运动simulink设计了闭环PID机电控制系统，联合动力学ADAMS联合仿真，验证了控制参数的合理性。浙江工业大学赵燕伟团队在多层鞋革高速智能裁割系统与装置研制方面进行了较详尽的研究[4]，在高层数控裁床的机构系统上，对刀头系统、进给系统建立了三维模型，通过ADAMS对其动力学仿真和优化，获得了良好的结构参数和动力参数，并对主运动系统和进给系统进行了动力学仿真和多目标优化，为提高剪裁效率提供了有力的理论支撑。

图1 裁刀主高频振动系统

图2 数控裁刀片

动态载荷及其形变等研究领域，国内学者做了大量的工作和试验探索。湖南大学汽车国家重点实验室提出一种时域内多元动态载荷反求计算方法[5]，运用一些系列的脉冲或者阶跃函数表示系统响应函数，对动力响应的卷积进行离散，并通过滤波技术、正则化方法和优化策略，重构多源动态载荷，有效地获取载荷近似值。西南交通大学牵引动力国家重点实验室马卫华等提出了轮轴弯曲刚度对垂向动态载荷的影响研究方法[6]，通过采用刚性和弹性轮对模型建立在动态载荷下的动力学分析模型，对比分析出弯曲度对于垂直载荷的影响，实现改善轮轨动态接触状态的目的。浙江大学吕永桂博士等对空间柔性构件弯扭耦合振动进行了研究[7]，通过拉格朗日方程和假设模态法计算出柔性体的动力学方程，运用一种Lyapunov速度反馈控制算法抑制了振动位移，实验效果明显。同校学者颜潇潇等对复杂载荷下梁柱翘曲传递进行分析，分析了节点处双力矩和翘曲自由度的关系，提出了基于模型与板壳有限元方法，实验结果表明该方法提高了复杂载荷下形变的理论计算精度[8]。同校周磊博士提出了一种翘曲变形矫正模型，该模型以导轨的初始翘曲挠度为依据，准确而快速地计算出相应的矫正行程[9]。借鉴前人理论方法研究成果，动态载荷条件下引起形变的因素及其相互耦合关系，本文针对高层数控裁床裁刀剪裁加工过程中进行弹性形变分析，并对刀具弹性形变下切削误差进行研究。

1 曲线剪裁动态载荷及形变

曲线路径剪裁过程与直线剪裁明显不同，裁刀不仅受正面剪裁阻力，也受到因动态实时相切角度插补而产生的扭矩，数控裁刀的片状刀具受扭转变形一定影响剪裁精度，大大降低了刀具剪裁效率；数控剪裁是采用高速振动刀具进行材料加工的，作用在刀具上的负载作用点实时发生变化，这也是数控剪裁加工过程中刀具受力有所不同的显著特征。故必要对其进行深入的分析和研究，对曲线刀具变形及其误差进行探讨。

如图3所示，假设刀头机构中加持杆以上限位结构具有足够的刚度，即不会发生形变，刀具加持杆相对于刀头机构而言，只有两个自由度：沿着导套高频振动，能通过伺服电机完成顶刀轮完成旋转。高频振动刀具的运动规律公式为：

图3 皮革剪裁刀的受力情况

(1)

其中:T1为刀具弹性模量矩阵，T2为刀具载荷下形变矩阵，T3为刀具载荷矩阵。根据形变与载荷关系则有：

(1)

对于公式(2)进行整理化成方程式：

(2)

根据弹性形变理论，对高频振动裁刀及其加持杆进行线性载荷形变分析，求得：

(3)

其中:公式中Mx1=-qx·L·(H0+L/2)，My1=-qy·L·(H0+L/2)。根据受力及其变形分析，刀具弯矩挠度计算不可以运用相对运动的方式进行推导：以为刀杆深入滑轨之内，滑轨刚度很大，可以假设其不变形，因此可以把刀具滑轨端看做是固定端进行研究，载荷作用位置和大小不变，加持杆及其夹持刀具根据时间不同伸缩，从而直接影响弯矩值和挠度；在扭矩的作用下，刀具扭转角度不受导轨限制，也不存在刀具刃口切偏的问题，因为扭转角度都在XOY平面内，不需正交分析。你导轨内部也要计算在内；刀具加持杆扭转角与刀具扭转角是可以直接累加的，首先列出扭转角与转矩的公式：

(4)

根据图所示，求得：

(5)

设刀具加持杆部分的长度为H0，则受扭转变形影响的部分长度是动态变化的，其长度为H00=H0+R0sinωt，最长伸出量为H0+R0，最小伸出量为H0+R0(H0≥R0)，其中R0曲柄滑块机构回转半径。为了研究方便，假设与加持杆连接的部分与加持杆几何参数与力学参数一致。对于公式(4)进行二次积分，即:

(6)

式中,L0为剪裁皮革；Ip1为刀具加持杆的极性惯性矩，R为刀补半径，即裁刀宽度的一半。刀具部分分成两部分进行分析，前部分为在某一时刻t0时刻在剪裁对象外部的部分，后部分为与剪裁对象接触部分，独立分析研究。设总是在剪裁对象部分H11=H1+R0sinωt，刀具的极惯性矩为Ip2，刀具最长伸出量为H1+R0，最小伸出量为H1-R0(H0≥R0)，补充说明H1与R0非常接近，减少刀具变形量，降低刀具剪裁误差。参照(6)公式，得出时刻在剪裁对象外部的扭转变形角为：

(7)

对于刀具在剪裁对象内部部分，两次积分的上下限不同，如下所示：

(8)

将公式(6)、(7)、(8)联合起来，三部分转角进行叠加，总扭转角为：

(9)

图4 裁刀截面上扭矩受力分析

根据刀具变形前后变形位置变化图示5所示，A0→A1→A2可以推导出如下公式，设A0(x0，y0)，A1(x1，y1)，A2(x2，y2)，最大剪裁误差Δε：

图5 剪裁刀具变形前后位置变化

(10)

(11)

剪裁布料/皮革材料过程中，刀具剪裁曲线过程中的形变影响相邻的不同排样剪裁误差，如图6所示。设加工余量为ΔE，O1O2为剪裁预期位置。刀具补偿误差计算公式：

Δε0=(Δε1+Δε2)/2

(12)

Δεi可以通过(11)公式可以求出，并且满足|Δε2-Δε1|≤2ΔE，通过控制最小剪裁余量，防止剪裁超差，出现报废样品。由此可以得出结论：精确的排样和路径优化、优良的插补算法与裁刀形变分析及刀具补偿方法联合研究，才能保证剪裁误差在有效控制范围。

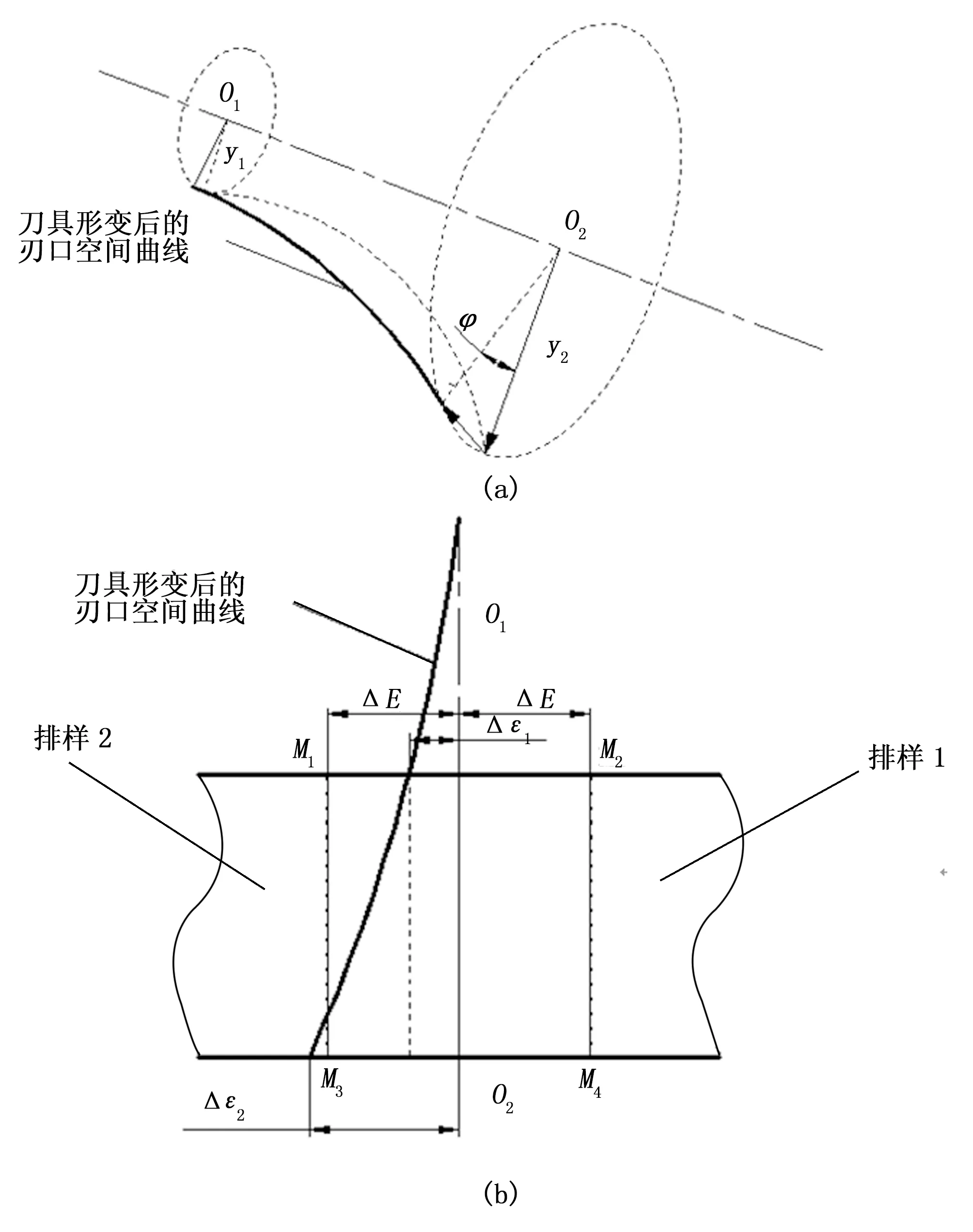
图6 剪裁刀具变形前后位置变化

2 裁刀的惯性矩与极惯性矩

不同于直线剪裁过程中载荷单一，曲线剪裁，刀具必然受扭矩作用，切向方向受剪裁阻力作用。刀具在多方载荷的作用下产生弯、扭变形甚至翘曲的可能，故有必要根据推导的理论对曲线加工过程中的形变误差进一步研究和仿真分析。直线路径剪裁，采用积分法求出刀具截面几何特性参数，工程上使用较少，学院派使用较多。工程上对于较规则图形，采用(13)公式当时进行求解惯性矩与极性惯性矩。首先根据数控裁刀截面的几何性质，如图7所示，求出数控裁刀与加持杆的惯性矩及其极惯性矩，有下列公式成立：

图7 刀具截面形状及其惯性矩分析

(13)

(14)

(15)

(16)

如图7所示，对于刀具对X、Y轴的惯性矩推导：

(17)

式中,I1x，I2x，I3x是对于Y轴的3种类型截面的惯性矩；I1y，I2y，I3y是对于X轴的3种类型截面的惯性矩。

(18)

式中,I1x，I2x，I3x是各个类型截面对经过刀具形心，与Y平行轴的惯性矩； 是各个类型截面本身的惯性矩；a1，a2，a3为各个类型截面形心距离刀具截面形心之距离，A1，A2，A3分别为刀背半圆弧面积、刀身主截面矩形面积和刃口截面三角形面积。

(19)

(20)

(21)

刀具加持杆截面为圆形，直接求得惯性矩和极性惯性矩为：

(22)

3 工程数据分析

某高层数控裁床的刀具高频振动设计参数曲柄半径R=25 mm，驱动电机转速最高转速ω=2 400 rad/min，剪裁刀的夹持杆直径d=12 mm，剪裁刀总宽度H1=8 mm，剪裁刀切削刃口两侧楔面夹角β=20°，剪裁刀厚度δ=2.5 mm，剪裁对象厚度L=100 mm，预设剪裁均布载荷q(v)=2.0 N/mm。首先对数控剪裁刀柄的挠度、转角数据、动态剪裁面积变化等进行分析。

图8 变载荷条件下刀具扭转角变化

图示8显示，在剪裁其他条件不变的情况下，调整剪裁载荷，则曲线插补扭转角度增大；同一时刻，切削深度越大，扭转角越大；同一深度，随着时间不同，角度周期性变化；调整仿真时间和深度步长，扭转深度显著增加。

图示9显示，在剪裁其他条件不变的情况下，调整剪裁载荷，则曲线剪裁误差也相应变化；同一时刻，切削深度越大，

图9 变曲率条件下刀具扭转角变化

剪裁误差越大；同一深度，随着时间不同，剪裁误差周期性变化；高层数控裁床高频振动幅度越大，剪裁误差也显著增加。

4 结论

为了分析高层数控裁床在曲线路径剪裁中，载荷变化、高频振动参数、切削深度对裁刀形变及其剪裁误差影响程度问题，建立了剪裁刀具动态载荷数学模型，刀具形变误差模型，提出了刀具形变计算方法及其误差补偿方法。

(1)建立了刀具夹持杆和刀具一体的悬臂长度随时间变化的梁挠度和扭转角数学方程，并推导了刀具不规则截面的静矩和惯性矩方程。

(2)建立了基于刀具挠度变化的补偿误差数学方程。

(3)在高层数控裁床的移动载荷基础上，分析了载荷变化、高频振动幅度、切削深度对刀具形变及其误差周期性变化规律，为高层数控裁床插补技术和刀具补偿方法提供重要理论依据，具有一定的工程实用价值。

[1] 金爱燕,高佩佩,尚笑梅. 针对成衣样版特征的裁剪路径优化设计[J]. 纺织学报,2015(9):89-93.

[2] 项贤军,茹秋生. 裁床裁剪复杂形状速度控制研究[J]. 制造业自动化,2014(9):56-58+67.

[3] 王 雷，李文斌. 数控裁剪机伺服进给系统动态联合仿真[J].制造业自动化，2013(8):139-141.

[4] 盛 猛. 多层皮革高速裁剪机伺服进给系统多目标优化[D].杭州：浙江工业大学，2012.

[5] 伍乾坤，韩 旭，胡德安. 一种脆性材料动态本构损伤参数的计算反求方法[J]. 固体力学学报，2011(3):242-248.

[6] 马卫华，宋荣荣，揭长安等. 缓冲器阻抗特性对重载列车动力学性能的影响[J]. 交通运输工程学报，2011(2):59-64.

[7] 吕永桂，魏燕定，陈子辰. 空间两连杆柔性构件弯扭耦合振动主动控制[J]. 浙江大学学报(工学版)，2007(5):715-719.

[8] 颜潇潇，童根树，张 磊. 斜加劲梁柱节点翘曲传递分析[J]. 浙江大学学报(工学版)，2006(1):85-91.

[9] 周 磊，罗禹贡，杨殿阁,等. 混联式混合动力车多能源动力控制系统的开发[J]. 机械工程学报，2007(4):125-131.

Tool Deformation and its Error Analysis in Curve Path Clipping

Zhang Xinxing1,Yang Fan1,2

(1.QuZhou College of Technology,QuZhou 324000,China;2.Zhejiang University of Technology Key Laboratory of E&M,Hangzhou 310014,China)

Dynamic cutting resistance of moving load is an important factor affecting the tool deformation during operation of high-layer CNC cutting machine. A tool deformation and error calculation method that is suitable to the multi-layer clothing/leather cutting in curve path was proposed. And deflection and rotating angle equation were established under the condition of dynamic load, and thus we can deduce the cutting error of the machine tool with high-frequency vibration and its change rule correlated with cutting depth. The calculation result reveals that factors of dynamic load, High frequency vibration parameters, and cutting depth have strong influence on the cutting error. Deeply research on machining mechanism and dynamic parameters analysis of the high-layer CNC cutting machine has certain engineering application value in improving work efficiency, reducing machining error, and prolonging service life of cutting tools.

High-layer CNC cutting machine; curve path; dynamic load; elastic deformation; error

2016-05-19；

2017-01-09。

国家自然科学基金项目(52575477)；浙江省重大科技专项项目(2009C11039)；浙江省教育厅高校访问学者(境外培训项目)教师专业发展项目(ZF2015147)。

张新星(1982-)，男，浙江衢州人，讲师。主要从事数字化控制技术方向的研究。

1671-4598(2017)03-0150-05DOI：10.16526/j.cnki.11-4762/tp

TP

A