海岛界定数量的变维分形特征——以嵊泗县为例
王欣凯, 夏小明, 程 林
海岛界定数量的变维分形特征——以嵊泗县为例
王欣凯1, 2, 夏小明2, 程 林3
(1. 浙江大学 地球科学学院, 浙江 杭州 310012; 2. 国家海洋局第二海洋研究所 杭州 310012; 3. 河北省科学院地理科学研究所, 河北 石家庄 050051)
我国多次海岛数量普查因界定标准不一而结果相差巨大, 为了满足海洋主管部门对海岛的管理要求, 亟需研究合理的方法界定海岛数量。利用高分辨率遥感影像解译嵊泗县海岛2 875个, 以分形理论讨论海岛数量与海岛面积、海岛间距的关联。结果表明, 嵊泗县50%的海岛面积小于50 m2或岛间距不足6 m, 海岛数量与界定标准间呈分维数先增大后稳定的变维分形特征, 分维数在220 m2和28.5 m之后稳定在1.80和2.25。以200~500 m2为界区分大小岛, 小岛数量和海岛间距也存在变维分形特征, 且分维数在间距大于50 m后趋于稳定。故嵊泗海岛最佳界定方法为以220 m2筛选出计数海岛后再补充间距大于50 m的较小海岛, 该方法下界定嵊泗海岛681个。
海岛数量; 海岛面积; 海岛间距; 变维分形
我国是海洋大国, 沿海密布海岛, 然而海岛数量却在数次全国性海岛普查项目中相去甚远。例如: 1976年, 确认我国海岛6 536个; 20世纪80年代末, 确认我国不含港、澳、台地区的海岛6 971个[1]; 最新一轮的“908专项”调查, 确认我国海岛10 312个[2]。除客观的海岛灭失及新岛被发现外, 海岛界定方法的不同是主要原因。当前我国海岛数量的界定方法主要依据海岛面积和海岛间距两个界定参数, 界定参数取值越精细统计所得海岛数量越多。该特征类似于Mandelbrot提出的分形, 分形理论起源于对地学形态的研究, 其指出分形集中对象的测量结果随所用尺度变化而不同, 并利用分维数来描述此类变化特征[3]。以往对分形特征的研究, 多集中于有具体形态的对象, 如岸线、地形等。那么海岛数量这一抽象对象是否也与界定参数构成分形特征?本文由此入手, 以浙江嵊泗县海岛为例, 利用浙江省航空摄影测量成果获取嵊泗县可识别海岛的地理信息, 依据海岛数量和界定参数之间的数量关系讨论其分形特征, 并提出了依靠分维数变化规律界定海岛数量的方法。本文将分形理论推广到了抽象对象, 研究结果为我国海岛数量的管理提出了科学的参考依据。
1 数据与方法
1.1 海岛岸线提取
本文的研究区域嵊泗海域位于东海的杭州湾外侧,所辖海岛众多且距大陆较远(图1), 海岸线人类活动较少干预, 多处于自然状态。本文依托“浙江908专项”海岛岸线专题的成果, 参考2007—2008年的航空遥感影像, 通过人工解译的方法提取嵊泗县所有可判识海岛的岸线信息。所用影像主要源于2008年拍摄的地面分辨率0.8 m的浙江省沿海低潮时航空摄影成果, 并以Google Earth Pro软件截取的拍摄时间为2007年3—7月的地面分辨率0.5~0.7 m的影像作为补充。
海岸线为大潮高潮位时海面所淹没的水陆界线[4], 由于所用影像中的潮时各异, 故本文参考国家海洋局所编规程和前人的研究[4-6], 依靠高空间分辨率影像的优势, 从海岸线的野外地貌特征进行判识解译。即人工型海岸线位置位于人工构筑物的外缘, 基岩型和沙砾质岸线的位置位于岩石和沙滩上颜色由深到浅的分界线。利用ArcGIS 软件将所用影像和提取岸线统一到CGCS2000坐标系并以121°E中央经线进行高斯-克吕格投影, 再对海岛面积、间距等各类地理信息进行计算。
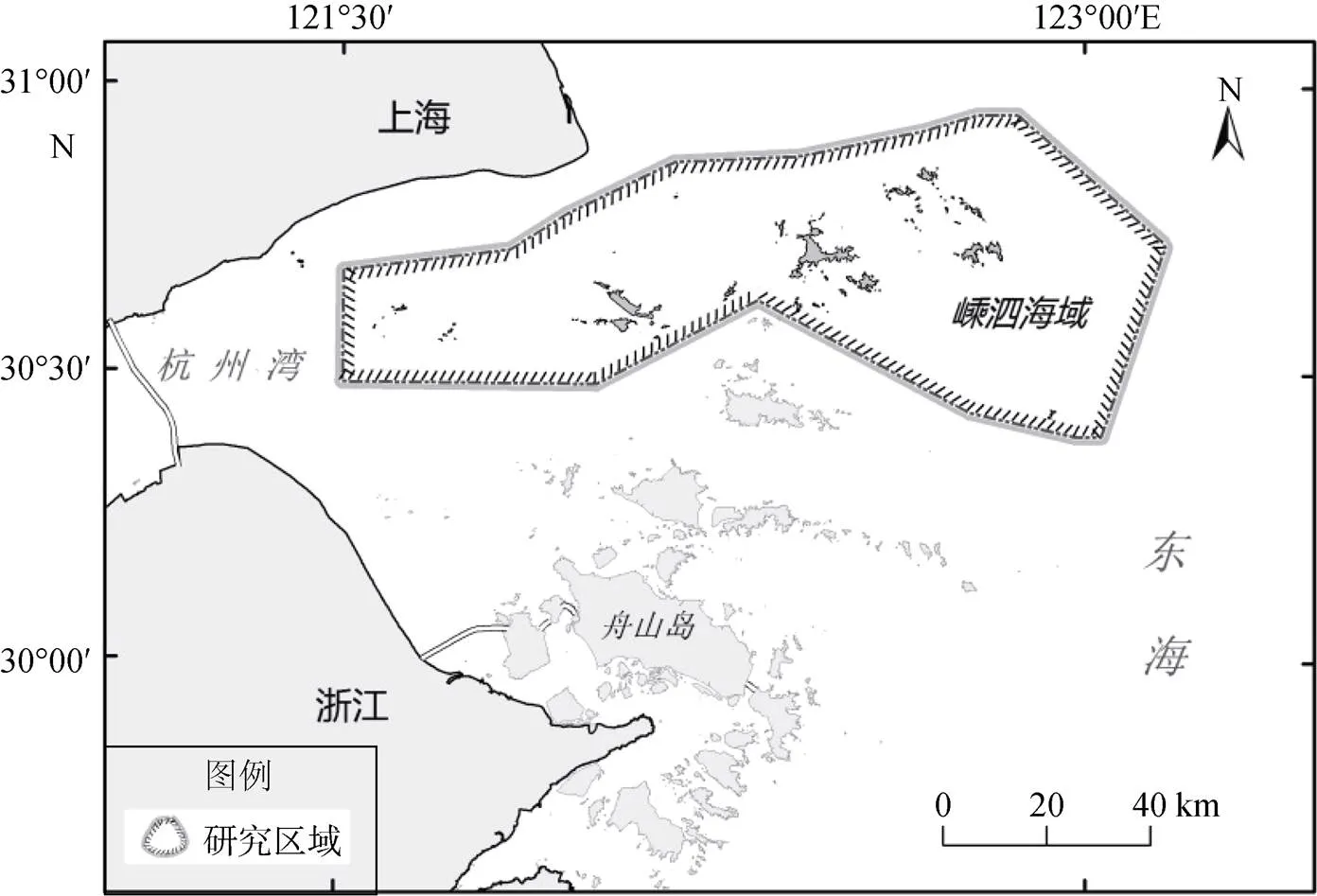
图1 研究区域简图
1.2 海岛数量的统计方法

1.3 分形特征研究方法
分形理论指出, 分形对象的测量结果随所用尺度呈指数变化[3], 并满足式(1)中所示关系。
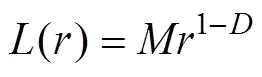
式中:()为被测对象结果,为测量尺度,为待定常数,为被测对象分维数。对式(1)两边同时取对数, 可得:

即理想状态下, 具有分析特征对象的测量结果和尺度将在双对数坐标系中投射出一条直线, 且斜率与分维数相关。本文将界定参数和取值对应为测量尺度, 相应海岛数量N和N对应为测量结果(), 同样将结果绘制于双对数坐标系中分析海岛数量的变化趋势。同时依界定参数升序, 将前30个数据点作为基础样本, 利用最小二乘法计算样本的分维数, 随后逐个将下一数据点加入样本空间计算分维数, 至样本包含全部数据点。分析上述所得与界定参数相关的分维数序列, 研究海岛数量的分形特征。
2 结果
2.1 嵊泗海岛数量概况
本文共识别嵊泗县海岛2 875个, 相比于“浙江908专项”的508个[2], 海岛数量增至5.6倍。其中面积大于4 m2的海岛2 113个, 最大的为泗礁山岛的22.6 km2; 海岛间距大于2 m的海岛2 586个, 最远的为半洋礁的3.9 km。> 2的海岛中52.6%位于<7的区间里,<100区间中的海岛占94.4%。以2个单位为步长放大<100的区间(图2), 在∈(2, 4)时海岛数量的分布密度最大, 为443个。随着增大, 海岛数量的分布密度迅速减小, 至=20附近时减小趋势停止, 并大致在∈(20, 34)的区间内稳定在25附近。当>34时, 海岛数量的分布密度进一步减小至零星分布。
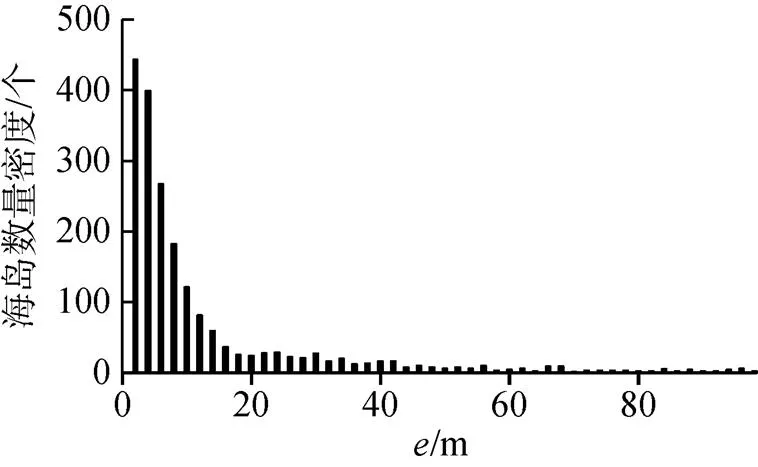
图2 基于面积的海岛数量密度分布
海岛间距方面的分布情况与之类似,>2的海岛中55.8%位于<6的区间里,<35区间中的海岛占98%。以1个单位为步长放大<35的区间(图3), 在∈(2, 3)时海岛数量的分布密度最大, 为447个。随着增大, 海岛数量的分布密度迅速减小, 至=20附近时, 减小的速率明显降低, 随后进一步减小至零星分布。
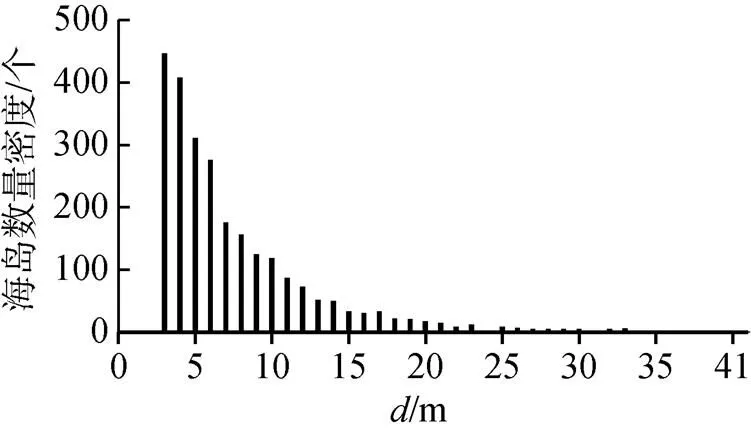
图3 基于间距的海岛数量密度分布
2.2 海岛数量的分形特征
依据海岛数量的统计结果, 从海岛面积和海岛间距两个方面, 将界定值和与相应海岛数量的自然对数绘制成图4。图4显示随着界定参数值增大, 界定的海岛数量迅速减小。两条曲线形状和变化趋势大致相同, 但海岛面积所示图像直线相关性更好, 斜率变化不大, 而海岛间距所指示图像直线相关性稍差, 斜率有着明显的先变陡再变缓过程。

图4 海岛数量与界定参数的双对数关系
依据本文构建的海岛面积和海岛间距两个样本组, 以样本组中每个样本空间内和最大值的自然对数为横坐标, 样本分维数为纵坐标绘制曲线(图5)。图5显示代表海岛面积和海岛间距的ln和ln两条曲线都表现出分维数先增大后迅速趋于平稳的变维分形特征。在海岛面积方面, 拐点为ln=2.69, 对应海岛面积为220 m2。2<220 m2时, 样本分维数从1.25逐渐增大至1.70;2>220 m2时, 样本分维数稳定于1.70至1.80之间, 全样本分维数为1.80。在海岛间距方面, 拐点为ln=3.35, 对应海岛间距为28.5 m。即<28.5 m时, 分维数从1.35逐渐增大至2.25; 当>28.5 m时, 样本分维数稳定于2.25附近, 全样本分维数为2.25。

图5 海岛数量的分维数与界定参数的关系
对比该两条曲线, 初始阶段海岛间距样本的分维数比海岛面积的约大0.25, 两者分维数增大的速率相近, 接着海岛面积方面分维数稳定, 海岛间距方面分维数继续增大, 两组分维数都稳定后, 海岛间距的分维数比海岛面积约大0.5。
3 讨论
3.1 变维分形特征及其意义
依据本文计算结果, 海岛数量在海岛面积和海岛间距两方面都存在着明显的分形特征, 但分维数在所研究的尺度范围内并非一直稳定, 而是存在着先增大后稳定的过程。汪富泉等[8]在研究大自然事物的分形特征时也发现了类似现象, 分维数在一段尺度区间内时是稳定的, 但超过该区间后分维数将明显变化。本文将这种分维数随尺度范围不同而发生改变的特征称为变维分形特征。由于同类特征的分维数相似, 异类特征的分维数不同[9-10]。本文推断分维数随尺度变化的原因在于不同尺度下事物的特征发生了改变。这种现象在自然界中是存在的, 如图6所示, 沙滩表面在米级的尺度下可视作平面, 放大到毫米级尺度则是延绵起伏曲面, 放大到微米尺度则脱离二维属性表现离散特征。在描述沙滩面积时, 以上三个尺度下的对象特征和分维数显然都会差异巨大, 表现出变维分形特征。
变维分形特征在分维数变化的同时又包含了分维数的稳定部分。正如本文海岛数量的分维数, 在中后段也是稳定的, 拥有一致的分形特征。本文将分维数稳定的区间称为该分形特征的特征区间。在特征区间内所有尺度描述的对象特征是一致的, 结果随尺度的变化可由分维数推算, 属量变范畴。尺度越过特征区间, 分维数发生改变, 该尺度转而描述对象新的特征, 结果随尺度的变化不符合原分维数的推算, 发生质变。因此若描述具有变维分形特征的对象, 并非尺度越精细越准确, 因为尺度超过对应特征区间的左侧边界时对该特征的描述必然失真。综上, 特征区间左边界是描述对应特征最精确的尺度, 而右边界则是能有效描述该特征的最粗略尺度。

图6 不同尺度下的沙滩形态特征
3.2 单界定参数的取值
海岛数量界定目的在于筛选出利用价值高、海洋权益大且数量稳定的海岛, 以提高海岛资源管理的能效, 而界定方法是否合理的关键在于如何确定界定参数的取值。界定值过大, 纳入管理体系的海岛数量偏少, 将造成海岛资源的浪费; 界定值过小, 纳入管理体系的低价值海岛偏多, 又会影响海岛的有效管理。
一般来说, 海岛的面积越大, 越易于开发利用; 间距越远, 给予的海洋权益越大。依据基岩海岛的地质成因, 将本文的海岛分为构造类和海蚀类两类。构造运动时间尺度和空间尺度都较大, 故所形成的海岛在短时期内是稳定的, 且面积大、岛间距远, 利用价值也高。反观海蚀作用形成的海岛, 依附于海岸浅滩存在, 海岛新增和灭失现象频发, 故所形成海岛数量不稳定, 且面积小、岛间距短, 利用价值较低。因此合理的海岛数量界定方法应将构造类海岛纳入海岛管理而排出海蚀类。依本文计算结果, 海岛面积和海岛间距两方面的分维数都在较大尺度端稳定, 其特征区间的左边界分别为ln=2.69和ln=3.35, 即=220 m2、=28.5 m。由于构造类海岛刚好对应着大面积远间距的特征, 故可假设分维数稳定的区间为构造类的特征区间。也就是说,>220 m2的海岛属于构造类;>28.5 m的海岛属于构造类。使用小于上述界定值的尺度描述海岛, 将渐脱离构造类特征进入海蚀类特征, 致使海岛数量冗多, 对海岛管理的资源造成浪费。因此, 在界定嵊泗县海岛的数量时, 单独使用海岛面积合理界定值应为220 m2, 单独使用海岛间距合理界定值应为28.5 m。
3.3 多界定参数的取值
在实际的海岛数量界定中, 往往利用多种界定参数组合判断, 而非单一的参数。海岛面积因其直观且与利用价值关联紧密常作为优先指标。例如, “浙江908专项”先将满足面积大于500 m2的较大海岛纳入数量统计, 而后再利用50 m间距对剩余海岛进行筛选补充。那么优先界定参数的取值大小对其他辅助界定参数取值的影响如何呢?本文同样以海岛面积为主海岛间距为辅, 以200、300、400和500 m2为面积界值, 分4种情况筛选出面积大于面积界值的海岛作为大岛, 并以余下小岛与大岛的间距为界定参数, 计算小海岛的分维数序列, 结果如图7所示。结果表明余下的小海岛数量与海岛间距同样存在着变维分形特征, 且小海岛的分维数显著小于全体海岛。随面积界值的增大, 同间距尺度下的分维数降低, 其中200~300 m2的降幅较大, 300、400和500 m2之间的降幅较小。分维数稳定的区间方面, 余下海岛数量的特征区间较之全体海岛向右偏移, 且上述4种情况下, 均偏移至ln=3.9(=50 m)附近。结合上文的讨论, 经过200~500 m2的面积筛选后, 海岛间距大于50 m的海岛归属构造类分形特征。在嵊泗县海岛范围内, 使用200~500 m2的面积作为优先界定参数时, 余下海岛间距的合理界定值应为50 m, 该值恰巧与“浙江908”中的界定值相同。
综上, 在分形理论下, 所得最佳界定方法为优先对面积大于220 m2的海岛计数, 再将海岛间距大于50 m的余下海岛补充计数, 所得嵊泗县海岛界定数量为681个。

图7 面积筛选后海岛数量与海岛间距的分维数
4 结论
本文通过高分辨率遥感影像提取嵊泗县海岛地理信息, 使用分形理论的研究方法, 以海岛面积和海岛间距为界定参数, 探讨海岛界定数量与界定参数取值之间的联系。随后, 利用变维分形的思想, 讨论合理的界定值大小, 得到了以下结论。(1)2008年嵊泗县可影像识别的海岛数量为2 875个, 其中面积大于4 m2的海岛2 113个, 海岛间距大于2 m的海岛2 586个。(2)绝大多数的海岛都分布在小面积、短间距的区间之中, 超过50%的海岛面积不超过50 m2, 间距不足6 m, 且随着面积或间距的增大, 海岛分布密度持续降低。(3)海岛界定数量在海岛面积和海岛间距两方面都存在分维数先增加后稳定的变维分形特征, 在海岛面积大于220 m2, 海岛间距大于28.5m时, 海岛界定数量的分维数趋于稳定。(4)变维分形特征显示嵊泗县海岛合理的界定方法为先对面积大于220 m2的海岛计数, 再将余下海岛中间距大于50 m的海岛补充计数, 所得数量为681个。
致谢:
本文的完成得益于贾建军、时连强、刘毅飞、蔡廷禄、王宁、曹一峰等参与“浙江908专项”海岛调查同志们的辛苦工作, 华东师范大学贾建军教授对文章的修改提供了帮助。在此一并致谢。
[1] 宋小棣. 浙江海岛资源综合调查与研究[M]. 杭州: 浙江科学技术出版社, 1995. Song Xiaodi. Survey and Research of The Island Resource in Zhejiang[M]. Hangzhou: Zhejiang Science and Technology Presss, 1995.
[2] 夏小明, 贾建军, 陈勇, 等. 中国海岛(礁)名录[M]. 北京: 海洋出版社, 2012. Xia Xiaoming, Jia Jianjun, Chen Yong, et al. China Islands Directories[M]. Beijing: China Ocean Press, 2012.
[3] Mandelbrot B B. How long is the coast of Britain?[J]. Science, 1967, 156: 636-638.
[4] 国家海洋局908专项办公室. 我国近海海洋综合调查与评价专项海岸线修测技术规程[M]. 试行本. 北京: 海洋出版社, 2007. State Oceanic Administration, People’s Republic of China, 908 Project Office .Chinese Offshore Investigation and Assessment Project Coastline Measurement Technical Regulation[M]. Beijing: China Ocean Press, 2007.
[5] 孙伟富, 马毅, 张杰, 等. 不同类型海岸线遥感解译标志建立和提取方法研究[J]. 测绘通报, 2011, 3: 41- 44. Sun Weifu, Ma Yi, Zhang Jie, et al. Study of remote sensing interpretation keys and extraction technique of different types of shoreline[J]. Bulletin of Surveying and Mapping, 2011, 3: 41-44.
[6] 李静, 张鹰. 基于遥感测量的海岸线变化与分析[J]. 河海大学学报(自然科学版), 2012, 40(2): 224-228. Li Jing, Zhang Ying. Analysis of coastline change based on remote sensing measurement[J]. Journal of Hohai University (Natural Sciences), 2012, 40(2): 224-228.
[7] 国家海洋局908专项办公室. 海岛界定技术规程[M]. 北京: 海洋出版社, 2011. State Oceanic Administration, People’s Republic of China, 908 Project Office. Specifications for Island Definition Techniques[M]. Beijing: China Ocean Press, 2011.
[8] 汪富泉, 李后强. 分形——大自然的艺术构造[M]. 济南: 山东教育出版社, 1996: 7-36. Wang Fuquan, Li Houqiang. Fractal: the Art Structure of Nature[M]. Ji’nan: Shangdong Education Press, 1996: 7-36.
[9] 苏媛媛, 李钦帮, 侯敏. 黄河三角洲海岸线分形研究[J].资源与产业, 2008, 10(6): 103-107. Su Yuanyuan, Li Qinbang, Hou Ming. Stydy on coastal fractal of Yellow River delta[J]. Reaources & Industries, 2008, 10(6): 103-107.
[10] 王欣凯, 贾建军. 浙江海岛岸线分维数与其人工岸线比例的关系[J]. 海洋学研究, 2011 , 29(4): 25-37. Wang Xinkai, Jia Jianjun. Relationship between the fractal dimension and percentage of artificial coastlines of islands in Zhejiang Province[J]. Journal of Marine Sciences, 2011, 29(4): 25-37.
(本文编辑: 刘珊珊)
The variable fractal dimensions characterizing of the statistical number of islands — a case study of Shengsi County
WANG Xin-kai1, 2, XIA Xiao-ming2, CHENG Lin3
(1. School of Earth Sciences, Zhejiang University, Hangzhou 310012, China; 2. The Second Institution of Oceanography, State Oceanic Administration, Hangzhou 310012, China; 3. Institute Geographical Sciences, Hebei Academy of Sciences, Shijiazhuang 050051, China)
It is imperative that the oceanic authority who manages the islands count them. However, because of the inconsistencies in statistical standards, different numbers of the islands in China can be attained. This paper examines the islands of Shengsi County as a case study and uses the fractal theory to determine the most suitable standard by which to count islands. From high resolution remote-sensing images, 2 875 islands were detected visually in Shengsi County; more than half of these are smaller than 50 m2in area or with a separation distance shorter than 6 m. In both aspects of island area and separation distance, the relevant statistics for island numbers display the characteristics of variable fractal dimensions. At first the fractal dimensions increase then stabilize at 1.80 and 2.25 for areas larger than 220 m2and distances greater than 28.5 m, respectively. For islands separated by 200, 300, 400 and 500 m2, the number of smaller islands and their separation distances from the larger islands also display the characteristics of variable fractal dimensions. And for separation distances greater than 50 m, the fractal dimensions are stable for each of the four cases previously discussed. Therefore, the rational standard for counting islands in Shengsi is by screening out those islands larger than 220 m2and then by supplementing them with those islands whose separation distance is larger than 50 m. Using this method, the number of islands in Shengsi is 681.
number of islands; area of islands; distance of islands; variable fractal dimension
Dec. 23, 2016
王欣凯(1986-), 男, 湖北武汉人, 博士在读, 主要从事海岸带、海岛调查与管理研究, 电话: 0571-81963500, E-mail: carlinwxk@163.com
P714
A
1000-3096(2017)09-0130-06
10.11759/hykx20161223001
2016-12-23;
2017-03-19
国家自然科学基金(41576095); 我国近海海洋综合调查与评价专项(908-ZC- I-09, ZJ908-01-02)
[National Science Foundation of China, No. 41576095; Chinese Offshore Investigation and Assessment Program, No. 908-ZC-I-09, No. ZJ908-01-02]

