不确定数据聚类综述
罗来源+孙国宝
摘要:近年来,在无线射频识别、地球信息系统等领域中大量出现了不确定数据。不确定数据的研究早在上世纪八十年代就已经开始,但早期的不确定数据的研究方向主要集中在不确定数据管理、不确定数据查询等。不确定数据的聚类分析,正成为研究热点。目前,不確定数据聚类研究主要通过对经典聚类算法进行扩展。该文首先对不确定数据进行了概述,以及对基于划分的不确定聚类算法进行了介绍,最后对未来发展趋势进行了探讨以及总结。
关键词:不确定数据;聚类;扩展;概述;基于划分
中图分类号:TP393 文献标识码:A 文章编号:1009-3044(2017)01-0215-03
1 引言
近年来,随着技术的进步和人们对数据采集和处理技术深入地研究,不确定数据(uncertain data)得到广泛的重视。在许多现实的应用中,例如:经济、军事、物流、金融、电信等领域,数据的不确定性普遍存在,不确定数据扮演关键角色1[1]。传统的数据管理技术却无法有效管理不确定数据,这就引发了学术界和工业界对新型的不确定数据管理技术的兴趣。不确定数据,即带有不确定性(uncertainty)的数据。不确定性是针对确定性而言的,是对确定性的否定。在经典科学的理解上,把确定性(certainty)理解为一个现象或事件结果的出现是唯一的、确定的。因此,不确定性则是对这种唯一性的否定,即当某一事件即使遵循某一规律运动也不能最终出现唯一的结果2[2]。例如,多次投掷一枚骰子,骰子有六面分别有六个不同的点数,每一次投掷的结果都是六个点数其中的一个,但具体是哪一个点数无法确定,那么就可以称每一次投掷的结果就是不确定的。
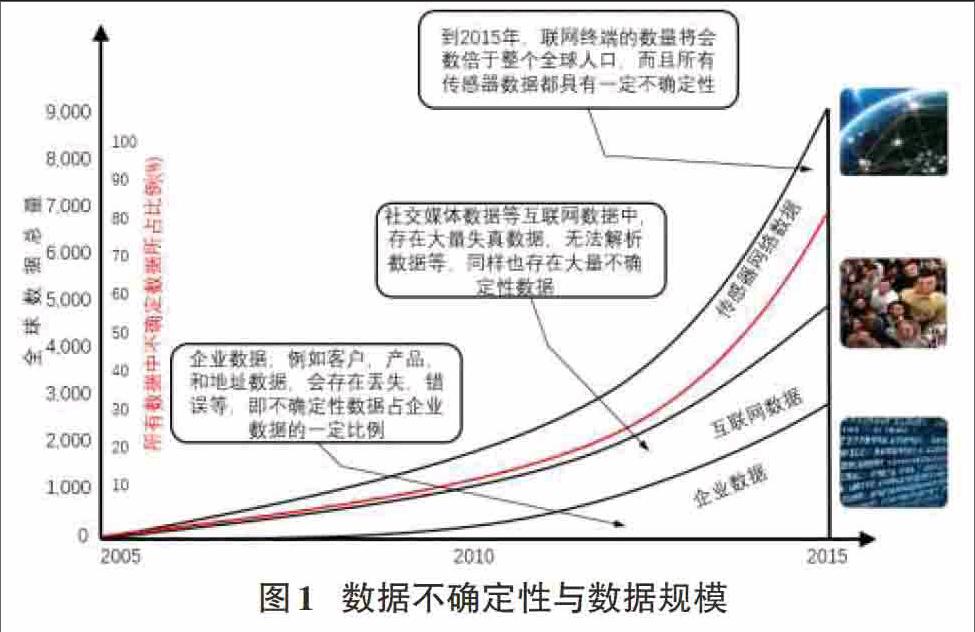
不确定数据的研究从上世纪八十年代末就已经开始了,其中主要的研究方向包括:不确定数据的表示与模型3[3-6]、不确定数据查询4[7-10]等。目前,不确定数据正呈爆炸式增长,如图1所示描述了随着数据规模的增加,不确定数据所占的比例也相应地增加,其中红线表示在数据中不确定数据所占的比例。截止到2015年,世界上80%的数据是不确定的[11]。对于大量不确定数据进行数据挖掘得到可利用的知识是当前研究的热点,聚类分析研究是不确定数据挖掘的重要组成部分。聚类就是将多个数据对象构成的集合分成若干相似对象的子集合的过程。不确定数据聚类算法的研究最早在2005年被提出,由M.Chau和郑振刚等人5[12]提出并对不确定数据挖掘进行了定义。
2 不确定数据聚类
2.1 不确定数据概述
数据不确定性产生的原因复杂,李雪等人6[13]将不确定数据产生的原因分为两类,一类是被动的不确定性,另一类是主动的不确定性。被动不确定性主要由原始数据因为自身缺失、不精确等;主动不确定性数据产生的原因则是人为对原始数据进行处理,例如对数据进行扰动以达到数据隐私保护的目的而形成的数据。
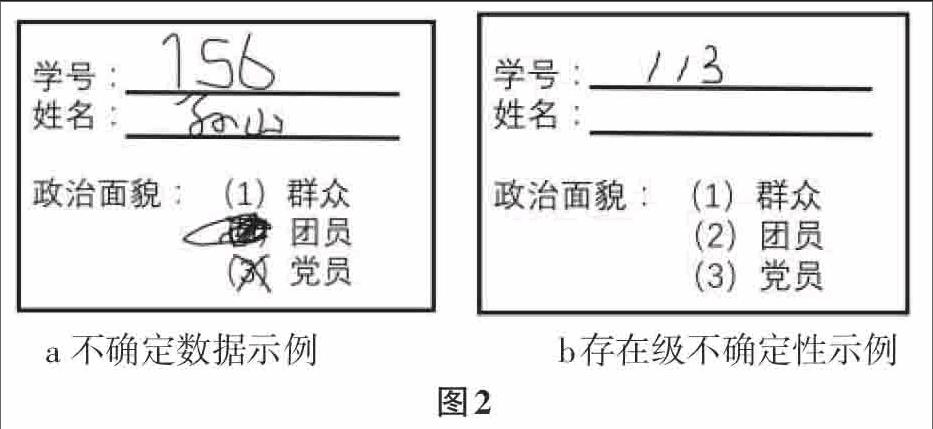
如图2a为一张某研究所新生注册中,新生孙山的入学信息调查表,由于该同学字迹潦草等原因致使学号一栏可能是756,也有可能是156,仅从图2a无法得出真实的学号数据。在政治面貌一栏中由于污渍涂写错误等原因致使政治面貌一栏结果也无法获得。本次调查孙山的面貌数据和学号数据看作为不确定数据,并且这两项不确定性被称为属性不确定。
图2b所示,该研究所收到的另外一张学号为113的调查表,政治面貌缺失,姓名一栏为缺失,我们将无法确定学号为113的该名学生是没有完成这个表格还是因为某种原因该生并没有到校注册,那么可以将学号为113的学生的调查数据称为不确定数据,而且为存在级不确定。即按表现形式数据不确定性可以分为存在级不确定性和属性级不确定性。存在级不确定性指某实例是否存在是不确定的,属性级不确定性指实例属性值是不确定的7[14]。
不确定数据聚类的研究是继不确定数据模型与表示、不确定数据管理和不确定数据查询后又一个不确定数据研究领域的热点。
2.2 不确定数据聚类
聚类(cluster)被视作为无监督学习,在模式识别和机器学习等领域具有广泛的应用背景8[15]。聚类的目标是把有限的无标签的对象集划分为多个“相似的”簇(clustering)集,而“相似性”体现了数据本质的类别属性。在引文[12]中,作者引入了带坐标移动散布点的例子,很好地引出了不确定数据聚类的概念。
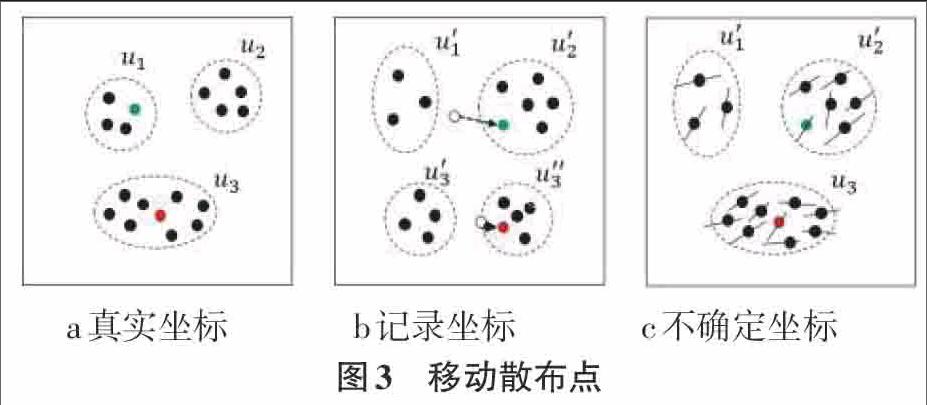
如图3所示,图中散布点表示的移动对象,散布点的坐标表示对象当前的坐标。图3a为根据真实坐标聚类成3个簇 。图3b为在时间间隔之前的记录坐标,同样根据对象坐标进行聚类对当前坐标进行预测,然而得到的结果是四个簇,与图3a真实坐标聚类明显不同。其原因在于,聚类过程中,并未将对象坐标的改变考虑其中。假设在对图3b记录坐标数据进行聚类时,将每个对象移动的趋势考虑进去,用概率密度函数pdf (probability density function)表示每个对象的坐标,再进行聚类得到的结果如图3c所示,和图3a真实的聚类结果非常接近。
通过数学表达式对不确定数据对象及聚类进行定义如下:
定义1:给定n维向量空间:
(1) 点以概率出现在事件中,则称为维空间一个不确定点或不确定实例。称 为不确定实例二元组。
(2) 对于不确定二元组和,则称和为同点二元组,记为;反之则称和为异点二元组,记为。
定义2:对n维向量空间中,任意不确定实例的集合满足,不确定实例出现概率之和为1,即:
则可称集合为n维向量空间中的不确定对象。
如图4所示,在某2维向量空间中, 表示的是一组由6个不确定实例组成不确定实例二元组的集合,且 。集合,即可称为2维空间的一个不确定对象。
与确定数据相似,不确定数据对象的聚类过程也是将相似的对象划分到对应簇中,把相异的对象划到不同簇内,表1给出了不确定数据对象聚类的形式化描述:
同样,我们也可以用散布图对不确定数据聚类进行描述如图5所示,散布点表示不确定对象所对应的不确定实例,实线表示的为不确定对象,图5中共有5个数据对象,对这5个数据对象进行聚类分析,得到2个簇和,和为对应簇心,如图虚线所示。
不难发现,当每个不确定数据对象都只有一个实例的情况下,不确定数据聚类就退化成为传统确定数据的聚类。不确定数据聚类相较传统确定数据聚类的不同在于对聚类对象新增了不确定因素,而不确定因素正是由不确定对象的多个实例造成的。目前不确定数据聚类研究的成果主要为基于划分的不确定数据聚类以及改进算法。
3基于划分的不确定聚类算法
不确定数据聚类研究的主要路线,是对传统聚类算法针对不确定数据的扩展,其中基于划分的不确定拒类是重要研究成果。基于划分的不确定聚类算法包括Chau等人提出的UK-means算法和Gullo等人9[16]提出的UK-medoids算法。
3.1 UK-means算法
UK-means 算法与K-means 算法的过程大致相同,算法假定不确定对象,相应不确定实例区域由概率密度函数 表示。不确定对象到簇心的距离,由对象所对应不确定实例到簇心的距离的期望表示。将各个数据对象划分到离它最近的簇,然后重新计算簇心,进行迭代直至算法收敛。UK-means 算法步骤如表2所示:
UK-means算法与K-means算法的不同在于:不确定数据对象与簇心的距离是由对象所对应实例到簇心的距离期望表示,而且其中误差平方和准则函数为:
表示的是实例到簇心的欧氏距离。
算法每次迭代,不确定对象与簇心的期望距离都要被计算一次,对于个不确定数据对象聚类成k个簇,UK-means算法要在每次迭代中需要计算次距离期望,正是由距离期望的计算导致UK-means算法效率很低。算法的使用场景也受到限制,例如,算法使用确定的单个数据点作为簇中心,这在不确定数据中聚类中容易丢失数据的不确定信息,从而影响了聚类质量。针对这个问题,Gullo等人提出了UK-medoids算法。
3. 2 UK-medoids算法
基于K-medoids算法扩展的另一个基于划分的不确定聚类算法UK-medoids,选择真实的不确定对象做为簇中心进行聚类。由于簇中心是在实际输入的数据对象之中选择,只需对各个数据对象之间的距离做一次计算。UK-medoids算法步骤如表3所示。
UK-medoids算法优点在于,减少了距离期望的计算次数。引文[13]实验证明,对于同一数据集,UK-medoids算法的聚类精度和效率要比UK-means算法高。
4 不确定聚类所面临的挑战
与传统的面向确定性数据的聚类分析相比,不确定性数据聚类主要在以下两个方面面临着挑战。首先面临着聚类算法的时间复杂度过高的挑战,也是目前不确定数据聚类实际应用时,所面临的最直接的挑战,对象数量的增加导致不确定实例数量呈指数倍的增加。算法的时间复杂度过高严重影响算法的实用性。面对这个问题,当前所提出的解决方法主要是采用多种剪枝策略,压缩不确定实例的规模从而降低算法的计算当量,但往往会失去一部分不确定实例,降低聚类质量。
不确定数据对象维度的增加,同样是不确定聚类所面临的巨大挑战。高维不确定聚类需要解决的不仅在于算法复杂度方面的增加,更在于建立数据模型来表示不确定对象、相似性度量函数以及有效的降维,维度之咒不仅是聚类所面临的挑战同样也是其他计算机学科所面临的挑战。
5总结
本文首先对不确定数据进行了概述,形式化描述了不确定数据对象、不确定聚类。并详细地介绍了基于划分的不确定数据聚类算法。文末对不确定聚类所面临的挑战进行了阐述。
参考文献:
[1] 周傲英.不确定性数据管理技术研究综述[J]. 计算机学报, 2009, 01:1-16.
[2] 李坚.不确定性问题初探[D]. 中国社会科学院研究生院, 2006.
[3] Aggarwal C C. Managing and Mining Uncertain Data[M]. Springer Publishing Company, Incorporated, 2009.
[4] Sarma A D. Working Models for Uncertain Data. [C]. ICDE. IEEE Computer Society, 2010:7-7.
[5] Aggarwal C C. Models for Incomplete and Probabilistic Information[M]. Current Trends in Database Technology – EDBT 2006. Springer Berlin Heidelberg, 2010:278-296.
[6] Sadri F. Modeling uncertainty in databases[C]. International Conference on Data Engineering, 1991. Proceedings. 1991:122-131.
[7] Sen P. Representing and Querying Correlated Tuples in Probabilistic Databases[C]. IEEE International Conference on Data
Engineering. 2007:596-605.
[8] Dalvi N. Efficient Query evaluation on Probabilistic Databases[C]. Thirtieth International Conference on Very Large Data Bases. 2004:864-875.
[9] Dalvi N. Answering Queries from Statistics and Probabilistic Views. [C]. International Conference on Very Large Data Bases, Trondheim, Norway, August 30 - September. 2005:805-816.
[10] Burdick D. OLAP over uncertain and imprecise data[J]. Vldb Journal International Journal on Very Large Data Bases, 2007,16(1):123-144.
[11] 陈静玉. 面向不确定数据流的聚类和模式挖掘技术研究[D]. 西安电子科技大学, 2014.
[12] Michael Chau. Uncertain Data Mining: An Example in Clustering Location Data[C]. Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Springer-Verlag, 2006:199-204.
[13] 李雪, 不確定数据挖掘技术研究进展[J], 2009.
[14] Aggarwal C C. A Survey of Uncertain Data Algorithms and Applications[J]. IEEE Transactions on Knowledge & Data Engineering, 2009, 21(5):609-623.
[15] 数据挖掘:概念与技术[M], 机械工业出版社, 2007.
[16] F. Gullo, G. Ponti, and A. Tagarelli. Clustering uncertain data via K-medoids[C]. In Proc. SUM Conf., pages 229–242, 2008.

