杨氏双缝干涉实验的影响因素研究

苏婉娥

（福建师范大学 闽南科技学院，福建 泉州 362332）

杨氏双缝干涉实验的影响因素研究

苏婉娥

（福建师范大学 闽南科技学院，福建 泉州 362332）

杨氏双缝干涉实验是光学理论的重要组成部分，为了能够简便的运算，大部分教材皆对实验做了理想化处理，认为光源和狭缝的宽度为0，在这个假设下，干涉条纹一定是等间隔均匀分布的而且整个视场中条纹可见度恒为1.双缝距屏的距离、光源距双缝距离还有实验装置中光源及双缝的宽度均为有限宽度，这些因素都会造成实验结果的差异.本文针对缝宽、间距、光源等因素对杨氏双缝干涉实验的影响进行了分析探讨.

杨氏双缝干涉；缝宽；间距；光源；条纹分布

杨氏双缝实验利用精巧的设计让单个波正面分解为两个波正面，为了探究光的干涉现象用锁定两个光源间相位差的方法，使光的干涉现象顺利的被实验展现出来，在历史上首次测定了光的波长，为光的波动学说的建立奠定了基础，并且用波动理论做了很好的说明，初步测定了光波波长，从而验证和支持了惠更斯等人的光的波动理论，它第一次用实验方法证明了光的波动性.

杨氏实验是把两个点光源作为光的干涉实验的典型代表，以简便的实验仪器和精巧的想法就实现普通光源来做干涉，它不只是大部分其他光学的干涉设备的原型，在原理上还能够从中得到很多重要的概念和启发，不管从经典光学还是从现代光学的角度分析，杨氏实验都具有非常重要的意义.

1 杨氏双缝干涉实验装置

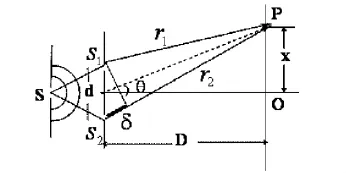
图1 杨氏双缝干涉实验原理图

杨氏实验的仪器在普通单色光源前放一个开有小缝S的屏幕，作为单色点光源.在单色点光源能够照明的区域内前方，再放一个开有两个小缝的S1和S2的屏.S1和S2到S的距离相等并且它们之间距离较近.依照惠更斯原理，S1与S2将作为两个向前发射次波，形成交迭的波场.这两个相干的光波在距离屏为D的接收屏上叠加，形成干涉图样.为了提高干涉条纹的亮度，实际中S，S1和S2用三个互相平行的狭缝（杨氏双缝干涉），而且可以不用接收屏，而代之目镜直接观测，这样还可以测量数据用以计算[1].在激光出现以后，利用它的相干性和高亮度，人们可以用氦氖激光束直接照明双孔，在屏幕同样可获得一套相当明显的干涉条纹，供许多人同时观看.

如图1杨氏双缝干涉实验原理图假定S1和S2到S的距离相等，S1和S2处的光振动就是具有相同的相位，屏幕上各点的干涉强度将由光程差ΔL决定.为了确定屏幕上光强极大和光强极小的位置，选取直角坐标系o-xyz，坐标系的原点O位于S1和S2连线的中心，x轴的方向为S1和S2连线方向，假定屏幕上任意点P的坐标为（x,y,D），那么S1和S2到P点的距离r1和r2分别写为:

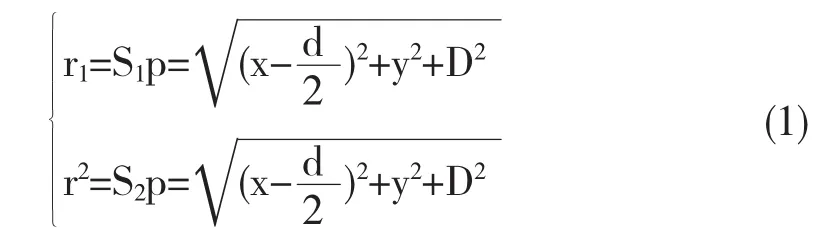
由上两式可以得到r22-r12=2xd

若整个装置放在空气中，则相干光到达P点的光程差为:

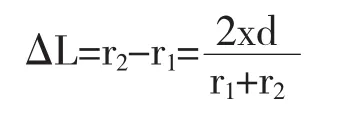
在实际情况中，d＜D，这时如果x和y也比D小的多（即在z轴附近观察）则有r1+r2≈2D.在次近似条件下上式变为:

再由光程差判据

mλ0(m=0,±1,±2，…)p为光强极大处.

可知道在屏幕上各级干涉的极大的位置为:

干涉极小的位置是:

相邻两极大或两极小值之间的间距为干涉条纹间距，用Δx来表示，它反映了条纹的疏密程度.由(3)式的相干条纹的间距为

式中:d——两个狭缝中心的间距

λ——单色光波波长

D——双缝屏到观测屏（微测目镜焦平面）的距离

这就是本实验所要使用的原理公式.从实验中测得D，d以及x，即可由上式算出λ.

2 通过实验分析影响杨氏双缝干涉实验的因素

2.1 缝宽的大小

在“杨氏实验”中，s是一个很小的狭缝（或小孔），通过s的光照射到s1和s2上，在光屏上形成明暗相间的干涉条纹.同学们往往提出，这个狭缝s的存在是否有必要？若用一个普通光源代替s，光屏上不可能出现干涉条纹.因为干涉条件要求，只有同一波列自身之间才能发生干涉，不同的光源之间，以及同一光源的不同部分发出的光都不能满足想干条件.由于狭缝s的存在，且s很小.光波到达s1、s2就成为发射柱面波（s若为小孔，则发射球面波）的波源.它们又各发出一个柱面（或球面）形次波.由于这两个次波来自同一个波面，因此它们的频率相同；由于s1与s2距离很近，因此振动方向近似一致；又由于s1和s2的振动位相差保持一定.所以这两列光波满足相干条件，这是利用分波阵面法获得相干光波的典型方法.在实验中，缝的大小将影响实验的结果，当缝的大小s大于某一值时，将不能观察到光的干涉现象.当缝的大小s小于某一值时，将出现衍射现象，也不能观察到干涉现象.

图2、图3、图4分别是双缝宽度为0.16mm的双缝在单缝缝宽为30mm、90mm、120mm时的干涉图样，通过实验图片对比，可以清晰的看出单缝为30mm的时候光强较弱，出现的明暗条纹中间部分比较清晰；在90mm单缝缝宽的时候光强较强，明暗相间的条纹看的也比较清楚；在120mm缝宽的时候光强也较大，出现的明暗条纹也较多，但是已经出现衍射的现象了，也就是说超过了缝宽的范围后就会开始出现衍射现象，因此，在做实验的时候这个缝宽要控制好，不然要是出现衍射现象就会影响到做杨氏双缝干涉实验的实验数据.

图2 单缝缝宽为30m

图3 单缝缝宽为90mm

图4 单缝缝宽为120mm

2.2 双缝到屏间距的大小

但是经过多次实验发现，当波长λ与双缝间距d不变时，增大双缝与屏幕间距D，条纹间距△x反而变小，后来经过反复实验发现，当D小于16.5cm时，保持波长λ与双缝间距d不变，增大双缝与屏幕间距D，条纹间距△x反而变小；当D达到16.5cm时，图像的明暗条纹消失；当D大于16.5cm时，图像慢慢出现明暗条纹，保持波长λ与双缝间距d不变，D增大，△x也跟着增大.因此，在做杨氏双缝干涉实验时应注意双缝到屏的距离要大于16.5cm.

以下为实验结果图:

图5 D为10cm

图6 D为16.5cm

图7 D为22cm

图5至图7是杨氏双缝干涉实验从D为10cm到D为22cm的实验过程图[2]，由图可以直观的看出当D从10cm增加到16.5cm时，图像的明暗条纹逐渐变小直到消失；当D从16.5cm增加到22cm时，图像的明暗条纹从消失到逐渐变大.

2.3 不同光源对杨氏双缝干涉的影响

任何两个独立的普通光源都不是相干光源，光的辐射起源于物质的原子或分子.在两个通常独立的光源中，或甚至在同一发光体的不同部分，一般说来原子的辐射可认为是互不相关的（激光光源除外）.在一批发出辐射的原子里，由于能量的损失或由于周围原子作用，辐射过程常常中断，延续时间很短（约10s）.接下来，另外的原子发光，却已经拥有另一个初相位，所以不同原子所发出的辐射之间的相位差，将再每一次新的辐射开始时发生改变，也就是说，每经过一个极短的时间间隔，相位差就会改变，所以这样的光源所发出的光是不相干的.

在实验中，使用的是钠光灯和激光光源进行实验的对比，比起钠光灯，由于激光光源具有光线较集中，光强较高和方向性好的特点，观察的明暗条纹也会更明显一些，比较有利于直观的看到实验结果，但是杂光会比钠光灯多；钠光灯虽然杂光较少，但是由于光线较暗，要在相对黑暗的条件下才能观察的到，并且光线较暗，观察者往往要调节好看测微目镜的视角才能观察的到明暗相间的条纹，极易造成眼睛的视觉疲劳，并且实验中用测微目镜读取数据时成像效果差，容易造成实验误差.

以下是实验结果图:

图8 激光光源实验结果图

图9 钠光灯实验结果图

由图8和图9对比可知，图8图像清晰，可见度高；相反的，图9成像效果较差，较模糊，容易造成实验误差.因此，通过实验对比激光光源较钠光灯更适用于杨氏双缝实验.

3 提高杨氏双缝干涉实验效果的方法探讨

正常来说，进行杨氏双缝干涉实验所用的光源基本为钠光灯，用测微目镜看实验现象.虽然实验的原理相对简单，但是实验的时候对实验的环境要求比较严格，要求环境要相对黑暗，并且在实验中用测微目镜观察到的图像很不理想，光线较差，又要找对角度才能观察得到实验的数据图像，经常要花费较多的时间去测量数据，因此极易造成人眼的疲累.测微目镜里面的成像屏的位置不确定，也会使实验的数据有偏差[3].由于这些影响因素，建议应把进行实验所用的光源由钠光灯改为激光光源，并注意实验仪器的摆放位置，缝宽的大小和双缝到屏的距离这些因素都要注意，以减少实验误差.

4 结语

杨氏双缝干涉实验是光学领域内的主要组成部分，它的实验装置虽然比较简单，但直接影响实验结果的因素也不少，本文总结了3个比较主要的影响因素:缝宽的大小、双缝到屏的间距的大小和不同光源.在做实验的时候这个缝宽的大小范围要控制在小于等于λ，要是超过了λ就会出现衍射现象从而影响到实验的实验结果；实验的同时还要注意双缝到屏的距离要大于16.5cm，因为当距离小于16.5cm的时候，实验的结果与理论是相反的，即当波长λ与双缝间距d不变时，增大双缝与屏幕间距D，条纹间距△x反而变小.因此，在做杨氏双缝干涉实验时应注意双缝到屏的距离要大于16.5cm.不同的光源也会对实验的结果产生影响，比起钠光灯，由于激光光源具有光线较集中，光强较高和方向性好的特点，观察的明暗条纹也会更明显一些，比较有利于直观的看到实验结果，从而能够减少实验中产生的实验误差.这些在实验中都要引起注意.

〔1〕赵占娟,阎冰,张红江.干涉实验装置对干涉图样影响的教学讨论[J].河北职工医学院学报，2004 (04)：53-56.

〔2〕陈泽婵,陈靖,严雷,张运超.基于Unity3D的移动增强现实光学实验平台 [J].计算机应用,2015 (S2)：199-204.

〔3〕彭小兰,王红成,刘敏霞.杨氏双缝干涉实验的改进[J].广东技术师范学院学报，2012（06）：11-14.

O436.1

A

1673-260X（2017）02-0006-03

2016-09-20

2016年福建师范大学闽南科技学院高等教育教学改革研究项目（FJSF2016052）