基于NESSUS的杜瓦结构可靠性分析

王春生，张 磊，东海杰



基于NESSUS的杜瓦结构可靠性分析

王春生，张 磊，东海杰

（华北光电技术研究所，北京 100015）

为了提高杜瓦结构的可靠性水平，本文提出了基于NESSUS（Numerical Evaluation of Stochastic Structures Under Stress）软件的杜瓦结构可靠性分析方法。此方法将杜瓦组件的载荷、材料性能、几何尺寸等参数均作为具有某种分布特性的随机变量，通过概率分析，可获得定量的杜瓦结构可靠度值以及各个设计参数的概率灵敏度值，并由此确定关键影响因素，为提高杜瓦结构的可靠性提供设计依据。本文以杜瓦冷台支撑结构为例进行了结构可靠性分析，分析结果表明此方法可以显著提高杜瓦结构的可靠性水平。

结构可靠性；NESSUS；可靠性仿真分析；杜瓦结构

0 引言

杜瓦为红外焦平面探测器提供良好的低温工作环境以及光、机、电、热传输通道，是红外焦平面探测器的封装和保护装置，也是红外焦平面探测器完成工程化、实用化的重要环节[1]。因此，杜瓦结构的可靠性对整个红外焦平面探测器组件的可靠性有着重要的影响。杜瓦中包含十几个关键零部件，其材料特性及所承受的载荷都存在一定的离散性。例如，在测量材料的物理参数时必须将实际材料制成一定规格的试件，施加特定载荷并记录变形情况，从而计算出物理参数。但是，通过多次实验获得的物理参数值并不是一个唯一值，而是具备某种分布特性的一组值，表现出一定的分散性。这种分散性将导致设计结果的不确定性，带来一定的风险。

目前杜瓦结构的设计与分析采用的是确定性方法。该方法隐含了下列假设：①对于设计参数可以实现完备的测量；②设计参数与结构响应间存在确定性关系；③在给定设计方案下，其制造、安装和运行中各种因素可以实现完全控制。显然在实际工程中，这种假设是很难实现的。因此，确定性方法的设计结果存在风险。为此，在确定性设计中引入一定的安全系数来降低不确定性风险。但安全系数法只是一种简单的经验方法，无法准确定量地评价可靠程度，也不能识别影响组件可靠性的关键参数或关键失效模式，不利于风险控制和优化设计[2-3]。同时，它也无法从理论上解释按安全系数法设计为安全的系统，在使用中却发生失效的现象。另外，安全系数法通常采用最坏情况假设，会带来较大的冗余设计，造成结构体积、重量增加，不适合机载、星载、弹载等特殊应用场合的需求。因此现行的基于安全系数法的确定性设计很难满足红外焦平面探测器杜瓦结构的可靠性保障要求。随着红外探测应用领域的不断拓展，对红外探测器组件可靠性的要求日益提高，需要开展系统化的杜瓦结构可靠性设计和仿真分析工作。

近年来国内外相关机构针对红外探测器杜瓦结构进行了可靠性评价与加速寿命实验等方面的研究，文献[4]中介绍法国SOFRADIR公司的杜瓦真空寿命已达到20年，文献[5]分析了SOFRADIR公司的杜瓦在振动、机械冲击以及温度冲击下的失效模式。国内近年来通过加速寿命实验对杜瓦真空寿命进行了研究，文献[6-8]均采用阿列尼乌斯模型对红外杜瓦的真空寿命进行了研究。但是迄今为止，在设计和仿真分析领域，杜瓦结构设计仍然采用的是确定性方法，无法满足工程实际的需求。本文结合杜瓦结构的特点和可靠性要求，提出了基于结构可靠性仿真软件NESSUS（Numerical Evaluation of Stochastic Structures Under Stress）的杜瓦结构可靠性仿真分析方法，并以冷台面支撑结构为例进行了可靠度计算和设计参数灵敏度分析，分析结果对杜瓦结构的可靠性设计具有重要的指导意义。

1 基于NESSUS的结构可靠性仿真分析方法

1.1 结构可靠性定量分析

工程实际中，杜瓦结构的强度和应力都是呈某种分布的随机变量，因此，以广义应力-强度干涉模型作为可靠性仿真分析的理论基础。图1表示出了应力-强度干涉模型的具体形式，将应力和强度的分布曲线画在同一坐标系中，横坐标代表应力和强度的数值，纵坐标代表二者的概率密度。

图1中应力和强度相互交叠的区域即为可能发生失效的区域，在此区域内强度可能小于应力。结构的可靠度就是强度大于应力的概率，由式(1)所示：

＝(＜)＝[(－)＞0] (1)

式中：为结构可靠度；为广义应力；为广义强度。

理论上，结构可靠度可由公式(2)计算得出：

但在工程实际中式(2)是很难求得解析解的。结构可靠性分析就是通过对影响可靠性的各种性能指标进行概率计算，得到定量的可靠性值，并以此为依据对结构设计进行改进，满足可靠性要求。同时，在量化分析的基础上得到较小的零件尺寸、体积和重量，从而在研发过程中平衡设计保守和设计不足的矛盾，解决安全系数不能综合量化可靠性的问题。

1.2 灵敏度分析

在概率分析中，灵敏度表示概率随分布参数（如均值和方差）的改变而变化的程度，由下式定义：

＝¶/¶(3)

式中：为结构的失效概率；为随机变量的分布参数。

灵敏度分析可定量地给出影响结构可靠性的主要因素，可用于指导结构设计改进和结构故障预测[9]。若某参数对可靠性影响较大，则应采取相应的优化设计和工艺控制手段，降低其不确定性。反之，若某参数对结构可靠性的影响不显著，则可在下一步的可靠性改进设计中将其作为确定量值处理，以减少随机变量的数目，提高计算效率。

1.3 基于NESSUS的可靠性仿真分析

NESSUS是美国西南研究院的结构可靠性分析软件，它本身具有非常丰富的概率算法，并且通过调用有限元分析软件来共同完成结构的可靠性计算。该软件可定量评估零件、系统的可靠度，识别重要随机变量，为结构可靠性设计提供依据，并由此开发出比传统确定性设计方法更经济、更有效、更可靠的产品。基于NESSUS的结构可靠性仿真分析流程如图2所示[10]，分析是自上而下逐步进行的，首先进行问题描述和随机变量定义，然后是模型定义、分析类型选择、执行分析，最后显示分析结果。

从可靠性的角度分析，红外探测器组件杜瓦结构的可靠性工程具有如下特点：

1）受力条件复杂

杜瓦结构件除受到静载荷、振动载荷外，还受到极大的热应力作用，载荷的复杂性使得可靠性仿真分析中的极限状态方程无法求得解析解，必须借助有限元模型进行数值求解。而概率分析中需对有限元模型中的相关参数进行扰动处理，并多次进行计算。该过程极为复杂，并且计算量极大，必须采用专业的概率分析软件进行。

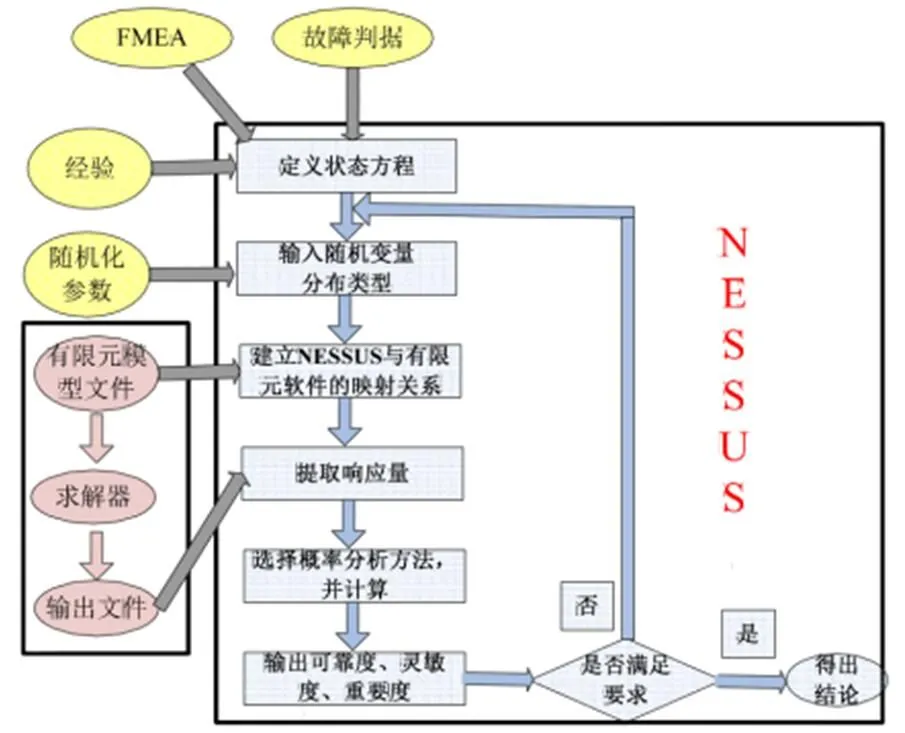
图2 基于NESSUS的结构可靠性仿真分析流程

2）存在关键结构件

杜瓦内存在多个关键的结构件，各关键结构件都有其自身的工作特点和可靠性指标，对关键件进行定量的可靠性仿真分析是提高杜瓦整体可靠性水平的重要手段。同时，通过灵敏度分析可以明确对可靠性影响最大的关键参数，找出最有效的改进方法。例如，冷台面支撑结构作为红外探测器的承载平台，是杜瓦结构的关键件，需对其进行定量的可靠性分析。该支撑结构为薄壁、细长的悬臂结构，其材料特性、外载荷以及零件尺寸的变化均影响其可靠性，可以通过灵敏度分析找出影响最大的参数，并加以改进。

以下，本文将以杜瓦的冷台面支撑结构为例，详细论述基于NESSUS的杜瓦结构可靠性仿真分析方法。

2 建立有限元模型

如前所述，杜瓦结构的极限状态方程难以求得解析解，必须借助有限元模型进行数值求解。有限元模型在可靠性仿真分析中所处的地位如图3所示。

本文采用ANSYS软件进行有限元建模与求解。NESSUS通过ANSYS的参数化功能对ANSYS的模型参数进行随机参数映射，然后，由NESSUS修改指定输入文件中相应的概率统计值，并递交给ANSYS进行求解。最后，NESSUS通过解析指定的输出文件，得到响应值。

冷台面支撑结构的有限元分析模型如图3所示，约束条件为施加在法兰端面的固定约束，载荷为随机振动载荷，模型的关键参数为支撑柱的内径、外径、长度以及材料的弹性模量和泊松比。

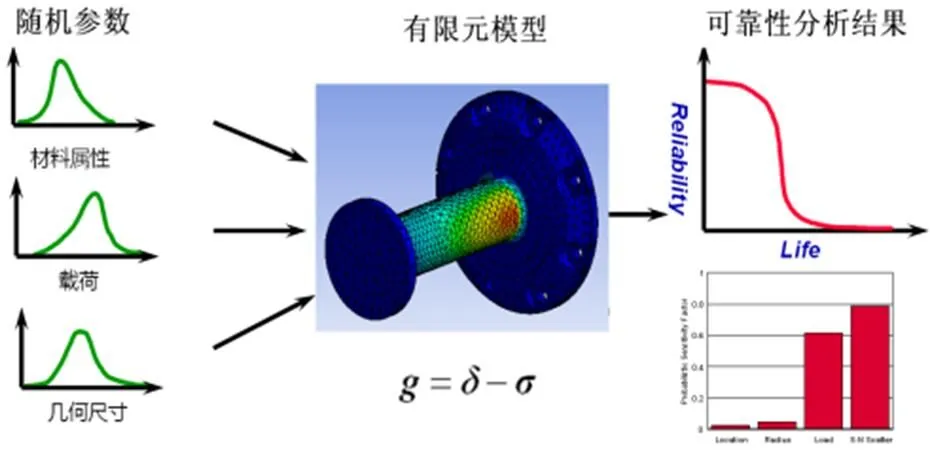
图3 结构可靠性分析解决方案示意图

3 建立可靠性仿真分析模型

可靠性仿真分析是进行可靠性改进设计的先决条件，只有通过重要度、灵敏度分析后才能确定改进的方向，并采取针对性的改进措施，例如优化设计参数、加强工艺过程控制、提高加工一致性等，进而实现可靠性的提升。要对杜瓦结构进行可靠性分析，首先要明确其功能、主要载荷以及与之相对应的主要故障模式，并且要找到影响结构性能与故障的主要设计参数。

3.1 极限状态函数定义

极限状态指的是应力与强度相等时的临界状态，当超过此状态时结构就会发生失效。以数学公式表达为极限状态函数：

＝－(3)

式中：为极限状态函数；为广义应力；为广义强度。

在本例中，冷台面支持结构承受随机振动载荷的作用，并产生变形，由此引起探测器芯片相对于光轴发生位置变化。当探测器的位置变化达到一定程度时将影响成像质量，尤其是当系统对MTF（Modulation Transfer Function，调制传递函数）要求比较高时，过大的位置变化将成为一个主要的失效模式。因此，本例中以探测器芯片位置变化小于7mm为极限状态函数，如式(4)所示：

＝0.007－＝disp(i,o,x, Pr) (4)

式中：为极限状态函数；为探测器芯片位置变化量；i为支撑柱内径；o为支撑柱外径；为支撑柱长度；x为弹性模量；Pr为泊松比。

3.2 随机变量定义

进行可靠性仿真分析首先要确定设计变量及其分布类型。本文将冷台面支撑结构的材料特性（包括弹性模量x、泊松比Pr）以及几何尺寸（包括内径i、外径o、长度）均作为随机变量，其分布类型及参数如表1所示。

3.3 仿真分析结果

在NESSUS软件中选择选择概率分析方法为AMV＋方法，分析计算后得到概率累积分布函数和参数灵敏度分别如图4、图5所示。

由分析结果可见，在随机振动作用下，冷台面支撑结构位移失效的可靠度为82%（置信度为95%），可见该结构在该工况下无法满足可靠性要求，需对设计方案加以改进。

概率灵敏度分析表明弹性模量x是影响冷台面支撑结构可靠性的主要因素。因此，选用更高规格的材料，并严格控制材料的采购、标识和使用环节，降低材料特性的离散程度。同时，由灵敏度分析可见，几何参数的不确定性对可靠度的影响较小，在进一步的分析中可将其视为确定性量，以简化概率分析模型。

3.4 设计改进

如表2所示，忽略几何参数的影响，将材料弹性模量x的标准差缩小，重新进行概率分析。

重新计算的累积分布结果如图6所示。

由分析结果可见，仅改进一个设计参数（弹性模量x的标准差），便可将可靠度提升到99%，由此可充分体现出基于NESSUS的可靠性仿真分析方法的优势。

4 结论

本文结合红外探测器杜瓦结构的特点和可靠性要求，提出了基于NESSUS的杜瓦结构可靠性仿真分析方法，并以冷台面支撑结构为例进行了可靠性仿真分析。该方法将载荷、材料性能、几何尺寸等设计参数均视为具有某种概率分布的统计量，应用概率统计方法与强度理论求出零部件的可靠度，从而更加真实地反映可靠性水平，有效解决了传统确定性设计不能量化可靠度的问题。采用该方法还可以通过重要度、灵敏度分析识别影响可靠度的主要因素和主要失效模式，进而有针对性地加以改进，有效提高杜瓦结构的固有可靠性水平。

表1 原设计随机变量表

图4 累积分布函数

图5 随机变量灵敏度

表2 改进设计随机变量表

图6 改进后的累积分布函数

[1] 王小坤, 朱三根, 龚海梅. 长线列碲镉汞红外焦平面微型杜瓦的研究[J]. 激光与红外, 2006, 36(11): 1047-1050.

WANG Xiaokun, ZHU Sangen, GONG Haimei. The study of the micro dewar for long linear HgCdTe IRFPA[J]., 2006, 36(11): 1047-1050.

[2] Moon Byung, Kang Gyung J U, Kang Beom Soo. Dynamic and reliability analysis of stochastic structure system using probabilistic finite element method[J]., 2004, 18(1): 125-135.

[3] 陈孝添. 在型号设计中应用结构可靠性设计方法[J]. 强度与环境, 2003, 30(2): 43-48.

CHEN Xiaotian. Applying the design of structural reliability to structure engineering[J]., 2003, 30(2): 43-48.

[4] Brenière X, Tribolet P. IR detectors design and approach for tactical applications with high reliability without maintenance[C]//, 2008,6940: 69400H-1-69400H-13.

[5] Molina M, Brenière X, Tribolet P. IR detector dewar and assemblies for stringent environmental conditions[C]//, 2007, 6542: 65422N-1- 65422N-11.

[6] 黄燕, 吴全信. 阿列尼乌斯模型在红外微型金属杜瓦的真空寿命实验研究中的应用[J]. 低温与超导, 2005, 33(2): 69-72.

HUANG Yan, WU Quanxin. The application of arrhenius model in the experimental study on the vacuum life of infrared miniature metal dewar[J]., 2005, 33(2): 69-72.

[7] 林日东, 刘伟, 王冠, 等. 红外焦平面探测器杜瓦组件真空寿命分析[J]. 激光与红外, 2011, 41(7): 779-783.

LIN Ridong, LIU Wei, WANG Guan, et al. Vacuum life analyses of infrared detector ＆ dewar assembly[J]., 2011, 41(7): 779-783.

[8] 张亚妮, 朱三根, 龚海梅. 微型杜瓦组件真空加速寿命实验的研究[J].红外, 2008, 29(3): 11-15.

ZHANG Yani, ZHU Sangen, GONG Haimei. Research on vacuum life of micro metal dewar[J]., 2008, 29(3): 11-15.

[9] 周红, 刘永寿, 高宗战, 等. 某型导弹舱段连接结构强度可靠性灵敏度分析[J]. 固体火箭技术, 2011, 34(6): 768-771.

ZHOU Hong, LIU Yongshou, GAO Zongzhan, et al. Analysis on strength reliability and parameter sensitivity of a missile cabin structure[J]., 2011, 34(6): 768-771.

[10] 周新建, 万正平, 周长国. 基于NESSUS的汽车前桥可靠性灵敏度分析[J]. 机械设计, 2009, 26(1): 66-68.

ZHOU Xinjian, WAN Zhengping, ZHOU Changguo. Sensitivity analysis on reliability of automobile front axle based on NESSUS[J]., 2009, 26(1): 66-68.

NESSUS-Based Reliability Analysis for Dewar Structure

WANG Chunsheng，ZHANG Lei，DONG Haijie

(,100015,)

To improve the reliability level of a dewar structure, in this paper, a NESSUS(numerical evaluation of stochastic structures under stress)based reliability analysis method for a dewar structure has been proposed. In this method, the design parameters, such as the loads, material characters, and geometry parameters, are treated as random variables with specified distributions. Through probabilistic analysis, this method can obtain the quantitative reliability index of the dewar structure and the sensitivity factors of every design parameter can be calculated. According to the analysis results, the key parameters of dewar structure reliability can be recognized which can be used to improve the dewar design. As an example, the reliability of a cold platform was analyzed in this paper. The results indicate that this method would dramatically improve the reliability of a dewar structure.

structure reliability，NESSUS，reliability simulation，dewar structure

TN215

A

1001-8891(2017)10-0903-05

2016-09-20；

2016-10-20.

王春生（1974-），男，黑龙江延寿人，华北光电技术研究所高级工程师，博士，研究方向为红外探测器杜瓦结构设计、有限元分析及可靠性分析。E-mail：w_chunsheng2003@163.com。