深水气井井筒压力温度分布数学模型的建立
周楠楠
深水气井井筒压力温度分布数学模型的建立
周楠楠
(中国石油集团长城钻探工程有限公司钻井技术服务公司,辽宁 盘锦 124000)
针对在进行凝析气井生产动态分析以及优化设计过程中深水凝析气井井筒压力、温度分布预测、采气工艺等重要问题。考虑应用SRK状态方程与相平衡闪蒸计算模型结合的方法并对此方法进行充分研究。想要构建以相态变化的深水凝析气井的井筒压力和温度耦合的计算模型为基础的计算模型。然而深水凝析气井还存在井身温度分布不规律,气井在海水中暴露的长度较大,井身的传热与地层部位有不同的规律。凝析气还存在井筒里面发生的相态变化比较复杂,这些问题导致单单是设计计算模型是不远远够的。最终还要利用四阶龙格库塔法对计算模型进行解答才能预得到较为完整的数学模型。这样便可以利用建好的数学模型并且通过提供实际的数学参数计算得出水凝析气井井筒内压力以及温度分布。该模型能够预测出水中气井的生产动态分布等问题,能为今后的深水采气工作提供完整数学理论基础。
深水凝析气井;温度分布;压力分布;总传热系数
深水凝析气开发时,一般会出现当着井筒压力降低时,井筒内的凝析气会发生凝析从而形成凝析油的现象[1],导致井筒内出现油气两相同时运移的情况,严重影响开采成果。从微观角度来看,压力减小时,因为分子之间的相互引力减小[2-3],从而使得重烃分子受到轻烃分子的引力减小后重烃分子便从气体混合物中脱离出来从而重烃分子聚集在井底形成凝析油[4]。
虽然凝析气藏中的重烃组分具有较高的经济效益,但是在生产过程中很难幵采。因为在凝析气开采过程中因速度不断降低,轻烃质的含量逐渐增多所以就不具备足够的能量将凝析油携带出井口[5-6]。这些问题均是目前油气藏开采所需要解决的难点和重点。现如今国内外关于凝析气井温度、压力分布的研究绝大多时候是以陆地的油田特点为对象而进行研究的,对于考虑深水凝析气井的温度和压力计算的方法的相关文献还很少。O'Dell和Miller (1967)[7],提出了一种采气率的计算方法他们利用拟压力函数来描述井筒周围凝析液对气井的产能有影响。考虑海上气井与陆地气井有很大差异,海上气井中有比较长的井段位于海水中,而海水的传热过程和陆地地层热传过程有很大的差异。因此建立伴随气/液相态发生变化的深水凝析气井筒内部的温度、压力分布的数学模型对日后的深水凝析气井生产动态的分析与优化设计应用与研究具有重要意义[8-9]。
1 混合物体性质的计算
由于SRK状态方程在预测纯烃及混合烃的气-液平衡时的准确度较高,因此选用SRK状态方程来计算初始混合物的压缩因子及密度。


式中:
其中:—油管截面积。


m—气相混合物和液相混合物的分子量。


2 传热模型的建立
在地层部位,地层和井身套管之间由水泥环相互隔开。稳定传热非稳定传热分别发生在套管和水泥环中间,水泥环和地层中间,忽略存在油,套俩管间的导热热阻和因油管内壁的对流形成的换热热阻,在地层段的总传热系数简化如下方程:
热系数简化如下方程:

在海水与空气隔开段之间,如果没有水泥环,热交换就会改为套管与海水或套管与空气的对流换热热阻[10]。海水空气段总传热系数如下:

3 综合模型的建立
计算时就要简化运算,对于凝析气井筒温度、压力[11],一般作如下假设:
① 气体流动状态为稳定单向流动;
② 假设井筒内传热为稳定传热;
③ 假设地层传热为不稳定传热;
④ 油套管同心。
气体在从井底通向井口,此过程满足质量、动量以及能量三种守恒定律。在这过程中,气体也遵循状态方程[12]。井筒内部的流体流动常常没有不变的热源,能量来自井筒内的流体对地层或海水进行热传递。在这个过程当中,如果流体向地层或海水散热,流体就会依次经过油管、油套环形空间、套管以及水泥环,这就有质量与流量发生变化,这是导致温度场发生一定的变化的主要原因[13-14];但当质量流量趋于平稳,温度场也随之趋于平稳。
流体要从井底通向到井口,而在这个过程中流体的能量会有损耗,而损耗分一般分为俩部分,一部分能量是向地层或海水散热而损耗,另外一部分是因摩阻损失而损耗[15-16]。考虑到海上油井基本不存在直井,故还应考虑井的倾斜角度。综上,管流压降示意图如下:

图1 管流压降示意图
守恒方程的建立如下:

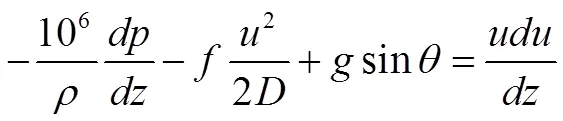

—流速,m/s。
通过物体径向传热公式,做出如下讨论:

稳定流动可以认为只有一个流动阶段,q可以进一步表示为:

式中:—单位长度井筒在单位时间内的热损失,W/m。
温度与压力之间的关系函数被称为气体的比焓,油管内气体流动的过程中,管径基本不变,所以焦耳一汤普逊系数是小到可被忽略的[17]。所以可令:
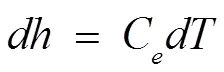
式中:——定压比容。
将公式(7)、公式(8)代入式(5),简化为:

或

式中:—井筒内流体温度,K;
T—地层初始温度,K;
—质量流量(=),kg/s。
式中:

式中:—重力加速度常数,9.81 m/s;
—摩阻系数;
—地层导热率,J/M/K。
气体压力、温度、流速和密度4个量在质量、动量和能量守恒这几个方程中是4个未知数,方程发散不好求解。如想要方程收敛从而使方程能够求解,此时则需补充方程如下:

式中:M—凝析气的分子量;
—通用气体常数,0.008 314 3 MPa·(kg-mol·K)。
将前面提出的方程组进行整理,就可得到模型完整的方程组,如下:

式中:—压力,MPa。

—油管内径,m;
—地面温度,K;
由井底气体的压力和温度,根据状态方程求出混合物的初始密度及初始速度,并以此作为方程的边界,最后用四阶龙格库塔法求解方程组。
4 结 论
(1)建立深水凝析气井的温度与压力分布计算模型,不仅可以应用四阶龙格库塔法对模型进行求解,而且模型还增加了相态变化与位于海水中井身部位的传热规律。
(2)由于海水的传热系数大于地层的传热系数,所以在海水段的井筒温度梯度大于位于地层中的井筒段的温度梯度。
(3)利用该模型计算的结果与实际情况的数据相比误差较小,满足工程精度需要。
[1] 廖新维. 气藏/凝析气藏不稳定流动理论研究[D]: 北京中国石油勘探开发研究院,2003: 30-31.
[2] 何志雄,杜竞,孙雷,王雷,林涛. 低气液比凝析气井井筒动态预[J]. 天然气勘探与开发,2009:29-31.
[3] 秦积舜,李爱芬. 油层物理学[M]. 东营: 石油大学出版社,1998: 65-67.
[4] 郭天民. 多元汽液平衡与精馏[M]. 北京:石油工业出版社,2002: 173-180.
[5] 李士伦. 天然气工程[J]. 北京:石油工业出版社,2000: 117-127.
[6] 金玉宝,卢祥国,刘进祥,等. 疏水缔合聚合物传输运移能力及其作用机理[J]. 石油化工,2017, 46(5):600-607.
[7] 马铭勖,辛一男. 凝析气藏反常凝析现象的解释[J]. 内蒙古石油化工,2011:4-5.
[8] 李志芬. 凝析气井生产系统优化设计[D]. 青岛中国石油大学(华东),2003:6-7.
[9] 刘通,李颖川,钟海全. 深水油气井温度压力计算[J]. 新疆石油地质,2010:181-183.
[10] 李颍川. 采油工程[M]. 北京:石油工业出版社,2009:35-37.
[11] 赵福麟,张贵才,周洪涛,等.二次采油和三次采油的结合技术及其进展[J].石油学报,2001,22(05):38-42.
[12] 刘伟伟. 凝析气井生产系统参数优化设计方法研究[D]. 青岛中国石油大学(华东),2009:17-18.
[13] 李忠兴,韩洪宝,程林松,等.特低渗油藏启动压力梯度新的求解方法及应用[J].石油勘探与开发,2004,31(3):107-109.
[14] 曾一非. 海洋工程环境[M]. 上海:上海交通大学出版社,2007:42-43.
[15] 毛伟,梁政. 气井井筒压力、温度耦合分析[J]. 天然气工业,1999, 19(6):66-69.
[16] 曾祥林,刘永辉,李玉军. 预测井筒压力及温度分布的机理模型[J].西安石油学院学报,2003, 18(2): 40-44.
[17] 杨桦. 凝析油气体系基础物性参数的计算分析[J]. 钻采工艺,1996, 19(4):34-40, 19(5):28-37.
Establishment of Mathematical Model for Wellbore Pressure and Temperature Distribution in Deepwater Gas Wells
(PetroChina Great Wall Drilling Company Oil Drilling Technology Services Branch, Liaoning Panjin 124000, China)
In order to solve the important problems in the condensate gas well production dynamic analysis and the optimization design process, the wellbore pressure and temperature distribution prediction and gas production technology in deep condensate gas wells were analyzed. The method of combining SRK state equation with phase equilibrium calculation model was used, and the method was analyzed and researched. A computational model based on the computational model of wellbore pressure and temperature coupling in a deep water condensate gas reservoir with phase change need be established. However, there are still some problems in the deep condensate gas wells, such as irregular temperature distribution, big exposed length of the gas well in the sea, and different heat transfer of the well from that of the formation. The phase change of condensate gas in wellbore is complicated, which leads to the fact that the design calculation model is not enough. Finally by using four-order Runge-Kutta method to solve the calculating model, a more complete mathematical model can be obtained. Thus, it is possible to calculate the wellbore pressure and temperature distribution of the condensate gas well by established mathematical model and providing the actual mathematical parameters. The model can be used to predict the production dynamic distribution of gas wells in water, which can provide a complete theoretical basis for the deep water gas production in the future.
deep water condensate well;temperature distribution;pressure distribution;overall heat transfer coefficient
TQ 018
A
1004-0935(2017)09-0905-04
2017-06-23
周楠楠(1985-),男,工程师,山东省威海人,2009年毕业于西南石油大学石油工程专业,主要从事钻井及完井技术研究。E-mail: znnbit@126.com。

