基于全光谱拟合法的VO2薄膜光学常数计算

侯典心，路 远，宋福印



基于全光谱拟合法的VO2薄膜光学常数计算

侯典心1,2,3，路 远1,2,3，宋福印1,2,3

（1. 电子工程学院，安徽 合肥 230037；2. 红外与低温等离子体安徽省重点实验室，安徽 合肥 230037；3. 脉冲功率激光技术国家重点实验室，安徽 合肥 230037）

为实现对VO2薄膜光学常数的测量，本文在全光谱拟合法的基础上，首先利用导纳矩阵法推导出透射率与薄膜厚度、折射率以及消光系数的函数关系，然后利用单纯形法得到其优化函数。最后采用Matlab编程方法对低温态、高温态VO2薄膜的红外透射率进行了全光谱拟合，得到折射率和消光系数等VO2薄膜光学常数的拟合曲线。结果表明：拟合曲线与已有研究结果及实测曲线基本吻合。采用全光谱拟合方法得到的光学常数能较准确的对VO2薄膜进行描述，为最佳膜厚设计提供了依据。此外，为更简便地描述VO2薄膜的光学常数，本文还引入了Cauchy色散模型方程，对全光谱拟合方法得到的中远红外波段（2.5～15mm）的光学常数结果进行了拟合。

薄膜光学；VO2薄膜；全光谱拟合；单纯形法；Cauchy色散模型

0 引言

随着光电技术的快速发展，大量具有不同特殊性质薄膜的应用日趋广泛。在高质量投影、屏幕显示、精密光学等技术领域，针对薄膜设计的研究也不断深入。薄膜设计中，为保证薄膜的性能发挥到最佳水平，设计方案需要依赖准确的薄膜光学常数测试数据[1-2]。VO2薄膜作为一种金属-绝缘体相变材料，是近年来研究的热点之一[3-4]。随着VO2薄膜制备方法及设备呈多样化发展，所制备的VO2薄膜折射率、消光系数等光学常数也不尽相同。因此需要针对不同情况，对在不同条件下制备的VO2薄膜进行单独分析计算[5-6]。

目前，薄膜光学常数的测试方法包括非光学测量与光学测量两大类。非光学测量方法包括a粒子法、超声波法等，主要适用于对光学特性依赖程度不高的薄膜。随着精密光学仪器技术的发展成熟，使得目前薄膜光学常数的测试通常采用光学测量方法[7]，主要包括椭圆偏振法[8]、棱镜耦合法[9]、光谱反演法[10]三种。

其中椭圆偏振法具有极高的灵敏度和精度，厚度与折射率测量精度分别可达0.1nm和10－4，然而其测量需要昂贵的设备和复杂的计算模型，同时其测量范围太小，无法实现对VO2薄膜的中红外（3000～6000nm）与远红外（6000～15000nm）光学常数的测试。棱镜耦合法具有实验仪器简单、操作方便、精度较高等优点，但其需要膜层厚度大于300～480nm，一般情况下制备的VO2薄膜厚度可能达不到其测量要求，因此同样不适合用于VO2薄膜的光学常数测量。光谱反演法是利用分光光度计、光谱仪等仪器测得薄膜光谱透射率或光谱反射率，然后根据薄膜光学常数与光学特性的关系，并结合与薄膜材料特性相关的光学模型、物理模型等，反演推导得到折射率以及消光系数等光学常数的方法。光谱反演法具有测量范围大，测量设备简单，测试精度高等优点，十分适合用于VO2薄膜的光学常数测量。目前常用的光谱反演法包括包络线法[11]、K-K法[12]、全光谱拟合法[13]等。包络线法依赖于入射光在膜层内经过多次反射与折射形成的多光束干涉振荡，需要膜层厚度足够大且吸收特性较弱，故该方法不适用于膜层厚度较小且具有吸收特性的VO2薄膜。K-K法仅依靠光谱反射率()就能直接计算得到薄膜的光学常数，但是目前的分光光度计和光谱仪等仪器很难测量薄膜的绝对反射率，同时反射率的测量精度较低，因此K-K法的使用也受限。

当薄膜的测试条件不满足以上测试方法的要求时，全光谱拟合法就体现出其优势。由于目前对VO2薄膜红外光谱透射率测量的精度较高且操作方便，该方法可仅依靠薄膜的透射率曲线，通过采用非线性回归模型并建立目标优化函数，结合计算机编程拟合的方法反演计算得到折射率、消光系数。因此本文采用全光谱拟合法对VO2薄膜的光学常数进行计算。

1 全光谱拟合法拟合原理

1.1 Si基底VO2薄膜的透射率函数

薄膜反射率或透射率的计算一般采用导纳递推法、菲涅耳系数递推法或导纳矩阵法等，本节采用目前使用较广泛的导纳矩阵法推导Si基底VO2薄膜的透射率。

根据多层膜系的光学特性，薄膜的吸收特性与光路方向均不影响膜系的透射率，因此假设薄膜中电磁场分布如图1所示。根据电磁场的边界条件，可知入射光与出射光的电矢量与磁矢量之间的关系：

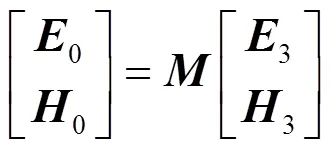
Fig.1 Distribution of the electromagnetic field of the thin film

界面两侧连续，则：

0＝(0×0) (3)

2＝2(0×2) (4)

因此式(8)可简化表示为：

式中：为膜系的有效位相厚度：

令：

则式(8)表示为：

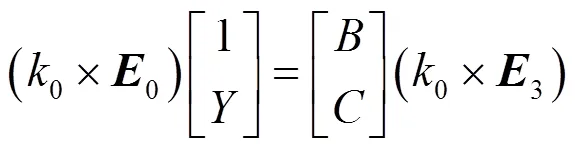
所以

＝/(9)

式中：为膜层和基底的组合导纳，得到该膜系的透射率为：

式中：0、2分别为空气和基片的的有效光学导纳。

雅特乐器是昌乐为数不多坚持主打自主品牌的乐器厂之一。为了推广自主品牌，雅特乐器厂与山东艺术学院、四川音乐学院等国内多所高校建立校企合作关系，为这些学校教学提供乐器支持，同时，他们为推广吉他弹奏艺术，还与一些中小学共同成立了吉他课堂，并连续赞助举办了多届鄌郚音乐节和全国电吉他大赛。

根据有效光学导纳的定义：

在光波段≈1，光学导纳等于折射率，则：

相变前的VO2薄膜呈半导体性质，因此薄膜可能具有一定的色散特性，因此定义VO2薄膜复折射率为1为：

1＝－i(13)

式中：为折射率；为消光系数。则其有效位相厚度为：

由以上推导，可唯一确定薄膜厚度、折射率以及消光系数与透射率的函数关系：

＝(,,) (15)

1.2 基于单纯形法的函数优化

采用单纯形法对薄膜光学常数的计算过程进行优化。由于该方法受初始结构的影响较小，同时不需要计算导数，因此非常适合多个变量且表达式复杂的计算情况，在光学薄膜参数优化中具有广泛的应用[14]。定义目标优化函数：

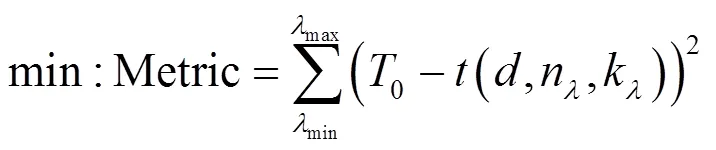
式中：min、max为计算光谱范围内波长最小值与最大值，0为波长对应的实际透射率。由该式可知，目标优化函数中包含有3个相互独立的变量（、、），而计算机对3个独立变量同时拟合会大大增加计算负荷。为简化计算过程，可以根据前期的测试结果，在目标优化函数中预先设定薄膜厚度＝350nm，则优化函数变为：

在由＋1个自变量初始值构成的维空间中，单纯形法在优化过程中会在该维空间中进行反射、延伸等多种变换，充分压缩单纯形直至使优化目标函数得到极小值，此时所对应的自变量取值即为优化参数。对于一般的光学薄膜，折射率取值范围一般为1.3～7，考虑到VO2薄膜相变前后透射率出现急剧变化，而消光系数变化范围同样较大，因此定义二者的取值范围都为0～10。

2 拟合结果与误差分析

2.1 拟合结果

采用Matlab编程方法对低温态、高温态VO2薄膜的红外透射率进行全光谱拟合，得到薄膜2.5～25mm光学常数拟合结果，分别如图2、图3所示。

目前对VO2薄膜在2.5～25mm近红外波段光学常数的研究较多，然而由于VO2薄膜制备方法多样，各方法制备薄膜的光学常数变化规律无法完全保持一致。宋婷婷[15]等通过电子结构与复介电函数的关系，得到溅射法制备的VO2薄膜3～5mm复折射率。该薄膜单斜态折射率（2.1～3.5mm）及消光系数（0.5～1.4mm）与金红石态折射率（3.8～4.1mm）及消光系数（2.9～3.3mm）与本文计算结果符合较好。但与Xiao D等[16]得到的金红石态折射率（1.4～1.7mm）存在误差，而消光系数（3.5～4.2mm）又符合较好，其原因可能与不同价态钒的组分含量等多种因素有关。通过与已有研究结果的比较，表明单纯形拟合法得到的消光系数及折射率等光学常数具有一定的准确性。

根据拟合得到的光学常数，可重新计算得到薄膜2.5～25mm波段的光谱透射率，其拟合结果与实测透射率曲线的对比结果，如图4所示。

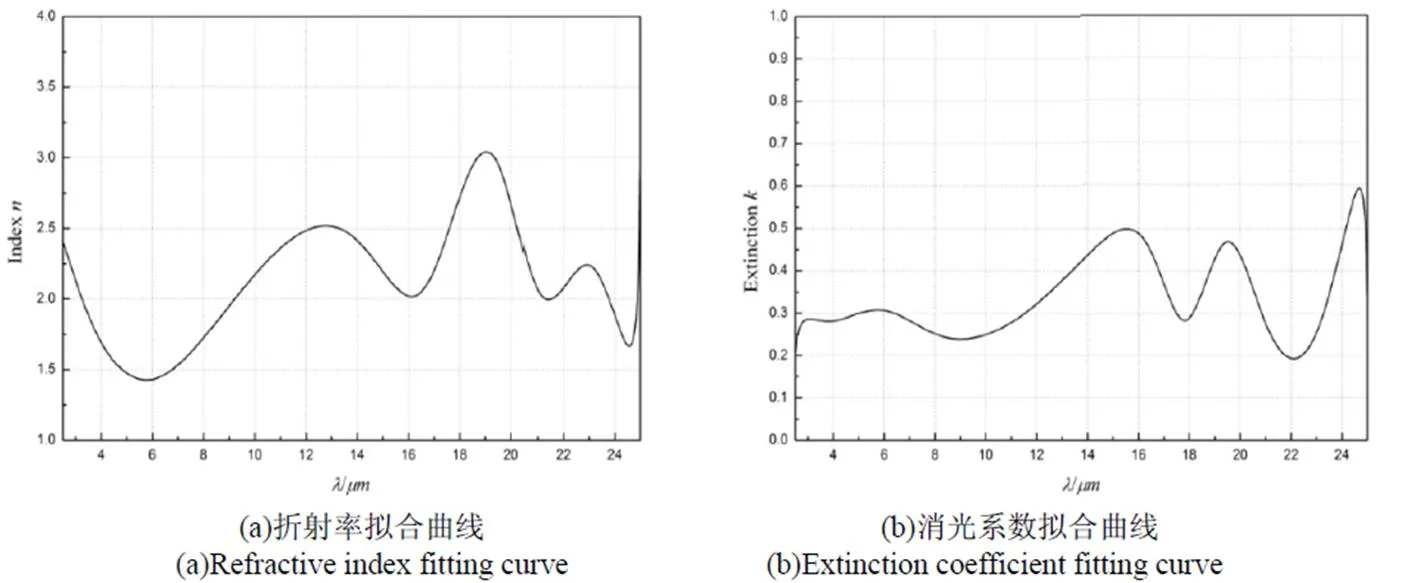
图2 低温态光学常数拟合结果

Fig.2 Fitting results of optical constants in low temperature state

图3 高温态光学常数拟合结果

Fig.3 Fitting results of optical constants in high temperature state

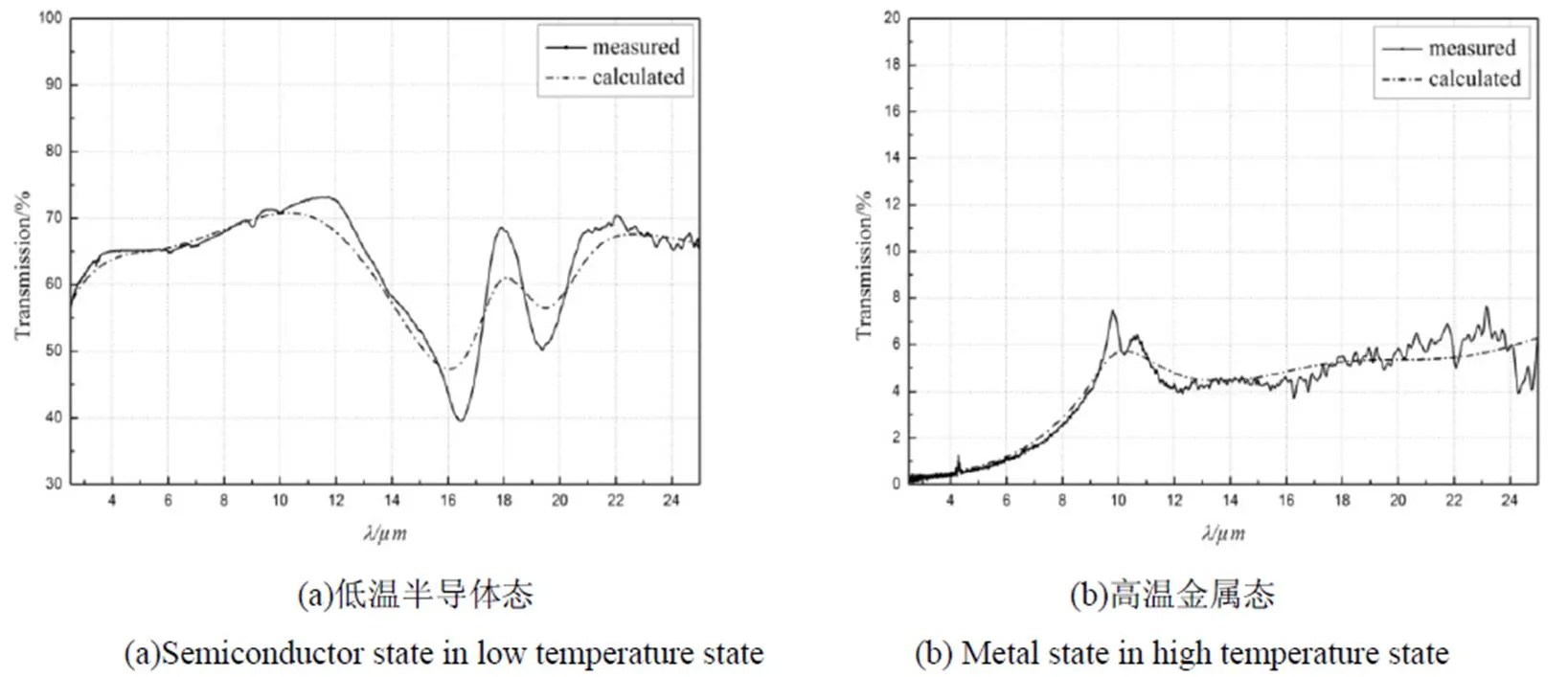
图4 拟合与实测透射率对比

2.2 误差分析

由图4(a)可以看出，低温半导体态的拟合透射率曲线在12.5～22.5mm与实测透射率曲线出现偏离，而在其他波长范围内吻合较好。由图4(b)可以看出，高温态拟合透射率曲线在整个0～24mm波段与实测透射率曲线基本吻合，但在10～11mm，20～23mm出现微小偏离，因而出现误差。原因是全光谱拟合算法是根据实测结果，采取不断采样计算、比对结果并重新采样计算的过程。而重新采样的点是从以原采样点为中心的一定范围内选取的，因此该计算无法对透射率出现较大波动的波段进行精确拟合，但从整体角度上来看拟合结果与实测结果比较吻合。这表明全光谱拟合法也可以较好地描述实际透射率的变化规律。

3 Cauchy色散模型拟合

为更简便地描述VO2薄膜的光学常数，本文引入光学色散模型方程，对全光谱拟合方法得到中远红外波段（2.5～15mm）的光学常数结果进行了拟合。由于目前尚不明确VO2薄膜的色散特性，因此将其作为一般介质材料。一般介质薄膜材料的光学常数都满足Cauchy色散模型[17]：

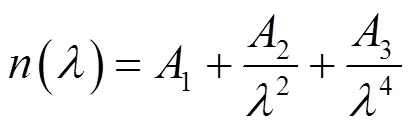
式中：1、2、3、1、2为5个相互独立的参量，可通过Origin的非线性拟合模块计算得到参量值。采用Cauchy色散模型，对常用的中远红外波段（2.5～15mm）VO2薄膜低温态与高温态光学常数进行拟合，结果如图5、图6所示。

图5为VO2薄膜低温半导体态光学常数的Cauchy色散模型拟合结果，其折射率()、消光系数()曲线表达式分别为：

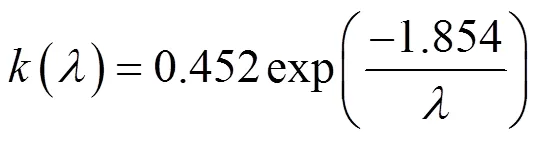
对比图2和图5可知VO2薄膜折射率低温态Cauchy色散模型拟合结果在2.5～12mm波段与单纯形法吻合程度较高而在12～15mm有较大偏差，而VO2薄膜折射率低温态Cauchy色散模型拟合结果则偏差更大，仅在2.5～4mm波段有些吻合。

如图6为VO2薄膜高温金属态光学常数的Cauchy色散模型拟合结果，其折射率()、消光系数()曲线表达式分别为：

对比图3和图6可知VO2薄膜折射率高温态Cauchy色散模型拟合结果在2.5～6mm波段与单纯形法较为吻合，其他波段明显偏离。VO2薄膜消光系数高温态Cauchy色散模型只在2.5～7mm波段接近单纯形法计算的结果。

图5 低温态Cauchy色散模型拟合结果

综合对比图2、图3、图5、图6，可以看出Cauchy色散模型在2.5～6mm中红外波段的拟合结果与单纯形法计算结果接近，但6～15mm远红外波段的结果出现较大差异，其原因与色散模型的选取有关。由于介质适用的色散模型与其物质种类关系紧密，并且与材料的吸收特性相关，根据SMT（semiconductor-metal transition）理论[18]对VO2晶体相变的解释可将VO2视为半导体态和金属态的共同体，因此其所属的物质类别就很难界定。同时由于目前无法准确表征VO2在红外波段的吸收特性，所以选择了适用于正常色散特征的Cauchy模型。通过对比结果差异可以看出：VO2薄膜在红外波段的光学特性比较复杂，在某些波段可能存在共振吸收特性。同时材料的成分属性、物理结构也是影响色散模型的因素之一，因此Cauchy色散模型无法适用于整个红外波段。在进一步研究中需根据具体情况结合其他模型来表征其光学常数，例如针对吸收特性结合Sellmeier色散模型[19]等。

4 结论

由以上仿真结果及分析可知：采用全光谱拟合方法得到的VO2薄膜折射率及消光系数等光学常数与已有的研究结果符合度较高。同时，拟合得到的VO2薄膜透射率曲线也与实测曲线基本吻合。因此，通过全光谱拟合法得到的光学常数能较准确的对VO2薄膜进行描述，可为最佳膜厚设计提供依据。通过引入Cauchy色散模型方程对全光谱拟合方法得到中远红外波段（2.5～15mm）的光学常数结果进行拟合，得到在2.5～6mm中红外波段的拟合结果与单纯形法计算结果接近，但6～15mm远红外波段则出现较大差异。因此，需要对VO2薄膜在红外波段的吸收特性进一步研究并结合其他色散模型来表征其光学常数。

[1] 李国龙, 钟景明, 王立惠, 等. 反射光谱拟合法确定聚合物半导体薄膜光学常数和厚度[J]. 激光与光电子学进展, 2016, 53(4): 043101.

LI Guolong, ZHONG Jingming, WANG Lihui. et al. Determination of optical constants and thickness of polymer semiconductor thin film with reflectivity fitting method[J]., 2016, 53(4): 043101.

[2] 章睿荣. 通过全光谱拟合法确定薄膜光学常数和厚度[D]. 杭州: 浙江大学, 2007: 4-11.

ZHANG Ruirong. Determination of optical constants and thickness of thin film with whole optical spectrum fitting[D]. Hangzhou: Zhejiang University, 2007: 4-11.

[3] 李维, 武腾飞, 王宇. 焦平面红外探测器研究进展[J]. 计测技术, 2016, 36(1):1-4.

LI Wei, WU Tengfei, WANG Yu. Progress in focal plane infrared detectors[J]., 2016, 36(1): 1-4.

[4] R E Marvel, K Appavoo, B K Choi, et al. Electron-beam deposition of vanadium dioxide thin films[J]., 2013, 111: 975-981.

[5] 陈学荣, 胡军志, 韩文政. VO2薄膜的结构、光学特性及其应用研究进展[J]. 材料导报, 2007, 21(11): 16-19.

CHEN Xuerong, HU Junzhi, HAN Wenzheng. Research progress in structures, optical characteristics and application of vanadium dioxide thin film[J]., 2007, 21(11): 16-19.

[6] 王海方, 李毅, 俞晓静, 等. 二氧化钒薄膜的变温红外光学特性研究[J]. 光学学报, 2010, 30(5): 1522-1526.

WANG Haifang, LI Yi, YU Xiaojing, et al. Study on temperature dependence of infrared optical properties of vanadium dioxide thin film[J]., 2010, 30(5): 1522-1526.

[7] 乔明霞. 薄膜光学常数和厚度的透射光谱法测定研究[D]. 成都: 四川大学, 2006: 1-6.

QIAO Mingxia. Study on determination of optical constants and thickness of thin films by transmission spectrum method[D]. Chengdu: Sichuan University, 2006: 1-6.

[8] 王盼盼, 张云龙, 吴岭南, 等. W掺杂VO2薄膜的椭圆偏振光谱表征[J]. 硅酸盐学报, 2016, 44(3): 464-468.

WANG Panpan, ZHANG Yunlong, WU Lingnan, et al. Spectroscopic ellipsometry characterization of tungsten-doped vanadium oxide films[J]., 2016, 44(3): 464-468.

[9] 杨天新, 邹豪, 王雷, 等. 棱镜耦合法确定条形波导的渐变折射率分布[J]. 中国激光, 2010, 37(3): 689-695.

YANG Tianxin, ZOU Hao, WANG Lei, et al. Determining the graded - index profiles of channel wave guides by prism coupling method[J].2010, 37(3): 689-695.

[10] 周天宇. 光学薄膜反演软件的研制与应用[D]. 长沙: 国防科学技术大学, 2010: 6-15.

Zhou Tianyu. Design and application of software of reverse engineering of optical coating[D]. Changsha: National University of Defense Technology, 2010:6-15.

[11] 夏志林, 薛亦渝, 赵利, 等. 基于包络线法的薄膜光学常数分析[J]. 武汉理工大学学报: 信息与管理工程版, 2003, 25(5):73-76.

XIA Zhilin, XUE Yiyu, ZHAO Li, et al. Analysis of thin film's optical parameters based on the envelope method[J].:, 2003, 25(5): 73-76.

[12] 李凯朋, 王多书, 李晨, 等. 光学薄膜参数测量方法研究[J]. 红外与激光工程, 2015, 44(3): 1048-1052.

LI Kaipeng, WANG Duoshu, LI Chen, et al. Study on optical thin film parameters measurement method[J].,2015, 44(3): 1048-1052.

[13] Y. Laaziza, A. Bennouna, N. Chadburn. Optical characterization of low optical thickness thin films from transmittance and bak reflectance measurements[J]., 2000, 372: 149-155.

[14] 曹治国, 汪勇. 基于模拟退火- 单纯形法的目标函数的优化[J]. 华中科技大学学报: 自然科学版, 2005, 33(6): 67-69.

CAO Zhiguo, WANG Yong. Optimization of the object function for image registration based on simulated annealing - simplex method[J].:, 2005, 33(6): 67-69.

[15] 宋婷婷, 何捷, 孟庆凯, 等. 二氧化钒的电子结构及光学性质的计算[J]. 光散射学报, 2008, 20(2): 194-199.

SONG Tingting, HE Jie, MENG Qingkai, et al. Calculation of electronic structure and optical properties of VO2[J]., 2008, 20(2): 194-199.

[16] XIAO D, Kim K W, Zavada J M. Electrically programmable photonic crystal slab based on the metal-insulator transition in VO2[J]., 2005, 97(10): 106102 (1)-(12).

[17] 闫威. 某些非线性色散方程的确定性与不确定性[D]. 广东: 华南理工大学, 2011: 28-35.

YAN Wei. Certainty and uncertainty of some nonlinear dispersion equation[D]. Guangdong: South China University of Technology, 2011: 28-35.

[18] 徐凯, 凌永顺, 路远, 等. 二氧化钒的相变机理研究进展[J]. 材料科学与工程学报, 2014, 32(4): 602-606.

XU Kai, LING Yongshun, LU Yuan, et al. Recent progress of theoretical research of VO2phase transition[J]., 2014, 32(4): 602-606.

[19] 王盼盼, 章俞之, 彭明栋, 等. VO2薄膜 Vis-NIR及NIR-MIR椭圆偏振光谱分析[J]. 物理学报, 2016, 65(12): 127201-1-127201-8.

WANG Panpan, ZHANG Yuzhi, PENG Mingdong, et al. Spectroscopic ellipsometry analysis of vanadium oxide film in Vis-NIR and NIR-MIR[J]., 2016, 65(12): 127201-1-127201-8.

Optical Constants of VO2Thin Films Based on Whole Optical Spectrum Fitting

HOU Dianxin1,2,3，LU Yuan1,2,3，SONG Fuyin1,2,3

(1.,230037,;2.,230037,;3.,230037,)

In order to measure the optical constants of VO2thin films, a whole optical spectrum fitting method is proposed in this paper. Firstly the admittance matrix method is used to derive the function of the transmittance “T”, the film thickness “D”, refraction rate “n” and extinction coefficient “K”. Secondly, the simplex method is used to optimize this function. Finally, MATLAB programming method is used for whole optical spectrum fitting of infrared transmittance of VO2thin films at low temperature and high temperature state. Then the fitting curves of the optical constants of VO2thin films, such as refractive index and extinction coefficient, are obtained. The results show that the fitting curves are in agreement with the existing research results and the measured curves. The optical constants obtained by the whole spectrum fitting method can be used to describe the VO2thin films accurately, providing the basis for the optimum design of film thickness. Furthermore, in order to describe the optical constants of VO2thin films more easily, the Cauchy dispersion model equation is also introduced in this paper to fit the optical constants of mid far infrared wave band (2.5-15mm) which was obtained by the whole spectrum fitting method.

film optics，VO2thin films，whole optical spectrum fitting，simplex method，Cauchy dispersion model

TB321

A

1001-8891(2017)03-0243-07

2016-08-24；

2016-12-21.

侯典心（1993-），男，硕士生在读，主要从事红外光学材料方面的研究。E-mail：1911240818@qq.com。

路远（1971-），男，博士，教授，主要从事光电工程方面的研究。E-mail：luyuanmail@163.com。

脉冲功率激光技术国家重点实验室主任基金资助项目（SKL2013ZR03）。