山区河流防洪避难逃生系统研究
范 强, 田 忠,唐南波,丁 灿
(四川大学水力学与山区河流开发保护国家重点实验室,成都 610065)
洪水灾害对人类的严重影响由来已久,就灾害发生的时空范围、强度以及对人类生存与发展的威胁程度而言,洪水灾害居各种自然灾害之首。我国是一个多山地国家,山区面积占到了国土陆地总面积的2/3[1]。山区河流因其具有独特的特点,在暴雨期汇流速度快,能在较短时间内形成大规模洪水,而且山区河流汇流过程难以监测,形成洪水后留给下游及两岸洪泛区居民撤离转移的时间非常短。因此,撤离工作的成功与否,关键在于能否制定出合理有效的撤退计划以及在计划实施过程中对突发事件的应对能力。
针对山区河流水头高、落差大、破坏力强的特点,在研究防洪避难逃生系统时要充分考虑下游居民短时间内的避难效果。洪水来临时,为高效、有序地疏散淹没区内的灾民,在综合分析避难逃生过程中各影响因素的基础上,对山区河流的防洪避难逃生系统进行了研究,并提出了科学规划防洪避难安置点的选址原则与安置点内的人口优化方法。
1 防洪避难系统
本研究选用动态规划中的最优控制方法[2],为洪水淹没区内的居民避难设计了相对最优的避难路径。选用的目标函数使得避难路径最短,相对而言,实施避难时最为省时。
1.1 点线结合型防洪避难模型
点线结合型洪灾分析方法是在洪水淹没范围模拟计算的基础上,确定出需要转移的居民点及避难点。由于山区乡镇的地势、人口及道路情况差别往往较大,因此在设计防洪避难系统时不能单纯的把各村庄、避难点看作点,而应看作具有不同容量的点;道路上分布着撤退的居民、车辆、牲畜等,也不能单纯的把各条道路看作线,而应看作具有不同输运能力的线。因此,根据淹没区各村庄的地理位置关系,以及各村庄的道路分布情况,以靠近道路的特征点来代表该村庄,以道路网密度作为淹没区的输运指标。道路网密度高说明道路密集,有利于该村庄的人员及物资转移撤离。
对于淹没区内的居民点,其达到避难点的最优路径属于不固定的最优路线问题,因而选用函数空间迭代法模型[3]进行求解,原理如下:
给定点集G,其个数为N,记为G={1,2,…,N},任意2点i,j之间用弧段连接,长度记为lij,0 (1) 令: (2) 作为初始函数f1(i),1 (3) 式中:fk(i)表示由i点出发最多经过k个点的最短路径(不一定到达N点)。 可证得式(1)、(2)、(3)确定的函数列{fk(i)}单调递减,且收敛于f(i)。f(i)为式(1)的解,{fk(i)}不超过N-1步收敛于f(i)。 具体到淹没区村庄居民的避难问题,将已确定的各村庄特征点及各条道路连接成网状,各道路之间的交叉点以及各村庄均作为节点考虑,则可很直观地将节点之间的距离视为上述各式中的lij。因此,一旦确定了各避难方案中的具体避难点后,就可按上述递推原理一一求出各点到达避难点的最短距离。 在实际避难逃生过程中,计算从淹没区居民点到避难点之间的最佳撤离路线,不仅要计算多点间在交通顺畅的道路网中的最短距离,也要考虑灾害发生后,洪水对道路通行能力的影响。如果洪水冲垮道路网中的某几段道路,或者有些道路因洪水淹没造成路段积水,都会使得避难人群及车辆的通行能力下降。 目前最短路径的算法中,最经典也是运用最成熟的算法是Dijkstra提出的按路径长度依此递增的最短路径法。Dijkstra算法[4]适用于所有弧的权重为非负的最短路径算法,可以给出从某定点到途中其他所有顶点的最短路径。Dijkstra算法的基本思想是标记源点到已知点的最短路径,再依次寻找另一个点的最短路径。其主要特点是以起始点为中心向外层扩展,直到扩展到终点为止,见图1。 若已知图1中对总长度最接近于定点s的m个顶点,以及从定点s到这些顶点中每一个顶点的最短路径,对定点s和这m个定点标记。然后从最接近于s的m+1个顶点可求之如下:对于每一个未着色的顶点y,考虑所有已着色顶点x,将弧(x,y)接在从s到x的最短路径后面。这样,就构成了从s到y的最短路径。 从s到某一个未着色的顶点使它按以上所述算出的路径最短,则这个顶点就是最近接于s的第m+1个顶点。因为所有弧的长度都是非负值,所以从s到最接近于s的第m+1个顶点的最短路径必然只是用所得的顶点作为其中间顶点。所以,如果最接近于s的m个顶点为已知,则第m+1个顶点可按上述方法确定。从m=0开始,将这个过程重复下去,直至求得从s到t的最短路径为止。 路径分析是防洪避难系统中最基本的功能,路径最短寻优是一种静态寻优,与实时的道路交通状况无关,只与淹没区道路网有关;时间最短寻优是一种动态寻优,与实时交通状况有着密切的联系。行程时间最短寻优是一种动态寻优,通常随着道路网中流量的变化而变化,当道路网中某段路不能正常通行时就会动态计算出其他可行的疏散路径,重新规划疏散方案。 动态路径分析模型是在路权模拟的基础上进行的。该模型随着模拟的时间进程,动态记录各路段上的交通负荷。一旦交通负荷发生变化,立即调用路权模型计算新的路权,并对路段的阻力进行更新,从而达到动态分析交通状况的效果。 车辆行驶的自由程度与相近车辆的距离有关,正常情况下,当相近的两车距离越大,其干扰度越小,车辆行驶的自由程度就越高。基于这样的认识,利用随机度来表示车辆自由行驶的程度,即: (4) 式中:R为车流随机度;n为车辆总数;f(hi)为车间影响函数[5]。 f(hi)可表示为: (5) 式中:hi是车辆间距;h0为车辆互补影响的临界车距;hmin是车辆保持安全行驶的最小车距;当hi≥h0时,f(hi)=0;当hi 根据各时段的车距情况,可将路网预警水平划分成4个等级,分别为:通畅、一般通畅、一般拥堵、拥堵,不同预警水平用不同的信号灯表示,各信号灯含义如下: “绿灯”:当0.8 “黄灯”:当0.5 “黄灯闪烁”:当0.2 “红灯”:当0 以道路网数据为基础,利用路阻函数模型计算出各时段的路权。在此基础上,根据预警系统判断出该道路的预警级别,当道路处于“畅通”、“一般畅通”状态时,车流及人群撤离迅速,不需要调用路阻函数计算新的路权。当预警级别为“一般拥堵”、“拥堵”状态时,车流及人群撤离受阻,需要调用路阻函数计算新的路权,并对道路网数据库进行修正更新,从而得到实时的道路信息数据,从而实现对灾民撤退全过程的动态跟踪模拟。 山区避难场所的选择应引入科学的规划方法进行布局,使有限的安全保障资源最大限度地为灾民提供避难服务。避难场所应选择地势较高、交通较为便利处,所属的配套设施应尽可能齐备,包括:避难生活设施、指挥和通信设施、疏散保障设施、医疗救护设施及运输场地设施等[6,7]。 避难场所的规划选择及空间配置,应充分考虑以下原则。 (1)综合防灾,统筹规划,将避难点的选择作为一个系统性工程,要充分考虑到避难点之间的人员、物资转移情况。 (2)与山区平整地规划相协调,在功能上要实现平、灾结合。 (3)因地制宜,选址安全,要确保避难点不受洪水侵袭,不能让灾民多次搬迁。 (4)避难点高程选择不能太高,其地面高程只要高于“洪水位+安全超高”即视为安全,这样既方便建设,也方便救灾物资的运输。 (5)受灾人员需合理安置,不能简单就近安排,安置点具有一定容量,不能无限制接纳灾民。 (6)明确救灾点及责任区区划,以确保发生洪水时相关防灾机构能及时指挥灾民撤离。 (7)应急避难与长期防灾相结合,明确避难场所的分类分级,根据人口分区,将避难点分为临时聚集点、临时避难点、永久避难点3级。 (8)避难场所可持续发展的关键是要与避难场所的资源承载能力相协调,要控制好安置区内的人口数量,使人口维持在资源承载力所能接受的范围之内。 避难安置区地势较高,有效抵御了洪水侵犯,安置区的道路便于人员、物资进出,这种现象可以用界壳理论[8]来分析。界壳理论是研究系统周界的一般性理论,它从全新的观点来讨论系统的平衡问题。界壳被定义为处在系统外围能卫护本系统,且与环境进行交换的中介体,它是系统的周界,是系统的一部分。避难安置区系统的界壳处在安置区系统和外围的交界处,由界壁及界门组成。安置区系统界壳的界壁主要为系统的边缘周 界,如河岸、堤坝等;系统界壳的界门主要为堤、坝的闸门和通往外界的道路等。安置区的人口变化与移民控制是一个典型的界壳论问题,移民的交换律可以简单地表示为: α=(Iin+Iout)/2 (6) 式中:Iin为移入率;Iout为移出率。 人口的动态变化可以用指数函数来表示,为使安置区内的人口不超过安置区的承载力,规定当人口增量超过某一值c0时停止灾民进入,这样的模型可表示为: (7) 式中:Δx/Δt为t时段内进入安置区的人数;k为该安置区的安置系数。 这里δ起到开关函数的作用,当Δx/Δt≤c0时,δ=1;当Δx/Δt>c0时,δ=0。即当δ=1时,灾民可继续进入该安置区;当δ=0时,该安置区达到该安置区安置能力的上限,灾民需进入其他安置区避难。 盐边县位于四川省凉山州西部,隶属于攀枝花市,是二滩水电站库区的主要淹没县。全县面积3 344 km2,辖4个镇,12个乡,164个村和7个居民委员会,总人口20.19万人;成昆铁路横贯境内,雅攀高速公路通过县境。盐边县地势北高南低,由西北向东南倾斜,为我国西南部山区典型的山区城市,在洪水期极易受到山区洪水的侵袭。 二滩水电站位于雅砻江下游,坝高240 m,总库容58 亿m3。当雅砻江流域进入汛期后,若暴雨产生的大洪水迅速从上游传至二滩库区,且来水量超过二滩库区的防洪库容,为避免因超标洪水造成的溃坝淹没攀枝花市区,必须进行紧急泄洪。 下泄洪水与雅砻江原河道上涨河水迅速向下游传播,盐边县首当其冲,二滩坝址距盐边县城北32 km,经洪水演算分析:盐边县城应急转移时间为35 min;盐边县城位于雅砻江左岸,最近距离500 m,此时需将县城5.2万人口迅速进行转移至距雅砻江河道5 km外的避难安置点。 根据盐边县城的人口分布、建筑物布局及路网状况将县城划分为7个区,选取各区内靠近转移道路的居民点作为代表点,根据各区内的道路分布情况将它们分成7个转移点。为简化计算,假定淹没区域内的所有道路属性一致。淹没区分区、洪水淹没情况及避难安置点的分配见图2。 图2 避难逃生示意图Fig.2 Schematic diagram of evacuation escape 利用Dijkstra法计算出最短路径和最短迁移距离,根据淹没区路网某时刻的路阻函数,利用动态路径分析模型,能够计算出撤退过程中路网的路权,最后计算出最短的迁移时间,研究结果见表1。 表1 盐边县城防洪避难决策方案指标Tab.1 Yanbian County flood refuge decision-making index 灾民撤退与安置的第1要求是确保转移人员的生命安全,在撤退过程中要尽量避免各转移点同时选择同一道路撤退而造成交通拥堵。因此,在撤退过程中要妥善安排各分区的出发顺序,以避免发生拥堵,影响撤退速度。 在灾民进入安置区后,要充分重视安置区的人口优化配置,在某安置区达到安置能力上限时,应及时组织灾民撤往其 他备用安置区。为保证安置区的可持续发展,应充分论证安置区的生态系统能否承载相应的灾民人数,以确保该安置区的永续利用。 本研究选用动态规划中的最优控制方法,为洪水淹没区的居民设计了相对最优的避难路径。并以盐边县城作为实例进行了防洪避难系统的研究,研究结果表明,本文所建立的模型可以有效解决淹没区灾民撤的退问题。防洪避难系统的研究和开发在我国刚刚起步,本研究所建立的模型仍处于基础研究阶段,在接下来的研究中将综合考虑更为复杂的各项因素,使洪灾避难系统更臻完善。 □ [1] Li Fawen. Study on the theory and application of flood disaster evacuation decision[D].Nanjing: College of Water Resource and Environment, Hohai University, 2005. [2] 谢林柏, 赵维一, 纪志成.基于δ算子的网络控制系统最优控制方法[J].东南大学学报, 2006,36(增刊). [3] 何少苓, 刘树坤,廖文根,等.防洪避难系统在东平湖滞洪区的运行[J].水利学报, 1994,(10):36-39. [4] Zhan F B. Three fastest shortest path algorithms on real road networks[J].Journal of Geographic Information and Decision Analysis, 1997,1(1):69-82. [5] 杨佩昆, 黄文忠. 城市道路车队离散过程中的交通流模型[J].同济大学学报, 1994,9(3):294-299. [6] Yao Qinling. Urban calamity decrease layout[J].Urban Layout, 1995,(3):39-40. [7] 苏幼坡, 刘瑞兴. 城市地震避难场的规划原则与要点[J].灾害学, 2004,19(1):87-91. [8] 曹鸿兴.系统周界的一般理论——界壳论[M]. 北京:北京气象出版社, 1993.1.2 Dijkstra算法求解最短路径
1.3 防洪避难路阻函数计算模型
2 避难场所的选择
3 安置区人口的优化
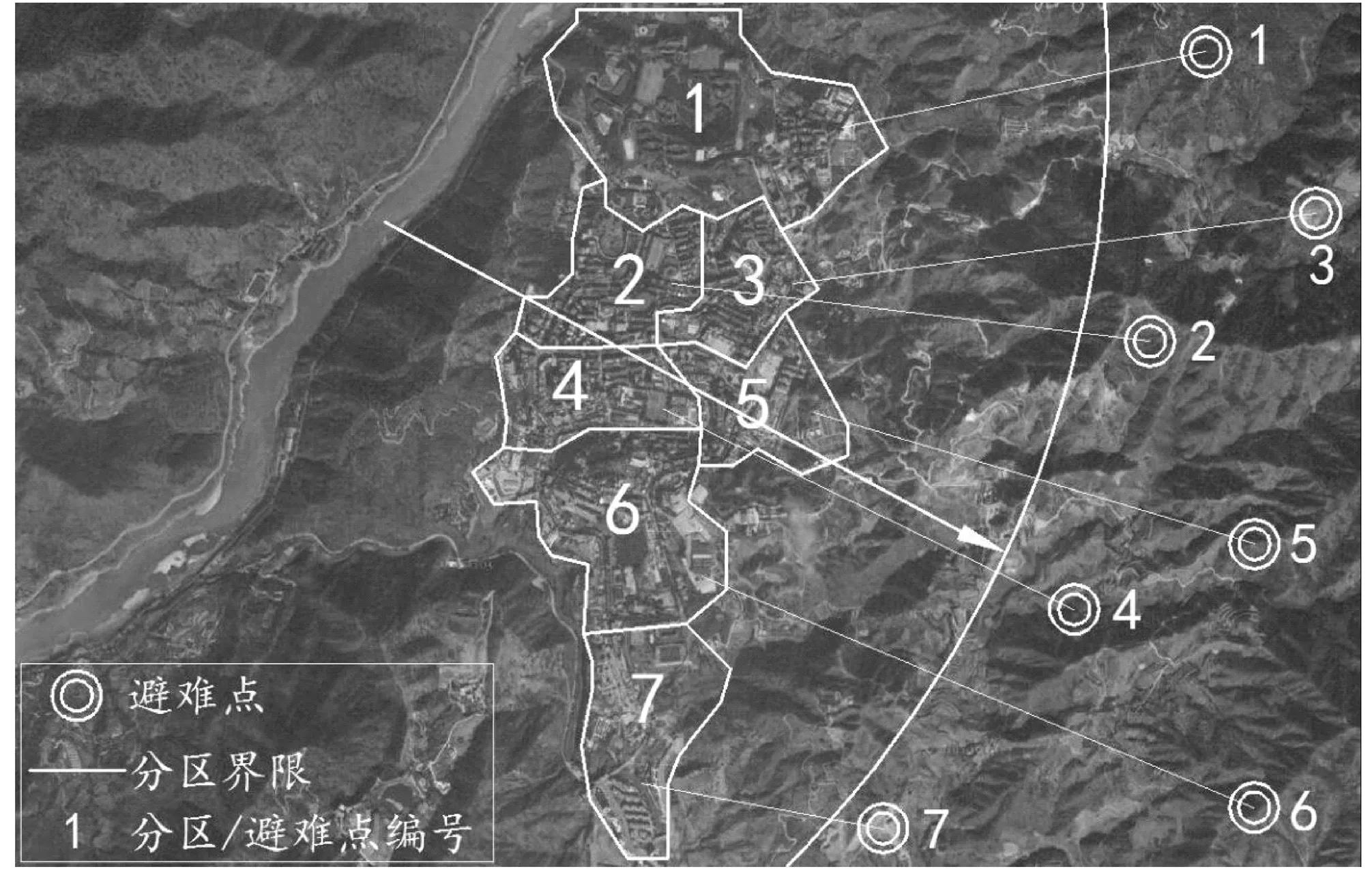
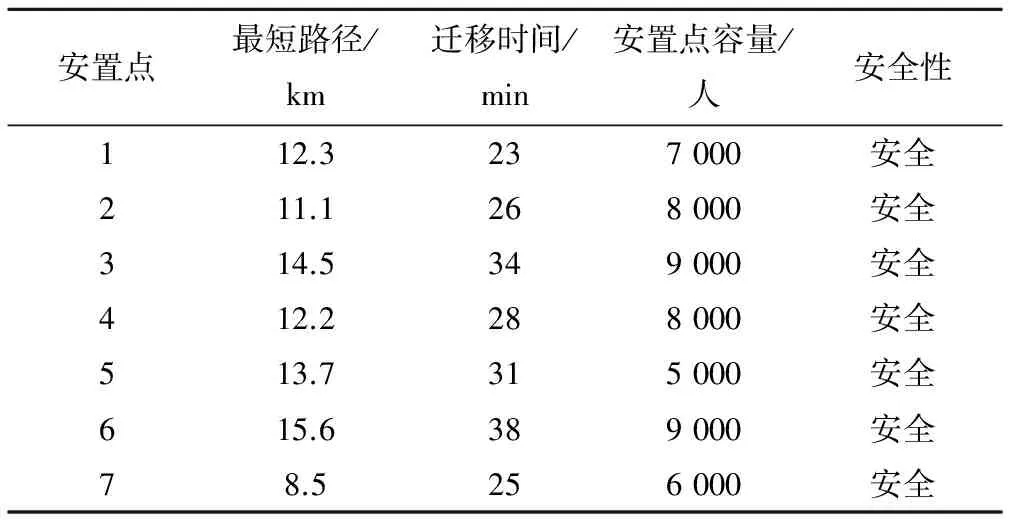
4 应用实例
5 结 语

