用数值方法求解离心泵运行工况点

王晓敏，朱满林，李小周，常金梅

(西安理工大学西北旱区生态水利工程国家重点实验室培育基地，西安 710048)

水泵工况点是指水泵在某一瞬时的实际工作参数，包括流量Q、扬程H、轴功率N、效率η等。水泵基本性能曲线由流量与扬程曲线(Q～H)、流量与效率曲线(Q～η)和流量与轴功率曲线(Q～N)等组成。正确确定水泵工况点是水泵优化选型、泵站优化设计以及泵站安全经济运行的必要条件。

确定水泵工况点的方法有图解法和数解法。图解法确定水泵工况点，是将水泵的流量与扬程曲线(Q～H)、装置需要扬程曲线(Q～Hr)绘制在同一坐标系，找其交点得到水泵工作流量Q和扬程H，然后由水泵的基本性能曲线得到水泵的轴功率N和效率η等参数。图解法概念清楚，但确定复杂供水系统水泵工况点比较麻烦。数解法确定水泵工况点，是根据水泵输水系统装置，列求解水泵工况点方程组，然后求解[1-3]。由于离心泵内部结构复杂，目前还没有能够准确描述离心泵流量与扬程性能曲线的方程形式供大家采用，所以用数解法确定水泵工况点时，可以采用数据拟合或插值的方法。对离心泵流量与扬程性能曲线的拟合方程多采用抛物线形式[4-5]，也有采用高次多项式[6-8]。显然若采用的离心泵流量与扬程性能曲线的拟合方程形式不同，计算的结果会有差异。插值的方法在水泵工况点的求解中应用较少，Bruce E. Larock等对水泵流量与扬程特性曲线(Q～H)方程用二次多项式表示，采用二次拉格朗日插值法求解其系数，进而求解水泵工况点[9]。拉格朗日插值多项式的优点是格式整齐规范，它的缺点在于当需要增加插值节点时，拉格朗日基函数都要随之发生变化，不得不重新计算。而且如果测试点数量较多时，插值多项式次数较高，易发生Runge现象，不一定能得到较好的结果[10]。

从水泵厂家提供的水泵性能曲线上找若干离散点，非离散点的水泵性能参数采用三次样条插值获得，以此对其流量与扬程性能曲线(Q～H)进行描述。采用数值方法计算，MATLAB编程确定离心泵工况点。

1 单台离心泵运行工况点

图1为单台离心泵装置及其工况点求解原理图。

图1 单台离心泵装置及其工况点求解原理Fig.1 Single centrifugal pump device and the calculating schematics of operating point

列求解水泵工况点方程组：

H=H(Q)

(1)

Hr=Hst+SQ2

(2)

H=Hr

(3)

式中：H为水泵扬程， m；Hr为装置需要扬程，m；Q为水泵流量,m3/s；Hst为装置静扬程，m；S为管道阻力参数，s2/m5。

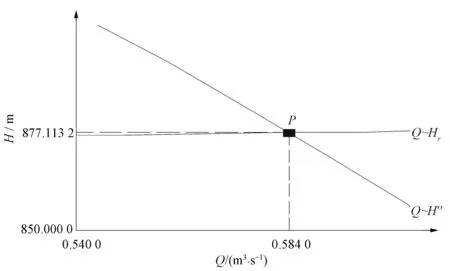
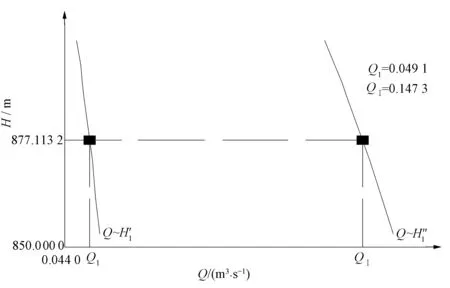
式(1)为用离散点表示的离心泵流量与扬程性能曲线，可从水泵厂家提供的水泵性能曲线上找n个点得到，即(Qi,Hi)(i=1,2,…,n),其中Q1

根据式(1)、(2)和(3)可构造函数：

F(Q)=H(Q)-Hst-SQ2=0

(4)

式(4)只有一个未知数Q，但由于离心泵流量与扬程性能曲线H=H(Q)为离散点，不能直接求解，可采用二分法求解。若F(Q1)F(Qn)>0则说明水泵工作流量不在区间[Q1,Qn]，应当重新选择水泵。

2 离心泵并联运行工况点

图2所示为2台不同型号离心泵并联运行。

图2 离心泵并联装置Fig.2 Device of centrifugal pump in parallel

列求解水泵工况点方程组：

EC=H1+Z1-SACQ21

(5)

EC=H2+Z2-SBCQ22

(6)

EC=Z+SCDQ2

(7)

Q=Q1+Q2

(8)

H1=H1(Q1)

(9)

H2=H2(Q2)

(10)

式中：EC为C点能量，m；H1、H2为泵P1、P2的扬程，m；Q1、Q2、Q为泵P1、P2流量及总流量，m3/s；Z1、Z2、Z为吸水池1、2及出水池的水位高程，m；SAB、SBC、SCD为AC、BC、CD段管道的阻力参数，s2/m5。

式(9)和(10)为用离散点表示的泵P1、P2流量与扬程性能曲线。设泵P1和P2的流量与扬程性能曲线离散点个数分别为m和n，即泵P1和P2的流量范围分别为[Q11,Q1m]和[Q21,Q2n]。

构造函数

F1(Q1,EC)=H1(Q1)+Z1-SACQ21-EC=0

(11)

F2(Q2,EC)=H2(Q2)+Z2-SBCQ22-EC=0

(12)

(13)

具体求解步骤如下：

(1)确定EC的取值范围。将Q11和Q1m分别代入式(11)得EC的取值范围EC1，将Q21和Q2n分别代入式(12)得EC的取值范围EC2，则EC的取值范围应为EC1和EC2的交集EC12。设EC12=[ECmin,ECmax]，若EC12为空集，则表明水泵选择不合理，应重新选泵。

(2)将ECmin分别代入式(11)和(12)，采用二分法可以求出Q1(ECmin)和Q2(ECmin)，将Q1(ECmin)和Q2(ECmin)代入式(13)得F(ECmin)。同样将ECmax分别代人式(11)和(12)，采用二分法可以求出Q1(ECmax)和Q2(ECmax)，将Q1(ECmax)和Q2(ECmax)代入式(13)得F(ECmax)。若F(ECmin)F(ECmax)>0,则说明水泵选择不合理，应重新选泵，否则可以采用二分法求得EC。

(3)将求得的EC分别代入式(11)和(12),采用二分法求得泵P1、P2的工作流量Q1和Q2。将Q1和Q2分别代入式(9)和(10)，可求得泵P1、P2的工作扬程H1和H2。

3 离心泵串联运行工况点

图3所示为2台不同型号离心泵串联运行。

图3 离心泵串联装置Fig.3 Device of centrifugal pump in series

列求解水泵工况点方程组：

H1=H1(Q)

(14)

H2=H2(Q)

(15)

H1+H2=Hst+SQ2

(16)

式中:Q为水泵流量，m3/s；其他符号意义同前。

由式(14)、(15)和(16)可构造函数:

F(Q)=H1(Q)+H2(Q)-Hst-SQ2=0

(17)

设泵P1、P2的流量与扬程性能曲线离散点个数分别为m和n，即泵P1、P2的流量范围分别为[Q11,Q1m]和[Q21,Q2n]，[Q11,Q1m]和[Q21,Q2n]的交集[Qmin,Qmax]即为水泵工作流量的取值范围。

由于离心泵流量与扬程性能曲线为离散点，不能直接求解，可采用二分法求解式(17)，得到2台泵的工作流量Q。若F(Qmin)F(Qmax)>0,则说明水泵工作流量不在区间[Qmin,Qmax]，应当重新选择水泵，否则用二分法求解Q。

将Q分别代入式(14)和式(15)，可以求得泵P1、P2的工作扬程。

4 算 例

某供水工程取水泵站由4口大口井组成，每口井安装3台潜水泵，3台水泵对称布置。正常工作时共12台同型号潜水泵并联运行，见图4。分别用数值方法和图解法对水泵工况点进行求解。

4.1 用数值方法求解水泵工况点

列求解水泵工况点方程组:

EM=H1+Z1-3Q1/q1-S0Q21-SAM(3Q1)2

(18)

EM=H2+Z2-3Q2/q2-S0Q22-SBM(3Q2)2

(19)

EM=H3+Z3-3Q3/q3-S0Q23-SCM(3Q3)2

(20)

EM=H4+Z4-3Q4/q4-S0Q24-SDM(3Q4)2

(21)

图4 某供水工程示意Fig.4 Schematic view of a water supply project

(22)

Q=3 (Q1+Q2+Q3+Q4)

(23)

H1=H1(Q1)

(24)

H2=H2(Q2)

(25)

H3=H3(Q3)

(26)

H4=H4(Q4)

(27)

式中：EM为M点能量，m；H1、H2、H3、H4为1～4号各井内泵的扬程，m；Z1、Z2、Z3、Z4、Z为1～4号各井内静水位及出水池的水位高程，；Q1、Q2、Q3、Q4、Q为1～4号各井内单泵的流量及总流量，m3/s；q1、q2、q3、q4为1～4号各井内的单位出水量，m3/(s·m)；S0、S为A1A、A2A、A3A、B1B、B2B、B3B、C1C、C2C、C3C、D1D、D2D、D3D和MM1、MM2段管道的阻力参数，s2/m5;SAM、SBM、SCM、SDM分别为各下标对应管段的阻力参数，s2/m5。

式(24)～(27)为用离散点表示的1～4号各井内泵流量与扬程性能曲线。由于是同型号潜水泵并联运行，1～4号各井内泵的流量与扬程性能曲线离散点相同，即各井内泵流量范围相同。

构造函数：

F1(Q1,EM)=H1(Q1)+Z1-3Q1/q1-

S0Q21-SAM(3Q1)2-EM=0

(28)

F2(Q2,EM)=H2(Q2)+Z2-3Q2/q2-

S0Q22-SBM(3Q2)2-EM=0

(29)

F3(Q3,EM)=H3(Q3)+Z3-3Q3/q3-

S0Q23-SCM(3Q3)2-EM=0

(30)

F4(Q4,EM)=H4(Q4)+Z4-3Q4/q4-

S0Q24-SDM(3Q4)2-EM=0

(31)

Q2(EM)+Q3(EM)+Q4(EM)]=0

(32)

具体求解如前述离心泵并联运行工况点求解步骤，从潜水泵性能曲线上读得Q、H数据列于表1，各段管阻力参数列于表2，出水池水位Z,及各井内静水位Z1、Z2、Z3、Z4列于表3，各井内单位出水量列于表4，采用MATLAB编程计算结果见表5。

表1 潜水泵流量扬程数据Tab.1 The data of submersible pump head-discharge

表2 各段管阻力参数 s2/m5

表3 出水池及各井内静水位 m

表4 各井内的单位出水量 m3/(s·m)

表5 4口井并联运行单泵工况点Tab.5 Single pump operating point of 4 wells in parallel

4.2 用图解法求解水泵工况点

用AutoCAD制图，将潜水泵流量扬程曲线Q～H绘于图5。

图5 潜水泵流量扬程曲线Q～HFig.5 The submersible pump head-discharge curve Q～H

如图4所示，将泵的出口延伸到并联点M,泵的进口延伸到绝对高程0点，也就是将并联点前的管路阻力损失当成泵内水力损失，则每口井内假想单泵并联运行时的扬程分别为：

H′1=H1+Z1-3Q1/q1-S0Q21-SAM(3Q1)2

(33)

H′2=H2+Z2-3Q2/q2-S0Q22-SBM(3Q2)2

(34)

H′3=H3+Z3-3Q3/q3-S0Q23-SCM(3Q3)2

(35)

H′4=H4+Z4-3Q4/q4-S0Q24-SDM(3Q4)2

(36)

由于每口井3台假想泵具有相同的扬程，因此可以采用等扬程下流量横加的方法得到各井3台泵并联运行时的流量扬程曲线。以1号井为例，将式(33)绘于图6，即为曲线Q～H′1，等扬程下流量横加，得到1号井3台泵并联运行的曲线Q～H″1。用同样的方法可以分别得到2～4号井3台泵并联运行的流量扬程曲线Q～H″2、Q～H″3和Q～H″4，见图7。图7所示曲线则相当于4台假想大泵的流量扬程曲线，将其等扬程下流量横加可得到图8所示12台水泵并联运行的曲线Q～H″。在图8中同时画出装置需要扬程曲线Hr=Z+S(Q/2)2，则其与曲线Q～H″的交点P即为12台水泵并联工况点。过P点做横坐标的平行线与Q～H″1、Q～H″2、Q～H″3、Q～H″4各曲线的交点分别为P1、P2、P3和P4(见图7)，这些交点的横坐标即分别为各井内3台泵的流量QⅠ、QⅡ、QⅢ、QⅣ，其1/3就是各井内单泵工况点的流量。以1号井为例，图6中的QⅠ=0.147 3，Q1=(1/3)QⅠ=0.049 1。得到单泵流量Q1、Q2、Q3、Q4，即可在水泵Q～H曲线上找到工况点，见图5。计算表明，图解法与数值方法求解该算例水泵工况点的结果一致。

图6 1号井3台泵并联流量扬程曲线Q～H″1Fig.6 The 3 pumps in parallel head-discharge curve Q～H″1 of 1# well

图7 各井3台泵并联流量扬程曲线Q～H″Fig.7 The 3 pumps in parallel head-discharge curve Q～H″ of each well

5 结 语

提出了求解离心泵运行工况点的一种新的数值计算方法。从水泵厂家提供的水泵性能曲线上找若干离散点，描述离心泵流量与扬程性能曲线，非离散点的水泵性能参数采用三次样条插值获得。给出了离心泵运行工况点的数值方法计算步骤，采用MATLAB编程，对某供水工程取水泵站多台水泵并联运行工况点进行了分析计算，并与图解法进行了对比，结果表明提出的水泵工况点计算方法是可行的。

□

图8 12台水泵并联工况点Fig.8 The operating point of 12 pumps in parallel

[1] 刘竹溪，刘景植.水泵及水泵站[M].4版.北京：中国水利水电出版社，2009-11：120-127.

[2] 刘 超.水泵及水泵站[M].北京：中国水利水电出版社，2009- 09：54-58.

[3] 姜乃昌.泵与泵站[M]. 5版.北京：中国建筑工业出版社，2007-12：33-42.

[4] 路兵华，魏 旭. 水泵性能曲线拟合及并联运行水泵选型计算方法[J].工程建设，2014，46(3):29-31.

[5] 梁山城，夏培松. 水泵性能曲线拟合研究[J].中国农机化学报，2014,35(4):111-113.

[6] 杨伟东，余学军, 基于 MATLAB 的多角度水泵性能曲线的拟合[J].湖南农机，2011,38(7):58-59,69.

[7] 吴小平,把多铎,胡沙沙，等.基于MATLAB离心泵特性曲线的拟合与绘制[J].中国农村水利水电，2010,(11):144-146.

[8] 刘建交,把多铎, 向华琦.两种水泵性能曲线拟合方法的研究[J].水电能源科学,2012,30(2):136-138.

[9] Bruce E Larock，Roland W Jeppson，Gary Z Watters. Hydraulics of pipeline systems[M]. Boca Raton, Florida: CRC Press LCC,2000:30-33.

[10] 李庆扬.数值分析[M].北京：清华大学出版社，施普林格出版社, 2001- 08：26-30,45-46.

[11] 张智星.MATLAB程序设计与应用[M].北京：清华大学出版社，2002：330-331.