消力池内双层悬栅不同布置类型的压强特性研究

蒋健楠，牧振伟，牛 涛，位静静

(新疆农业大学水利与土木工程学院，乌鲁木齐 830052)

在消力池内布置辅助消能工，是提高消力池消能效果的常用方式[1]，但在一些多沙河流上的水利工程中，底孔出流的消力池不仅要考虑泄流消能问题，还要考虑排沙问题[2]，一些布置在消力池底板上的辅助消能工如趾墩[3]、掺气分流墩[4]、T形墩[5]等，极易受到含沙水流冲刷，不能起到较好的辅助消能作用。悬栅作为一种新型辅助消能工应用到消力池内，不易受到含沙水流冲刷，能起到较好的辅助消能作用。前人针对在消力池内布置悬栅作了一定的研究[6-8]，得到消力池内单层悬栅布置类型的取值范围，并成功应用到实际工程之中。在模型试验研究的同时，吴战营[11]、朱玲玲[12]等均对消力池内布置单层悬栅进行了数值模拟计算，得到悬栅消力池的压强分布。以上研究均是针对消力池内布置单层悬栅，且只探究了消力池内悬栅消能效果较优的布置类型，并未考虑悬栅因受含沙水流的冲刷侵蚀而结构稳定性受到影响的问题，对消力池布置双层悬栅的压强分布研究较少。结构稳定是悬栅能够在实际工程中长期使用的前提，影响悬栅结构稳定性的主要包括水流掺气侵蚀、水流冲击、泥沙的侵蚀等，其中水流的冲击破坏对悬栅结够影响较大，探究水流对悬栅的冲击破坏情况具有重要意义。压强是反映悬栅受水流冲击破坏的主要水力参数，通过数值模拟方法[9-10]，不仅能模拟全面的悬栅布置方案，还能得到详细的压强场，通过数值方法模拟水流对悬栅的冲击破坏情况，可以得到悬栅消力池内的压强分布规律。考虑到问题的复杂性，暂且忽略消力池内水流挟沙和掺气特性对压强的影响。借鉴前人数值模拟经验，本文通过改变消力池内双层悬栅的布置类型，进行数值模拟计算，探究消力池内不同布置类型的双层悬栅对压强场的影响以及受水流冲刷侵蚀的变化，为悬栅的结构设计提供依据。

1 数值模拟

1.1 数值模拟方案设计

通过在新疆五一水库模型试验得到，在消力池内布置悬栅能改善消力池的消能效果，为研究悬栅对消能效果的影响规律，需重新设计消力池尺寸；借鉴五一水库消力池尺寸的设计经验，以Q=21.43 L/s作为单宽流量设计值，通过相关水力计算[13]，得到消力池及悬栅尺寸如图1所示。参考悬栅消力池模型尺寸，建立相应的三维数学模型。通过改变消力池内双层悬栅布置类型进行数值模拟方案设计，在改变悬栅布置类型时，保持渥奇段4根和消力池前端1根悬栅位置不变，只改变消力池内悬栅水平间距b1(简称：栅距)、栅条数n以及悬栅垂直间距b2(简称：层距)。由均匀正交设计模型试验[14]可知，当栅条数n=11根、栅距b1=12 cm、层距b2=4 cm时消能效果较好，根据此试验结果，为便于计算成功分析，取双层悬栅栅条数n、栅距b1、层距b2与消力池护坦高d的比值为m1、m2、m3。

取d=10 cm；栅条数n分别取7根、11根、15根；栅距b1分别取8、10、12 cm；层距b2分别取2、3、4 cm。通过数值模拟计算双层悬栅周围的压强场，分析悬栅受水流冲侵蚀情况，具体数值模拟计算方案如表1所示。

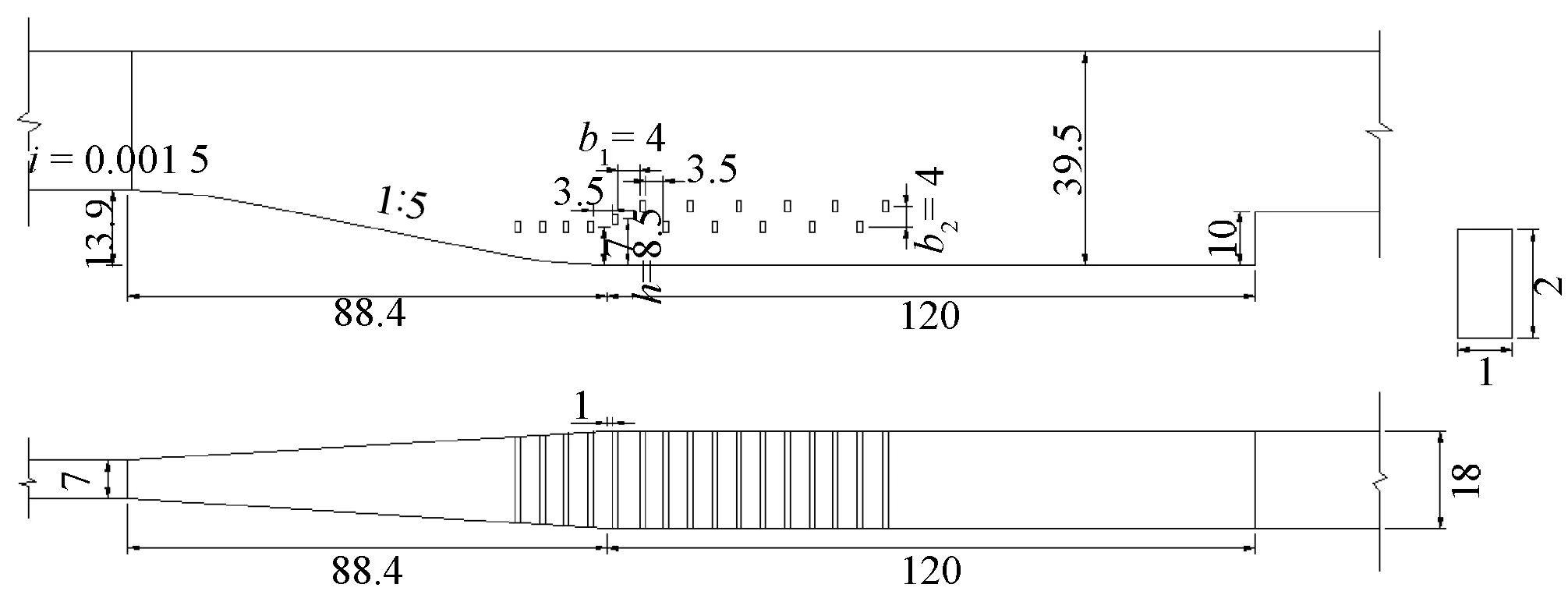
图1 悬栅消力池结构示意图(单位：cm)Fig.1 The structure arrangement of the stilling basin and the suspended grid

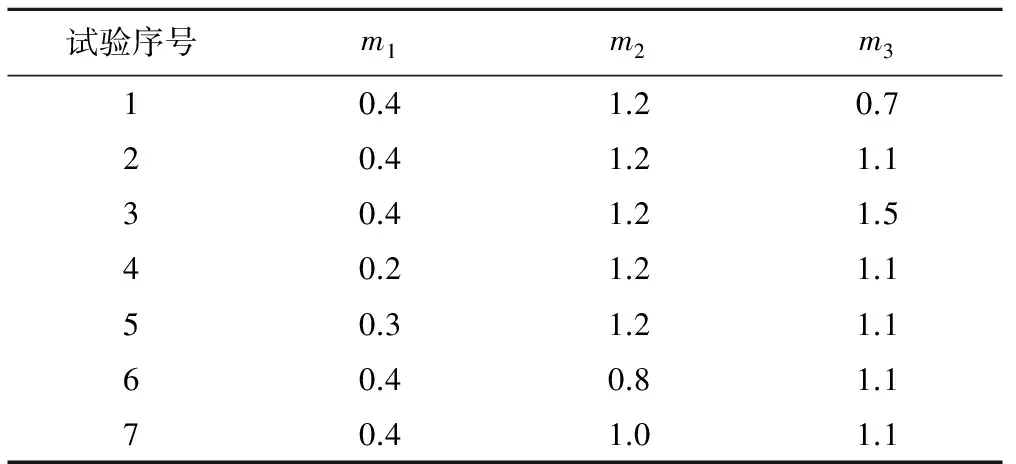
试验序号m1m2m310．41．20．720．41．21．130．41．21．540．21．21．150．31．21．160．40．81．170．41．01．1

1.2 控制方程

由于悬栅消力池内有水流旋转及旋流流动，采用由Yakhot和Orszag建立的RNGk～ε双方程紊流模型[15]，能更好地处理高应变率及流线弯曲程度较大流动，具有较高的可靠性和准确性。该紊流模型的连续方程、动量方程以及k、ε方程分别表示如下。

连续方程：

(1)

动量方程：

(2)

k方程：

(3)

ε方程：

(4)

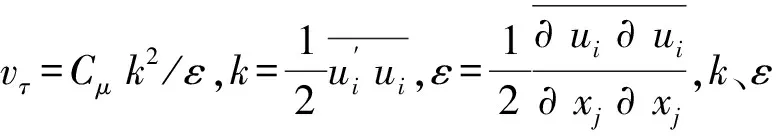
表2 各通用常数的取值Tab.2 The value of the universal constant

VOF法是处理复杂自由表面的有效办法，是目前广泛应用的追踪自由表面的数值方法[16]因此采用该模型处理自由液面。控制方程组的离散采用有限体积法，通过欠松弛迭代方法求解离散控制方程组，数值计算采用PISO算法。

1.3 网格划分与边界条件设定

数值模拟建模在对悬栅消力池进行网格划分时，均采用六面体结构化网格(见图2)，网格尺寸范围为2.0～2.5 cm；由于消力池内布置双层悬栅部分是数值模拟计算主要区域，故该区域内网格划分较密，网格尺寸范围为0.8～1.5 cm，由于不同计算方案时悬栅的栅条数、栅距以及层距均不一样，因此网格划分的疏密程度均不同，各方案模型网格总数量大约为29 000个。

在边界条件设定时，消力池进口边界采用进口速度，进口速度数值根据物理模型试验中实测流量换算而得；出口边界采用出口压力，其压强值为大气压强；上边界采用进口压力，其压强值为大气压强；湍流近壁区采用标准壁面函数进行处理，壁面采用无滑移条件。

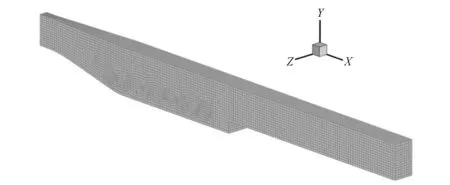
图2 网格划分示意图Fig.2 The schematic diagram of the grid division

1.4 模型验证

通过数值模拟计算得到不同悬栅布置类型的消力池内最大水深(见表3、表4)。根据数学模型计算值和物理模型试验值对比，结果表明最大水深两者误差均在9%以内(见表3)，最大水深处流速两者误差均在5%以内，数值模拟结果与模型试验结果吻合相对较好，说明该数值模拟方法能较好地模拟悬栅消力池。

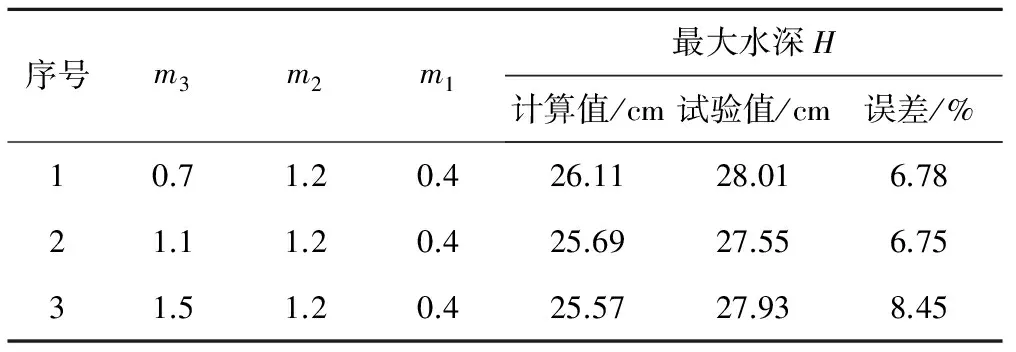
表3 消力池内最大水深及误差Tab.3 Maximum depth of the water and error in the stilling basin

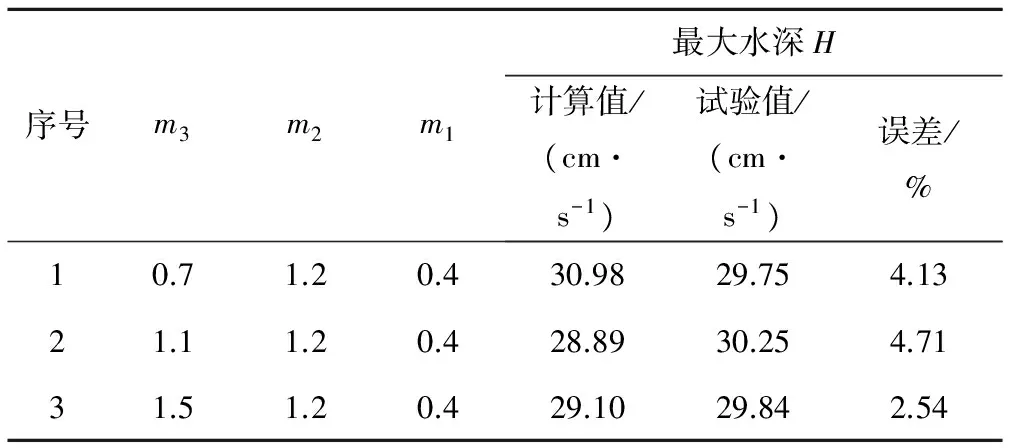
表4 消力池内最大水深处流速及误差Tab.4 Velocity at the maximum depth of the waterand error in the stilling basin

2 计算结果分析

通过数值模拟计算，得到双层悬栅不同布置类型的消力池底板以及悬栅周围的压强分布，时均压强为某一点在一段时间内瞬时总压强的平均值[17]，能较好地反应消力池底板受到水流冲刷侵蚀的情况，悬栅四面以迎水面和背水面受到水流作用

更为明显，因此以悬栅迎水面p1与背水面p2的时均压强差Δp(下面简称：压强差)来表征悬栅受到水流作用的大小，但不论压强差值是正还是负，均会对悬栅结构稳定产生影响。为便于分析，取压强差Δp的绝对值|Δp|进行数据处理，其中|Δp|由下式计算：

|Δp|=|p1-p2|

(5)

2.1 改变m1对压强场的影响

通过数值模拟计算，得到m2和m3不变，即m2取1.2，m3取1.1，m1不同取值时消力池底板的时均压强，如图3所示。消力池上游段，水流刚进入消力池时，流速较大，水流动能较大，动能水头所形成的动水压强较大，时均压强较大，无论m1取何值，相对消力池其他位置，消力池上游段底板上时均压强均较大；水流进入消力池后，由于双层悬栅作用，水流与悬栅相互碰撞掺气消能，水流流速减小，水流动能减小，动能水头所产生的动水压强减小，时均压强减小，消力池上游段底板时均压强均较小。当m1取0.2时，消力池底板的时均压强较小，但时均压强变化比较紊乱；当m1取0.4时，消力池底板时均压强与m1取0.2时接近，且时均压强变化比较平稳。

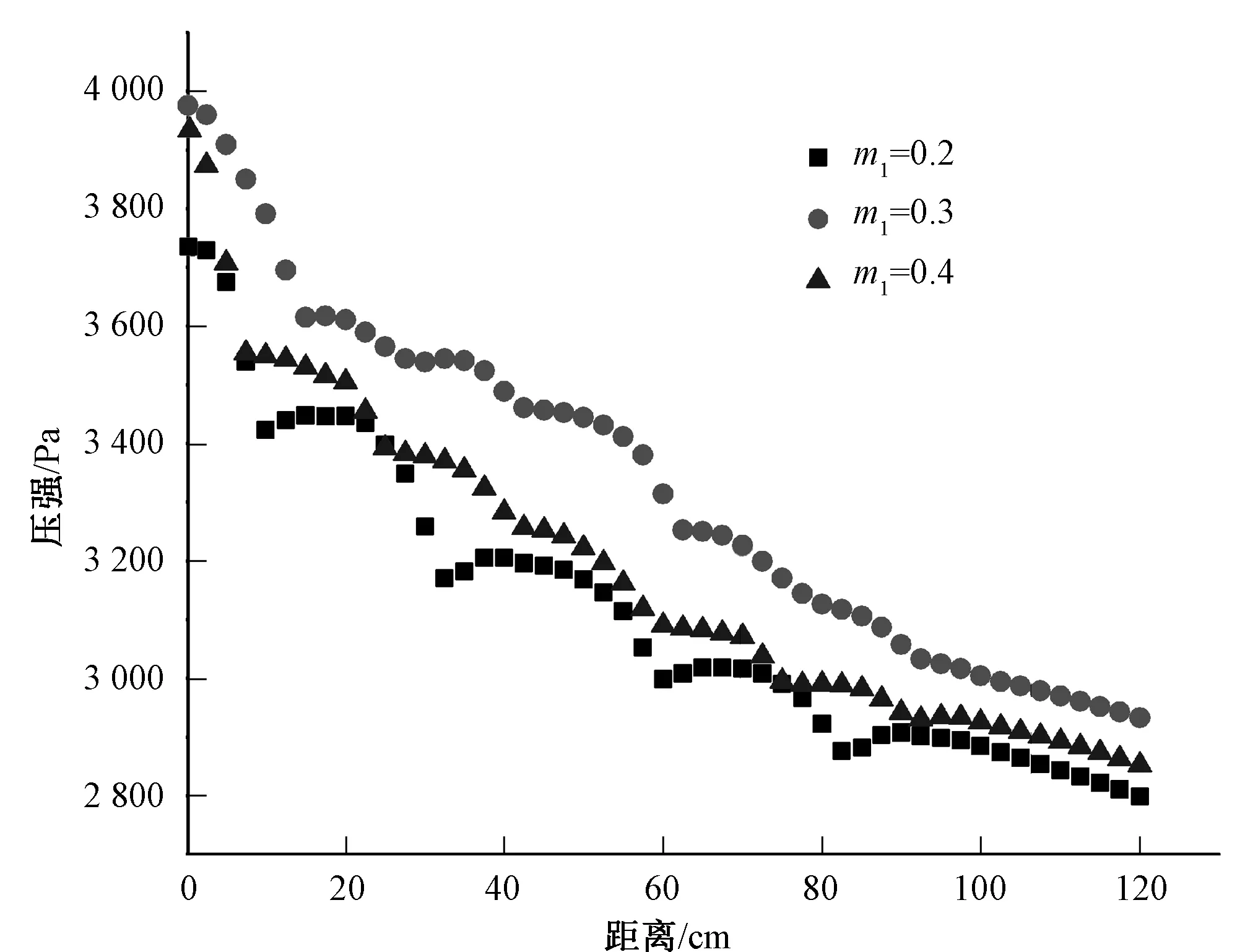
图3 m1不同取值时消力池底板时均压强Fig.3 The time average pressure of the bottom plate of the stilling basin in different value of m1

保持m2和m3不变，根据数值模拟计算，得到m1不同取值时消力池内各个悬栅时均压强差|Δp|，如表5所示。当m1取不同值时，消力池内第1根悬栅时均压强差均为最大；当m1取0.2时，最小时均压强差为3.10 Pa，在第10根悬栅处；当m1取0.3时，最小时均压强差为5.44 Pa，在第16根悬栅处；当m1取0.4时，最小时均压强差为5.06 Pa，在第12根悬栅处。

表5 不同m1时各个悬栅时均压强差|Δp| Pa

2.2 改变m2对压强场的影响

通过数值模拟计算，得到m1和m3不变，即m1取0.4，m3取1.1，m2不同取值时消力池底板的时均压强，如图4所示。消力池上游段，水流刚进入消力池时，流速较大，水流动能较大，动能水头所形成的动水压强较大，时均压强较大，无论m2取何值，相对消力池其他位置，消力池上游段底板上时均压强均较大；水流进入消力池后，由于双层悬栅作用，水流与悬栅相互碰撞掺气消能，水流流速减小，水流动能减小，动能水头所产生的动水压强减小，时均压强减小，消力池上游段底板时均压强均较小。当m2改变时，消力池上游段底板时均压强存在一定差距，下游段底板时均压强变化不大，说明改变m2即改变栅距，对消力池下游段底板时均压强变化影响不大。

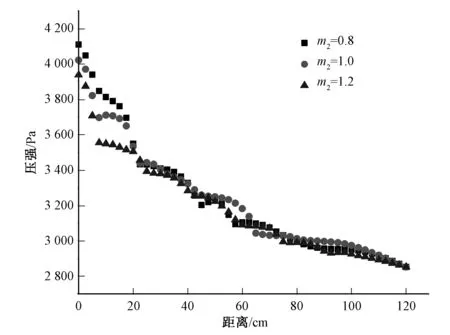
图4 m2不同取值时消力池底板时均压强Fig.4 The time average pressure of the bottom plate of the stilling basin in different value of m2

保持m1和m3不变，根据数值模拟计算，得到m2不同取值时消力池内各个悬栅时均压强差|Δp|，如表6所示。当m2取不同值时，消力池内第1根悬栅时均压强差均为最大；当m2取0.8时，最小时均压强差为1.85 Pa，在第12根悬栅处；当m2取1.0时，最小时均压强差为7.42 Pa，在第4根悬栅处；当m2取1.2时，最小时均压强差为5.06 Pa，在第12根悬栅处。

2.3 改变m3对压强场的影响

保持m1和m2不变，m1取0.4，m2取1.2，通过数值模拟计算，m3不同取值时消力池底板的时均压强，如图5所示。消力池上游段，水流刚进入消力池时，流速较大，水流动能较大，动能水头所形成的动水压强较大，时均压强较大，因此无论m3取何值，相对消力池其他位置，消力池上游段底板上时均压强均较大；水流进入消力池后，由于双层悬栅作用，水流与悬栅相互碰撞掺气消能，水流流速减小，水流动能减小，动能水头所产生的动水压强减小，时均压强减小，消力池上游段底板时均压强均较小。当m3取1.1时，消力池底板时均压强较小，由于消力池内水流流态相对其他布置型式稳定，水流波动较小，水流动水压强较小，说明该布置类型下，水流对消力池底板稳定影响较小。

表6 不同m2时各个悬栅时均压强差|Δp| Pa

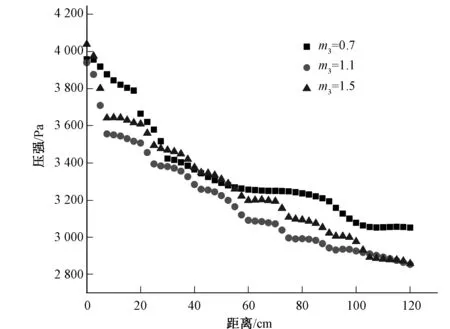
图5 m3不同取值时消力池底板时均压强Fig.5 The time average pressure of the bottom plate of the stilling basin in different value of m3

根据数值模拟计算，得到m1和m2不变，m3不同取值时消力池内各个悬栅时均压强差|Δp|，如表7所示。当m3取不同值时，消力池内第1根悬栅时均压强差均为最大；当m3取0.7时，最小时均压强差为9.03 Pa，在第4根悬栅处；当m3取1.1时，最小时均压强差为5.06 Pa，在第12根悬栅处；当m3取1.5时，最小时均压强差为2.93 Pa，在第6根悬栅处。

2.4 双层悬栅对压强影响变化

为更好地分析双层悬栅不同布置类型所受时均压强差的变化，定义悬栅所受时均压强差中大于100 Pa的时均压强差为高压差，记为P1；定义悬栅所受时均压强差中小于10 Pa的时均压强差为低压差，记为P2。通过计算得到双层悬栅不同布置类型的高压差与低压差出现的频率ξ(见表8、表9)：

(9)

式中：n表示悬栅根数；i取1、2；n1为高压差出现的悬栅根数；n2为低压差出现的悬栅根数；n总为总数(包括固定悬栅)。

由表8可知，m1取0.4时，高压差P1出现的频率ξ较大，为31.25%；m2取1.2时，高压差P1出现的频率ξ较大，为31.25%；m3取1.1时，高压差P1出现的频率ξ较大，为31.25%。

表7 不同m3时各个悬栅时均压强差|Δp| Pa

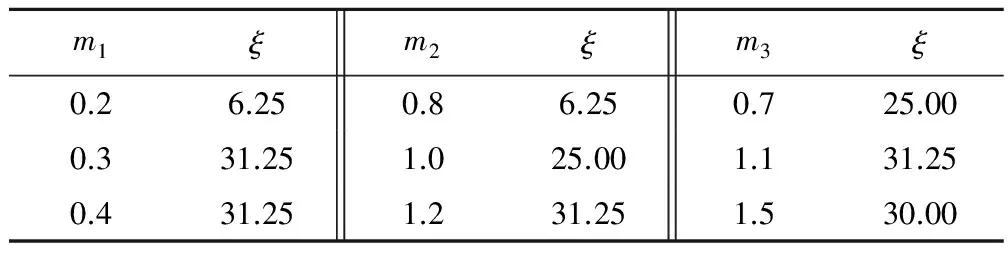
表8 悬栅不同布置类型高压差P1出现的频率 %

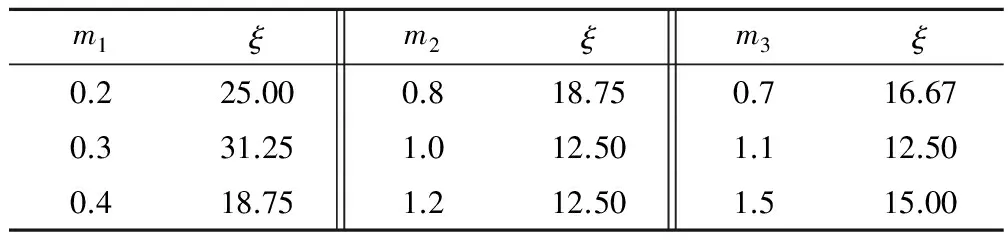
表9 悬栅不同布置类型低压差P2出现的频率 %

由表9可知，m1取0.4时，低压差P2出现的频率ξ较小，为18.75%；m2取1.2时，低压差P2出现的频率ξ较小，为12.50%；m3取1.1时，低压差P2出现的频率ξ较小，为12.50%。根据均匀正交试验得到消能效果较好的悬栅布置型式下，高压差出现的频率较大，低压差出现的频率较小，说明在双层悬栅较优布置型式下，水流与双层悬栅相互碰撞，充分掺气消能，水流对双层悬栅的作用较大，双层悬栅受水流冲击时间较长，双层悬栅结构稳定性影响较大，因此，在双层悬栅较优布置型式时，应提高悬栅的抗压强度。

3 结 语

通过数值模拟计算，得到以下结论。

(1)消力池内双层悬栅布置不同类型时，时均压强较大的部位主要分布在消力池上游段底板，压强差较大的部位主要分布在消力池上游段的悬栅，这些部位受水流冲击较大，存在安全隐患较大；双层悬栅不同布置类型，各个悬栅所受时均压强差均不一样，时均压强差分布差异较大。

(2)消力池内双层悬栅布置类型不同，各个悬栅上的高压差和低压差出现的频率均存在差异，在双层悬栅最优布置类型时，即m1=0.4、m2=1.2、m3=1.1时，悬栅所受高压差出现频率较大，低压差出现频率较小，存在安全隐患的部分较多。

□

[1] 蒋健楠，牧振伟，张佳祎. 消力池内双层悬栅对消能效果影响试验研究[J]. 水资源与水工程学报，2015，26(3)：157-160.

[2] 吴战营. 消力池内辅助消能工试验研究及数值模拟[D]. 乌鲁木齐：新疆农业大学，2013.

[3] 史志鹏，张广根，何婷婷. 低水头辅助消能工水力特性数值模拟计算研究[J]. 水电能源科学，2011，29(6)：106-108，123.

[4] 张宗孝，马 斌，魏文礼. 掺气分流墩墩头的动水压强特性研究[J]. 应用力学学报，2001，18(3)：54-59.

[5] 陆 杨，刘焕芳，金 瑾，等.T型墩间距对消力池效果影响的试验研究[J].水利水电技术，2013，44(11)：40-43.

[6] 李风兰，侯 杰，邱秀云，等.悬栅消力池消能特性的试验研究[J].新疆农业大学学报，2006，29(1)：63-66.

[7] 吴战营，牧振伟，潘光磊.导流洞出口消力池内设置悬栅消能工试验研究[J].水利与建筑工程学报，2011，9(4)：39-41，104.

[8] 朱玲玲，牧振伟，杨力行.悬栅消能工均匀正交设计及投影寻踪回归试验研究[J].水资源与水工程学报，2014，25(6)：210-214.

[9] 苏东朋，郝瑞霞. 齿墩式内消能工的水力特性数值模拟研究[J]. 水电能源科学，2015，33(11)：79-81，13.

[10] 李 华，郑铁刚，戴凌全，等. 多股多层水平淹没射流模型试验与数值模拟研究进展[J]. 水电能源科学，2010， 28(10)：74-76.

[11] 吴战营，牧振伟. 辅助消能工联合运用试验研究及数值模拟[J]. 中国农村水利水电，2013，(7)：111-117.

[12] 朱玲玲. 底流消力池内悬栅消能工布置型式对消能效果影响研究[D]. 乌鲁木齐：新疆农业大学，2014.

[13] 邱秀云. 水力学[M]. 乌鲁木齐：新疆电子出版社，2008.

[14] 蒋健楠，牧振伟，张佳祎，等 基于均匀正交设计的消力池内双层悬栅布置优化试验[J]. 中国水利水电科学研究院学报，2015，13(5)：357-362.

[15] Yakhot V，Orszag S A . Renormalization group analysis of turbulence I. Basic theory [J]. Journal of Scientific Computing, 1986, 1(1): 3 - 51.

[16] 王月华，包中进，王 斌. 基于Flow-3D软件的消力池三维水流数值模拟[J]. 武汉大学学报(工学版)，2012，45(4)：454-457，476.

[17] 尹进步，梁宗祥，郑 治，等. 与宽尾墩联合使用的消力池底板压强特性试验研究[J]. 水力发电学报，2011，30(4):103-108.