三峡水库中长期来水水量平衡模型研究

张 雅 琦

(中国长江电力股份有限公司三峡水利枢纽梯级调度通信中心，湖北 宜昌 443000)

1 水量平衡模型简介

水量平衡模型是一种以水量平衡原理为基础的概念性水文模型，它以降水、温度等气象因子作为输入，将各水文要素之间的关系概化成经验公式，并通过该经验公式来模拟流域水文过程。模型简单实用，广泛应用于流域中长期水文模拟、水资源供需分析以及大尺度气象模型输入数据的获取[1-3]。本研究采用熊立华等提出的2参数模型，结构简单，对资料要求不高，参数少，模拟精度令人满意。

(1)月蒸发量E。流域的年实际蒸发量采用下式计算：

E(t)=CEP(t) tanh [P(t)/EP(t)]

(1)

式中：E代表流域实际蒸发值；EP代表蒸发皿观测值；P代表降水量；C是模型的第1个参数(无量纲)。

(2)月径流量Q。月径流量Q与该月土壤中的净含水量S(扣除蒸发之后的剩余水量)有着十分密切的关系，S越大水分流出土壤的可能性越大，则Q越大。若把整个流域的调蓄作用视为一个“水库”，并将Q可以简化为S的双曲正切函数关系，即：

Q(t)=S(t) tanh [S(t)/SC]

(2)

式中：Q是月径流量；S是月土壤净含水量；SC定义为流域最大蓄水能力，mm，代表当土壤几乎没有水分时整个流域的平均持水能力。

(3)模型的数值计算方法 。已知月降水量P(t),月蒸发皿观测量EP(t)，则流域月实际蒸散发量E(t)，扣除蒸散发之后的土壤含水量为[S(t-1)+P(t)-E(t)]，其中S(t-1)为第(t-1)个月底，第t个月初的土壤含水量。然后计算流域月出流量Q(t)：

Q(t)=[S(t-1)+P(t)-E(t)]×

tanh{[S(t-1)+P(t)-E(t)]/SC}

(2)

最后得到第t个月底，第t+1个月初的土壤含水量S(t)：

S(t)=S(t-1)+P(t)-E(t)-Q(t)

(3)

2 2参数的确定及应用检验

2.1 资料收集整理

三峡水库平均入库流量用宜昌站(还原流量)平均流量代替；三峡水库以上采用长江上游面雨量资料；蒸发量资料不全，在计算过程中蒸发量数据均用历年各月均值数据代替。见表1。

2.2 模型的精度评定

模型的精度评定采用径流总量的相对误差和径流过程的确定性系数来评定。径流总量相对误差的绝对值越小，确定性系数越大，率定效果越好。

表1 历年气象要素及历年平均流量统计

(8)

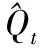
2.3 水量平衡型参数率定及检验

将三峡水库1951-2004年平均流量序列作为率定期，2005-2014年作为检验期。通过对参数调试后确定其月、汛、枯期以及年径流量模型参数，见表2。

表2 三峡水库径流量模型参数及模拟结果

表3为三峡入库月径流量误差检验结果，图1、图2为对比图。误差检验结果中多年年径流量平均误差为23.3%，历年年径流量最大平均误差32.7%，为2006年，其次是26.5%，为2013年；年径流量最小平均误差18.3%，为2012年，其次是18.5%，为2011年。分月看，6月份径流量平均误差最小，为10.8%，其次是3月份，为12.2%；12月份径流量平均误差最大，为46.9%，其次是11月份，径流量平均误差为40.2%。由于长江上游已建成的水库诸多，特别是枯期各水库开始蓄水，来水量受上游水库调蓄影响，入库流量计算值与实况值出入较大。

表4为三峡入库汛、枯期径流量检验结果与实况比较表，图3、图4为对比图。发现汛期径流量最大误差23.2%，为2012年，其次是11.9%，为2009年，汛期径流量最小误差-1.3%，为2005年，其次是-3.8%，为2007年；枯期径流量最大误差25.6%，为2008年，其次是20.9%，为2011年，枯期径流量最小误差-7.0%，为2009年，其次是7.4%，为2005年；2005-2014年10 a汛期径流量平均误差为9.7%，枯期径流量平均误差为12.7%，满足精度要求。

表5为三峡入库年径流量检验结果与实况比较情况，图5、图6为对比图。年径流量检验结果与实况比较发现，其径流量最大误差为26.7%，最小误差为零，平均误差为7.8%，满足精度要求。

表3 三峡入库月径流量误差检验结果 %

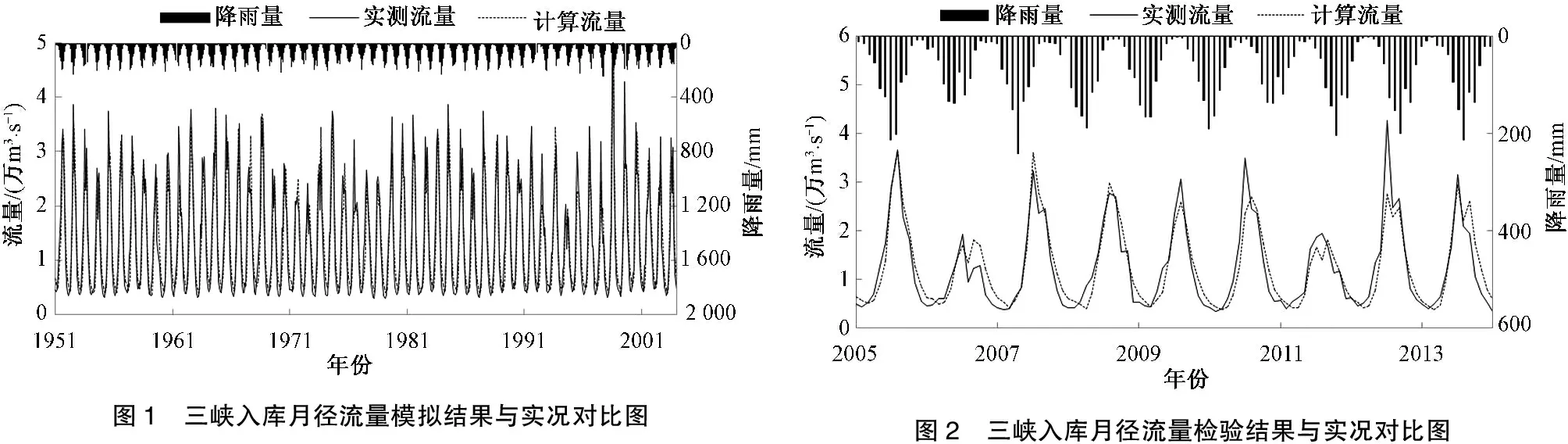
图1 三峡入库月径流量模拟结果与实况对比图图2 三峡入库月径流量检验结果与实况对比图

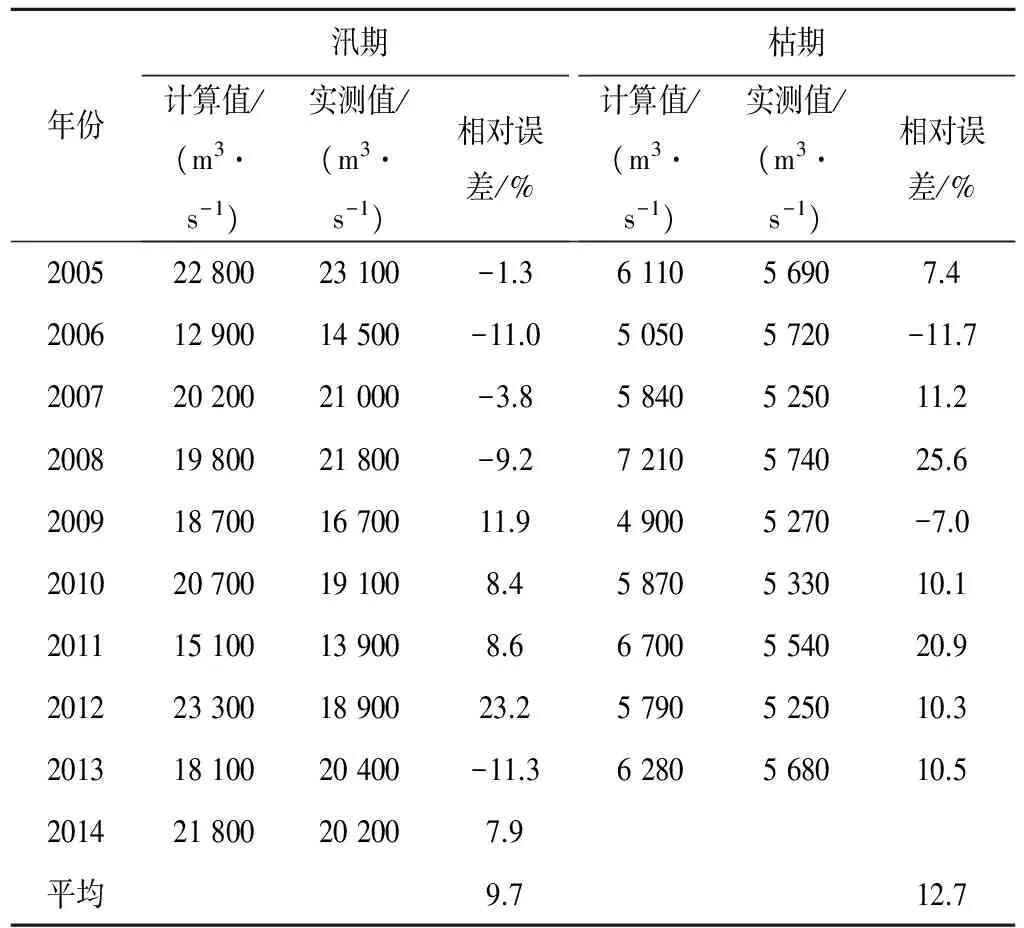
表4 入库汛、枯期径流量检验结果与实况比较

图3 三峡入库汛、枯期径流量模拟结果与实况对比

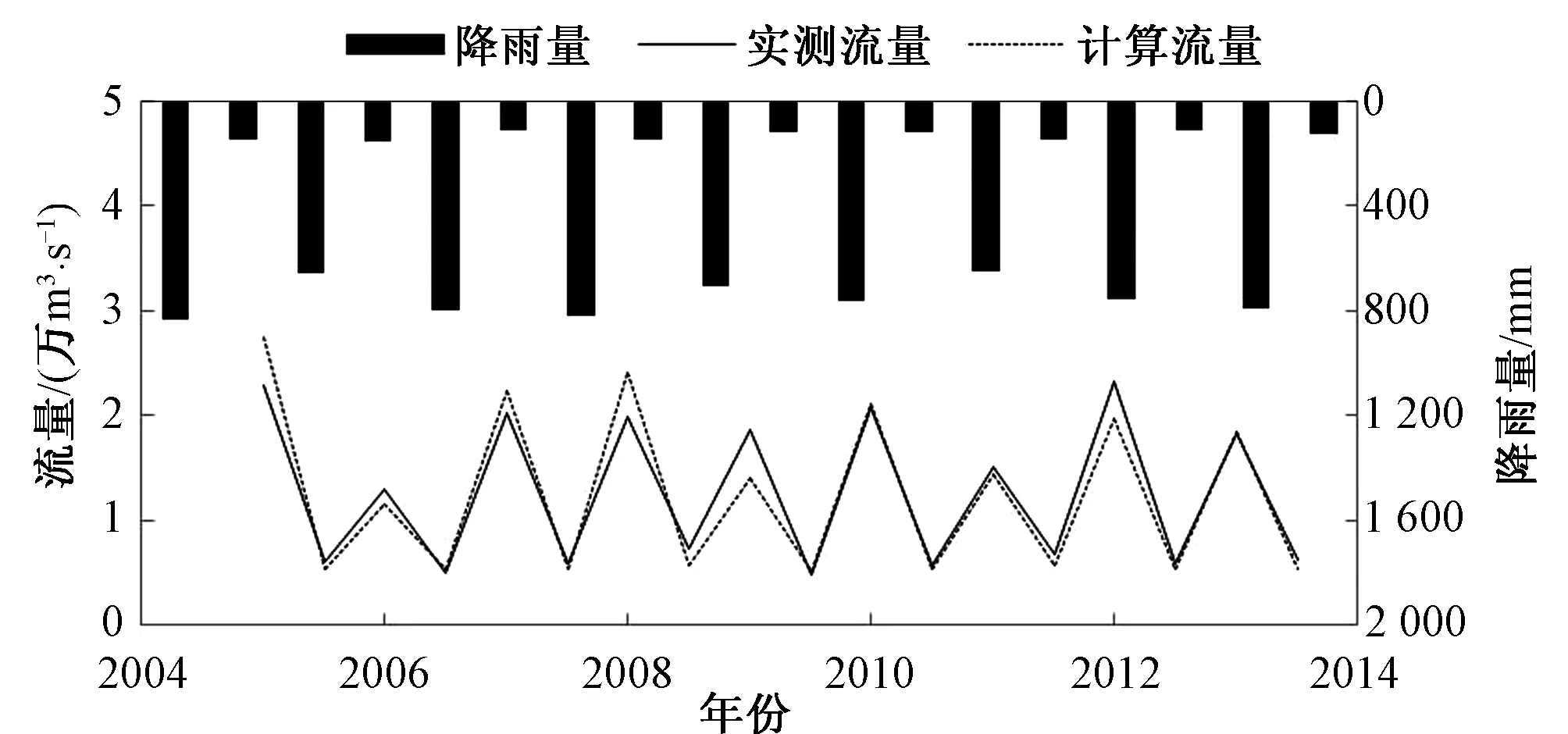
图4 三峡入库汛、枯期径流量检验结果与实况对比

3 水量平衡模型来水量模拟方案

研究采用简化了输入条件的2参数水量平衡模型来建立流域月、季(汛、枯)、年来水量模拟方案，具体步骤归纳如下：

(1)整理预报对象历年各月、季、年降水量，月、季、年蒸发量(用多年平均蒸发量代替)及历年各月、季、年径流量资料。

(2)根据所整理的资料，采用人工或优选方法优先模型参数C(蒸发值换算系数)和SC(流域最大蓄水能力)。

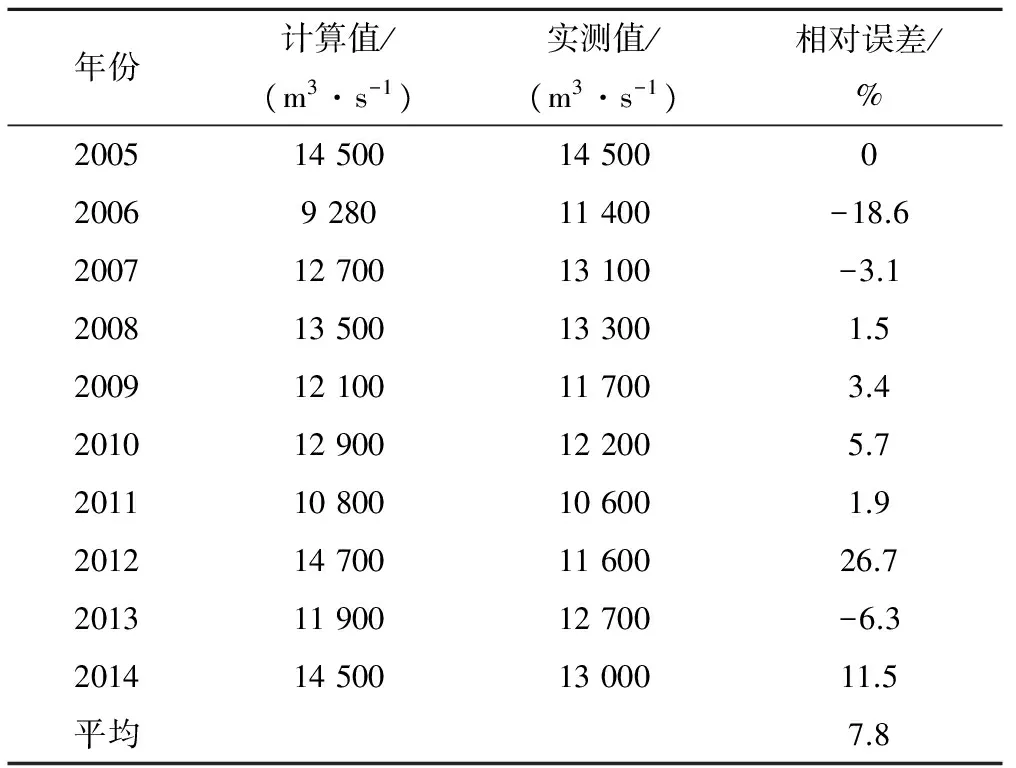
表5 三峡入库年径流量检验结果与实况比较

图5 三峡入库年径流量模拟结果与实况对比

图6 三峡入库年径流量检验结果与实况对比

根据步骤(1)～(2)，建立研究区域月、季、年水资源预测方案如下：

S(t)=S(t-1)+P(t)-E(t)-Q(t)

(9)

E(t)=CEP(t) tanh [P(t)/EP(t)]

(10)

Q(t)=[S(t-1)+P(t)-E(t)]×

tanh {S(t-1)+P(t)-E(t)/SC}

(11)

t=1,2,…,12

实际工作中，只需要获取研究区域下一月(或汛期、枯期和年)的降水量预估信息以及上游各水库计划蓄水量或泄水量，即可推算所求的来水量,实现对流域月(或汛期、枯季和年)径流量的模拟，见图7。

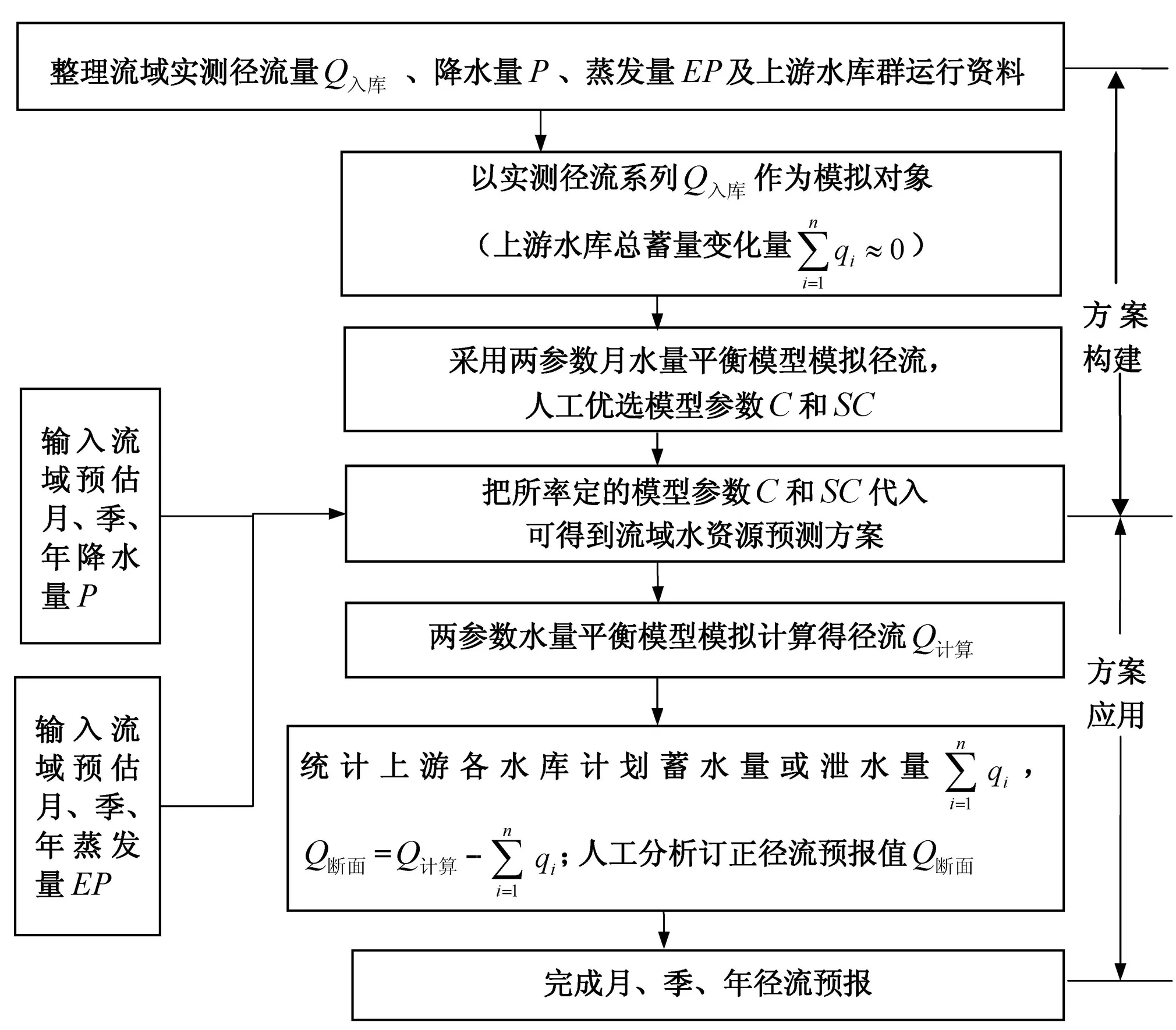
图7 来水量模型构造图

4 结 语

本文建立的2参数月水量平衡模型模拟精度较高，模型能较好地模拟月、季和年径流过程，模拟与实测的峰值对应关系也较好。在率定期和检验期，由于长江上游已建成的水库诸多，来水量受上游水库调蓄影响，入库流量计算值与实况值出入较大，三峡水库年平均流量其确定性系数Dc相对较低，分别为0.60和0.59，该数值较低，该模型模拟的年径流过程不好，不适用。其余均在0.86以上，确定系数最高的达0.97。径流总量相对误差值普遍较小，均控制在±5%以内，基本能够满足水量平衡。因此，2参数月和季水量平衡模型适用三峡水库。三峡水库年来水量计算值的平均误差5.8%(1951-2014年)，汛、枯期来水量计算值的平均误差为7.9%(1951-2014年)，月来水量计算值的平均误差为24.4%(1959-2014年)，基本满足精度要求。

□

[1] 熊立华,郭生练,付小华,等.两参数月水量平衡模型的研制和应用[J].水科学进展,1996,(7):80-86.

[2] 邓鹏鑫,胡庆芳,王银堂,等.GR模型与新安江模型及两参数月水量平衡模型在赣江流域的降雨径流模拟比较[J].河海大学学报,2014,42(5):382-387.

[3] 乐通潮,张万昌.双参数月水量平衡模型在汉江流域上游的应用[J].资源科学,2004,26(6):97-103.