基于三维固定裂缝模型的混凝土开裂数值模拟

王碗琴，强 晟，郭晓娜，周兰庭

(1.河海大学水利水电学院，南京 210098；2.南水北调中线干线工程建设管理局，北京 100038)

作为一种建筑材料[1-3]，混凝土因其取材广泛、价格低廉、抗压强度高等特性成为使用量最大、运用最广的材料。但是混凝土材料本身的弊端也逐渐暴露出来，其组织结构是一个多尺度多水平体系，内部含有大量形状、大小、位置都不同的微裂缝，在外荷载的作用下，微裂缝易扩展至宏观裂缝导致结构的破坏失稳。自1960年Kaplan[4]首次将断裂力学应用于混凝土开裂问题以来，混凝土断裂力学取得了很大进展。目前混凝土断裂模型主要可分为2大类[5]：①以双参数模型和双K模型为典型的等效弹性裂缝模型，此类模型忽略裂缝面上分布的黏聚力，将其等效为线弹性材料，用线弹性力学来判定裂缝发展，用P～CMOD,P～CTOD,P～δ曲线来表征混凝土的非线性特性；②以虚拟裂缝模型和裂缝带模型为典型的黏聚裂缝模型，此类模型便于数值分析，摒弃了传统力学认为裂缝尖端应力是无穷大的说法，考虑了裂缝面分布的黏聚力，主要是研究裂缝的形态和裂缝面非线性区域的软化特性。

虚拟裂缝模型由Hillerborg提出，考虑微裂面上的拉应力σ与裂缝张开度 之间的软化关系，但是随着裂缝面的扩展，需要重新划分网格。而Bazant和Oh[6,7]提出的裂缝带模型将断裂能弥散于裂缝带中，用应力～应变软化曲线σ=σ(ε)来描述裂缝面的软化关系，通过改变刚度矩阵来模拟开裂，不需要重新划分网格,通过调整应力～应变曲线来适应不同网格大小，以保证断裂能的唯一。但是断裂带模型的缺点[8]在于模型是用单元内平行密集的裂缝带来模拟裂缝，无法确定裂缝的宽度和位置。

根据对裂缝方向处理方法的不同，裂缝带模型又可以分为固定裂缝模型，多向固定裂缝模型和旋转裂缝模型。固定裂缝模型是假定裂缝方向固定，不随着裂缝扩展而变化，允许同一点产生多条裂缝，但同时也存在一定的缺陷[9,10]：一方面它没有考虑到主应力轴的旋转问题，会造成结果的突变；另一方面，没有考虑到与裂缝平行的混凝土会出现一定的弹性回弹，而认为裂缝附近的单元均超过抗拉强度，造成开裂单元数的误判。旋转裂缝模型的开裂方向则随着主应力轴或者主应变轴方向的变化而变化，但是在任意一点只允许产生一条裂缝。多向固定裂缝模型[11]则允许在一点形成任意条裂缝，且将裂缝角度限制在一定范围内，应用方面没有固定裂缝模型和旋转裂缝模型广泛。本文基于固定裂缝模型理论，编制Fortran程序来模拟混凝土开裂。

1 三维固定裂缝模型理论

1.1 本构关系

固定裂缝模型基于应变分解[12]思想，将材料应变分解成弹性和裂缝应变，即：

ε=εe+εcr

(1)

在开裂面建立局部坐标系n,s,t，局部坐标系与整体坐标系之间应力关系如下：

εcr=Necr

(2)

scr=NTσ

(3)

式中：σ、εcr分别为整体坐标系下单元应力和裂缝应变；scr、ecr分别为局部坐标系下裂缝应力和裂缝应变；N为坐标变换矩阵：

(4)

忽略裂缝面法向和切向应力与应变之间的相互影响[13]，定义局部坐标系下的应力和应变关系如下：

scr=Dcrsecantecr

(5)

(6)

式中：DⅠsecant、DⅡsecant分别表示Ⅰ型、Ⅱ型裂缝割线模量。

混凝土弹性本构关系为:

σ=Dεe

(7)

式中：D为弹性矩阵。

则综合式(1)、式(2)、式(3)、式(5)、式(7)可得三维混凝土开裂本构关系[14]：

σ=[D-DN(Dcrsecant+NTDN)-1NTD]ε

(8)

考虑到混凝土并不是完全的脆性断裂，而是存在一个软化过程，引入折减系数μ来体现混凝土从微裂到完全开裂这一过程的软化特性，引入剪切保留系数β来表示裂缝面的抗剪能力，一般取0.2。将混凝土和裂缝面的刚度视为串联关系[15],如图1所示。

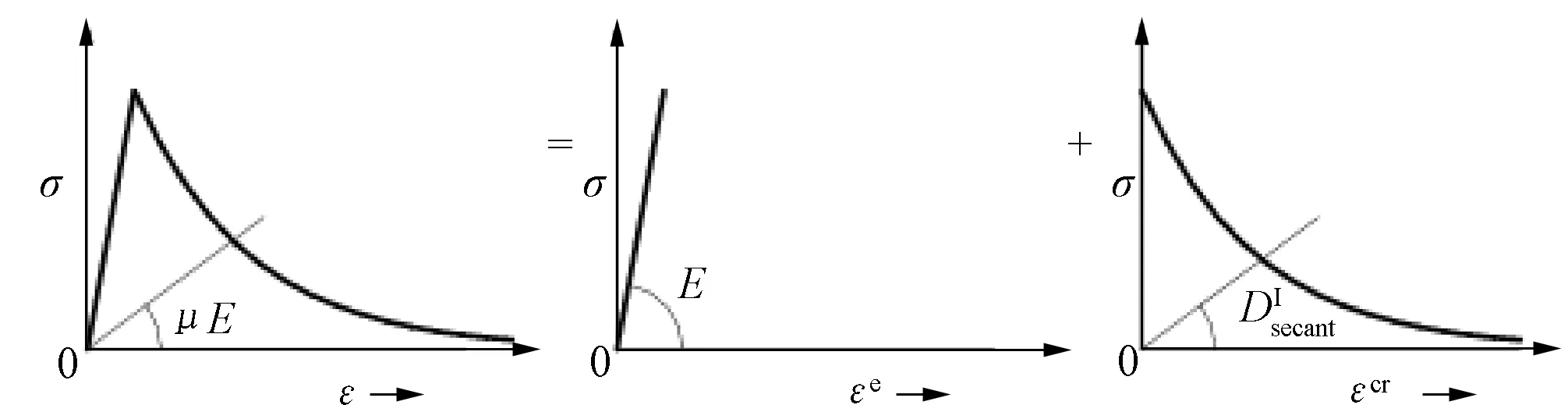
图1 混凝土与裂缝面刚度的串联关系Fig.1 The series relationship of concrete and fracture stiffness

可得：

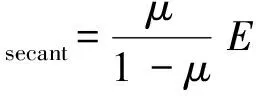
(9)

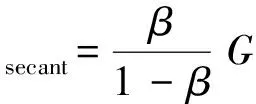
(10)

假定裂缝局部坐标系与整体坐标系重合，则n,s,t轴方向矢量分别为：

(11)

(12)

(13)

代入式(4)可得：

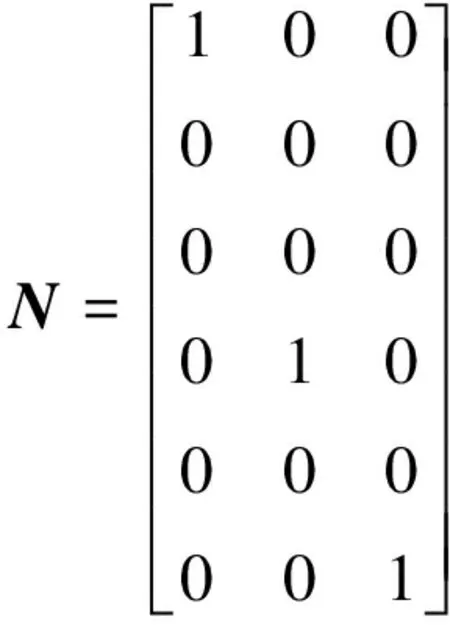
(14)

将式(9)、式(10)、式(14)代入式(8)计算可得裂缝局部坐标系与整体坐标系重合时混凝土开裂本构关系：

1.2 应力～应变曲线

应力～应变曲线是固定裂缝模型的一个重要参数，有线性、双线性、指数型等，其中线性应用最多，本文选取线性软化关系，如图2所示。

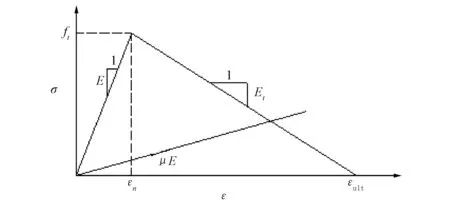
图2 应力～应变曲线Fig.2 The stress and strain curve

经推导可得折减系数的公式[16]如下：

(其中Et为负值)

(16)

式中：εult为极限拉应变；ε为整体坐标系下的全应变；如果ε>εult，则μ=0；如果ε<εn，则μ=1；否则μ则采用公式(16)计算。

1.3 断裂能Gf

断裂能是试件发生断裂外荷载所做的功，即试件断裂所释放的应变能。断裂能越大，则材料的延性越高，反之材料越脆。固定裂缝模型中，断裂能和应力～应变曲线有如下关系[15]：

Gf=Wareah

(17)

式中：Warea为应力～应变曲线所包围的面积；h为裂缝带宽度，即裂缝方向网格大小。

则线性软化关系中有：

(18)

传统弥散裂缝模型[17-20]，应变软化的结果对网格大小具有敏感性，如果带有应变软化特性的材料仅仅按照固定的应力～应变关系定义，或者说由固定的应力～应变关系确定，那么分散在断裂区的断裂能大小将随着单元加密而减小。而固定裂缝模型中，通过调整应力～应变曲线的下降段来保证断裂能的唯一。

2 算例验证

本文基于三维固定裂缝模型，编译Fortran程序，对3点弯曲梁断裂进行数值模拟，程序总体思路见图3。试件长2 m,宽0.2 m，高0.45 m。采用分步加载的形式，200个荷载步，每个荷载步大小为0.5 kN。混凝土弹性模量E=28.00 GPa,泊松比υ=0.2,剪切保留系数β=0.2，抗拉强度ft=2.5 MPa。选用3种不同网格尺寸，裂缝方向网格尺寸h分别为0.10，0.04，0.02 m。

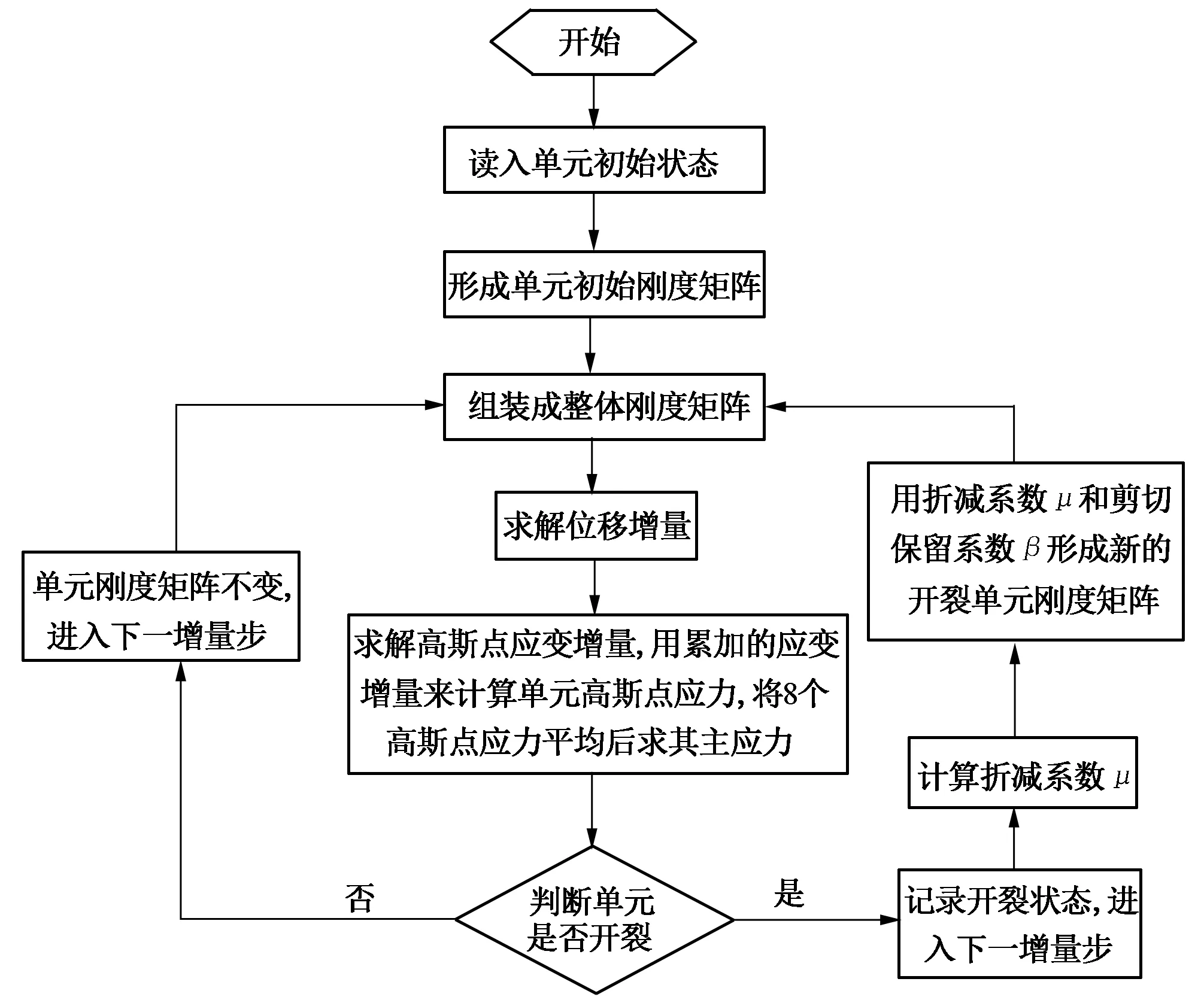
图3 程序计算流程图Fig.3 The flow chart of calculation

2.1 算例1

本算例验证断裂能的守恒准则。选用Gf=187.5 N/m，由式(18)可计算不同网格大小所对应的极限抗拉应变，3种网格参数具体见表1。

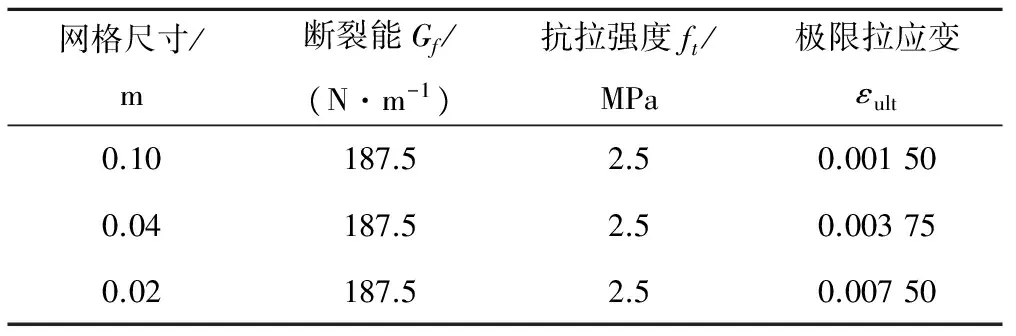
表1 不同网格参数Tab.1 The parameters of different grid models

选取特征点(1,0.1,0)进行计算，绘制特征点应力～应变曲线如图4～图6所示。

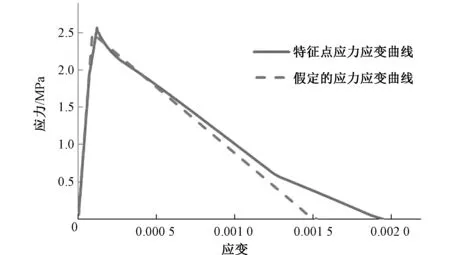
图4 h=0.10 m的特征点应力～应变曲线Fig.4 h=0.10 m the stress and strain curve of keypoint

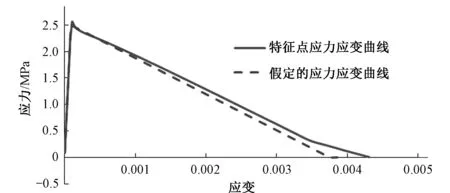
图5 h=0.04 m的特征点应力～应变曲线Fig.5 h=0.04 m the stress and strain curve of keypoint

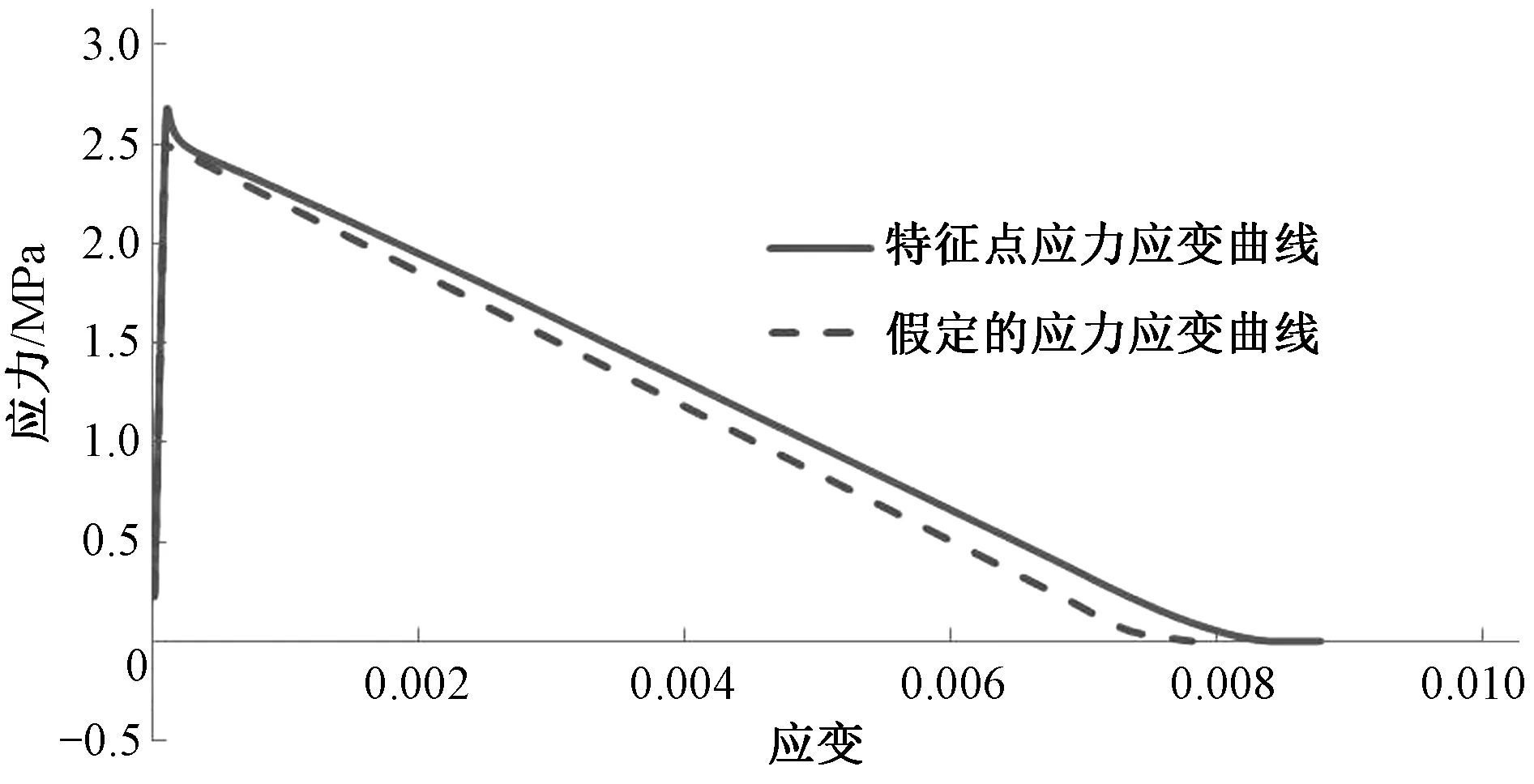
图6 h=0.02 m的特征点应力～应变曲线Fig.6 h=0.02 m the stress and strain curve of keypoint

从图4～图6可以看出：计算所得应力～应变曲线所围成的面积和假定应力～应变曲线所围成的面积误差很小，即计算所得断裂能基本符合预先设定的断裂能参数。所以固定裂缝模型中，根据网格大小来调整应力～应变曲线，可以保证断裂能的一致性，克服网格敏感性问题。由于该模型将断裂区之外的混凝土视为弹性材料，未考虑其非线性变形,且计算求解存在一定误差，所以计算所得下降段与假定的应力～应变曲线并不是完全吻合。

2.2 算例2

本算例选用不同断裂能对同一个网格尺寸模型进行计算，具体参数及结果见表2，其中极限荷载是指特征点达到极限拉应变εult时所对应的荷载大小。

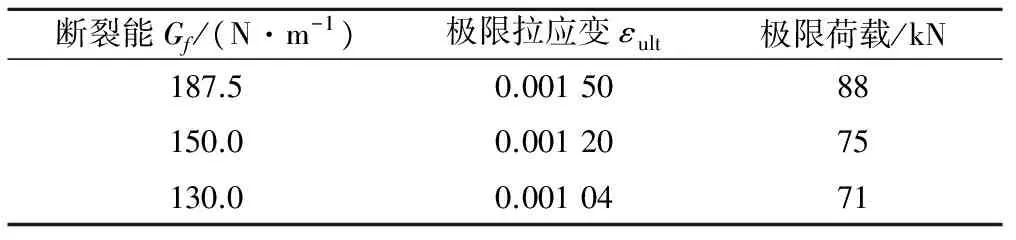
表2 计算参数Tab.2 The parameters of calculation

不同断裂能工况下特征点(1,0.1,0)的荷载-位移曲线和应变分布云图见图7～图11。

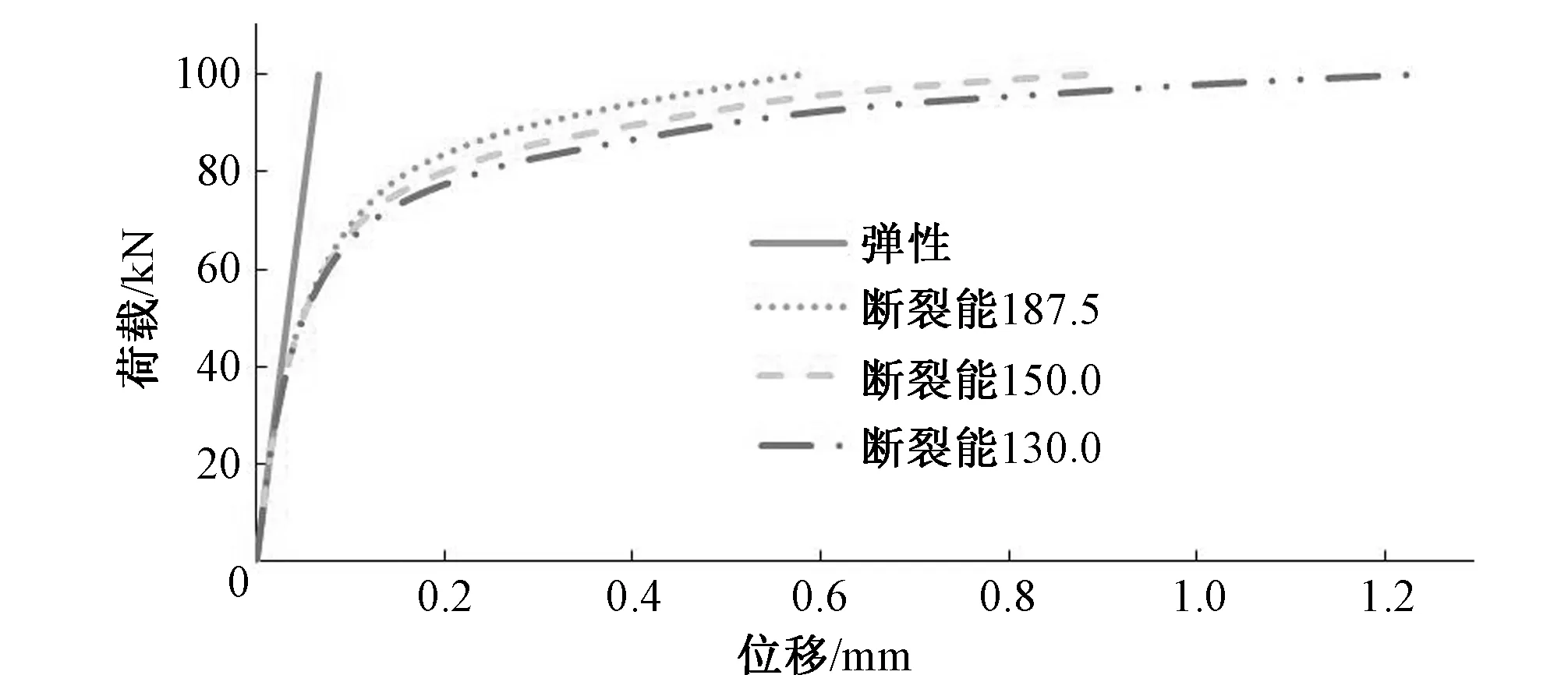
图7 不同断裂能下特征点的荷载～位移曲线Fig.7 The load displacement curves of keypoint with different fracture parameters

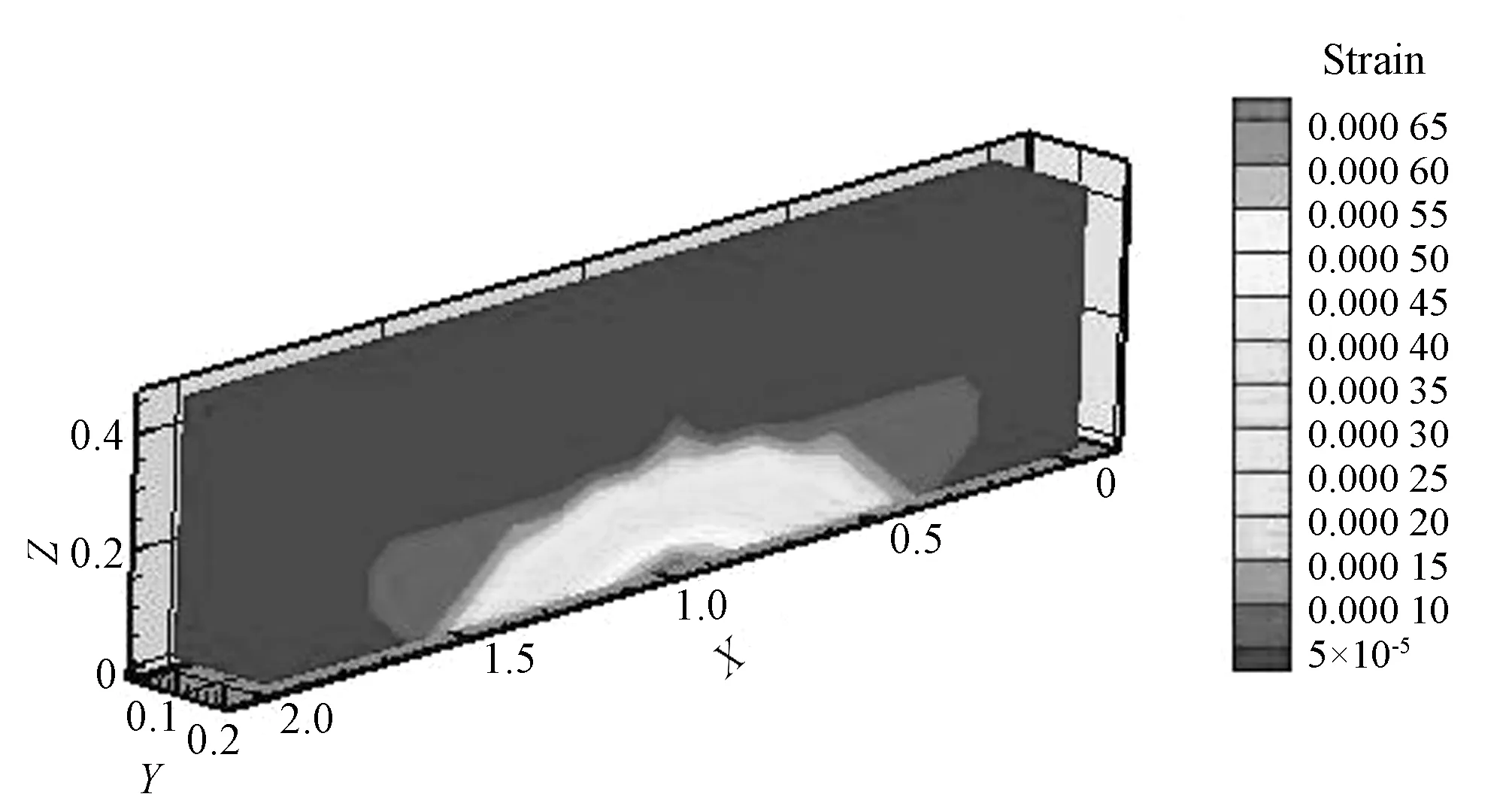
图8 不考虑开裂的应变包络图Fig.8 The strain envelope diagram regardless of crack

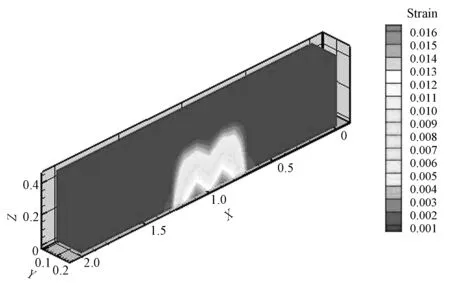
图9 Gf=130.0 N/m应变包络图Fig.9 Gf=130.0 N/m strain envelope diagram

图10 Gf=150.0 N/m应变包络图Fig.10 Gf=150.0 N/m strain envelope diagram

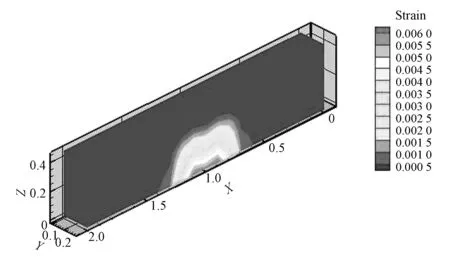
图11 Gf=187.5 N/m应变包络图Fig.11 Gf=187.5 N/m strain envelope diagram

由荷载～位移曲线图7和应变分布图8～图11可以看出，在相同荷载条件下，断裂能越小，节点位移、应变值越大，断裂能越大，节点位移、应变值越小。因此断裂能越小，试件断裂时外荷载所做的功越小，即材料越脆，在相同荷载条件下，越容易产生裂缝，而断裂能越大，即材料延性越好，试件承载力越大，符合实际情况。

3 结 语

本文基于三维固定裂缝理论，编制了相应的计算程序，通过2个算例验证了程序的正确性，并得到如下结论。

(1)固定裂缝模型根据网格大小调整应力～应变曲线，可以使计算结果不会因为网格的疏密而不同，克服网格敏感性问题。

(2)断裂能作为一种材料特性参数对混凝土结构性能的影响较大，断裂能越小，即混凝土材料脆性越大，可承载的荷载值就越小。

(3)混凝土弹性理论应力随着荷载线性增加，而固定裂缝模型作为一种非线性断裂力学模型，能够考虑断裂区的三维应力状态，考虑混凝土材料所具有的软化特性，即应力达到抗拉强度之后是会随着应变增加而逐渐减小，直至完全开裂，应力降为0，比较符合实际情况。

□

[1] Taliercio A L F, Gobbi E.Fatigue life and change in mechanical properties of plain concrete under triaxial deviatoric cyclic stress[J].Magazine of Concrete Research,1998,50(3):247-255.

[2] Yin W, Hsu Thomas T C.Fatigue behavior of steel fiber reinforced concrete in uniaxial and biaxial compression[J].ACI Materials Journal,

1995,92(1):71-81.

[3] 刘智光.混凝土破坏过程细观数值模拟与动态力学特性机理研究[D]. 大连：大连理工大学,2012.

[4] 蒋梅玲.基于断裂力学和损伤理论的混凝土断裂模型试验和数值研究[D]. 杭州：浙江大学,2010.

[5] 郭少华.混凝土破坏理论研究进展[J].力学进展,1993,(4):520-529.

[6] Bazant Z P. Crack band theory for fracture of concrete[J].Materials and Structures,1983,16(93):155-177.

[7] 李 翠.混凝土直接剪切试验的非线性有限元分析[D].大连：大连理工大学,2010.

[8] 张楚汉.论岩石、混凝土离散-接触-断裂分析[J].岩石力学与工程学报,2008,(2):217-235.

[9] 姜庆远,叶燕春,刘宗仁.弥散裂缝模型的应用探讨[J].土木工程学报,2008,(2):81-85.

[10] 韩 涛,安雪晖.钢筋混凝土三维多向固定裂缝本构模型[J].清华大学学报(自然科学版),2008,(6):947-950.

[11] 曲 蒙.早龄期混凝土损伤断裂的数值分析[D]. 杭州：浙江大学,2006.

[12] De Borst R,Nauta P. Non-orthogonal cracks in smeared finite element model[J].Engineering Computation,1985,2(3):35-46.

[13] 唐国斌,王统宁,项贻强.基于应变分解方法的钢筋混凝土开裂模型[J].工程力学,2013,30(3):174-180.

[14] 周元德,张楚汉,金 峰.混凝土开裂的三维非线性数值模拟[J].清华大学学报(自然科学版),2003,43(11):1 542-1 545.

[15] Rots J G, de Borst R. Analysis of mixed-mode fracture in concrete [J]. J of Eng Mech,1987,113(11):1 739-1 758.

[16] 徐世烺.混凝土断裂力学[M].北京:科学出版社,2011.

[17] Cervenka Jan，Bazant Zdenek P. Equivalent localization element for crack band approach to mesh-sensitivity in microplane model[J].International Journal for Numerical Methods in Engineering,2005,62(5):700-726.

[18] Rafi Muhammad Masood，Nadjai Ali.Comparison of numerical behaviors of FRP reinforced concrete beams using three smeared crack models[J].Materials and Structures/Materiaux et Constructions,2012,45(1-2):93-106.

[19] Mostofinejad D,Talaeitaba S B. Nonlinear modeling of RC beams subjected to torsion using the smeared crack model[J].Procedia Engineering,2011,14:1 447-1 454.

[20] Ozbolt Josko, Bazant Zdenek.Numerical smeared fracture analysis: nonlocal microcrack interaction approach[J].International Journal for Numerical Methods in Engineering,1996,39(4):635-661.