改进PSO-BP神经网络模型在海堤渗压监测中的应用

蓝祝光，黄 铭

(合肥工业大学 土木与水利工程学院，合肥 230009)

海堤作为沿海地区防御台风、抵御潮水的重要设施,其安全至关重要。绝大多数海堤使用时间长,并不断加固维修，导致其建造材料存在较大差别，且海堤常受到风浪潮、降雨等因素的影响，因此加重了堤身运行状态的复杂性[1-3]。加强海堤安全监测是保证海堤安全运行的重要手段，渗压作为海堤监测分析的主要项目，随着自动数据采集系统和网络技术的应用，海堤渗压信息的实时采集已能实现，如何对实测数据加以合理分析是当前研究的重点。

与库内水位相对稳定且变化平缓的土石坝不同，海堤面临的是受潮汐作用而发生快速变化且具有明显周期性的潮位[1,2]，而海堤渗压的变化规律与潮位变化密切相关。和变化相对平稳的土石坝渗压相比，海堤渗压具有变化快、周期复杂且明显的特点。

海堤渗压主要受到潮位、降雨、时效等因素的影响，渗压与各影响因素间的关系复杂，具有明显的非线性和不确定性[4]。传统BP神经网络具有很强的非线性映射能力、自学习能力和容错性等特点[5]，可以较好地模拟海堤渗压与各影响因素之间复杂的非线性关系；但基于梯度下降的BP神经网络存在收敛慢、难以脱离局部极小值等不足[6]。针对BP神经网络的不足，利用改进后的粒子群算法(PSO)快速的收敛特性和强大的全局搜索能力，将改进粒子群算法与BP神经网络结合起来。并根据海堤特点确定渗压的初选影响因子集，采用相关系数法分析各初选影响因子与渗压之间的相关性，筛选出与渗压关系密切的主要影响因子构建模型输入层，渗压作为模型输出层，形成海堤渗压改进PSO-BP监测模型，并利用该模型对海堤渗压进行预测研究。

1 粒子群算法(PSO)及其改进

粒子群算法(PSO)是基于群体智能的进化计算技术，最早是由美国的R.C.Kennedy和J.Eberhart教授受鸟群觅食行为的启发于1995年提出[7]。该算法可表述为在一个n维的搜索空间中，由m个粒子组成种群x=(x1,x2,…,xm)T，第i个粒子位置为xi=(xi,1,xi,2,…,xi,n)T，其速度为vi=(vi,1,vi,2,…,vi,n)T。每个粒子的位置xi代表问题在n维搜索空间的一个可能解，每个可能解对应一个适应值，依据适应值大小评价xi是否为最优解，粒子的适应值可通过将xi代入目标函数而求出。种群的个体极值为pi=(pi,1,pi,2,…,pi,n)T，全局极值为pg=(pg,1,pg,2,…,pg,n)T。通过搜寻以上两个极值，参照下式改变粒子的速度与位置：

(1)

(2)

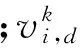
粒子群算法操作简单、收敛速度快、具有强大的全局搜索能力，可用于训练神经网络，通过全局搜索求解网络的连接权值。但该算法也存在以下问题：

(1)粒子群算法在接近或进入最优点区域时的收敛速度较为缓慢，缺乏有效机制逃离极小点。

(2)粒子都是依据全体粒子和自身的搜索经验来寻找最优解，可能会因为缺少对最优解的细致搜索而导致搜索精度不高。

为改善粒子群算法的不足、提高粒子群算法的探测和开发能力，通过引进惯性权重因子w值逐步递减的方法对粒子群算法进行改进[8]。较大的w值有助于逃离局部最优值，防止过早收敛；较小的w值有助于局部搜索，加快收敛速度[9]。改进后的粒子群算法为：

(3)

(4)

wk=-0.5(k/kmax)+0.9

(5)

式(5)中：k为迭代次数；kmax为最大迭代次数。

2 BP神经网络

BP神经网络是沿着误差函数减小最快的方向来改变网络的权值和阈值[10]。其学习分为两个阶段：①通过输入信号的正向传播，计算隐层和输出层的输出；②借助误差信号的反向传播对权值和阈值进行修正。算法步骤如下。

(1)随机初始化网络的所有权值和阈值。

(2)将tq、dq带入神经网络中，tq为输入值，dq为目标值，q为训练样本数。

(3)由前向后依次计算各层的输出。

隐层：

(6)

输出层：

(7)

式中：i为输入层节点数；j为隐层节点数；s为输出层节点数；os为模型实际输出值；uij为输入层到隐层的权值；cjs为隐层到输出层的权值；bj为隐层阈值；βs为输出层阈值。

(4)误差计算：

(8)

(5)误差信号从输出层向输入层反向传播，逐层修正各神经元的权值和阈值。

(6)将修改后的权值和阈值代回步骤(3)重新计算，直到q组样本训练结束，若达到误差精度要求或达到最大训练次数，则训练结束。

3 改进PSO-BP神经网络算法及实现

目前，BP神经网络在海堤渗压监测中已有所应用，但BP监测模型仍存在收敛速度慢、难以脱离局部极小值等不足。针对BP神经网络在海堤渗压监测应用中存在的不足，本文利用具有快速收敛特性和全局搜索能力的改进粒子群算法，取代BP神经网络的误差反向计算来求解网络模型的连接权值和阈值。

以m个n维向量的粒子构成粒子群体，每个粒子

x=(u11,u12,…,uij,c11,c12,…,cjs,

b1,…,bj,β1,…,βs)T

代表网络模型中所有的权值和阈值，粒子的初始值随机产生。而后依据BP神经网络的前向计算和整体平均误差求解每个粒子的适应值，粒子适应值计算公式为：

(9)

改进PSO-BP神经网络模型的建立步骤如下：

(1)确定网络拓扑结构，确定改进粒子群算法控制参数：粒子总数m、粒子初始位置xi,d和速度vi,d、最大训练次数kmax、加速常数c1和c2。

(2)根据输入、输出样本，以式(6)、(7)求解出模型的实际输出值，以式(9)求解出每个粒子的初始适应值，以当前粒子位置作为个体极值pi，选出最好的个体极值(即对应的适应值最小)作为全局极值pg，开始迭代。

(3)依据式(3)、(4)、(5)更新粒子速度和位置，依据公式(6)、(7)、(9)计算更新后粒子的适应值。如果第i个粒子更新后的适应值比更新前的小，则将更新后的粒子位置作为该粒子的个体极值pi；如果所有更新后的pi对应的最小适应值小于pg对应的适应值，则将该个体极值作为全局极值。

(4)根据更新后的个体极值和全局极值返回步骤(3)再计算，当训练达到最大次数或满足最小误差要求时，训练结束，pg的位置即为神经网络模型的连接权值和阈值。

(5)模型依据最终的权值和阈值进行预测。

4 海堤渗压改进PSO-BP监测模型的建立与应用

以浦东某处海堤作为研究对象，根据实测资料建立海堤渗压改进PSO-BP监测模型。确定监测模型的输入层、输出层及相应神经元数是建模的重点之一。

已有研究表明[11]，对海堤渗压影响最明显的是潮位的变化，由实测资料分析可知，渗压的变化相对潮位来说具有滞后性。为使选取的潮位因子更为合理，取ε时段前的潮位HP,ε形成监测模型的基本潮位因子形式。通过计算序列马氏距离D进行比较来确定HP,ε：

(10)

式中：E、F为要计算的序列，分别对应前期潮位序列与待分析的渗压序列；V为协方差阵，由样本估计得到。

海堤一般为土石结构且位于暴雨频发的区域，渗压极易受到降雨影响，应将降雨作为渗压的影响因素予以考虑。因受到土体等堤坝材料的影响作用，降雨引发的渗透对渗压的影响具有一定的滞后性，在类似的水工建筑物监测模型中，通常采用前期降雨量总和或平均降雨量作为降雨因子，本文采用前一天的降雨量总和R1、前两天的降雨量总和R2作为初选降雨因子。

因海堤是长期运行的土石建筑物，建模时应考虑时效作用的影响。目前，时效作用对海堤的影响机理研究尚浅，可参考大坝监测模型的建模经验，以时间函数作为时效因子参与模型建立。本文采用T、T2、T3作为模型的初选时效因子。

因初选因子数量较多、可参与建模的因子组合方式多种多样，为筛选出渗压的主要影响因子参与模型建立、提高模型的训练速度和预测精度，采用相关系数法分析各初选影响因子与海堤渗压的相关性，从中筛选出主要影响因子参与构建模型。相关系数r的计算公式为[12]：

(11)

|r|越大，各影响因子与渗压的相关性越大；反之则越小。根据式(11)，计算算例各初选影响因子与海堤渗压的相关系数，计算结果如表1所示。

表1 初选影响因子与海堤渗压的相关系数表Tab.1 Correlation coefficients of primary impact factors and seawalls seepage pressure

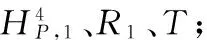
(12)

式中：h为样本数；dλ为目标值；oλ为模型实际输出值。

模型训练的整体平均相对误差为0.442%，训练结果如图1所示。由图可见，海堤渗压变化迅速、具有明显周期性，该模型能很好地反映渗压的主要规律和整体变化趋势，训练效果良好。

图1 海堤渗压改进PSO-BP监测模型训练结果Fig.1 Training results of seawall seepage pressure modified PSO-BP monitor model

将训练后的改进PSO-BP监测模型对后期48 h的渗压值进行预测，并与后期实测值比较分析，预测结果见图2。结果显示预测整体平均相对误差为0.402%，最大相对误差为1.091%，预测值与实测值趋势吻合，精度高。对于变化迅速的海堤渗压而言，监测模型能对后续48个渗压值的大小及趋势获得如此高精度的预测效果，证明本文建立的改进PSO-BP模型性能优越，效果稳定。

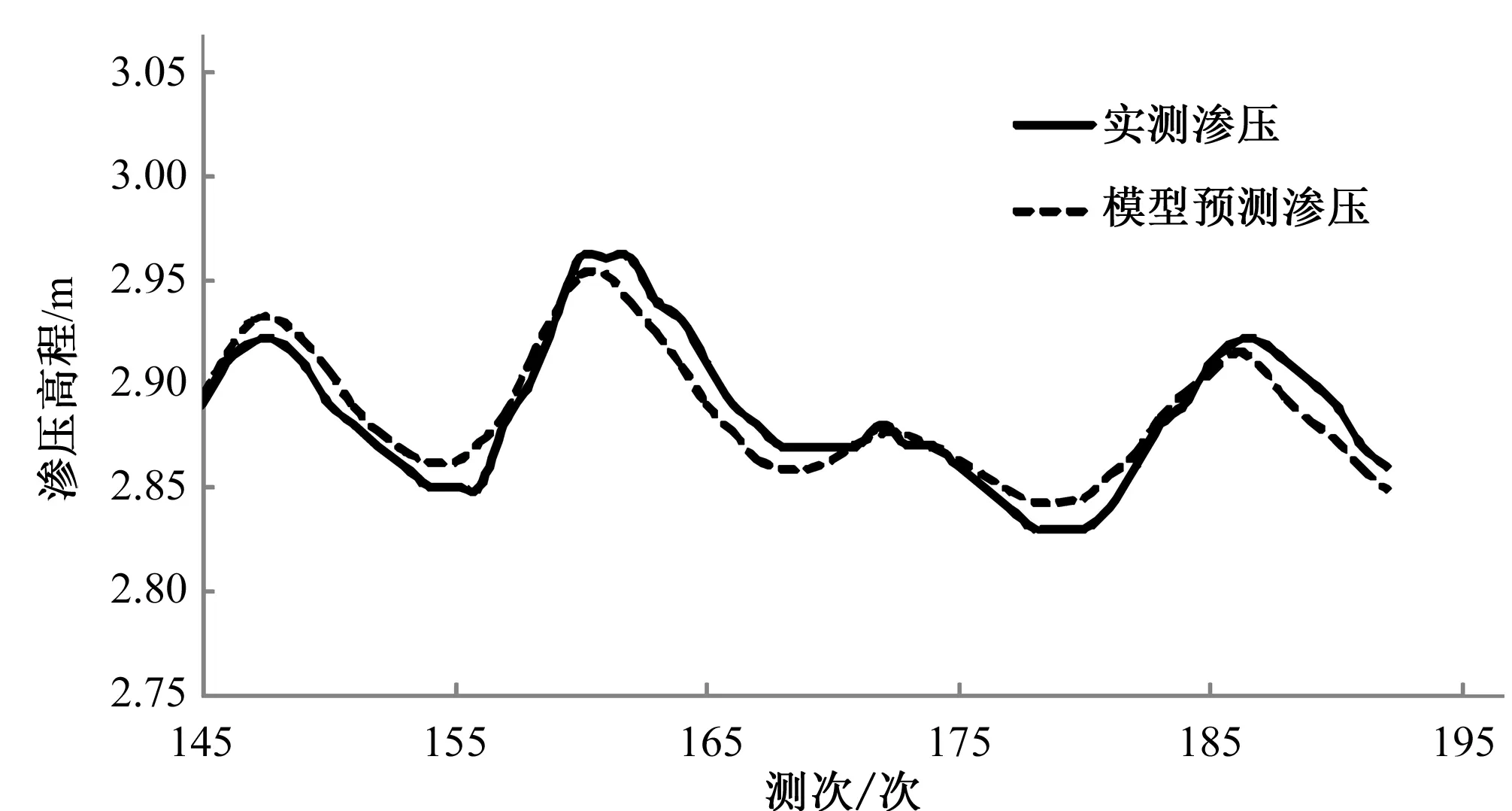
图2 海堤渗压改进PSO-BP监测模型预测结果Fig.2 Predicted results of seawall seepage pressure modified PSO-BP monitor model

为显示海堤渗压改进PSO-BP监测模型的优越性，以传统BP神经网络对上述算例信息进行建模以作比较。从表2两种模型训练情况可看出，改进PSO-BP监测模型的训练效果明显优于BP监测模型。

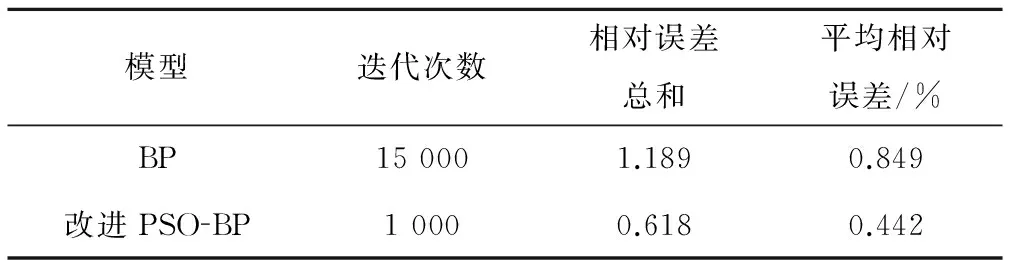
表2 BP、改进PSO-BP模型训练性能对比表Tab.2 Training performance comparison of BP model and modified PSO-BP model

对两种模型的预测结果进行对比分析，BP监测模型预测的平均相对误差为0.676%、最大相对误差为1.606%，相比之下，改进PSO-BP监测模型的预测精度也高于BP监测模型。

5 结 语

根据海堤特点及实测信息，分析确定渗压的初选影响因子集，采用相关系数法筛选出主要影响因子，以此构建模型输入层，以对应渗压作为模型输出层，利用改进粒子群算法对传统BP神经网络的连接权值和阈值进行全局优化搜索，建立海堤渗压改进PSO-BP监测模型。计算结果表明，改进PSO-BP模型较大地提高了收敛速度和精度，克服了BP神经网络在海堤渗压监测应用中收敛速度慢的不足，具有更高的预测精度和更强的预测能力，对后续的海堤渗压监测研究起到借鉴作用。

□

[1] 黄 铭.数学模型与工程安全监测[M].上海：上海交通大学出版社，2008.

[2] 黄 铭，刘 俊.海堤渗压周期特征分析及其在神经网络监测模型中的应用[J].应用基础与工程科学学报，2010,18(2)：330-335.

[3] 陆迎寿，黄 铭，蓝祝光. 人工神经网络在海堤非稳定渗流参数反演中的应用[J].南水北调与水利科技，2015,13(6)：1 147-1 150.

[4] 黄 铭，刘 俊.海堤渗压多测点径向基函数监测模型的建立[J].上海交通大学学报，2012,46(10)：1 675-1 679.

[5] 周 喻，吴顺川，焦建津，等.基于BP神经网络的岩土体细胞观力学参数研究[J].岩土力学，2011,32(12)：3 821-3 826.

[6] 罗 丹，李昌彩，吴长彬.基于微粒群-BP神经网络算法的堆石坝坝体变形监控模型研究[J].岩石力学与工程学报，2012,31(1)：2 926-2 931.

[7] 常晓林，喻胜春，马 刚，等.基于粒子迁徙的粒子群优化算法及其在岩土工程中的应用[J].岩土力学，2011,32 (4)：1 077-1 082.

[8] Shi Y, Eberhart R. Empirical study of particle swarm optimization. Proceedings of the 1999 Congress on Evolutionary Computation, 1999:1 945-1 950.

[9] Shi Y, Eberhart R C. A modified particle swarm optimizer. Proceedings of the IEEE Conference on Evolutionary Computation,1998:69-73.

[10] 周 娟，黄 铭.基于改进BP神经网络的海堤渗压监测模型研究[J].人民长江，2014,45(3)：90-93.

[11] 黄 铭，刘 俊.海堤渗压监测因果模型基本结构和因子选择[J].上海交通大学学报，2008,42(11)：1 931-1 934.

[12] 陈西江，鲁铁定，谭成芳.大坝位移BP网络模型影响因子的优选[J].江西科学，2010，28(1)：72-76.

[13] 王德明，王 莉，张广明.基于遗传BP神经网络的短期风速预测模型[J]. 浙江大学学报(工学版)，2012,46(5)：837-841.

[14] 田雨波.混合神经网络技术[M].北京：科学出版社，2009.

[15] 王晓萍，孙继洋，金 鑫.基于BP神经网络的钱塘江水质指标的预测[J]. 浙江大学学报(工学版)，2007,41(2)：361-364.