基于格子玻尔兹曼的管道重力流充水和排空三维瞬变过程模拟

孟兆芳，蒋 劲，李燕辉，符向前

(1. 甘肃省水利厅水利管理局, 兰州 730000; 2. 武汉大学动力与机械学院, 武汉 430072)

0 引 言

常见的压力管道输水有泵流和重力流两种输送方式。泵流输水系统主要包括泵站、输水管道和其他水工建筑物等，以水泵作为系统能量源，将用水输送到远方。而重力流系统则完全依赖水流的落差重力作用，不需要水泵加压，将水从水源地输送到远方用水户。重力流输水方式最大限度利用了水流的落差势能，运行成本低，经济性好，是理想的输水方式[1]。随着经济建设的快速发展，工业和人们生活用水量迅速提高，各地大中型重力流管道输水工程也越来越多。保证重力流管道安全运行是一道工程难题，包括流量控制、水锤压力防护和进排气等众多问题[2]。重力流的常见研究方法是利用一维系统分析软件进行数值模拟，但当管径较大时，径向流场变化明显，将管道空间简化为一维的管轴线会使模拟结果失真。另外，一维仿真对系统内的泵阀启闭过程和管道转折处等特殊部位的瞬态流场分析也不适用。

格子玻尔兹曼方法是一种新兴的流体数值计算方法，其形式简单，计算局部性强，能灵活处理复杂的边界问题，且完全并行，非常适合在大规模计算机群上运行[3]。目前该方法已在国内外被广泛应用于流动和传热领域的研究，包括：对湍流、多相流等基础流体力学问题进行深入研究[4-6]；对室内通风换热、房屋外风压和地下巷道热流分布等建筑物流场进行分析[7-9]；对弯道水流、鼓泡床离散颗粒和间隙渗流等具体工程问题进行模拟[10-12]；对流动与传热过程进行微尺度的探讨等[13,14]。

本文利用基于格子玻尔兹曼方法的新型无网格CFD方法分析三维重力流管道系统的充水和排空过程，以新的数值计算方法分析系统级别的流场瞬变过程是一个创新的研究方向。为节约计算资源和时间，仅取长度较短的小型管道系统作为研究对象，着重从原理上说明计算的可行性。

1 数学模型

1.1 重力流数学模型

图1为常见的重力流系统[15]，液体从V-1截面流至V-2截面。其中，V-1处的压力和温度分别为P0(Pa)和T0(K)，管道入口处为P1和T1，V-2(管道出口水平面)处为P2和T2。以地面为基准，三处高度分别是H0(m)、H1和H2。液体在高差的驱动下由V-1流向V-2。为方便分析，对系统做出一些假定：管径无变化，液体密度恒定，流动过程无闪蒸等复杂现象，同时系统不涉及传热过程，即T0、T1和T2相等。

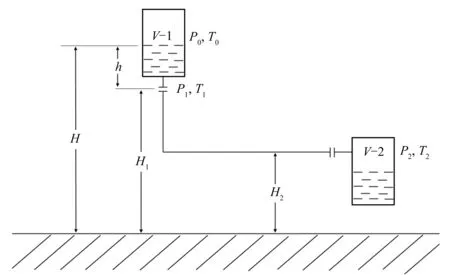
图1 常见重力流系统Fig.1 Common system of gravity flow

在重力流流动过程中，整个系统机械能守恒，有：

(1)

式中：m1和m2分别是进口和出口质量流量，kg/s；u1和u2分别是进口和出口流速，m/s；ρ是液体密度，kg/m3；E为系统能量损失，J。

当管流为满管流时，由于管径和密度不变，则进、出口质量流量相同，流速相同，即：

m1=m2=m

(2)

u1=u2=u

(3)

此时，系统的能量损失包括入口损失、管道损失和出口损失，E的表达式为：

(4)

式中：k1和k2分别是管道进口和出口的阻力系数；D是管道直径，m；Li是不包括进出口的分段管道当量长度，m；λi是分段管道沿阻系数；ζj是局阻系数。

以水头形式表示重力流的总推动力为：

X=(H1-H2)+(P1-P2)/ρg

(5)

1.2 格子玻尔兹曼方法

在物理学中对流体流动描述有三个层次：宏观、微观和介观[16]。基于介观模型的格子玻尔兹曼方法以流体的分子运动论为基础，根据微观运动过程的基本特征建立了简化的时间和空间完全离散的动力学格子模型[17]：在格子之间分布的众多介观流体粒子根据一定的法则沿格线迁移并在格点上发生碰撞，运动过程遵从动力学定律并服从统计定律，通过对流场中大量粒子的统计平均得出流体的宏观运动变量。

格子玻尔兹曼方法与传统CFD的N-S方程算法相比，最大的特点就是求解的无网格化，只需定义格子尺寸即可。另外其还有许多独特的优点：①从微观粒子角度进行模拟，可以比较方便地处理不同组分、不同流体间界面间的复杂相互作用不需要借助经验和半经验公式；②相对于N-S方程的非线性对流项，格子玻尔兹曼方法相空间对流过程是线性的，求解更容易，演化过程更清晰；③压力用状态方程表示，不必与速度迭代求解，算法比较简单。

采用单松弛时间算子[18]且带体积力项的格子玻尔兹曼方程如下：

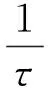
(6)

上式通常分解为碰撞步和迁移步两种演化形式[19]：

碰撞步：

(7)

迁移步：

(8)

而局部平衡态分布函数为：

(9)

作为计算流体力学中一种高效的介观数值方法，利用格子玻尔兹曼方法模拟三维重力流能得到较高的计算精度。

2 计算方案及结果

2.1 重力流管道充水

图2是管道重力流充水计算模型，其中高位水池液位高差是50 m，管道高差60 m，管径1 m。在管道进口处设置一闸阀，充水时设置闸阀在60 s内线性开启，总仿真时间为110 s。

图2 重力流管道充水计算模型Fig.2 Computing model of filling gravity flowed pipes

重力流管道充水过程的管内液面变化如图3所示，其中管道充满水的时间为95 s。

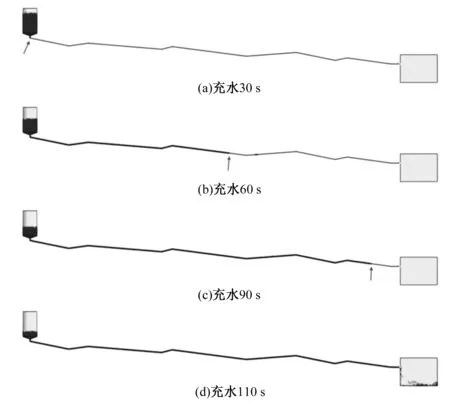
图3 充水过程液面位置变化情况Fig.3 The changing liquid level in filling process

管道进口闸阀开启过程的管内流速变化如图4所示。

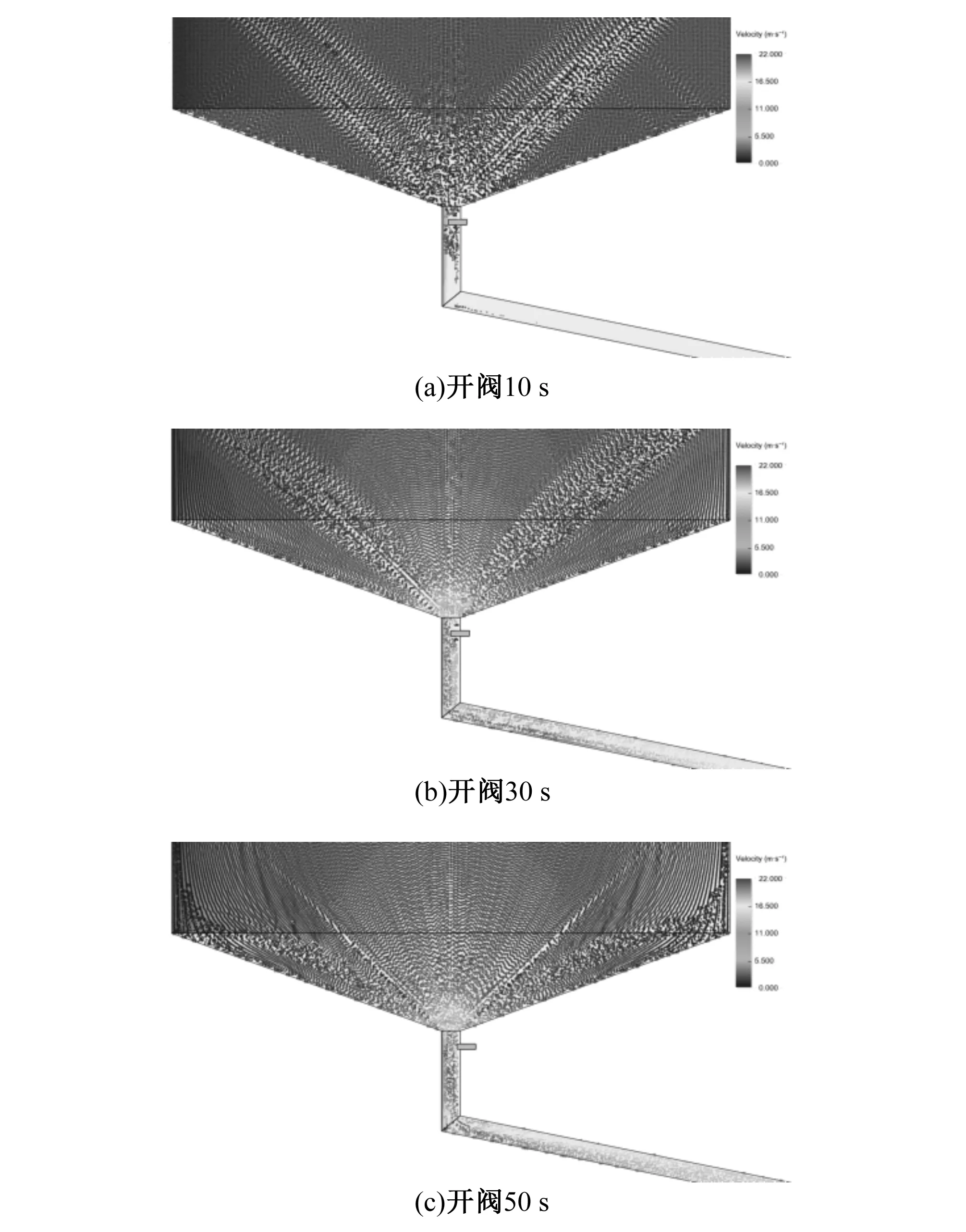
图4 开阀充水过程管内速度场变化情况Fig.4 The changing velocity distribution with the opening gate valve in filling process

取位于进口闸阀后面1m处管轴线上的一点作为监测点，提取重力流管道充水过程中该点的压力和流速值，变化曲线分别如图5和6所示。

图5 充水过程监测点压力变化Fig.5 The changing pressure of monitoring point in filling process

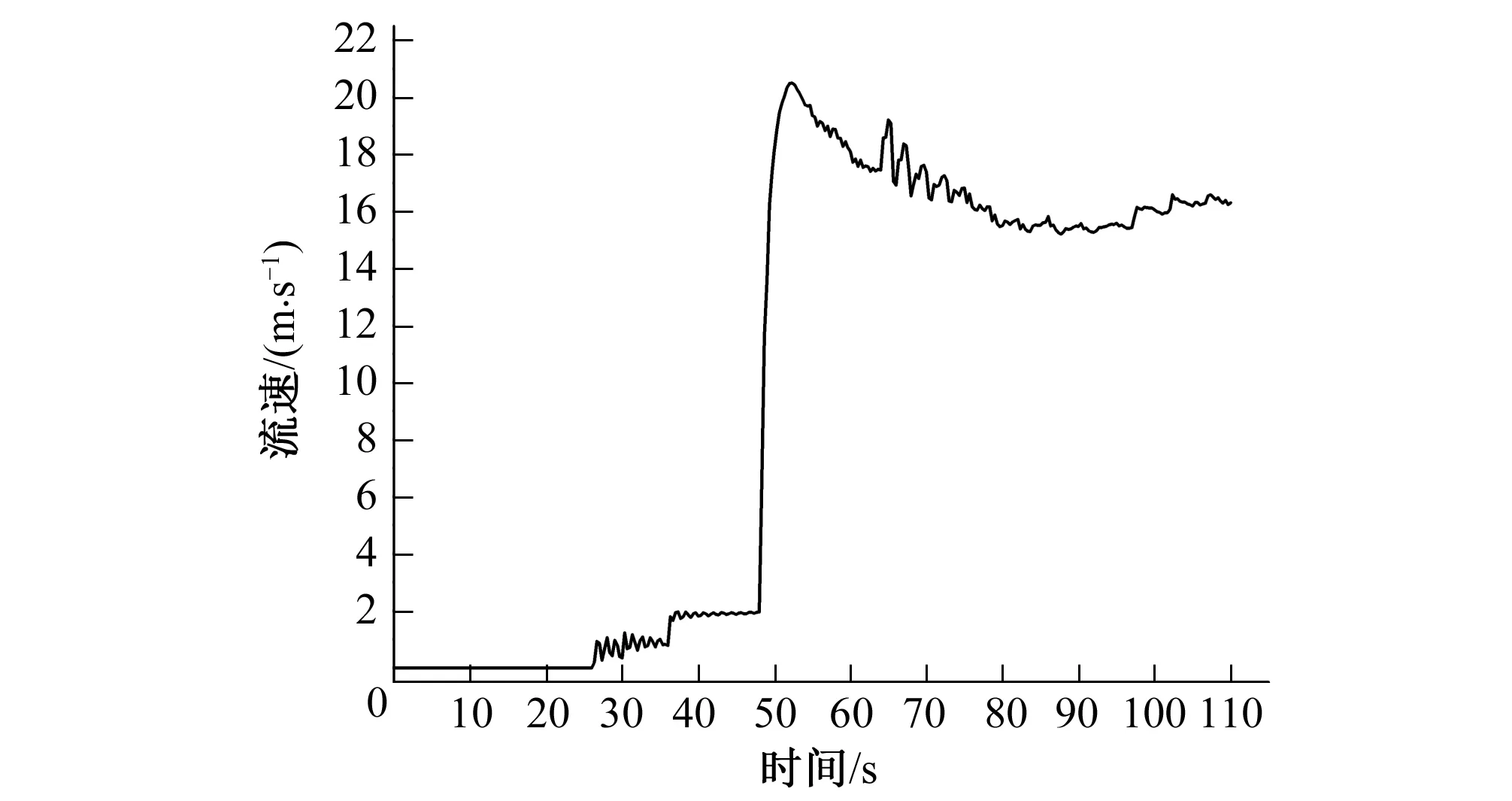
图6 充水过程监测点流速变化Fig.6 The changing velocity of monitoring point in filling process

监测点位于阀后轴线上，受开阀产生的紊流影响，该点处的流速和压力有较大波动。阀门开度较小时，水流主要沿管壁流动，监测点上的压力和流速变化较小。而闸阀开启50s左右时，压力和流速均有一快速上升过程，随后压力持续下降，而流速则维持比较稳定的状态。

2.2 重力流管道排空

图7是重力流管道排空计算模型，初始时刻管道充满水，液位高差60 m，管径1 m。在管道出口处设置一闸阀，排空时设置闸阀在60 s内线性开启，总仿真时间为100 s。

图7 重力流管道排空计算模型Fig.7 Computing model of draining gravity flowed pipes

重力流管道排空过程的管内液面变化如图8所示，管道完全排空的时间为89 s。

图8 排空过程液面位置变化情况Fig.8 The changing liquid level in draining process

管道出口闸阀开启过程的流速变化如图9所示。

在将超高速动能武器打击效应等效成浅埋爆炸后，可根据岩石中浅埋爆炸效应，计算出超高速动能武器打击时，地冲击应力波形参数。目前计算岩石中爆炸的应力波参数常用的计算公式为[17-18]

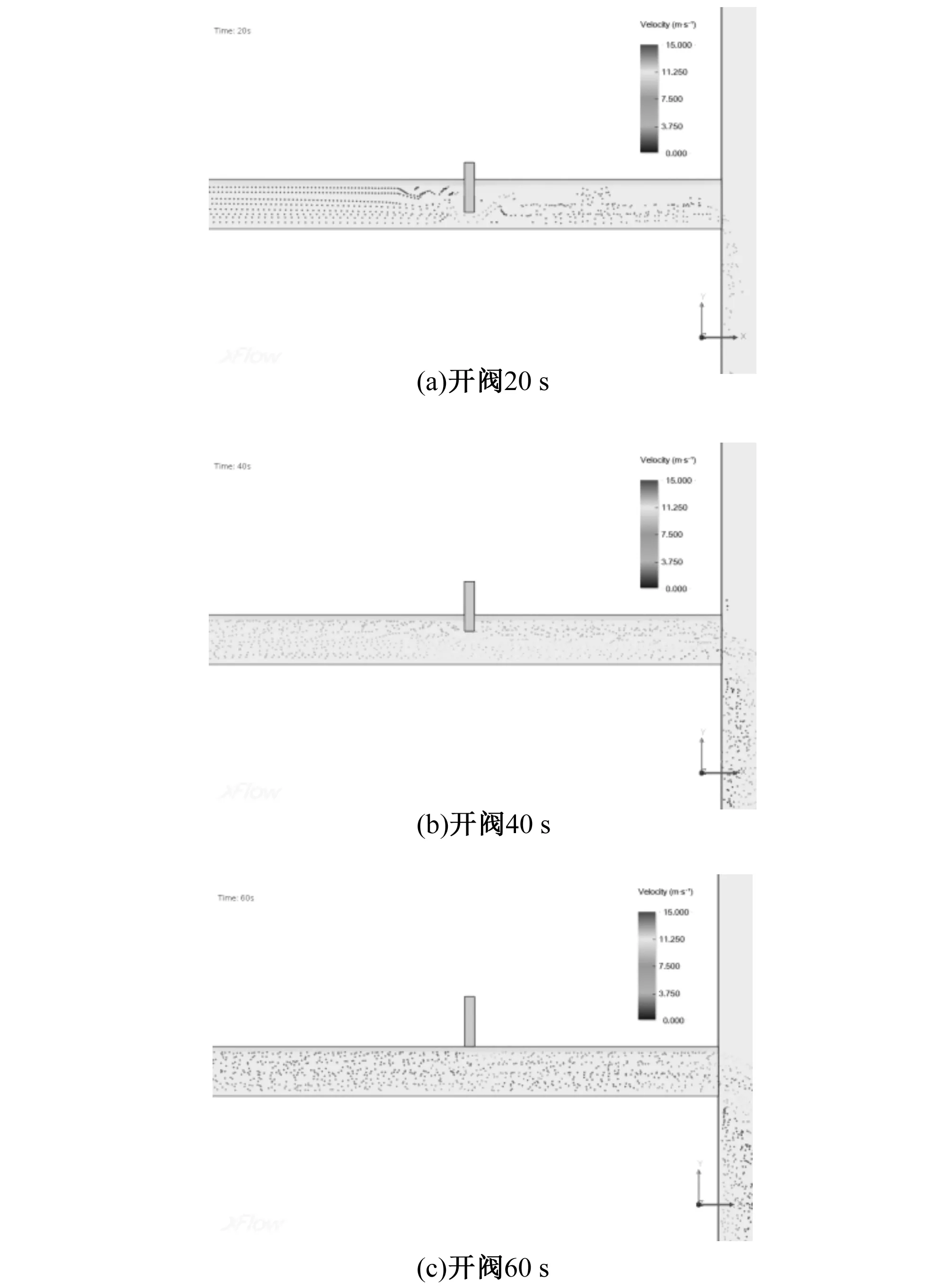
图9 开阀排空过程管内速度场变化情况Fig.9 The changing velocity distribution with the opening gate valve in draining process

取位管道出口处管轴线上的一点作为监测点，提取重力流管道排空过程中该点的压力和流速值，变化曲线分别如图10和11所示。

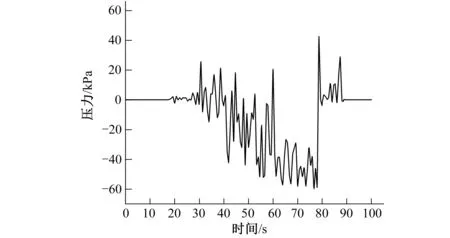
图10 排空过程监测点压力变化Fig.10 The changing pressure of monitoring point in draining process

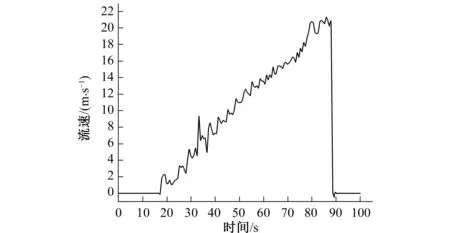
图11 排空过程监测点流速变化Fig.11 The changing velocity of monitoring point in draining process

出口闸阀离管道出口较近，受阀门启动扰动，管道出口监测点在排空过程中产生了一定的负压，但在阀门完全打开(60 s)一段时间后，在80 s左右出现快速上升并回归正值。另外，整个排空过程中管道出口流速小幅波动地上升，在89 s时流速骤降至零，说明此时管内液体已完全排空。

2.3 重力流充排水一维计算结果

为验证重力流充水和排空过程的三维瞬态计算结果，对该管道系统同时进行一维系统级别的对比计算。基于特征线法的一维管道计算不能得到管内流场变化情况，而着重求得管道重力流充水和排空过程阀后压力、流速等参数的整体变化情况，并与三维计算结果进行对比验证。管道重力流充排水一维计算模型如图12所示。

图12 重力流管道一维计算模型Fig.12 1D computing model of gravity flowed pipes

提取与三维计算对应的充水和排空过程阀后监测点的压力和流速值，变化曲线如图13和图14所示。

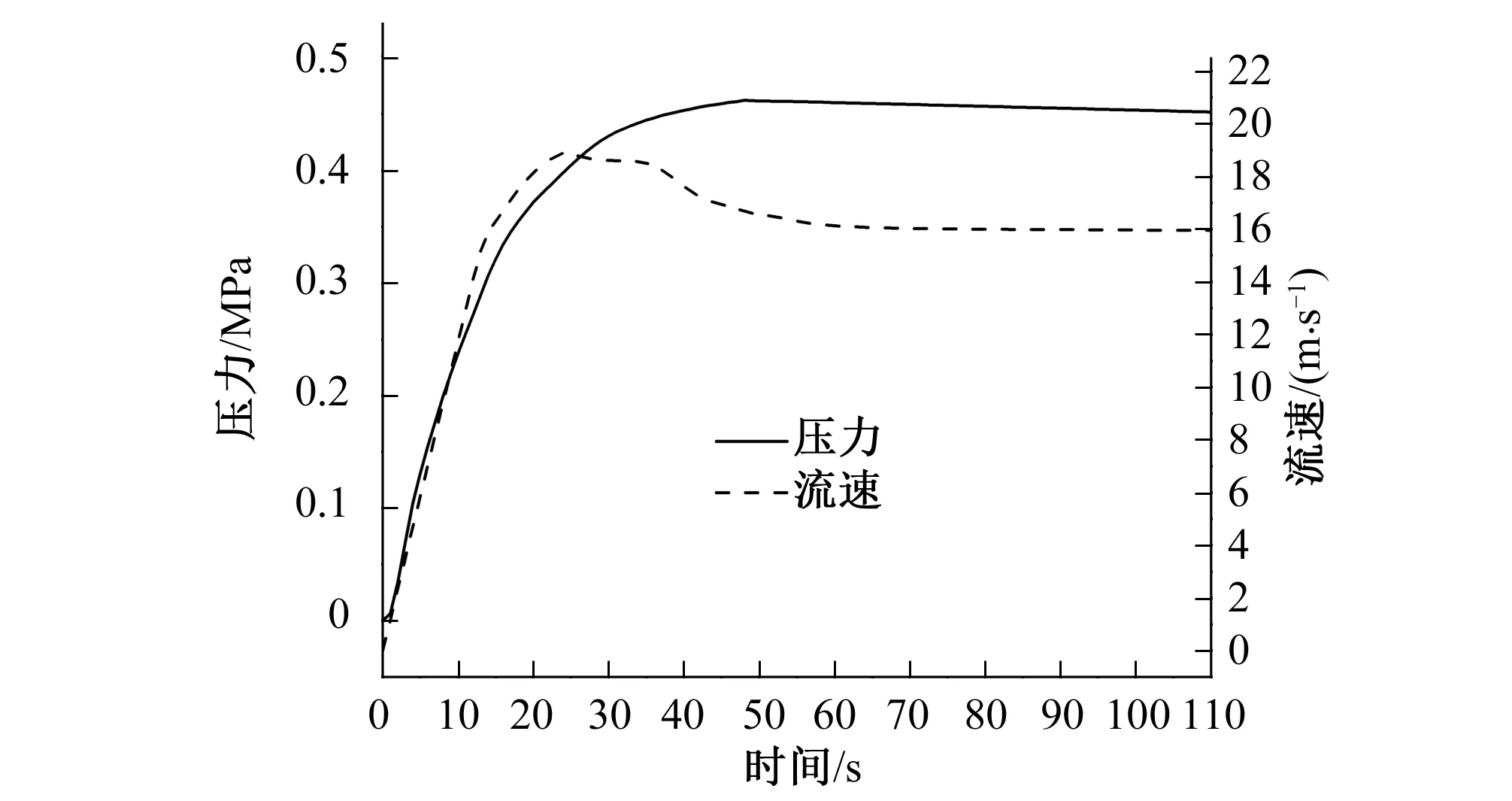
图13 充水过程监测点压力、流速变化(1D)Fig.13 The changing pressure and velocity of monitoring point in filling process(1D)

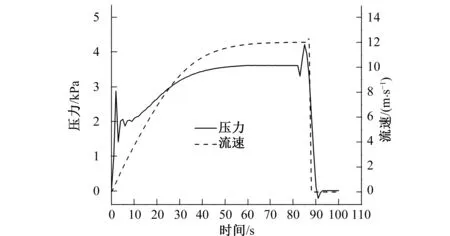
图14 排空过程监测点压力、流速变化(1D)Fig.14 The changing pressure and velocity of monitoring point in draining process(1D)

在空管充水阶段，三维计算的监测点压力在开阀50 s后快速下降，而一维计算的监测点压力在上升后保持在45 m水头左右，表明三维仿真中高位水池液面下降较一维计算快。另外，两种计算模型的监测点流速变化趋势相同，均是“快速上升-缓慢下降-平稳”的过程，两者流速最后均保持在16 m/s左右。

在满管排空阶段，三维与一维仿真相比，监测点压力波动较大；而两者流量变化趋势相同——上升至峰值后在89 s左右迅速下降至零，表明两个模型的排空时间相同。

另外，在管道重力流充水和排空的一维仿真中，压力和流速变化曲线的连续性较好，因其只考虑管轴线上的参数变化；而对应的三维瞬态模拟中参数变化过程则波动较大，体现了三维空间变化的影响。

3 总 结

本文通过无网格的格子玻尔兹曼CFD方法模拟三维管道重力流的充水和排空过程，分别得出：

(1)管道充水时管内液面变化过程和充水时间(95 s)；

(2)管道充水时进口闸阀开启过程的流态变化；

(3)管道充水时阀后监测点的压力和流速变化曲线；

(4)管道排空时管内液面变化过程和排空时间(89 s)；

(5)管道排空时出口闸阀开启过程的流态变化；

(6)管道排空时管道出口监测点的压力和流速变化曲线。

同时对相同的管道系统进行基于特征线法的一维计算，并与三维模拟结果进行对比和验证。将传统的管道系统研究由一维分析转变为三维的CFD分析是一种有益尝试，结合新型的格子玻尔兹曼算法，使流场仿真结果精度更高。

□

[1] 李 辉. 重力流压力管道输水系统的水力学问题[J]. 山西建筑，2004,(8):73-74.

[2] 杨照明，张金承. 长距离大落差重力流管道输水技术[J]. 水利建设与管理，2001,(4):12-15.

[3] 赵 鹏, 张丹丹, 汪鲁兵, 等. 格子Boltzmann并行程序的优化与性能分析[J]. 微电子学与计算机, 2008,25(10):185-188.

[4] 李 剑, 施 娟, 邱 冰, 等. 用格子玻尔兹曼方法研究粒子在涡流中的运动[J]. 桂林电子科技大学学报, 2007,(5):387-390.

[5] 刘祖斌, 赵 鹏. 结合大涡模拟的格子玻尔兹曼方法模拟高雷诺数流动[J]. 船舶力学, 2015,(5):484-492.

[6] 甘延标. 多相流系统的格子玻尔兹曼方法与模拟研究[D]. 北京:中国矿业大学(北京), 2012.

[7] Crouse B, Krafczyk M, Kuhner S, et al. Indoor air flow analysis based on lattice Boltzmann methods[J]. Energy and Buildings, 2002,(34):941-949.

[8] 王 辉. 基于格子Boltzmann方法的建筑流场仿真研究[D]. 西安:西安建筑科技大学, 2010.

[9] 韦献刚. 基于格子Boltzmann方法的地下巷道热流态仿真研究[D]. 西安:西安建筑科技大学, 2009.

[10] 丁全林, 王玲玲, 汪德爟, 等. 基于多松弛格子玻尔兹曼的弯道水流三维数值模拟[J]. 水科学进展, 2012,(4):523-528.

[11] 张 博, 王利民, 王小伟, 等. 基于格子玻尔兹曼方法的单孔射流鼓泡床的离散颗粒模拟[J]. 科学通报, 2013,(2):158-169.

[12] 许友生, 李华兵, 方海平, 等. 用格子玻尔兹曼方法研究流动-反应耦合的非线性渗流问题[J]. 物理学报, 2004,(3):773-777.

[13] 冯蕾蕾. 基于格子Boltzmann方法的复合材料微尺度传热特征研究[D]. 兰州: 兰州大学, 2009.

[14] 李 强, 余 凯, 宣益民. 纳米流体流动与传热过程的LBM并行计算[J]. 南京理工大学学报(自然科学版), 2005,29(6):631-634.

[15] 刘新伟. 重力流管道管径设计[J]. 化工设计, 2004,(2):20-22.

[16] 陶文铨. 数值传热学[M]. 2版. 西安：西安交通大学出版社, 2001.

[17] 段欣悦. 格子玻尔兹曼方法的理论研究与应用[D]. 青岛: 中国石油大学(华东), 2006.

[18] Qian Y H, Humieres D D, Lalleman P. Lattice BGK models for Navier-Stokes equation[J]. Europhysisc Letters, 1992,17(6):479-484.

[19] 陶 实. 格子玻尔兹曼方法在计算流体力学中的应用研究[D]. 辽宁大连:大连理工大学, 2013.