山区河流影响下的城市防洪避难安置点理论研究

范 强，田 忠，李 南，丁 灿，唐南波，王启艳

(四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065)

0 引 言

城市是某一地区范围内的政治、经济和文化中心，一旦遭遇自然灾害的侵袭，势必将会造成巨大的人员伤亡和财产损失。随着我国城市发展的不断加快，越来越多的人员及财富源源不断地涌入城市。当遭遇严重的自然灾害，尤其是洪水灾害时，城市防洪的脆弱性就暴露无遗。对于可能会被洪水侵袭的城市来说，科学、合理地规划建设一批城市防洪避难安置点已成为城市发展的迫切要求。如果没有一批安全的城市防洪避难安置点，在发生洪水灾害时，将会导致严重的人员伤亡与财产损失。

我国是一个多山地国家，山区面积占到了国土陆地总面积的2/3。山区河流因其具有独特的特点，在暴雨期汇流速度快，能在较短时间内形成大规模洪水。而且，我国众多的山区河流上往往建设有水电站，若洪水冲垮大坝，溃坝洪水将对下游城市造成毁灭性打击；即使大坝不垮，洪水期大坝开闸泄洪，也会对下游城市造成巨大破坏。本研究主要针对山区河流影响下的城市防洪避难安置点的预警分级、选址原则及安置点规划进行研究，文中提出了相应的数学模型并对其进行了优化。

1 应急避难安置点的预警分级

应急避难安置点是经过科学规划建设与规范化管理，在遭遇灾害后能够为灾民提供最基本的生活条件、能够安全避难、等待救援及相关部门指挥调度救灾的场所。由于洪灾后的很长一段时间内，灾民无法回到城市中正常工作和生活，应急避难安置点就成为灾后恢复阶段保障灾民基本生活的临时性场所[1]。

根据我国山区河流影响下的城市防洪应急避难的特点，通常将这些地区的安置点划分成紧急避难安置点、固定避难安置点及中心避难安置点3级。紧急避难安置点为灾民提供临时避难，是人群聚集并转移到其他安置点的过渡性场所；固定避难安置点是提供长时间避难和庇护的场所，一般为面积较大、人员容量较大的场地空间。中心避难安置点是救灾物资、救灾人员、医疗设备及伤员的转运中心。

2 应急避难安置点的规划原则与要求

山区河流影响下的城市防洪避难安置点[2,3]的选择应引入科学的规划方法进行布局，使有限的安全保障资源最大限度地为灾民提供避难服务。避难安置点应选择地势较高、交通较为便利处，所属的配套设施应尽可能齐备，包括：避难生活设施、指挥和通信设施、疏散保障设施、医疗救护设施及运输场地设施等。避难安置点的规划选择及空间配置，应充分考虑以下几个原则。

(1)安全原则：这也是选择防洪避难安置点最重要的原则。安置点应远离易燃易爆化学物品、核放射物、高压输电线路、地下断层、矿山采空区、岩溶塌陷区、地震断裂带等。同时，要保证避难安置点不会被洪水淹没，地势应平坦、开阔，易于搭建临时住房，并有相对较好的内外交通条件，有较高的物资供应能力以及最基本的生活设施等。

(2)就近避难原则：应急避难安置点的建设要坚持就近布局的原则，安置点的布局、数量要尽量与灾民避难要求相协调，在灾害发生后能使灾民迅速转移至安置点。

(3)合理选址原则：要确保避难点不受洪水侵袭，不能让灾民做多次搬迁；同时安置点高程选择也不能太高，其地面高程只要高于“洪水位+安全超高”即视为安全，这样既方便建设，也方便救灾物资的运输。

(4)综合防灾、统筹规划原则：安置点要与山区平整地规划相协调，在功能上要实现平、灾结合、一所多用，这样既能节约建设成本，也能极大地节省占地面积。

(5)可持续发展原则：避难场所可持续发展的关键是要与避难场所的资源承载能力相协调，要控制好安置区内的人口数量，使人口维持在资源承载力所能接受的范围之内。

3 防洪避难安置点数学模型的建立与求解

3.1 防洪避难安置点的规划布局

防洪避难安置点在规划阶段要解决的问题是：某一城市的人口基数、人口密度及城市所有道路网数据已知的条件下，在所有可能作为避难安置点的场所中选择部分地点作为防洪避难安置点。这主要是由于环境要求及资金限制，不能在所有能够建立避难安置点的场所都设立安置区，在实际规划建设中只能优选部分地点来建设。

防洪避难安置点的规划与建设问题属于公共设施区位问题的一种，即：已知某一地区公共服务设施分布的位置，充分考虑人群对公共服务设施数量的需求，确定公共服务设施的最佳布局方式。目前，为解决这类问题，一些学者提出p-中位数法、极大熵法、区位覆盖模型及最大覆盖模型等多种解决方案。其中p-中位数法的解决思路是把公共服务设施的区位问题抽象成：在M个区位备选地点中选择p个区位用以建设公共服务设施，使得所选区位距离总的加权平均值最小。p-中位数法可以同时控制公共服务设施的影响范围和位置；而且，p-中位数法算法简单，运算快捷，控制变量较少，当公共服务设施数目一定时，p-中位数法是唯一而有效的配制方法[4]。

由于p-中位数法具有以上所述的众多优点，因此被广泛应用于公共服务设施的区位划分问题。Hanif等人在解决飓风灾害下的人员疏散避难逃生问题中提出了解决这类问题的数学模型，即：在已知的可用于规划建设避难安置点的场地内选择若干地点用于人员的疏散规划，其目标函数是灾民撤离总路径最短[5]。本研究在防洪避难安置点的规划研究中也采用类似的方法。

3.2 p-中位数法模型

p-中位数法在1964年由Hakimi首次提出[6]，该方法假定所有设施区位节点为潜在可用的中位数，定义V为节点，A为边，从而得到无向图集合G=(V,A)；p-中位数法的优化目标是寻找中位数集合，使得(V-Vp)中剩下的节点与Vp中最近的节点距离之和为最小。在上述假设中，每个节点可以同时作为需求点与提供服务的设施点。因此，典型的p-中位数法目标函数可以表示为：：

(1)

约束条件为：

(2)

xij≤yij,i,j=1,2,…,n

(3)

(4)

xij,yj∈{0,1},i,i=1,2,…,n

(5)

此p-中位数法模型每个需求区位节点都由相应的公共服务设施提供服务。(1)式为目标函数，是需求节点集合与中位数集合间的加权距离之和；(2)式为约束条件，是为保证每个需求点都有设施点向对应；(3)式同样为约束条件，禁止需求节点与未被选为中位数的设施点相对应；(4)式为中位数节点个数；(5)保证控制变量x，y取值仅为0或1。

该典型p-中位数法的基本假设为：

(1)各分区有且仅有唯一的区位服务设施，各设施的服务容量假定没有任何限制；

(2)p个区位设施均能够提供基本相同的服务，同时需求者对分区没有选择偏好，均以距离的远近作为基本选择依据；

(3)分区规模相对均匀，规模不影响需求，由人群需求决定设施规模；

(4)人员行动理性，能够利用最短路径向区位服务设施转移，同时路况不会发生变化。

由于公共服务设施区位模型假定的各设施点能够无限制的容纳人员，也就意味着各防洪避难安置点的容量无限，这很明显与实际情况存在较大出入。在实际避难逃生中，每个安置点能够容纳的灾民人数都有上限，当某一避难安置点的灾民人口数达到人员安置上限时，就不能提供避难服务。因此，在传统p-中位数法的数学模型中应根据实际情况添加约束条件：各区位服务设施安置点只能满足各自有限数目需求点的避难要求。

3.3 基于遗传算法的求解方案

实际情况中，在确定避难安置点的数目和选址时，必须考虑相关约束条件，然后再根据不同城市的具体情况确定最优防洪避难安置点的规划方案，考虑目标函数需求节点集合与中位数集合间的加权距离之和最小，在一定范围内求出p个避难安置点的最优位置。启发式算法是求解p-中位数法最常用的方法之一，首次提出启发式算法的是Bart和Teitz[7]，启发式算法基于节点交换过程，在迭代过程中逐渐增大目标函数值，该方法简单易行，能得出比较准确的结果。考虑到避难安置点位置规划与建设问题的特点，节点数目众多，目标函数复杂，求取近似解就能够满足实际规划要求。

遗传算法属于启发式算法的一种，主要用于解决复杂的优化问题。遗传算法模拟生物的进化过程，通过对染色体进行编码以得到初始种群，再通过筛选、基因交换及基因变异等操作进行下一代种群的繁殖，并必须要保证后代基因优于父代基因，在迭代数次后就能够得到最优解。遗传算法求解p-中位数问题的重点在于确定编码方案及遗传操作与遗传参数的确定。

本研究对避难安置点优选设计的遗传算法中，采用长度为l的二进制整数进行编码，将长度为l的二进制数编码形成十进制数。十进制数就是需求点所在矩阵的行位置。假定存在n个需求点，就会存在n个长度为1的二进制基因组，将n个基因组合成长度为l×n的染色体序列。选择算法采用轮盘赌法，应用“适者生存”的原则进行进化方案的优选，即具有高适应值的特征字符串将会以更大的概率传递到下一代，适应度函数越大，被选中的概率也就越大。实际运算证明本研究设计的遗传算法能有效地求解防洪避难安置点的规划问题[8]。

4 p-中位数法结合安置点加权评分优化模型

在有容量限制的p-中位数模型中，比较难以解决的是需求点与设施点的节点分配问题，即：当避难安置点达到容量限制后，本应分配到此安置点的灾民需进行再分配，根据就近原则一般分配到第二近的安置点，如果第二近的安置点仍已满，分配到第三近的安置点，依此类推，直到找到人员未满的安置点为止。p-中位数法选择不同公共设施节点会对目标函数产生影响，以往的研究中并未解决此问题。本研究在分析前人研究成果的基础上，开创性的提出的p-中位数法结合安置点加权评分优化模型是对p-中位数法的进一步完善和创新。

防洪避难安置点的主要作用就是保障灾民的生命安全，其安全性十分重要。它应具备多方面的条件，除尽可能选取较短的逃生路径外，地质地形条件、场地可利用空间、场地安全状况等都是必须考虑的问题。因此，若要保证防洪避难安置点的可靠性就必须对p-中位数法进行优化。

本研究利用“6因子评价法”对避难安置点进行综合性评价。即在众多备选安置点中选用：地质地形条件F1、救灾道路状况F2、场地可利用空间F3、场地安全状况F4、基础设施状况F5及是否可持续发展F6这6个评价指标对应急避难安置点进行综合评判，每个因子评为：极差(1分)、较差(2分)、一般(3分)、好(4分)、极好(5分)5个分数等级，避难安置点的评价指标和评分标准见表1。

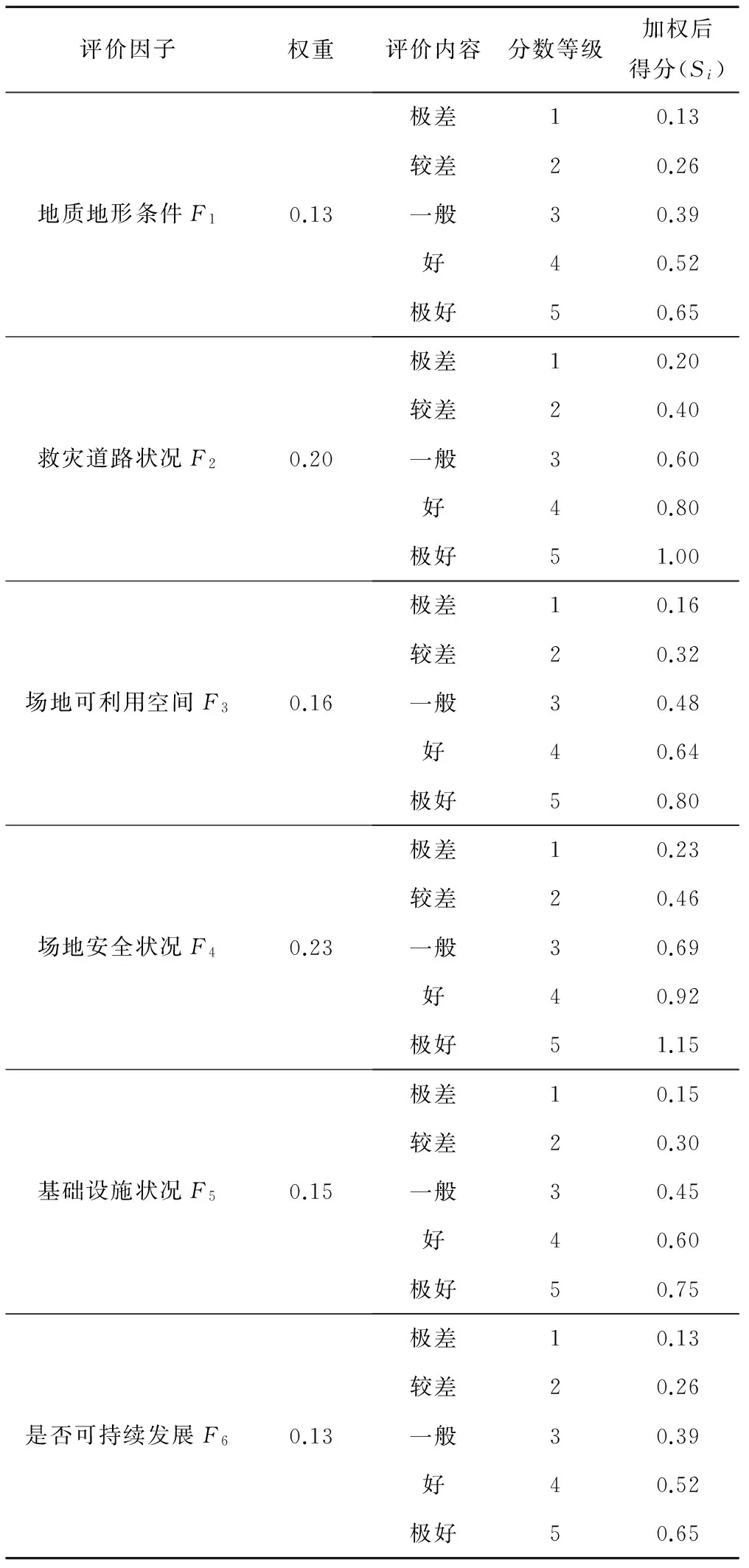
表1 避难安置点评价指标和评分标准Tab.1 Evaluation criteria and score of UEES

在对避难安置点进行选择时，参考表中不同评价因子对应评价内容的加权得分，将这6个加权得分相加得到：

wij=∑Si,i=1,2,…,6

(6)

从N个候选的安置点中任选p个作为初

始解，同时将wij带入式(1)，得到优化后的目标函数的初始值Z0：

(7)

从其余(M-p)个安置点中选择一个节点，轮流替换初始解中的每个节点，并分别计算Z值，将每个Z值与Z0进行比较，找出最小值，选定该值对应的解为新的最优解，重复上述两个步骤，直至最小Z值不再发生变化时，此时的解为最优解。

5 结 语

文章对我国山区河流应急避难安置点的规划原则与要求进行了概述，开创性地提出了p-中位数法结合安置点的加权评分优化模型，对传统的p-中位数理论进行了完善和创新。防洪避难安置点的研究在我国刚刚起步，本研究所提出的理论及模型仍处于基础研究阶段，在接下来的研究中将综合考虑更为复杂的因素，使防洪避难安置点的研究更臻完善。

□

[1] 姚清林.关于优选城市地震避灾场地的某些问题[J].地震研究, 1997,19(3):244-248.

[2] 杨文斌, 韩世文, 张敬军,等.地震应急避灾场所的规划建设与城市防灾[J].自然灾害学报, 2004,13(1):126-132.

[3] 苏幼坡.城市地震避难所的规划原则与要点[J].灾害学, 2004,19(1):87-92.

[4] 黄河潮, 林 鹏, 卢兆明.p-中位数法在城市应急避难所规划中的应用[J].应用基础与工程科学学报, 2004,(S):62-66.

[5] Hanif D S, T B C Antoine G H. A Location-allocation model and algorithm for evacuation planning under hurricane/flood conditions [J].Transportation Research Part B-Methodological, 1991,25(6):373-478.

[6] Hakimi S L. Optimum location of switching centres and the absolute centres and medians of a graph [J].Operations Research, 1968,(34):450-459.

[7] Teitz M B, Bart P. Heuristic methods for estimating the generalized vertex median of a weighted graph[J]. Operations Research, 1964,(12):450-459.

[8] 潘安平.基于遗传算法的台风避难所选址模型研究[J].财富网络, 2009,(4):35-38.