竖井地基热排水固结模型试验

刘干斌，范高飞，陶海冰, 2，尹铁锋，邓岳保



竖井地基热排水固结模型试验

刘干斌1，范高飞1，陶海冰1, 2，尹铁锋1，邓岳保1

(1. 宁波大学岩土工程研究所，浙江宁波，315211；2. 浙江大学滨海和城市岩土工程研究中心，浙江杭州，310027)

设计竖井热排水固结模型试验系统，选取宁波地区典型软黏土，在室温和水热循环温度70 ℃下分别开展排水固结和热排水固结模型试验，分析加热、分级堆载、恒载降温阶段各测点的温度、孔隙水压力及地表沉降变化规律。研究结果表明：热排水固结法可加速地基模型的固结速率，固结度达到90%所需时间较排水固结法所需时间减少；经过温度历史后，地表最终沉降量增加，土的抗剪强度有所提高，增强软基处理效果。在试验基础上，分析热排水固结法作用机理，结合已有先期固结压力随温度变化理论，按−lg曲线法建立热排水固结法的沉降计算公式，并对竖井模型地表沉降进行计算，与试验结果吻合较好，初步验证公式的合理性。

热排水固结；模型试验；竖井地基；−lg曲线；沉降

热排水固结法是近几年国际上出现的软基处理新方法。与排水固结法相比，热排水固结法在竖井中插入U型导热管，并将导热管中的水加热至一定温度，实现管−土之间的热传递，以提高竖井周边土的渗透系数，加速地基排水固结，是解决沿海地区低渗透性软土地基采用常规排水固结法处理周期长这一技术难题的有效途径之一。POTHIRAKSANON等[1]采用该法处理曼谷路基的黏土地基。近年来，国内外学者对土的热固结问题开展了诸多研究。例如TIDFORS等[2]利用单向固结试验，对不同温度下瑞典黏土的固结变形特性进行了研究，发现温度变化影响土的先期固结压力。BOUDALI等[3]的试验也表明：温度对天然软黏土的先期固结压力、压缩曲线、孔隙水压力有较大影响。TOWHATA等[4]开展了黏土的温控固结试验，结果表明：升温可使土的结构性破坏，从而提高土的渗透性。SULTAN等[5]利用温控GDS三轴仪开展了不同温度下Boom黏土试验，试样体应变随温度升高而增大，并给出了先期固结压力与温度变化的关系式，分析了超固结比对体变的影响。ABUEL-NAGA等[6]通过试验建立了温度与土的体变关系。ROMERO等[7]研究认为饱和度75%以下时，温度对土的渗透系数无明显影响，当饱和度大于75%时，土的渗透系数随温度升高而增大。温度对土的渗透性的影响，不能仅归因于孔隙水表面张力受温度的影响，还需考虑热对土结构性的扰动和孔隙流热化学变化。TSUTSUMI等[8]利用温控固结渗透仪器研究了饱和土的固结性状，并从黏滞性角度对试验现象进行了解释。此外，吴瑞 潜[9]和白冰[10]基于饱和土体热固结方程，给出了温度与孔压的解析解。陶海冰等[11]对一个经典有涂抹区的竖井地基进行计算，分析了不耦合温度、耦合温度但不考虑其对饱和土物性影响、耦合温度考虑温度对饱和土渗透性影响计算结果的异同，初步揭示了软土地基的热−水−力耦合作用机理及热排水固结软基处理的温度效应。当前，模型试验已成为研究软基处理问题的最有效手段之一。王安明等[12]进行了广州国际会展中心动力排水固结软基处理室内模型试验，重点分析了插设塑料排水板过程、全部夯击过程及夯击完成后软黏土的孔压响应。王柳江等[13]针对海相吹填土的特点，提出了采用真空预压联合电渗法的地基加固方法，并通过室内模型试验对该工法的加固机制进行了初步探索。闫澍旺等[14]进行了超软土真空预压室内模型试验，提出了对超软土地基进行二次加固的工艺可使超软吹填土产生较好的加固效果。余飞等[15]进行了软土电化学桩加固的室内模型试验，探讨了电化学桩加固的电解特性及主要控制参数，并对胶结桩体强度分布规律、承载力特性和水稳性进行了研究。由于竖井热排水固结过程是一个多物理场耦合发展变化过程，其作用机理较为复杂，国内外有关土的热固结研究并不能直观地、全面地揭示竖井热排水固结法作用机理。而原型试验又受到施工、场地等因素影响不易开展，且试验耗资大。为了探索竖井热排水固结法作用机理，评价其加固效果和适用性，开展竖井地基热排水固结模型试验，是一种可行的、合理的手段。为此，本文作者设计了竖井热排水固结模型试验系统和试验方案，并选取宁波典型软黏土开展竖井地基排水固结与热排水固结模型试验对比研究，得到地基土的温度、孔压和沉降发展变化规律，分析评价了热排水固结法处理效果，并建立了考虑温度变化的沉降简化计算公式。

1 试验系统和内容

1.1 试验系统

竖井热排水固结模型试验系统包括反力架、杠杆加载装置、模型试验桶及电脑式水循环加热器4个部分。反力架包括底架与门式框架，均由工字钢焊接而成，用于承受竖井地基加载所引起的反力；杠杆加载装置由横梁、吊杆、砝码及带油压表的千斤顶等组成，用于加载及测量加载压力；模型试验桶为不锈钢板焊接而成的圆桶，顶部开口；电脑式水循环加热器以水作为传热媒体，通过电热加温及热水泵强制循环，可控制进入U型导热管的水温，温控范围为室温 ~120 ℃。

1.2 试验方案

试验期间，室内昼夜温度在28.0～29.2 ℃之间变化，水循环温度设定为70 ℃。试验步骤如下。

1) 地基分层填筑。先将PVC管(直径70 mm、高度1.2 m)、U型导热管(外径20 mm、内径16 mm)在桶中央固定，再分5次往桶内填筑黏土，每层土样虚高25 cm，在15 kPa压力下静压至沉降稳定后再填筑下一层。土样填筑完成后，在PVC管中灌入中砂，压实后拔出PVC管，形成竖井，并在黏土顶部填筑10 cm厚中砂垫层作为水平排水通道，从而形成竖井地基模型。将竖井地基静置168 h后再开展模型试验，模型示意图如图1所示。

2) 传感器埋设。在布设传感器前，基于非等温管道流理论及THM耦合理论，利用COMSOL多物理场软件对竖井地基模型进行加热模拟，在模型温度稳定后，发现图1所示的U型管平面内和其垂直平面内各相同位置点的温度差异较小，故仅在顶部和底部附近竖井平面和垂直平面内布设2组4个温度−孔压一体式传感器，以观测相关点的温度和孔压变化规律。传感器孔压量程为0~0.3 MPa，误差0.1 kPa；温度量程0~80 ℃，误差±0.1%。在填筑第2层、第4层土样后，埋设传感器，其中1和2号传感器置于U型管所在平面内，距桶底25 cm，距竖井边缘依次为14.5和4.5 cm。3和4号传感器位于U型管垂直平面内，距桶底75 cm，距竖井边缘依次为14.5和4.5 cm。在模型土体表面设置沉降板，以测定地表沉降量。

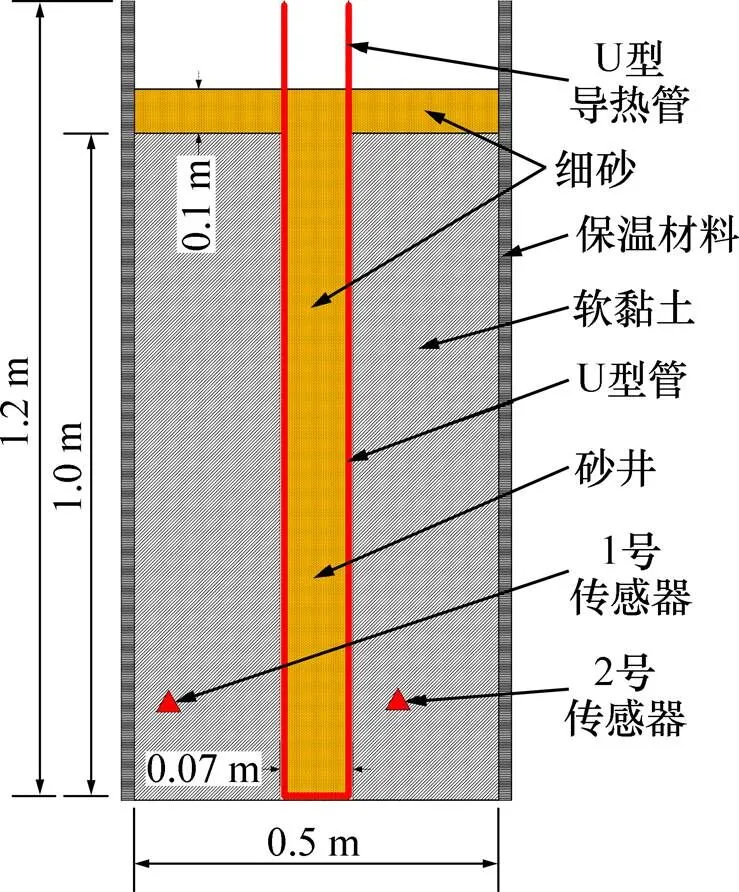
图1 竖井地基示意图

3) 无堆载加热。在模型桶外部黏贴保温材料，连接U型导热管和电脑式水循环加热器，将温度设定为预定值(70 ℃)，开启电脑式水循环加热器，对土样进行循环加热，加热时长以传感器温度趋于稳定为限。排水固结模型试验无此步骤。

4) 分级堆载。为了反映加热阶段地基的热固结机理，本试验设定加热引起的孔压消散和沉降稳定后，再分三级进行堆载，每级压力为25 kPa，待每级压力下孔压消散、沉降稳定后方可进行下一级堆载，堆载过程可停止加热或持续加热(电脑式水循环加热器自行调节，间歇式加热，保持试验过程温度恒定，耗电量较少)，为评价热排水固结法作用效果，本文采用持续加热模式。排水固结模型试验在竖井地基静置168 h后即进行分级堆载，要求同上。

5) 恒载降温。待第3级堆载作用下孔压消散、沉降稳定后，关闭电源，停止水循环加热，并去除模型箱外侧的保温材料，使土样自然降温至室温，至此热排水固结模型试验完成。排水固结模型试验无此步骤。

1.3 测试内容

利用1~4号温度−孔压一体式传感器测定地基温度和孔隙水压力，利用沉降板测定各级加载引起的地表沉降数据。

2 试验结果分析

2.1 温度

在室温条件下，排水固结模型试验过程中1~4号传感器的温度时程曲线如图2所示；水循环温度为70 ℃条件下，热排水固结模型试验过程中1至4号传感器的温度时程曲线如图3所示。由图2可知：排水固结模型试样温度随室温变化而变化，室温温度范围为28.0~29.1 ℃，平均室温约为28.6 ℃，4个传感器温度随时间变化与室温变化基本一致，但埋设位置不同，土层温度与气温升降之间存在滞后，1和2号传感器温度总体较3和4号传感器温度低，同一时刻各传感器间的最大温度差约为0.4 ℃。

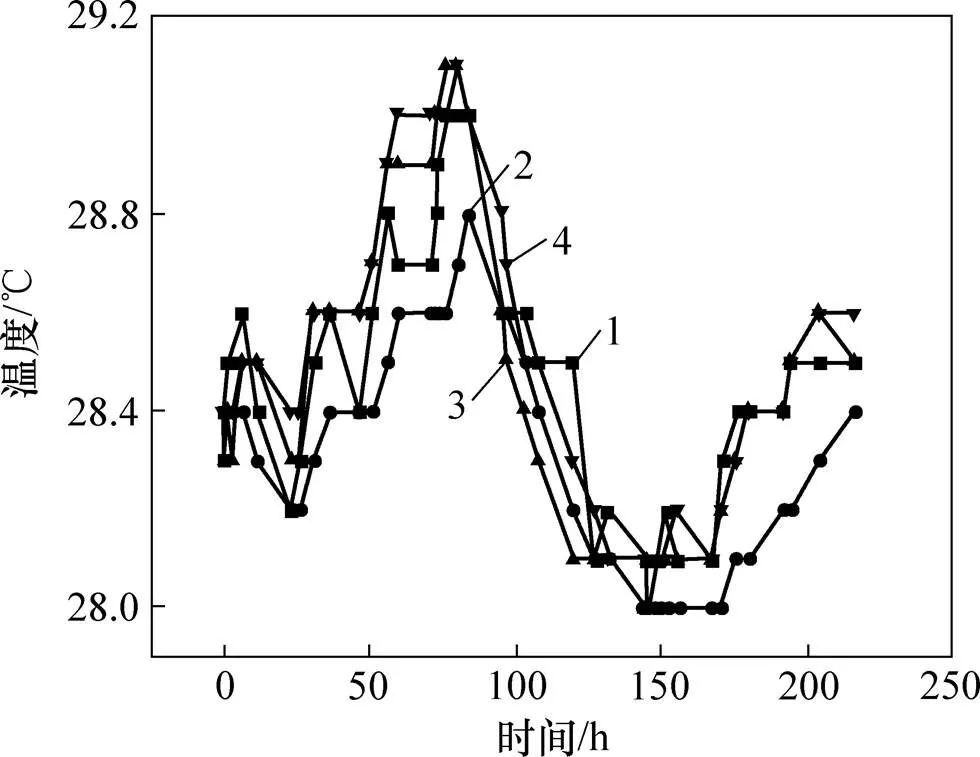
传感器编号：1—1号；2—2号；3—3号；4—4号。

由图3可知：无堆载加热(本阶段0~216 h)48 h左右地基温度趋于稳定，但为了观察加热引起的超静孔压的消散过程，再持续加热168 h，加热总时长为216 h。土体温度增长至最大值(1~4号传感器温度最大值依次为56.8，60.6，55.9和60.3 ℃，平均值为58.4 ℃)，并保持稳定。分级堆载阶段(216~432 h)，土体温度仍稳定于最大值，并未因堆载、渗流产生较大变化；恒载降温阶段(432~480 h)，土体温度由最大值快速降至室温。在热排水固结模型试验中，底、顶部1和3号传感器温度差为0.9 ℃，2和4号传感器温度差为0.3 ℃，且底部温度较顶部温度高，系由于模型桶顶部开口，有一定的散热作用，与填筑土层的均匀性也有一定的关系。可见，由于加热管道有进水口与出水口，土样温度不是轴对称分布，但管井比足够小(0.2)，为便于理论、数值研究，温度场可简化为轴对称分布。

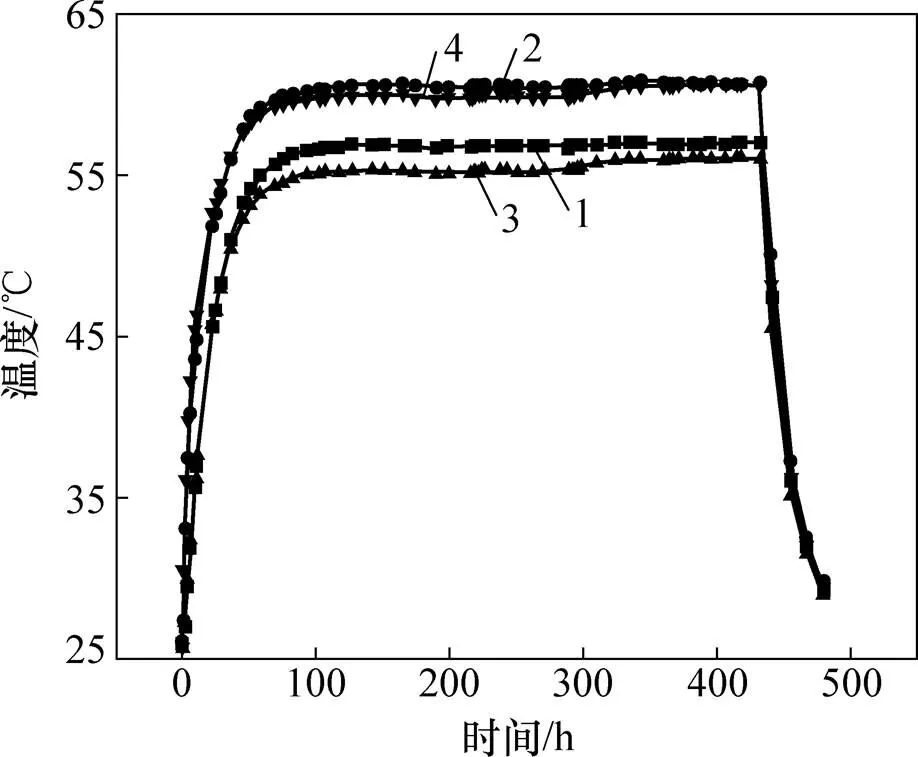
传感器编号：1—1号；2—2号；3—3号；4—4号。

2.2 孔隙水压力

在室温条件下，排水固结模型试验中孔压时程曲线如图4所示。由图4可以看出：每级堆载压力下(25 kPa)，孔压快速增长至峰值(孔压增量为10~20 kPa)，随后逐渐消散至稳定，消散速率随固结发展逐渐减慢。堆载压力越大，残余孔压也越大，1~4号传感器残余孔压依次为5.8，3.5，6.8和7.8 kPa。

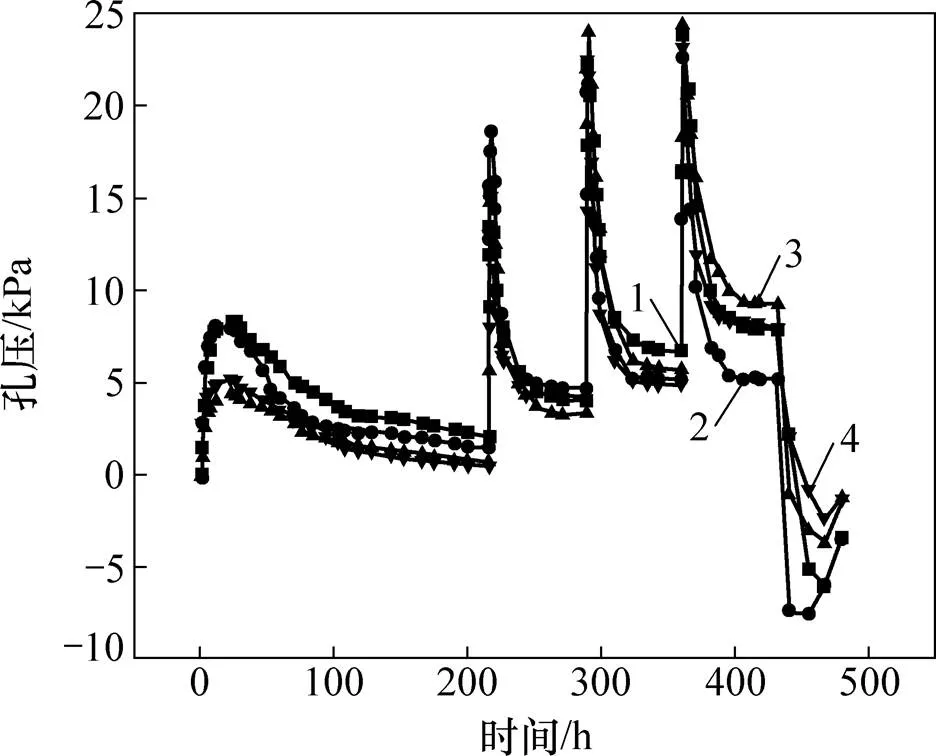
在水循环温度为70 ℃条件下，热排水固结模型试验中孔压时程曲线如图5所示，在无堆载加热阶段(0~216 h)，孔压在0~24 h内增长至极大值(孔压增量为4.1~7.9 kPa)，随后缓慢消散至稳定值；分级堆载阶段(216~432 h)，孔压发展变化规律类似于排水固结模型试验；恒载降温阶段(432~480 h)，残余孔压(1~4号传感器残余孔压依次为7.9，5.2，9.3和8 kPa，平均值为7.6 kPa)迅速减小至负值(1~4号传感器最大负孔压依次为−6.0，−7.5，−3.6和−2.3 kPa)，随后又逐渐增大，但孔压最终为负(1~4号传感器最终孔压依次为−3.4，−3.4，−1.2和−1.3 kPa，平均值为−2.3 kPa)。

从单个传感器得到的孔压结果来看：在无堆载加热阶段，其孔压发展过程与该点温度发展有关，一方面因为温度的增长导致孔压增长，另一方面由于排水使孔压消散。当温度增长速率导致的孔压增长速率大于孔压消散速率时，孔压将会增长；当孔压增长速率小于孔压消散速率时，特别是当温度达到恒定时，孔压增长速率为零，孔压将消散。

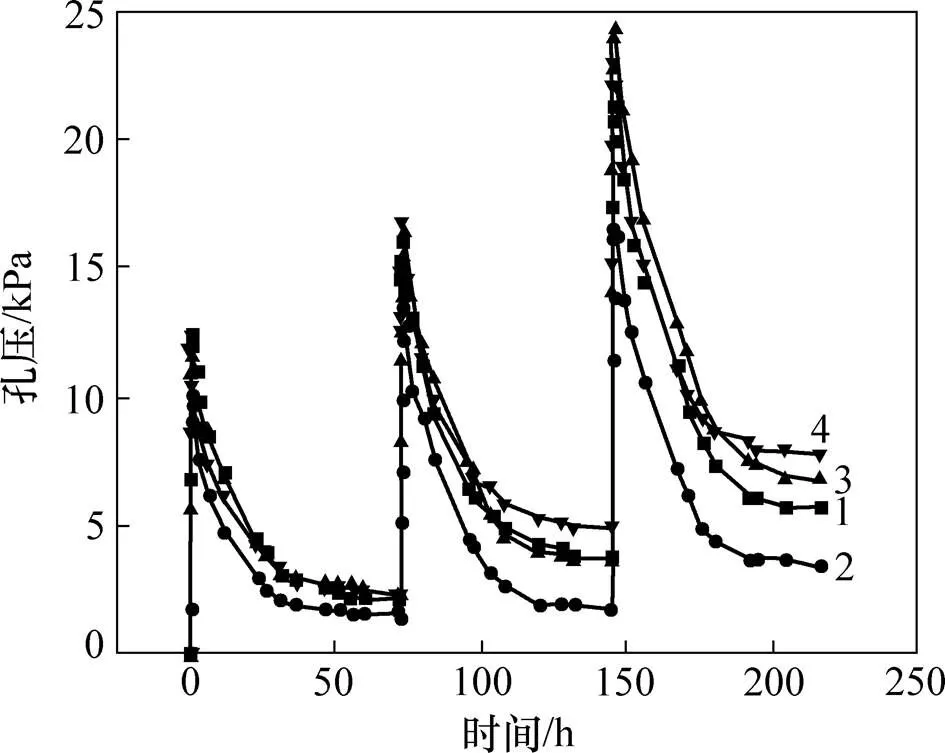
传感器编号：1—1号；2—2号；3—3号；4—4号。

传感器编号：1—1号；2—2号；3—3号；4—4号。

在堆载阶段，每级荷载加载时，在传感器所在深度，孔压增量达不到堆载增加值。这种现象的产生很大程度上是因为模型桶的尺寸效应，土体与模型桶壁产生的摩擦，使得部分堆载压力扩散到筒壁上，尽管桶壁做了光滑处理（抛光、涂凡士林），摩擦效应有一定减少，但无法消除，且由于摩擦效应的存在，位置越深的土体堆载压力扩散越大，应力作用越小，加载瞬间的孔压增量也越小，这一现象在试验结束卸土时发现的越接近桶底的土越软得以证实，有待于大尺寸模型试验或原位试验来消除。

另一方面，无论排水固结或热排水固结，每级堆载所引起的孔压难以完全消散，有较大的残余孔压，且残余孔压随着堆载级数的增加而增大。产生残余孔压的现象的解释很多，作者认为其产生可以用非达西渗流理论[16]来解释，存在1个水力梯度的阈值，如果土体中某点水力梯度小于该阈值，其渗流速度极速减小甚至为0，而且该阈值会随着孔隙比减小而增加，从而较好地揭示了残余孔压随堆载级数增加而增大的现象。在热排水固结法的恒载降温段，降温能使残余孔压迅速消散，土体有效应力增加，使得土体继续沉降压实。

2.3 地表沉降

模型试验地表沉降曲线如图6所示，分级堆载产生的地表沉降对比曲线如图7所示。由图6可知：每级压力下，地表沉降先有一瞬时变化值，后逐步发展，并趋于稳定，三级堆载下地表沉降依次为23.48，21.12和18.88 mm，在相同堆载压力下地表沉降依次减少，最终累积沉降为63.48 mm。热排水固结模型试验无堆载加热阶段(0~216 h)，地表先逐渐隆起(最大隆起值2.15 mm)，随后又逐渐下沉至稳定(最大沉降2.65 mm)；分级堆载阶段，沉降发展变化规律类似于排水固结模型试验，三级堆载下地表沉降依次为24.85，23.18和19.57 mm，堆载压力作用下的总沉降量为67.60 mm；恒载降温阶段，地表沉降逐渐变大(恒载降温阶段的沉降为7.00 mm)，热排水固结模型试验地表最终沉降为77.25 mm，较排水固结法增大了21.7%。

由图7可知：每级堆载压力下，热排水固结模型试验的沉降发展较排水固结模型试验变快，且三级堆载作用下排水固结模型试验的沉降为63.48 mm，热排水固结模型试验的沉降为67.60 mm，较前者增大6.5%。

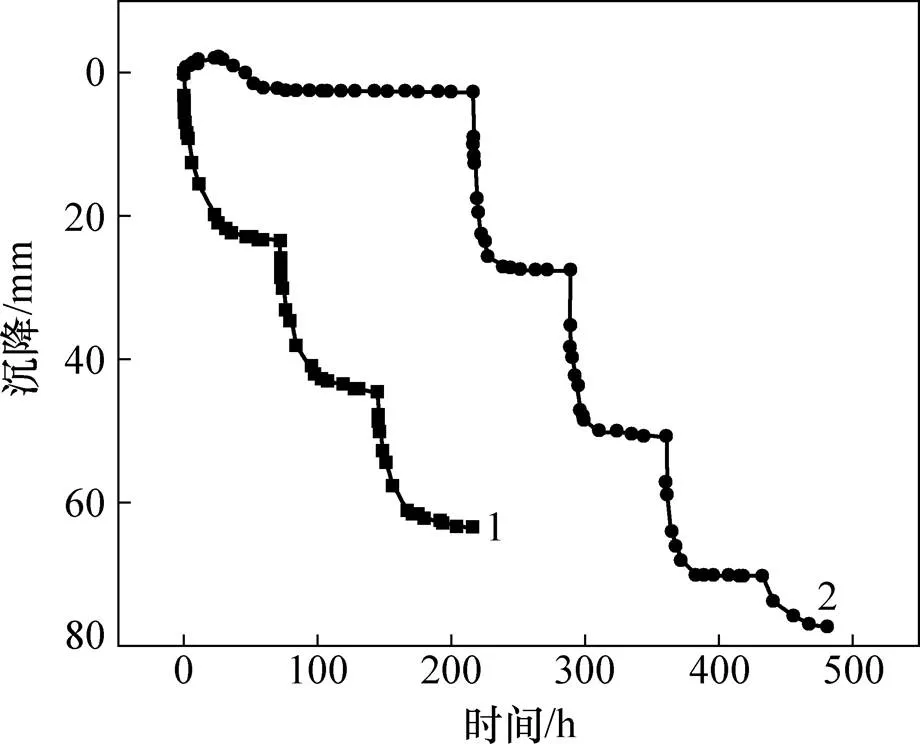
1—传统排水固结；2—热排水固结。

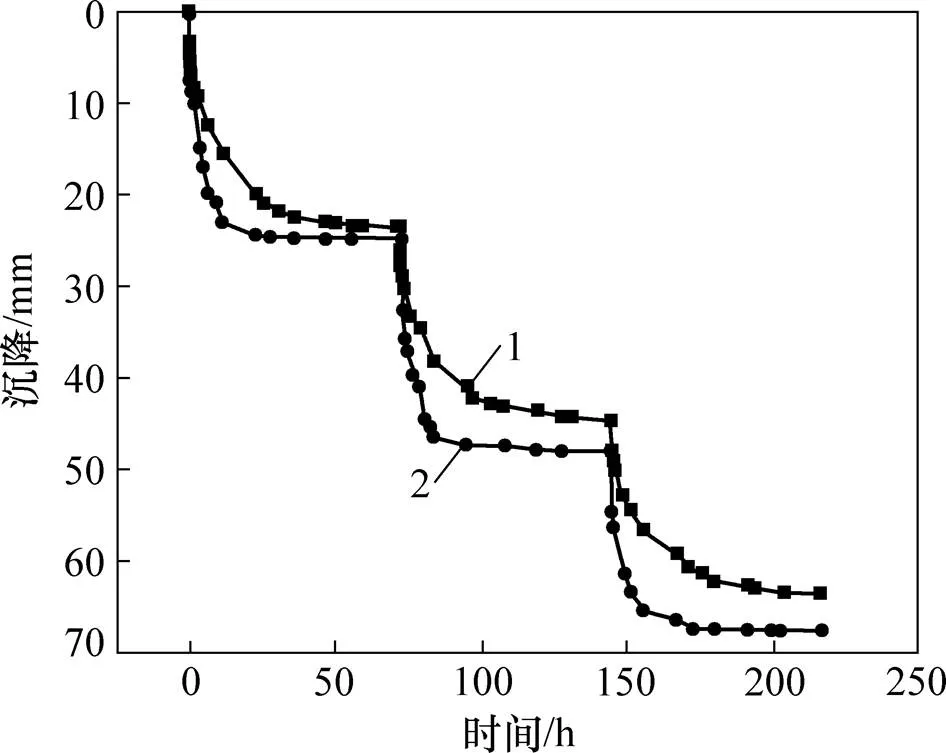
1—排水固结；2—热排水固结。

2.4 固结度

地基固结度可按变形或孔隙水压力定义，但由于残余孔压影响，按沉降来定义模型试验地基的固结度则更为合理，结果如图8所示。在各级堆载压力下，热排水固结模型试验的固结度增长较排水固结快，即到达同一固结度所用的时间减少，取固结度为90%时，每级堆载作用下热排水固结模型试验所用时间平均值较排水固结试验减少了约58.6%。这也验证了文献[1]和[4]中的结论，即对土样进行加热可提高其渗透系数，加速土样的排水固结。对于工程条件下的地基情况，需要通过原位试验验证。

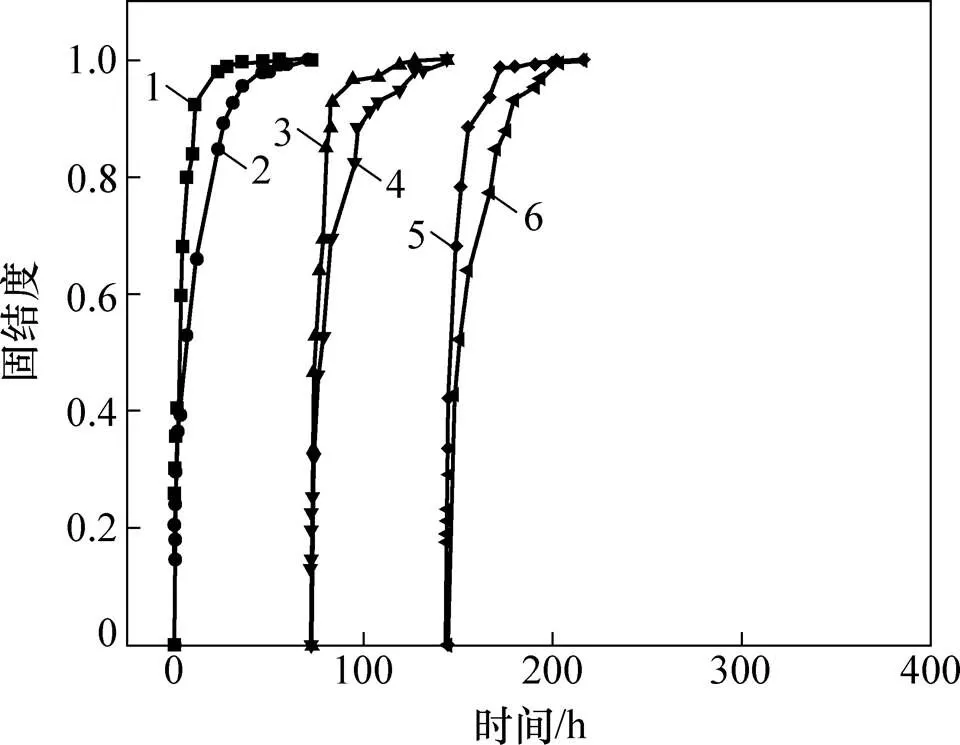
1—热排水固结，第1级堆载；2—排水固结，第1级堆载；3—热排水固结，第2级堆载；4—排水固结，第2级堆载；5—热排水固结，第3级堆载；5—排水固结，第3级堆载。

2.5 土的强度

在每次模型试验完成后，取模型顶部同一位置土体进行固结不排水剪切试验，试样在75 kPa的轴压和围压下进行等压固结，待固结完成后进行不排水剪切试验，结果如图9所示。由图9可以看出：热排水固结模型试验土体经过温度历史后，其剪切强度较排水固结模型试验土的强度有所提高，取应变为20%时，其强度提高了22.7%。

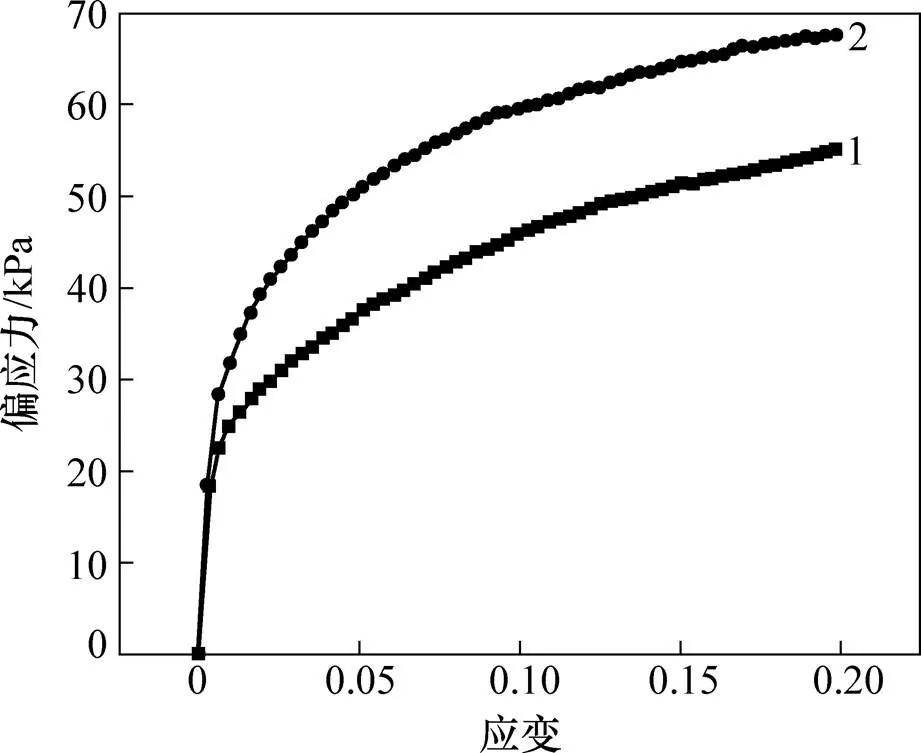
1—排水固结；2—热排水固结。

3 考虑温度影响的沉降计算

基于不同温度下同一土体压缩或回弹线斜率不变[17]，考虑土体先期固结压力随温度变化情况，以土体−lg曲线上点在温度或堆载作用下的移动规律来分析热排水固结模型试验各阶段的沉降变化，并对模型试验地表沉降进行简化计算。

3.1 先期固结压力变化对沉降的影响

土体加热时，因孔隙水热膨胀系数较土颗粒大，导致二者膨胀速率不一致，土骨架限制孔隙水膨胀，导致孔隙水压力增大，随着土体温度的升高，土体温度变化放缓，孔压增长速率减小。又孔隙水黏滞系数随土体温度的升高而减小，土体渗透性增大，固结过程加快，孔压最终消散至稳定。

仅从土体成分热膨胀特性的差异来分析土体沉降是不够完善的，因为孔隙水与土颗粒都受热膨胀，土体应表现为膨胀，但现有文献表明：在荷载作用下弱固结土与正常固结土加热排水固结体变是压缩[6, 8, 18]。本次模型试验在无堆载加热阶段(此时荷载是自重)，土体表面最终表现也为沉降，验证了相关结论，这一现象产生的主要原因就是土体先期固结压力随温度变化而变化。为此，本节结合温度对土体先期固结压力的影响规律，进行分析对固结沉降的影响。

3.1.1 无堆载加热阶段

图10所示为考虑先期固结压力随温度变化的−lg曲线。如图10所示，假定土体初始先期固结压力为3，初始有效应力为1，初始孔隙比为1，初始温度为，当温度由升高至1。土体先期固结压力由3减小至2，−lg曲线1上的点将移动至−lg曲线2上点，并沿−lg曲线2的回弹线重新固结至点，在此过程中，有效应力先减小后增大，则孔压应先增大后减小，土体孔隙比由1减小至2，土体最终表现为沉降。

在此过程有3个部分位移：第1部分是加温引起的膨胀；第2部分是有效应力先减小后增加产生的土体表面先回弹后压缩，如果温度引起的超静孔压消散，该部分引起的位移为0；第3部分就是由于加热引起先期固结压力减小产生的沉降。温度快速增加阶段，有效应力减少引起的膨胀与热胀引起的膨胀比先期固结压力减小产生的沉降大，所以位移表现为膨胀。在孔压消散后，最终位移将由第1部分与第3部分产生，很明显第3部分产生的沉降大于由第1部分产生的膨胀，所以最终位移表现为沉降。

3.1.2 分级堆载阶段

土体温度的升高一方面减小孔隙水粘滞系数，使土体渗透性增大，另一方面减小土颗粒间结合水膜厚度，增大孔隙水排水通道，使土体渗透性进一步增大[1]，从而减少了热排水固结模型试验恒温堆载阶段的固结时间。

分级堆载阶段，土体热膨胀现象不复存在，土体沉降应结合图10进行分析，如图9所示，土体温度恒定为1，堆载作用下土体有效应力由1增长到4，−lg曲线2上的点移动至点，土体孔隙比由2减小至4。若不进行加热，相应的−lg曲线1上的点将移动至点，孔隙比减少量应为3−1，又−lg曲线上压缩线的斜率较回弹线大，故(4−2)＞(3−1)，即堆载作用下热排水固结模型试验地表沉降较排水固结模型试验增大。

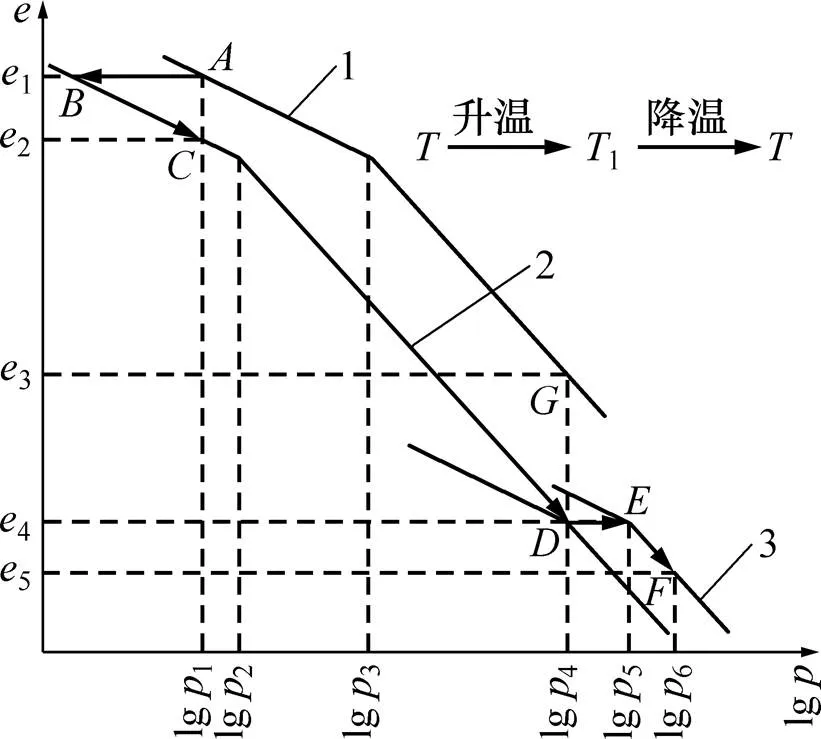
图10 考虑先期固结压力随温度变化的e−lg p曲线

3.1.3 恒载降温阶段

土体降温时，因孔隙水热膨胀系数较土颗粒大，导致二者收缩速率不一致，土骨架限制孔隙水收缩，导致土体残余孔压减小至负值，孔压表现为吸力，土体产生吸水现象，随着孔隙水回吸，孔压逐渐增长至稳定。

土体降温时，孔隙水与土颗粒均收缩，土体表现为收缩。另一方面，由图10可见：当温度由1降低至，土体的先期固结压力由4增大至5，−lg曲线2上的点移动至−lg曲线3上的点，又土体降温导致残余孔压减小，有效应力增大，当降温引起的有效应力增大值(6−4)大于先期固结压力增大值(5−4)时，土体将沿−lg曲线3的压缩线固结至点，土体孔隙比由4减小至5，土体表现为沉降。

上述过程在热排水固结模型试验恒载降温阶段应同时发生，该阶段土体沉降应为上述过程的综合作用效果。

3.2 简化计算

模型试验中宁波软黏土的试验参数如表1所示。

表1 模型试验参数

由于土体与模型桶内壁的摩擦及残余孔压存在，将堆载直接全部转化为有效应力，其计算不合理。应将堆载进行适当的折减，定义，为堆载折减系数，f为堆载压力，Δ堆载引起的有效应力增量。由于从理论上给出折减系数相当困难，只能从一次试验结果反演计算出该折减系数，并假设各次试验中土样与模型筒壁折减系数不变，则可以通过第二次试验结果验证这个折减系数。本次模型试验，由常规排水固结试验结果反演计算得到了折减系数为0.45，并由热排水固结试验验证了该折减系数的合理性。

对于固结沉降问题，按−lg曲线法求解土体沉降的计算公式简单、适用，其表达式为[19]

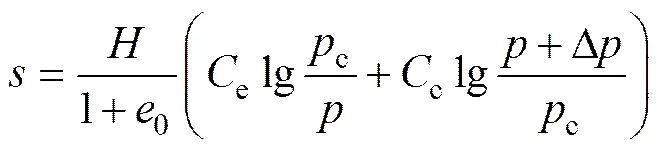
式中：为沉降；为土层厚度；0为初始孔隙比；e为回弹指数；c为压缩指数；c为先期固结压力，为初始有效应力；Δ为有效应力增量。

对于热排水固结问题，由于温度场的影响，不能再按式(1)进行沉降计算，而建立一套新的计算理论难度较大。为此，在−lg曲线法基础上，尝试建立热排水固结沉降的简化计算，以预测不同温度下热排水固结地基的沉降。LALOUI等[18]认为先期固结压力的改变量与土体温度变化之间满足下述关系：

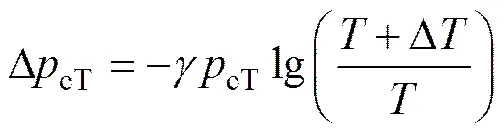
式中：ΔcT为先期固结压力的改变量；为先期固结压力温度影响参数，LALOUI等[18]建议取=0.3~0.4；cT为温度时土体的先期固结压力；Δ为温度变化值。

因此，本文忽略热胀冷缩对沉降的影响，即不考虑温度对，0，e和c的影响，仅考虑温度对先期固结压力的影响，利用式(1)和(2)，建立考虑温度影响的土体沉降计算理论，扩展了−lg曲线法的应用 范围。

3.2.1 无堆载加热阶段

该阶段地表沉降由土体先期固结压力受温度作用减小引起。沉降计算公式为

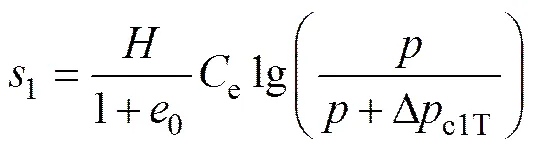
式中：Δc1T为加热引起的先期固结压力c1变化量，c1为土体加热前的先期固结压力。

3.2.2 分级堆载阶段

该阶段地表沉降因堆载引起。沉降计算公式为

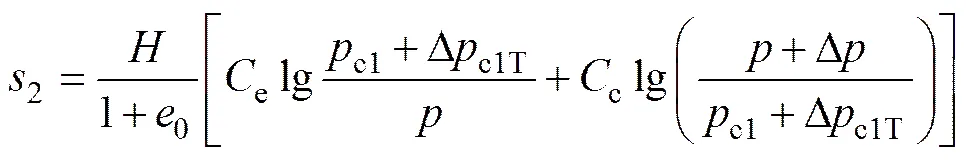
式中：Δ为堆载引起的有效应力增量。

排水固结模型试验仅有分级堆载过程，其地表沉降计算式取式(4)的退化情况，即Δc1T= 0。

3.2.3 恒载降温阶段

该阶段先期固结压力虽受温度作用增大，但降温也导致孔隙水压力减小，地表沉降为二者综合作用的结果。沉降计算公式为

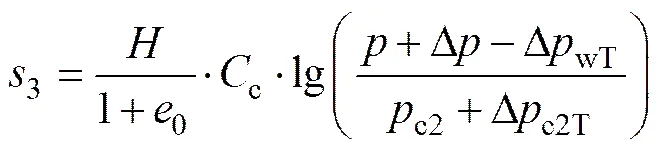
式中：ΔwT为孔隙水压力因温度降低的变化量；c2为堆载后土体的先期固结压力；Δc2T为降温引起的先期固结压力c2的变化量。

利用表1所示的模型试验参数，进行地表沉降计算，结果如表2所示。由表2可以看出：排水固结模型试验累计沉降计算结果与实测结果接近，而所建立的热排水固结沉降简化计算结果也与实测结果较为一致。尽管，热排水固结沉降−lg曲线简化计算仅是在现有理论基础上进行简单扩展，但通过试验结果和计算结果的比较，初步验证该方法是合理的，但其可靠性尚有待进一步研究。

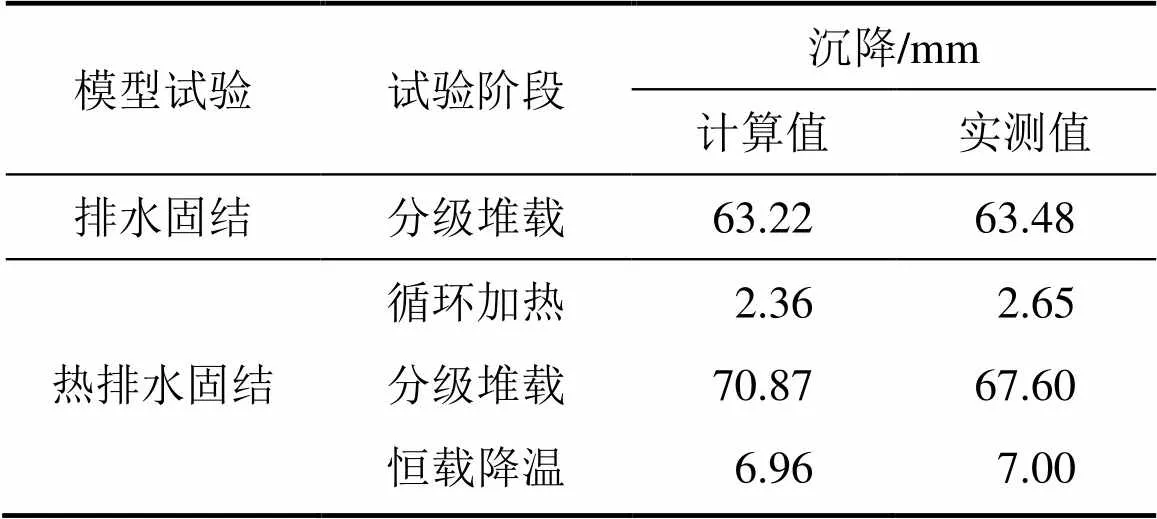
表2 模型试验地表沉降计算值与实测值

4 结论

1) 按沉降定义的固结度达到90%时，水热循环温度70 ℃的热排水固结所用时间较排水固结减少58.6%。从模型试验结果初步推断热排水固结可有效缩短软基处理周期。

2) 温度变化可改变土体的先期固结压力，水热循环温度为70 ℃时，热排水固结法模型地表沉降量较排水固结法增加21.7%。

3) 在恒载降温段，降温能使残余孔压快速消散，土体有效应力增加，土体沉降继续增大。

4) 由于热排水固结过程中排出水量、沉降的增加，处理后的土体孔隙较排水固结法小，密实度增加，土的抗剪强度提高22.7%。

5) 基于−lg曲线法建立的热排水固结沉降的简化计算结果与实测结果较为吻合，该方法是合理的，但其可靠性尚有待进一步研究确定。

[1] POTHIRAKSANON C, DENNES T B, ABUEL-NAGA H M. Full-scale embankment consolidation test using prefabricated vertical thermal drains[J]. Soils and Foundations, 2010, 50(5): 599−608.

[2] TIDFORS M, SALLFORS G. Temperature effect on preconsolidation pressure[J]. Geotechnical Testing Journal, 1989, 12(1): 93−97.

[3] BOUDALI M, LEROUEIL S, SRINVIASA MURTHY B R. Viscous behavior of natural clays[C]//Proceedings of 13th International Conference on Soil Mechanics and Foundation Engineering. New Delhi, 1994: 411−416.

[4] TOWHATA I, KUNTIWATTANAKU P, SEKO I, et al. Volume change of clays induced by heating as observed in consolidation tests[J]. Soils and Foundations, 1993, 33(4): 170−183.

[5] SULTAN N, DELAGE P, CUI Y J. Temperature effects on the volume change behaviour of Boon clay[J]. Engineering Geology, 2002, 64: 135−145.

[6] ABUEL-NAGA H M, DENNES T B, BOUAZZA A. Thermally induced volume change and excess pore water pressure of soft Bangkok clay[J]. Engineering Geology, 2007, 89: 144−154.

[7] ROMERO E, GENS A, LLORET A. Temperature effects on the hydraulic behavior of an unsaturated clay[J]. Geotechnical and Geological Engineering, 2001, 19(3/4): 311−332.

[8] TSUTSUMIA A, TANAKAB H. Combined effects of strain rate and temperature on consolidation behavior of clayey soils[J]. Soils and Foundations, 2012, 52(2): 207−215.

[9] 吴瑞潜. 饱和土一维热固结解析理论研究[D]. 杭州: 浙江大学, 2008. WU Ruiqian. Analytical study on one-dimensional thermal consolidation theory of saturated soil[D]. Hangzhou:Zhengjiang University, 2008.

[10] 白冰. 无限长圆柱饱和多孔热弹性介质的固结解[J]. 岩土工程学报, 2010, 32(11): 1665−1670. BAI Bing. Consolidation solutions of a saturated porothermoelastic cylinder with infinit length[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1665−1670.

[11] 陶海冰, 谢康和, 刘干斌, 等. 考虑温度耦合效应的竖井地基固结有限元分析[J]. 岩土力学, 2013, 34(S1): 494−500. TAO Haibing, XIE Kanghe, LIU Ganbin, et al. Finite element analysis of consolidation by vertical drains coupled thermo-hydro-mechanical effect[J]. Rock and Soil Mechanics, 2013, 34(S1): 494−500.

[12] 王安明, 李小根, 李彰明, 等. 软土动力排水固结的室内模型试验研究[J]. 岩土力学, 2009, 30(6): 1643−1648. WANG Anming, LI Xiaogen, LI Zhangming, et al. Indoor model test of dynamic drainage consolidation method of soft soil[J]. Rock and Soil Mechanics, 2009, 30(6): 1643−1648.

[13] 王柳江, 刘斯宏, 汪俊波, 等. 真空预压联合电渗法处理高含水率软土模型试验[J]. 河海大学学报(自然科学版), 2011, 39(6): 671−675. WANG Liujiang, LIU Sihong, WANG Junbo, et al. Model test for high-water-content soft soil treatment under vacuum preloading in combination with electroosmosis[J]. Journal of Hohai University (Natural Sciences), 2011, 39(6): 671−675.

[14] 闫澍旺, 孙立强, 李伟, 等. 真空加固超软土工艺的室内模型试验研究[J]. 岩土工程学报, 2011, 33(3): 341−347. YAN Shuwang, SUN Liqiang, LI Wei, et al. Model test on vacuum preloading technology of super-soft soil[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3): 341−347.

[15] 余飞, 王小刚, 陈善雄, 等. 软土电化学桩加固室内模型试验研究[J]. 岩石力学与工程学报, 2013, 32(S1): 2716−2722. YU Fei, WANG Xiaogang, CHEN Shanxiong, et al. Laboratory model test study of electrochemical stabilization in soft soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2716−2722.

[16] 邓岳保, 谢康和, 李传勋. 考虑非达西渗流的比奥固结有限元分析[J]. 岩土工程学报, 2012, 34(11): 2058−2065. DENG Yuebao, XIE Kanghe, LI Chuanxun. Finite element analysis of Biot’s consolidation with non-Darcianflow[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2058−2065.

[17] CUI Y J, SULTAN N, DELAGE P. A thermomechanical model for saturated clays[J]. Canadian Geotechnical Journal, 2000, 37(3): 607−620.

[18] LALOUI L, CEKEREVAC C. Thermo-plasticity of clays: an isotropic yield mechanism[J]. Comput Geotech, 2003, 30(8): 649−660.

[19] 李广信. 高等土力学[M]. 北京: 清华大学出版社, 2004. LI Guangxin. Advanced soil mechanics[M]. Beijing: Tsinghua University Press, 2004.

(编辑 陈爱华)

Model test on thermal drainage consolidation of foundation with vertical drain

LIU Ganbin1, FAN Gaofei1, TAO Haibing1, 2, YIN Tiefeng1, DENG Yuebao1

(1. Institute of Geotechnical Engineering, Ningbo University, Ningbo 315211, China;2. Research Center of Coastal and Geotechnical Engineering, Zhejiang University, Hangzhou 310027, China)

Model test system was designed for thermal shaft drainage consolidation, and then tests of thermal drainage consolidation and drainage consolidation were carried out by selecting typical soft clay of Ningbo area at room temperature and the hydrothermal fluid circulation temperature of 70 ℃, respectively. The change law of temperature and pore water pressure of each measuring points and ground surface settlement were analyzed for the heating, step loading and cooling (constant load) stage, and the mechanism of thermal drainage consolidation was preliminary elaborated. The results show that the thermal drainage consolidation method can accelerate the consolidation rate of the ground model, and consolidation time required to achieve 90% reduction compared with the drainage consolidation method significantly. After the temperature history, the final settlement of the surface, shear strength increase, and the soft ground treatment effect is enhanced.On this basis of tests, combined with the existing preconsolidation pressure varies with temperature theory, the formula for calculating the subsidence of thermal drainage consolidation method is developed according to−lgcurve, and theoretical calculations of the ground surface settlement of the shaft foundation are in good agreement with the experimental results, which initially verifies the reasonableness of settlement calculation formula.

thermal drainage consolidation; model test; shaft foundation;−lgcurve; settlement

10.11817/j.issn.1672−7207.2017.02.024

TU447

A

1672−7207(2017)02−0448−09

2016−04−16；

2016−06−22

国家自然科学基金资助项目(51278256, 51478228)(Projects(51278256, 51478228) supported by the National Natural Science Foundation of China)

刘干斌，博士，教授，从事多物理场土力学和土动力学方面研究；E-mail：Liugb76@163.com