基于改进的BP神经网络的水面蒸发预测

李 俊(太原理工大学水利科学与工程学院，太原 030024)

水面蒸发作为水循环的一个重要环节，对水资源的合理开发、制定适当的灌溉制度起到十分重要的影响[1]，因此对水面蒸发量进行预测能够为农业活动的决策提供一定的依据。

现行预测水面蒸发量的方法有：多元线性回归模型[2]、灰色预测模型[3]、RBF神经网络模型[4]、BP神经网络模型[5]等，水面蒸发量与各个因素之间存在着复杂的线性关系，所以使用多元线性回归模型并不能很好地反映水面蒸发的这一特性，而灰色预测模型存在对背景值和初始值的规定是不尽合理的缺点[6]，为了达到相同的精度要求，RBF神经网络的实现结构复杂过BP神经网络的，因此针对水面蒸发与预测因素之间存在非线性关系的特点，以及模型的简洁性，本文使用BP神经网络来对水面蒸发进行预测，同时为了改变以往使用BP神经网络预测水面蒸发的过程中没有对指标进行筛选，造成模型结构不必要的扩展，降低模型工作效率，因此本文使用灰色关联理论对指标进行初步筛选，去除一些与水面蒸发相关性相对较弱的指标，从而减少预测模型的输入，优化网络结构。以往使用灰色关系法进行指标筛选时，只是主观的确定一个关联度阀值来对指标进行筛选，但并未对筛选后指标的合理性进行分析[7]，存在很大的主观性，因此本文使用方差来代表指标的信息[8]，对海选指标与筛选后的指标的信息进行比较，从而得出筛选后的指标的信息持有度(简称此法为指标信息评价法)，以此来对指标的合理性进行分析。

本文称结合灰色关联法、指标信息评价法与BP神经网络的方法为改进的BP神经网络法，以太原地区的水面蒸发预测为例进行预测演算，并对预测模型的合理性进行分析，以期验证预测模型的合理性，为水面蒸发的预测提供参考。

1 模型介绍

按照上文的内容，本文按照灰色关联法、指标信息评价法与BP神经网络3个部分来对改进的BP神经网络模型进行介绍。

1.1 灰色关联法

灰色关联度可以表示2个指标之间的密切程度[9]，因此计算各个预测因子与被预测因子之间的关联度，从而得出各个预测因子与被预测因子的密切程度。

设有n-1个预测因子，1个预测因子，共有m组数据，得到以下矩阵样本：

(1)

式中：xi，j为第i组的第j个指标值(1≤j≤n-1)；xi，n为第i组的预测值。

对预测因子与被预测因子标准化，以避免指标量纲的影响，按下式计算：

(2)

式中：yij为标准化后的指标值。

使用式(2)对式(1)中的每一个指标值进行标准化转换后，可以得到以下矩阵：

(3)

通过式(4)求每一个预测因子与被预测因子对应预测因子的关联度。

(4)

式中：k(ij)为预测因子yij与被预测因子yin对应指标的关联度；λ一般取0.5。

接着使用式(5)求每个预测因子与被预测指标的关联度。

(5)

根据各个预测因子的关联度来进行排序(联系度越大，联系越密切)。

1.2 指标信息评价法

变异系数法中提出使用方差大小来表示指标携带信息的多少，从而对指标进行赋权[10]。同样的，可以使用方差的大小来评定筛选后的指标是否发生信息丢失，从而对指标的合理性进行评价。具体方法如下。

根据式(5)计算得到的每个指标与被预测指标的关联度，从高到低对各个预测因子进行排列，从而得到以下样本矩阵[按照关联度高低把矩阵式(3)前n-1列从左到右排列，最后一列为被预测因子与矩阵式(3)最后一列相同]。

(6)

式中：za，b为第a组的第b个指标值(1≤a≤n-1)；yi，n为第i组的预测值。

使用预测因子的信息持有度Rb来表示筛选出的b个预测因子所持有的信息占原预测因子信息的百分比，由此叙述可得以下公式。

Rb=(Sb/Sn-1)×100%

(7)

式中：Sb与Sn-1与分别为矩阵式(6)中前b个预测因子的方差、矩阵式(6)中前n-1个预测因子的方差。

不断地对b进行取值进行试算，当Rb大于M时，对应最小的b即是最优预测因子个数，前b个预测因子为最优预测因子。在主成分分析理论中，通常保留累计方差贡献率达到70%～90% 的信息含量较大的主成分，表示全部原始指标信息的绝大多数得到了反映[11]，借助此思想，且为保险起见，M取90%。

1.3 BP神经网络

BP神经网络是一种按误差逆传播算法训练的多层前馈网络[12]。同时其能够反映被预测因子与预测因子之间的非线性关系，适合用于水面蒸发预测。

BP神经网络的工作示意图见图1。从左到右的三列圆圈分别表示输入层、隐含层、输出层，分别说明如下。

图1 BP神经网络工作示意图Fig.1 Schematic diagram of BP neural network

输入层：在本文中输入层一般为预测因子，输入层节点的个数也和最优预测因子个数相等。

隐含层：对以隐含层的节点数目前没有统一的确定方法，一般取为输入层节点数的75%[13]，按照这个比例选取几个可能的节点数进行试验，最终确定最优隐含层的节点数。

输出层：输出层节点的个数和被预测因子个数相等，在本文中等于1。

在确定以上结构后，编写程序，在Matlab R2013a中进行运算。

1.4 改进的BP神经网络模型

综合以上3部分，对改进的BP神经网络模型的演算流程进行介绍，具体如下。

(1)使用灰色关联法分别计算各个海选预测因子与被预测因子的关联度，并按照关联度大小从左到右对海选预测因子进行排列。

(2)使用指标信息评价法判定出最优预测因子组合。

(3)根据最优预测因子组合、BP神经网络的结构特点与水面蒸发预测的特点定出BP神经网络的结构，使用Matlab R2013a编程实现BP神经网络算法。

(4)对结果进行合理性分析。

2 实例演示

本文选取太原地区为研究区域，收集2008年10月1日至2009年4月30日的逐日的平均气压、日最高气压、日最低气压、日最高气温、平均风速、最大风速、极大风速、日照时数、蒸发量作为基础资料，其中选取平均气压、日最高气压、日最低气压、日最高气温、平均风速、最大风速、极大风速、日照时数为海选预测因子，蒸发量作为被预测因子。

由以上说明可知，在矩阵式(1)、式(3)、式(6)中m和n的取值分别为212、9。同时选择2008-10-01-2009-03-31的数据作为训练指标，而2009-04-01-2009-04-30的数据作为检验指标。具体数据见表1(应该展示的数据为2008年10月至2009年4月7个月的数据，但限于篇幅只是展示了2008年10月这一整个月的数据)。

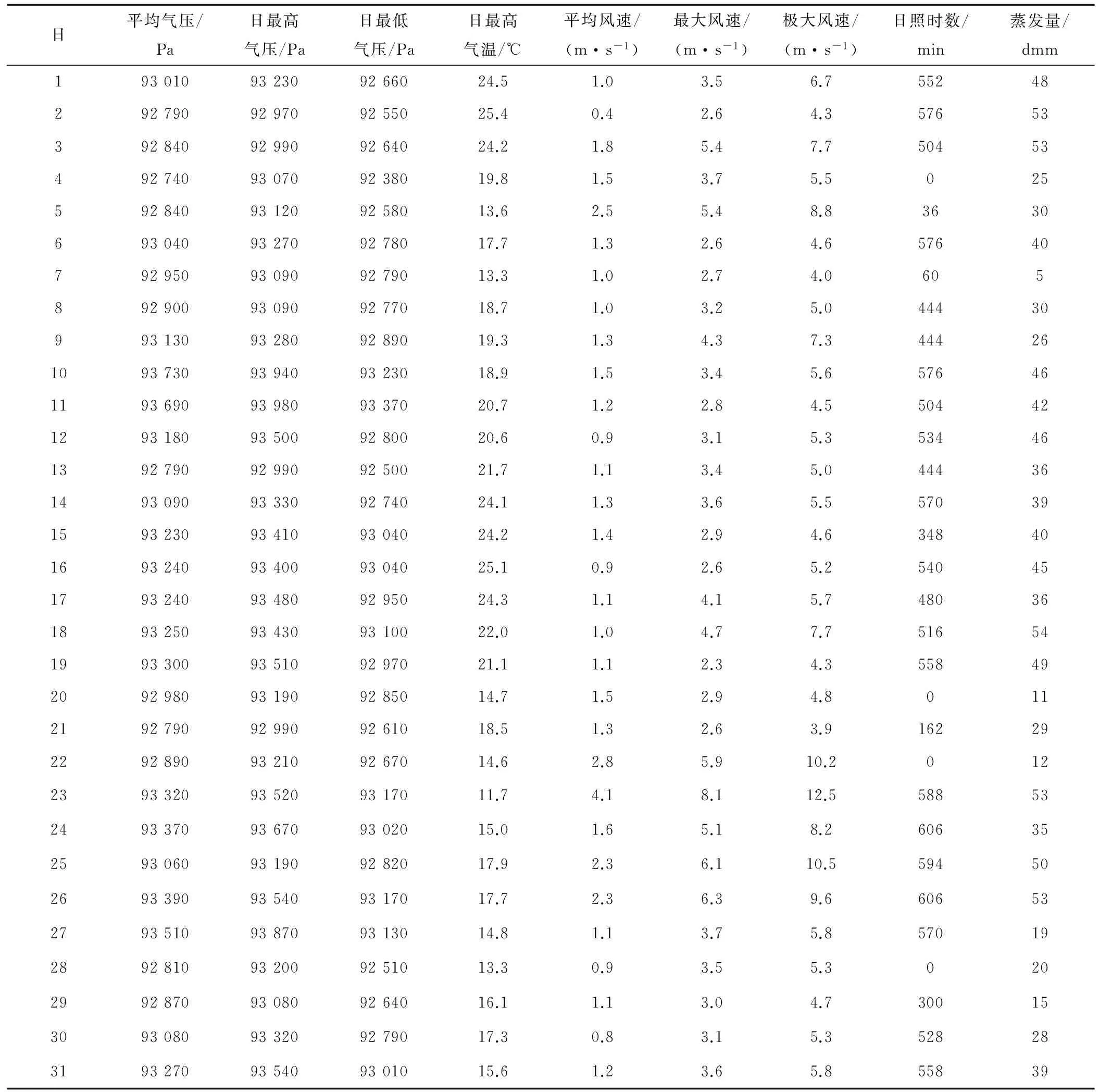
表1 示例数据表(2008年10月)Tab.1 Sample data sheet(2008.10)

注：表1中,使用了国际单位的表示方法，但在后文的计算中为了和收集的数据一致，所以后文的数据依然以使用原数据的单位表示，即平均气压、日最高气压、日最低气压、日最高气温、平均风速、最大风速、极大风速、日照时数、蒸发量的单位分别为：0.1 hPa、0.1 hPa、0.1 hPa、0.1 ℃、0.1 m/s、0.1 m/s、0.1 m/s、0.1 h、0.1 mm。

根据式(2)对表1的数据进行标准化，使用式(4)和式(5)计算各个预测因子与被预测因子的关联度，结果见表2。

选取不同的b值带入公式(7)进行试算，各个b值对应的信息持有度见表3。

表2 预测因子关联度表Tab.2 Predictive factor correlation degree

表3 b值与Rb对应关系表Tab.3 Relationship between b and Rb

由表3可知Rb大于90%时，最小的b值为5，故最优预测因子为日最高气温、日照时数、极大风速、平均风速、最大风速。

由以上可得，在BP神经网络中输入层的节点数为5，经过对可能隐含层节点数的试验，得出隐含层节点数为4，输出层节点数为1，所以BP神经网络的结构为5-4-1。

以日最高气温、日照时数、极大风速、平均风速、最大风速为预测因子，蒸发量为被预测因子。

同时选择2008-10-01-2009-03-31的数据作为训练指标，而2009-04-01-2009-04-30的数据作为检验指标。使用Matlab R2013a编程实现模型算法。检验结果见表4。

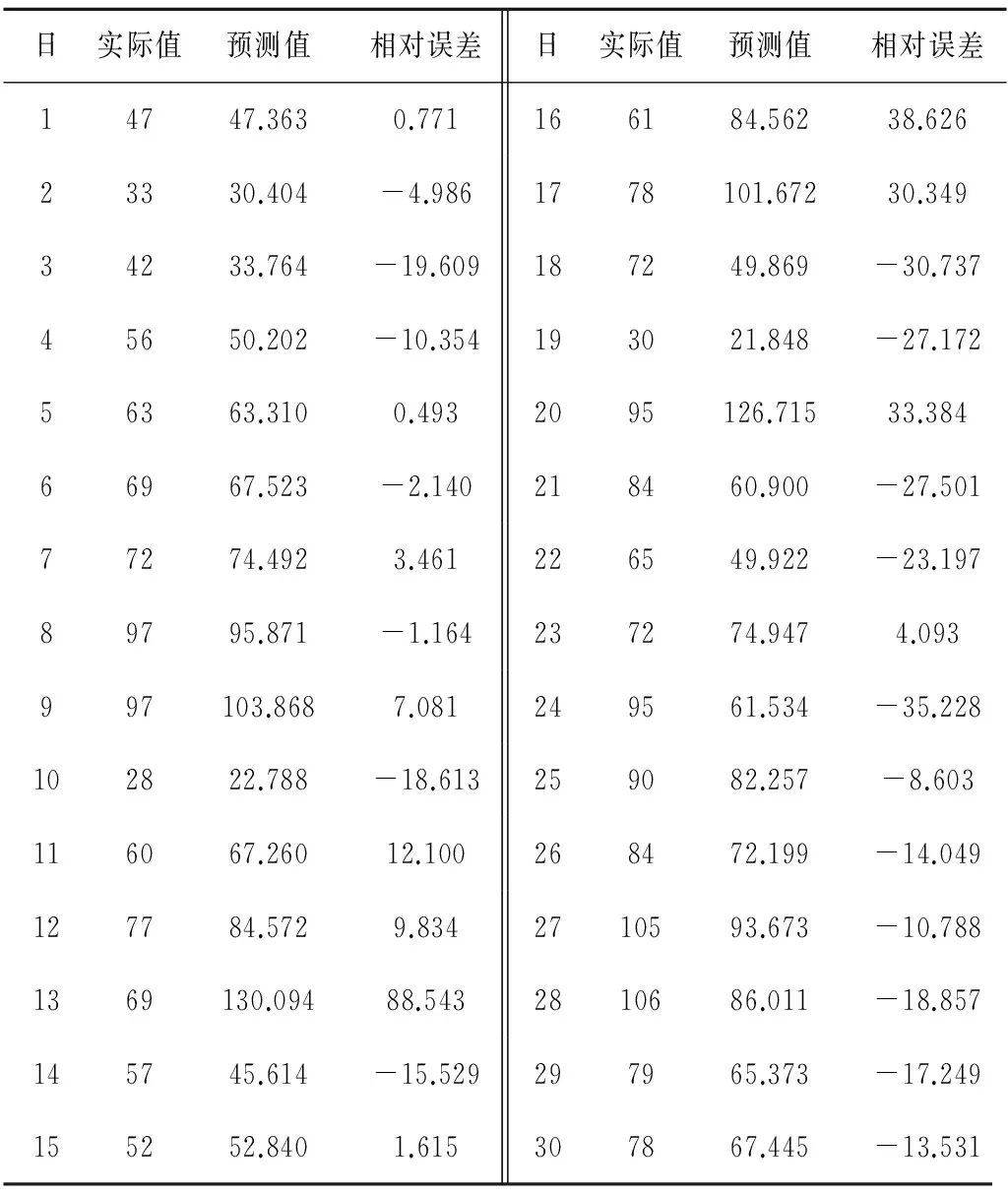
表4 检查结果表(2009年4月)Tab.4 Result of checking(2009-04)

如果相对误差绝对值小于20%算作合格的话[2]，合格率等于(21/30)×100%=70%。

3 结 语

本文以太原地区的水面蒸发预测为例，使用结合灰色关联法、指标信息评价法与BP神经网络法的改进的BP神经网络法对该研究区的水面蒸发进行预测，最后得出该模型的预报的合格率为70%。

灰色关联法可以计算各个预测因子与被预测因子的关联度，可以为指标的筛选作准备，同时使用指标信息评价法可以避免人为主观确定关联度阈值来选定最优最优预测因子的缺点，通过灰色关联法与指标信息评价法来对指标进行筛选，可以减少BP神经网络的输入节点，优化BP神经网络的结构，提高预测效率。

综上可以得出该模型对于水面蒸发的预测具有一定适用性。

[1] 徐继红.干旱区影响水面蒸发的气象因素多元回归分析[J].水利规划与设计,2016,(9)：62-64.

[2] 魏光辉,董新光,杨鹏年,等.基于灰色关联分析与多元线性回归模型的水面蒸发预测[J].节水灌溉,2012,(2)：41-44.

[3] 石丽忠,陈金良,迟道才,等.关于辽阳市水面蒸发量灰色预测模型的研究[J].节水灌溉,2007,(8)：37-39.

[4] 魏光辉,马 亮.基于灰色关联分析与RBF神经网络的水面蒸发量预测[J].干旱气象,2009,27(1)：73-77.

[5] 刘彩红,冯宗友.基于BP神经网络的新疆平原地区水面蒸发量预测模型研究[J].重庆工学院学报(自然科学版),2007,21 (6)：87-89.

[6] 杨华龙,刘金霞,郑 斌.灰色预测GM(1,1)模型的改进及应用[J].数学的实践与认识,2011,41 (23)：39-46.

[7] 薛 楠,邬贻萍,郐 晶.灰色关联度在单病种质控指标筛选中的应用[J].中国卫生统计,1999,16 (3)：181-182.

[8] 顾在浜,石宝峰,迟国泰.基于聚类—灰色关联分析的绿色产业评价指标体系构建[J].资源开发与市场,2013,29(4)：350-354.

[9] 刘 博,肖长来,田浩然,等.灰色关联和层次分析法在地下水质评价中的应用----以吉林市为例[J].节水灌溉,2013,(1)：26-29.

[10] 张小泓. 基于变异系数法的灰色关联模型在节水灌溉工程投标方案优选中的应用[J].节水灌溉,2009,(8)：54-56.

[11] 汪冬华.多元统计分析与SPSS 应用[M]．上海：华东理工大学出版社，2010:192-215.

[12] 于 涛. BP网络自适应学习率算法分析[D].大连：大连理工大学，2011：1-2.

[13] 唐启义,冯明光. DPS数据处理系统[M]．北京：科学出版社，2006:933-934.