破碎花岗岩非达西渗流的试验研究

贺香兰，周佳庆，魏 凯，王 敏

(1.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 武汉大学水工岩石力学教育部重点实验室，武汉 430072)

0 引 言

裂隙是岩体渗流的主要通道，控制着岩体的渗流特性，随着高坝枢纽工程和抽水蓄能电站的兴建，岩体可能承受高渗压、高水力梯度作用，此时节理裂隙等结构面易张开扩展，甚至发生水力劈裂，岩体渗流往往表现出非达西特征，特别是对于裂隙充分发育的破碎岩体，渗流特性更为复杂。黄先伍等[1]、李顺才等[2]在破碎岩石构成的多孔介质渗流试验的基础上，研究了非达西渗流特性与孔隙率的关系；Thauvin和Mohanty[3]利用数值模拟的方法从细观结构的角度研究了多孔介质非达西渗流的成因；胡大伟等[4]研究了单轴压缩破坏的大理岩峰后非线性渗流特征演化规律。

对于非达西流，传统的达西渗流理论已不能准确表征岩体的渗透特性，因此渗流流态的判断和分析理论的选择是研究介质渗流的关键。为此，国内外学者对达西流与非达西流的临界条件开展了大量研究，主要采用雷诺数Re和福希海默数F0作为临界参数[5]。孟如真等[6]、李健等[7]分别通过现场压水试验和室内渗流试验，得到了量级为10～100的临界雷诺数；Zimmerman等[8]通过对单裂隙砂岩进行渗流试验和数值模拟，发现Re大于20时，渗流满足Forchheimer非达西方程；Javadi等[9]开展了粗糙裂隙面渗流试验，得到的临界雷诺数介于0.001～25；同时还有文献提出了高达2 300的临界雷诺数[10]。另一方面，Zeng和Grigg等[11]根据福希海默数F0的定义及其物理意义，建议取F0=0.11作为达西流和非达西流的临界值；随后，Macini等[12]通过研究天然砂粒的渗流试验，得到值为0.4左右的临界福希海默数，该值对应28%的非达西效应；文献[13]在进行数值模拟时采用了F0=0.01作为临界值。通过众多研究可以发现，雷诺数Re和福希海默数F0临界值的取值范围变化较大，且目前尚未得到临界值的变化规律，因此采用参数Re和F0判断渗流流态存在一定的主观性和不确定性。

综上所述，尽管渗流的非达西性得到了大量的研究，但涉及破碎岩体的非达西渗流的研究成果相对较少，并且达西流和非达西流的临界问题仍未得到有效地解决。基于此，本文通过开展破碎花岗岩在不同围压条件下的高水力梯度非达西渗流试验，研究破碎岩体复杂裂隙介质的渗流特性，并在试验结果基础上，提出一种简单直观方便的非达西流判定方法。该方法可将临界值的不确定性问题转化为实际工程目标需求的容许误差，具有较好的实用价值。

1 试验系统与步骤

1.1 试验系统介绍

破碎岩体非达西渗流试验在武汉大学与法国里尔科技大学(USTL)联合研发的Triaxial Cell三轴试验系统上进行，见图1。该系统由围压、轴压和孔隙水压3套独立加载部分构成，具有应力、应变、位移和流量4种控制加载方式，可施加最大围压60 MPa，最大轴压375 MPa，最大渗透水压力50 MPa。其中渗透水压力由升级后的高精度液压泵PHMP 50-1000型施加，该流量泵可容纳100 mL体积水，流量范围为0.000 41～66.8 mL/min。系统出口端接入测量精度为0.01 g的SA2202S-CW 型高精度自动电子天平，以测量出口水流流量。

1.2 试验步骤

试验岩样取自广东省阳江抽水蓄能电站高压隧洞区，为中粒花岗岩，经取芯机、刚性切割机和打磨机加工后制备得到Φ50 mm×100 mm的圆柱状标准岩石试样，见图2。破碎岩体渗流试验过程如下。

(1)将饱和的标准岩石试样在预定围压条件下施加轴向压力，直至试样破坏，得到破碎岩样。

(2)以位移加载模式控制岩样保持在破碎初始状态，并以0.1 MPa的渗透水压持续进行12 h的过流，保证试样充分饱和。

(3)在设定的围压条件下，逐级施加渗透水压(见图3)，测量并记录每级水压稳定后的出口水流流量，完成该围压下的渗流试验后，改变围压，重复上述过程，直至围压达到30 MPa。

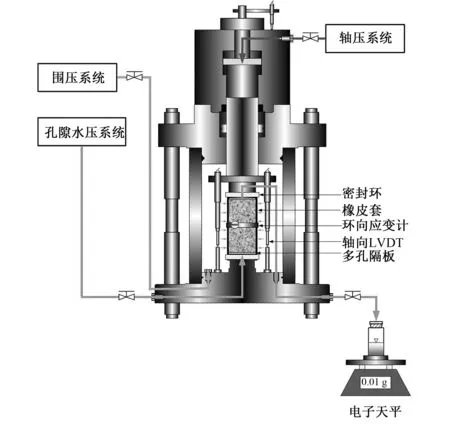
图1 非达西渗流试验装置Fig.1 Sketch of non-Darcy flow test equipment

图2 试验前后花岗岩试样Fig.2 Granite samples before and after test

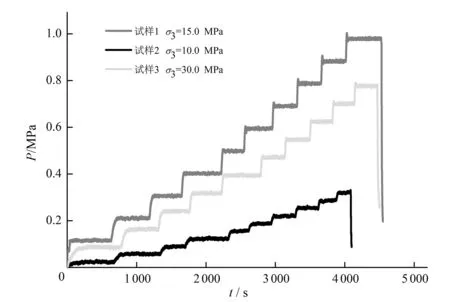
图3 渗透水压加载过程曲线Fig.3 Curves of the applied water pressure

2 试验结果与分析

试验采用阳江破碎花岗岩标准岩样，每个试样开展了不少于10级围压下的不同水力梯度的渗流试验。试验后的3个破碎岩样见图2(b)。由图2(b)可见，试样破碎程度较高，纵向裂隙发育，部分贯通试样，同时存在少量横向裂纹。本文给出了试样1～3岩石试样在不同围压条件下两端水力梯度▽P与渗流流量Q之间的试验曲线，见图4。由图4可见，▽P～Q关系曲线皆呈下凸状，表明随着水力梯度的增大，渗流流量的增长幅度逐渐减小。 换言之，随着流量的增大，增加同等的流量所需消耗的水头也越来越大。另外，对于同一试样，围压增大可能引起岩样压缩，裂隙压密，过水通道减小，导水性降低，因此对于相同的流量，围压越大，所对应的水力梯度也越大，故在▽P～Q关系曲线图中表现为围压越大，曲线越偏离横轴，偏离程度与围压大小的变化基本保持一致。但也存在例外，例如试样3，在围压σ3达到25.0 MPa后，继续增大σ3对▽P～Q曲线的偏离作用略显微弱，因为此时裂隙的压密程度接近最大，岩样透水性基本不再变化。

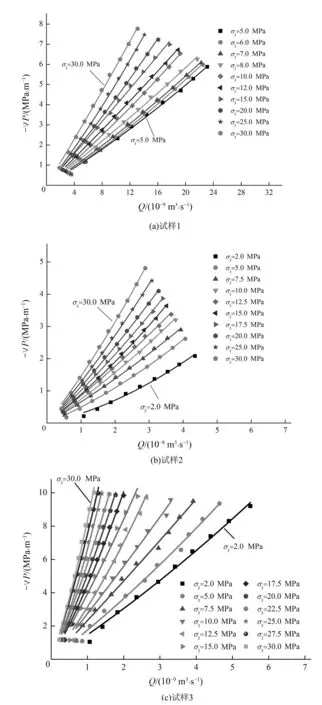
图4 试样在不同围压下的▽P～Q关系曲线Fig.4 Variation of pressure gradient ▽P with flow rate Q under various confining stresses

图4所示的▽P～Q非线性关系主要由水流惯性阻力作用的逐渐增强产生[14]，可采用Forchheimer(1901)提出的二项式方程来描述其渗流规律：

-▽P=AQ+BQ2

(2)

式中：▽P为压力梯度，Pa/m；Q为渗流流量，m3/s；A为线性项系数，(Pa·s)/m4；B为非线性项系数，(Pa·s2)/m7；Ah为过流面积，m2；μ为流体的动力黏度，Pa·s；ρ为密度，kg/m3；k为过流介质的固有渗透率，m2；β为非达西系数，m-1，又被称为紊流因子、非达西渗流惯性系数，是研究渗流非线性的重要参数[15-17]。

由式(1)可知，Forchheimer方程。在形式上仅仅是对达西方程增加了一个二次项(惯性项)，意义上则表示非达西渗流的能量损失不再仅由黏滞阻力控制，而是由黏滞阻力和惯性阻力2者共同决定[18]，换言之，渗流非达西效应取决于惯性阻力作用的相对大小。

图5 Forchheimer方程系数A和B与围压的关系曲线Fig.5 Variation of coefficients A and B with confining stress

采用Forchheimer非达西渗流方程对▽P～Q数据进行拟合，得到各曲线的拟合系数见表1。由表1可知，Forchheimer方程对非线性渗流的拟合效果很好，相关系数R2值均介于0.983 6和0.999 9之间，接近于1。为了更为直观地分析，图5给出了拟合系数A、B与围压的关系曲线。由图5可知，线性项系数A随围压严格单调递增，而非线性项系数B则随着围压的增大呈总体上升趋势。由式(2)可知，系数A反映的是破碎岩体的过流能力，围压增大，岩样内部的裂隙被压密，过流能力减弱，导致系数A增大；系数B表征流动的惯性效应，破碎岩样的裂隙分布复杂，形态各异，在围压增大的过程中，纵向裂隙闭合，横向裂隙扩展，2者对渗流的非线性具有相反的作用机制，且作用强度具有波动性，但总体上纵向裂隙作用强于横向裂隙作用，因而系数B在局部存在起伏波动，但总体上增大。

由Forchheimer方程的式(1)和式(2)可知，当忽略渗流流体的物理特性变化时，线性项系数A取决于岩石固有渗透率k，且与k成反比，非线性项系数B则由非达西系数β确定，并与之成正比。因此图5所示的系数A、B的变化关系在一定程度上反映了非达西系数β与固有渗透率k之间存在的相关关系；另一方面，在裂隙和多孔介质的渗流研究中，非达西系数β与固有渗透率k之间广泛采用幂函数关系描述[16,17,19,20]。基于本文的渗流试验结果，计算出3个破碎花岗岩岩样在各围压下的固有渗透率k与非达西系数β，并将2者关系曲线绘制于图6中，采用幂函数关系式进行拟合，相关系数R2=0.916 7，拟合程度较高，表达式如下：

β=6.962×10-13k-1.709

(3)

3 非达西渗流评估

如前所述，雷诺数Re和福希海默数F0是划分达西流和非达西流常用的指标，但是确定临界值却十分困难，因此本文在试验结果分析得到的非达西系数与固有渗透率关系式的基础上，建立另一类简单直观的非达西渗流评估方法。

表1 Forchheimer方程拟合系数Tab.1 The best-fitted coefficients of Forchheimer Equation

图6 非达西系数β与固有渗透率k关系曲线Fig.6 Variation of non-Darcy coefficient β with intrinsic permeability k

3.1 水力梯度比ΦP

假设破碎岩体的渗流流量Q已知，则由式(1)计算得到的非达西水力梯度|-▽P|F与由达西定律计算所得的达西水力梯度|-▽P|D2者的比值ΦP满足[14]：

(4)

上式表明非达西与达西水力梯度的比值ΦP由福希海默数F0决定，因此参数ΦP也具有表征渗流非达西程度的意义。将式(2)代入式(4)，并考虑式(3)所得的β～k幂函数关系，则有：

(5)

可知，ΦP是固有渗透率k和渗流流速v的函数。

根据式(4)和式(5)，图7(a)和图7(b)分别做出了ΦP～F0关系曲线和不同ΦP值下的v～k关系曲线。由图7可知，ΦP大于1，表明渗流惯性效应的存在将引起额外的压力损失，因此产生与达西流相等的流量需要更大的水力梯度。在评估渗流的非线性时，只要确定了水力梯度比ΦP的值，就可从图7(b)找到对应的临界v～k曲线，该曲线上部区域的渗流为非达西流，下部区域渗流的非线性则忽略不计，可采用达西定律进行渗流分析。虽然忽略非达西效应的渗流计算结果必然存在偏差，但只要在容许范围内则影响不大。假设某工程要求水力梯度的容许相对误差为10%，即对应临界水力梯度比ΦP=1.11(该值对应Zeng等[11]提出的达西流与非达西流的临界值F0=0.11)，图7(b)中ΦP=1.11对应v～k曲线即是相应的临界曲线。

图7 水力梯度比值ΦP评估图Fig.7 Evaluation of pressure gradient ratio ΦP

3.2 流量比ΦQ

假设破碎岩体的水力梯度|-▽P|已知，则由式(2)解得的非达西流量QF为[14]：

(6)

定义流量比ΦQ为非达西流量QF与由达西定律计算得到的达西流量QD的比值。为求得ΦQ，联立式(2)和达西方程，则：

AQD=AQF+BQ2F

(7)

故：

(8)

联立式(2)、式(3)和式(8)，得：

(9)

显然，ΦQ是固有渗透率k和水力梯度|-▽P|的函数。

同样地，根据式(8)和式(9)分别得出了ΦQ～F0关系曲线和不同ΦQ值下的|-▽P|～k关系曲线，见图8。由图8(a)可知，流量比ΦQ的值为0～1，因为在相同的水力梯度作用下，非达西流动的惯性项不可忽略，致使非达西流量小于达西流量。在评估渗流的非线性时，只要流量比ΦQ的值被确定后，就可以从图8(b)找到对应的临界|-▽P|～k曲线，该曲线下部区域的渗流可忽略非线性，采用达西定律进行渗流分析，其他区域的渗流作为非达西流处理。若流量的容许相对误差定为20%，则临界流量比ΦQ=0.83，图8(b)中ΦQ=0.83的|-▽P|～k曲线即是相应的临界曲线。

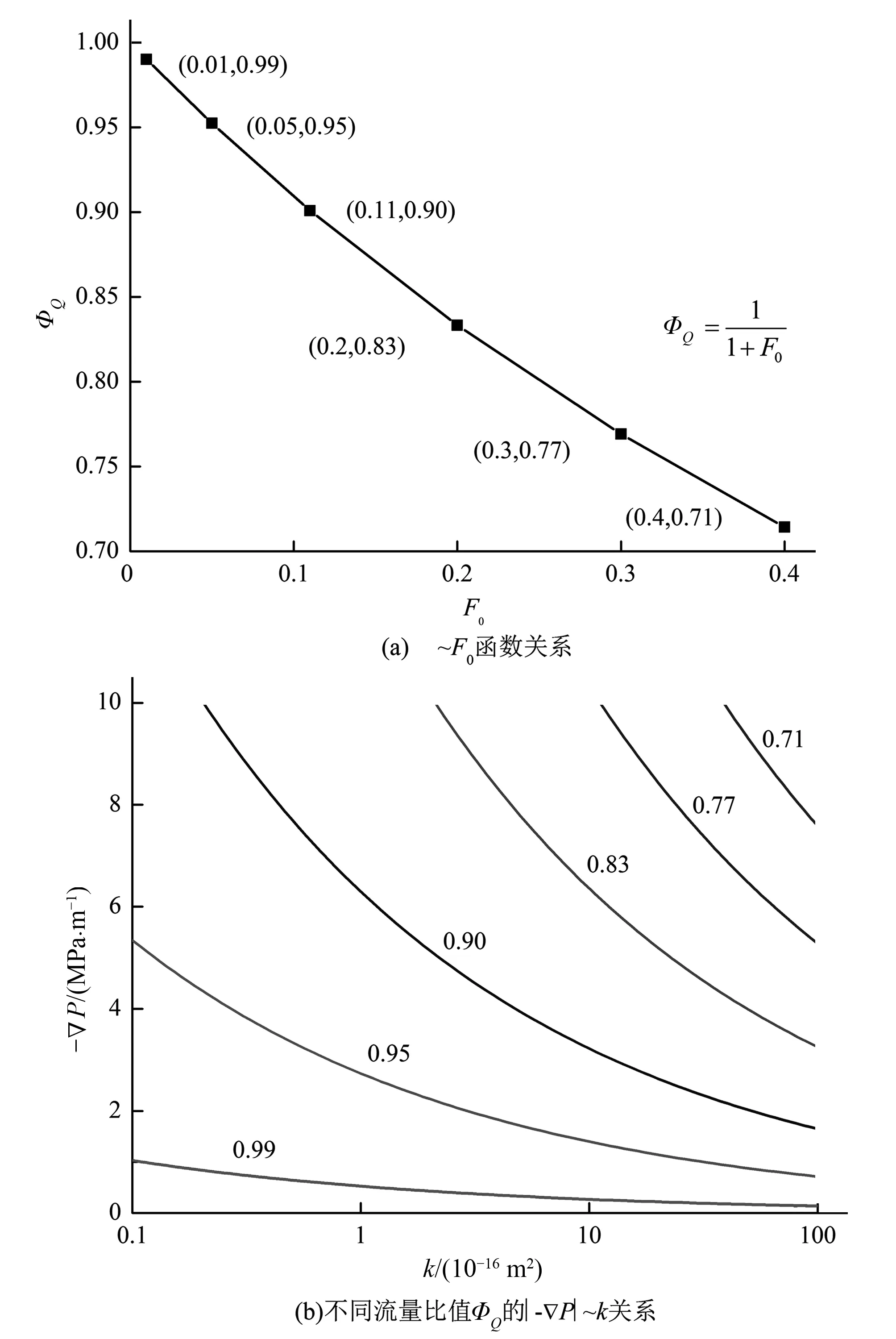
图8 流量比值ΦQ评估图Fig.8 Evaluation of flow rate ratio ΦQ

与雷诺数Re和福希海默数F0相比，水力梯度比ΦP和流量比ΦQ2个评估参数的物理意义更为清晰直观，通过限制非达西水力梯度或者非达西流量相对于达西流情况的偏离程度来判定渗流的非线性，对工程应用具有重要的意义。例如油气开发更关注开采量，因此可选择表示流量偏离的参数ΦQ来考虑渗流非线性，其临界值大小由工程实践中可容许的流量偏差决定；当分析与岩体渗透压力有关的稳定性问题时，选择水力梯度比ΦP来判定渗流非线性更为合适。但值得指出的是，式(5)和式(9)是在式(3)的基础上推导得到的，幂函数关系式(3)的拟合系数值与岩体介质的渗流特性有关，因此对于不同的透水介质，式(5)和式(9)中各系数值也会有所差异。

4 结 语

本文对3个阳江花岗岩破碎后，开展了不同围压条件下的高水力梯度渗流试验，并对之进行了分析讨论，在试验结果的基础上提出了一种简单直观的非达西渗流评估方法。具体得到如下结论。

(1)试验结果表明，破碎岩体中的渗流在高水力梯度下表现出显著的非线性，采用Forchheimer方程拟合▽P～Q关系的相关系数为0.983 6～0.999 9。

(2)随着围压的上升，与岩样过水能力有关的线性项系数A严格单调递增，反映渗流惯性阻力作用的非线性系数B呈总体增大趋势；非达西系数β与固有渗透率k具有相关性较好的幂函数关系。

(3)评估渗流的非线性时，采用水力梯度比ΦP和流量比ΦQ更加简单直观，且物理意义清晰，可根据工程具体情况，通过限制非达西流与达西流情况下2者的水力梯度比或者流量比来确定渗流非线性的临界条件，决定是否采用达西定律进行渗流分析。

□

[1] 黄先伍, 唐 平, 缪协兴, 等. 破碎砂岩渗透特性与孔隙率关系的试验研究[J]. 岩土力学, 2005,26(9):1 385-1 388.

[2] 李顺才, 缪协兴, 陈占清, 等. 承压破碎岩石非 Darcy 渗流的渗透特性试验研究[J]. 工程力学, 2008,25(4):85-92.

[3] Thauvin F, Mohanty K K. Network modeling of non-Darcy flow through porous media[J]. Transport in Porous Media, 1998,31(1):19-37.

[4] 胡大伟, 周 辉, 谢守益, 等. 峰后大理岩非线性渗流特征及机制研究[J]. 岩石力学与工程学报, 2009,28(3):451-458.

[5] Zhou J Q, Hu S H, Fang S, et al. Nonlinear flow behavior at low Reynolds numbers through rough-walled fractures subjected to normal compressive loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2015,80:202-218.

[6] 孟如真, 胡少华, 陈益峰, 等. 高渗压条件下基于非达西流的裂隙岩体渗透特性研究[J]. 岩石力学与工程学报, 2014,33(9):1 756-1 764.

[7] 李 健, 黄冠华, 文 章, 等. 两种不同粒径石英砂中非达西流动的实验研究[J]. 水利学报, 2008,39(6):726-732.

[8] Zimmerman R W, Al-yaarubi A, Pain C C, et al. Non-linear regimes of fluid flow in rock fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2004,41:163-169.

[9] Javadi M, Sharifzadeh M, Shahriar K, et al. Critical Reynolds number for nonlinear flow through rough-walled fractures: The role of shear processes[J]. Water Resources Research, 2014,50(2):1 789-1 804.

[10] 周创兵, 陈益峰, 姜清辉, 等. 复杂岩体多场广义耦合分析导论[M]. 北京: 中国水利水电出版社, 2008.

[11] Zeng Z, Grigg R. A criterion for non-Darcy flow in porous media[J]. Transport in Porous Media, 2006,63(1):57-69.

[12] Macici P, Mesini E, Viola R. Laboratory measurements of non-Darcy flow coefficients in natural and artificial unconsolidated porous media[J]. Journal of Petroleum Science and Engineering, 2011,77(3):365-374.

[13] Liu R, Li B, Jiang Y. Critical hydraulic gradient for nonlinear flow through rock fracture networks: the roles of aperture, surface roughness, and number of intersections[J]. Advances in Water Resources, 2016, 88:53-65.

[14] Chen Y F, Zhou J Q, Hu S H, et al. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J]. Journal of Hydrology, 2015,529:993-1 006.

[15] Firdaouss M, Guermond J L, Quéré L P. Nonlinear corrections to Darcy's law at low Reynolds numbers[J]. Journal of Fluid Mechanics, 1997,343:331-350.

[16] 许 凯, 雷学文, 孟庆山, 等. 非达西渗流惯性系数研究[J]. 岩石力学与工程学报, 2012,31(1):164-170.

[17] Geertsma J. Estimating the coefficient of inertial resistance in fluid flow through porous media[J]. Society of Petroleum Engineers Journal, 1974,14(5):445-450.

[18] Zhou J Q, Hu S H, Chen Y F, et al. The friction factor in the forchheimer equation for rock fractures[J]. Rock Mechanics and Rock Engineering, 2016,49(8):3 055-3 068.

[19] Li D, Engler T W. Literature review on correlations of the non-Darcy coefficient[C]∥SPE Permian Basin Oil and Gas Recovery Conference. Society of Petroleum Engineers, 2001.

[20] 王 媛, 秦 峰, 夏志皓, 等. 深埋隧洞涌水预测非达西流模型及数值模拟[J]. 岩石力学与工程学报, 2012,31(9):1 862-1 868.