平面近场测试中误差分析方法的研究

孙士林,陈玉林

(华东电子工程研究所，合肥 230031)

0 引 言

平面近场测试一次测量即可以确定天线远场特性的完整信息，而且可以在室内进行，这不仅使工作人员得到相对舒适的工作场所，而且提供了一个可以控制的测试环境和全天候工作条件。

但对任何一种测量技术，首要考虑的内容之一就是对误差真实的估计，特别是对于近场技术，包含了大量数学方法，其难度的最大因素也在于其数学上的复杂性。另外，暗室因为集成了大量仪表等因素，环境十分复杂，故需要对暗室误差进行详尽分析和评估，以了解各项误差对天线远场方向图的影响。传统的误差评估方法是通过对比给定天线的近场测量和远场测量结果，将这两种方法的差别作为近场测试技术的误差测量结果，但这种方法的局限性在于：(1)这种方法评估的误差受远场测量中的误差影响；(2)不能确定每种误差对最终结果的影响；(3)某些种类的天线只适用于近场测量，无法用远场方法来测量[1]。

但是在目前国内对测量准确度的评定中，存在方法不统一，且存在混淆分析中概念的问题，为了明确解决这些问题，笔者根据近几年对近场测试误差分析方面的研究，结合国内外测试误差分析的发展，明确了误差分析中的相关概念，对误差分析使用的方法进行了研究，并给出了分析的实例。

1 误差分析中相关概念

评定测量准确度有误差和不确定度两个概念。一般国内容易将两者混为一谈，其实两者是有明显区别的。

1.1 误差的概念及计算方法

所谓误差就是测得值和被测量的真值之间的差，即误差=测得值-真值。测量误差可用绝对误差表示，也可用相对误差表示。绝对误差=测得值-真值。相对误差=绝对误差/真值。误差分为随机误差、系统误差和粗大误差。粗大误差值较大，明显歪曲测量结果，很容易发现，在此不作讨论。随机误差和系统误差有着相反的特性，随机误差可以在尽可能相同的测量条件下通过重复测量来量化，而系统误差则需要通过有意改变测量条件来量化[2-3]。

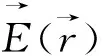
(1)

副瓣电平的相对误差定义为：

(2)

通常副瓣电平的误差用dB来表示，进一步推导，得到：

(3)

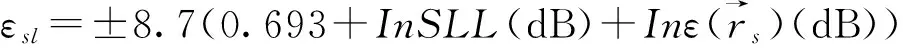
1.2 不确定度的概念及计算方法

测量不确定度是对测量结果可能误差的度量，也是定量说明测量结果质量好坏的一个参数。因此，一个完整的测量结果，除了应给出被测量的最佳估计值外，还应同时给出测量结果的不确定度[5]。

对不确定度评估技术的理解基于四个方面的研究和假设：(1)所有重要的误差源被识别和列出。(2)所有近场误差源可以被测量和评估，并且在很多情况下可以确定误差的函数公式。例如，需要使用激光设备去测量X，Y，Z位置误差，然后利用函数公式计算其副瓣不确定值。(3)可以推导出误差方程式或者开发测试方法去确定近场测量误差和远场结果之间的关系。(4)可以将各独立的误差源所产生的不确定度合并得到一个总的不确定度评估结果[6]。

对不确定的计算对于可采用全域分析方法。全域分析基于正态分布性质，对方向图所有点的ESS(即误差)来取均方根(RMS)。RMS对应于正态分布中的标准差，则不确定度可以根据下式计算出[7]：

不确定度(dB) =±20*LOG(1+10^(RMS-SLL)/20)

式中，SLL=所要分析的副瓣电平(dB)

因为主瓣区域能量的微小变化便能导致很大的误差，而我们主要是分析副瓣区域的影响，所以要将主瓣区域的误差去掉再对其余部分求RMS。

2 计算实例

为说明近场测试中误差分析的具体过程，下面给出了评估位置误差项不确定度的实例。

2.1 计算机模型

如图1所示，在坐标系xoy中，阵列天线由n个对称阵子组成，阵子水平和垂直单元间距分别为dx和dy，采样面到天线的距离为d。

对图1的计算模型，引入一定类型的位置误差，对引入误差后的近场数据进行近远场变换，得到带误差的远场方向图，然后将其与理论远场方向图进行比较，得到误差曲线，对误差曲线进行分析计算，即可得到探头位置误差对副瓣影响的量级。

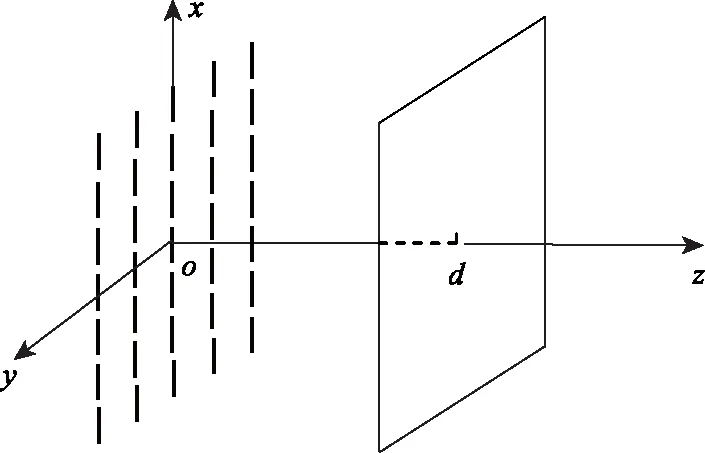
图1 计算模型示意图

2.2 计算结果及讨论

①不引入位置误差：

图2给出了理论远场方向图和由理论近场得到的远场方向图对比，从图中可以看出二者吻合得很好，这说明计算中所选择的扫描面的宽度已足够大，由于有限扫描面截断所引起的截断误差可忽略不计。根据上述对误差曲线的计算方法，得到RMS值为-78.36，则其对-50 dB副瓣的不确定度为0.33 dB。

图2 理论远场方向图与由理论近场得到的远场方向图的比较

②引入位置误差：

假定x方向位置误差服从均值为零、均方差为σx的正态分布；z方向位置误差服从均值为零、均方差为σz的正态分布。图3给出了理论远场方向图、当σx=0.003λ，σz=0.003λ时由引入位置误差后的近场得到的远场方向图的对比。

图3 远场方向图的比较(σx=0.003λ，σz=0.003λ)

通过对图3中误差曲线的计算，得到RMS值为-55.39，其对-50 dB副瓣的不确定度为3.74 dB。

3 结 语

针对目前国内对近场测试中误差的分析无统一方法的问题，文章首先区分了误差和不确定度的概念，并且对其如何计算进行了说明，最后给出了平面近场测试中误差分析的实例，这对平面近场测试中误差的分析有一定的指导意义。

[1] 张福顺，张进民．天线测量[M] ．西安:西安电子科技大学出版社，1995.

[2] 杨莘元，孙继禹等．超低旁瓣天线平面近场测量中随机误差对远场方向图的影响.哈尔滨工程大学学报，2004，25(2)：200-203．

[3] 李勇．平面近场天线测量误差分析.电子测量与仪器学报，2010，Vol.24，No.11：987-992．

[4] Greg Masters. 18-term range error assessment.NSI near filed system,INC,29 January 2013．

[5] 吴石林．误差分析与数据处理[M].北京：清华大学出版社，2010.

[6] 林洪桦．测量误差与不确定度评估[M] ．北京:机械工业出版社，2009.

[7] A. D. Yaghjian, “Techniques for reducing the effect of measurement errors in near-field antenna measurements,”Nat.Bur.stand.Internal.Rep.83-1689, May, 2011．