城市轨道交通进站客流量短时组合预测模型
李得伟, 颜艺星, 曾险峰
(1. 北京交通大学轨道交通控制与安全国家重点实验室, 北京 100044; 2. 广州铁路职业技术学院, 广州 510430)
城市轨道交通进站客流量短时组合预测模型
李得伟1, 颜艺星1, 曾险峰2
(1. 北京交通大学轨道交通控制与安全国家重点实验室, 北京 100044; 2. 广州铁路职业技术学院, 广州 510430)
高精度的短时进站客流量预测对城市轨道交通日常客流组织具有重要意义,利用客流预测结果在事前实施限流、疏导等措施,较事后控制更及时、先进。通过采集15 min间隔的地铁进站客流数据,利用上周同期进站量、本日上一时段进站量以及高峰和非高峰时段参数作为输入变量,尝试分别采用加权历史平均自回归模型、ARIMA模型及小波神经网络模型进行短时预测,以获得精度最高的模型。在此基础上,进行三种方法组合预测,探究组合预测效果。通过案例分析,发现当考虑时段因素时,小波神经网络预测精度最高,为91.05%;ARIMA模型误差结构最好。当采用所提出的组合预测模型后,预测精度指标较独立预测模型均有提升,但误差结构没有得到改善。研究表明,所提组合预测模型可以有效地应用于城市轨道交通进站客流的短时预测中。
城市轨道交通; 进站客流量; 短时预测模型; 组合预测
城市轨道交通已成为许多大城市公共交通体系中的重要部分。为有效控制运营成本、提高运输效率,根据客流在短时间内的波动,动态调整运输组织方案已成为城市轨道交通运营管理重要的发展方向,城市轨道交通进站客流量短时预测是其中的基础核心问题。实时、准确地预测未来时段的客流量,及时掌握客流波动情况,能够为运能与运量的动态匹配提供客观依据,有助于运营部门及时调整运输计划并组织有效运力,亦有助于运营部门进行科学的客流诱导、管理与控制工作。
国内外短时交通预测主要应用在道路领域,基本形成了较为通用的预测方法[1]。已有预测模型可分为基于参数的模型、基于非参数的模型及混合模型。基于参数的模型是建立在统计学基础上的,包括历史平均模型[2]、非线性回归[3,4]、平滑模型[5]、ARIMA模型[6]、利用卡尔曼滤波方法的状态空间模型[7]等。这类模型的本质是对均值的预测,无法预测极值。随着数据采集手段的进步及历史数据量的增加,出现了非参数模型,包括最近邻居法[8]、神经网络[9]、贝叶斯模型[10]、支持向量机[11]、模糊逻辑[12]等。非参数模型的优点是鲁棒性较强,能够解决极值预测的问题。非参数模型的本质是数据驱动模型,只有历史数据样本足够大时,精度才能达到要求。为充分发挥二者的优点,近年来,出现了将这两类方法混合建模[13]的发展趋势,如混合ARIMA和神经网络模型,混合模糊逻辑与神经网络等。城市轨道交通客流预测研究人员基本沿用了道路交通流预测中的方法,文献[14-20]分别采用参数和非参数模型对城市轨道交通短时客流进行预测。
笔者结合“北京市地铁客流状态监测、预警及辅助决策系统研制及示范应用”的实际应用需求,基于实时采集的进站客流数据,提出一种进站量短时组合预测方法。第二部分主要介绍预测模型的机理;第三部分通过案例介绍模型的预测效果;第四部分为结论。
1 进站量短时组合预测模型机理
1.1 定义
本文所研究的城市轨道交通进站客流量短时预测是指基于已知某车站的历史和实时进站客流数据,采用一定数学模型,预测下一时段该站进站量的过程。
1.2 预测模型
1.2.1 基本结构
为克服已有研究中单一预测模型的缺点,本文采用线性组合预测模型,基本模型为
(1)

1.2.2 子模型选择
对比研究已有的短时预测模型,得到各模型优缺点如表1所示。
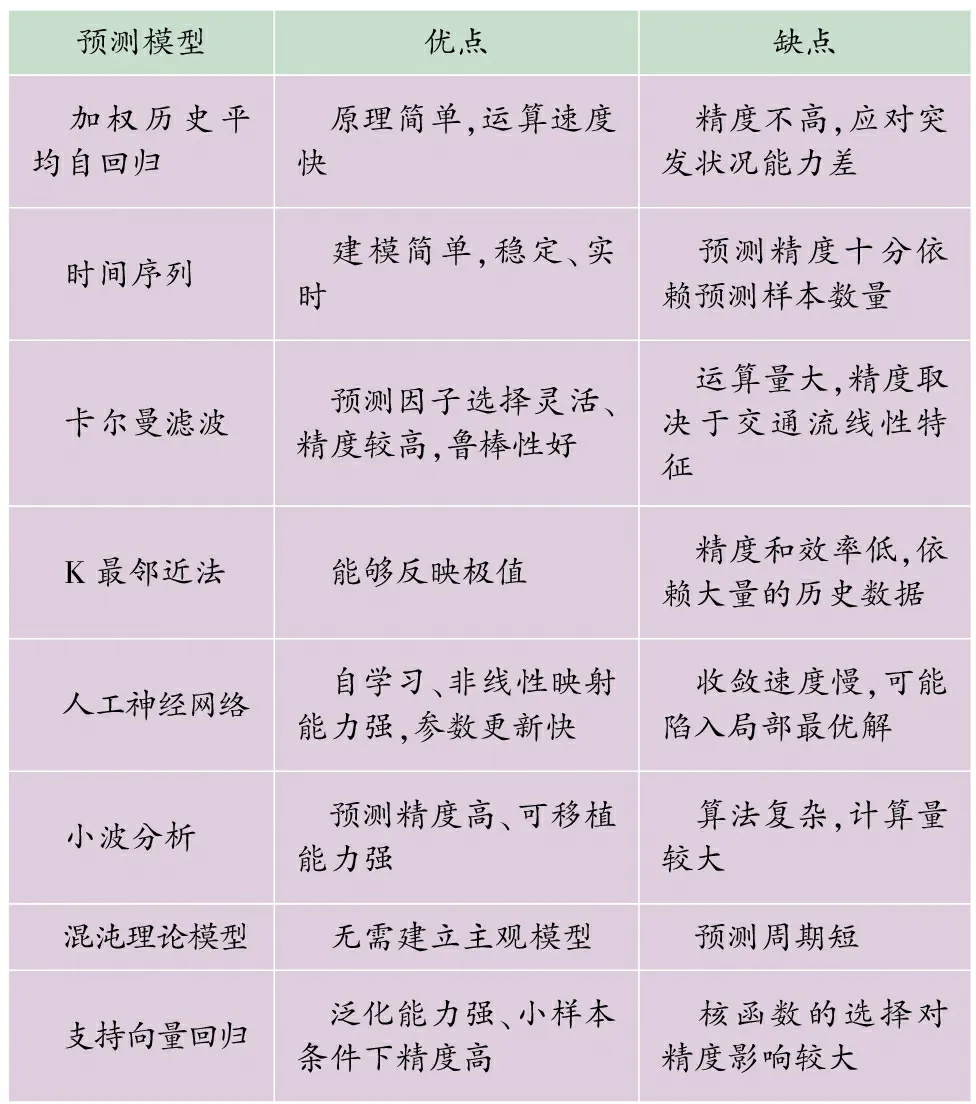
表1 已有短时预测模型对比
城市轨道交通系统是一个有人参与的、时变的复杂巨系统,具有高度不确定性和非线性,短时客流的时变性和不确定性高。因此,用于短时客流预测的模型应具有以下特性:
1) 实时性——预测能够及时反映交通状态的实时变化;
2) 准确性——预测精度应该在合理范围内,预测误差能够被使用者接受;
3) 可靠性——模型应具有较好的抗噪能力。
城市轨道交通客流进站量随着时间呈现有规律的变化,可将其视为时间序列处理,加权历史平均自回归模型和ARIMA模型两者作为经典的线性时间序列模型,原理清晰,前者较后者多历史信息。人工神经网络具有强大的学习能力,非线性映射能力强,而小波变换具有良好的多分辨分析能力,适用于对具有时空特性的进站客流量进行分析。因此,考虑在组合预测子模型中采用加权历史平均自回归模型、ARIMA模型等两个参数模型及小波神经网络非参数模型。
1.2.2.1 子模型1:加权历史平均自回归模型
利用预测对象的时间序列在不同时期取值之间存在的关系,建立回归方程进行预测。通过客流特性分析与历史数据对比发现,城市轨道交通进站量与历史同期进站量有较强的相关性,同时也受当前进站趋势的影响。考虑到模型的输入数据,结合城市轨道交通客流时空分布周期性特点,构造加权历史平均自回归模型,即
(2)
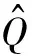
1.2.2.2 子模型2:ARIMA模型
ARIMA模型思想是对非平稳的时间序列进行若干次差分运算,使之转换为平稳序列,并分解为趋势量和随机量两部分。预测模型为
εt-θ1εt-1-…-θqεt-q
(3)

1.2.2.3 子模型3:小波神经网络
本文使用的小波神经网络是一种以BP神经网络拓扑结构为基础,把小波基函数作为隐含层节点的传递函数,信号前向传播的同时误差反向传播,其网络权值和小波基函数参数的修正方法与BP神经网络相同。该神经网络有一个输入层,一个隐含层和一个输出层,采用的小波基函数为Morlet母小波基函数,即
(4)
由于高峰期客流与平峰期客流有较大差别,因此,在上一步的基础上,考虑将时间因素增加至小波神经网络输入中。高峰时段和平峰时段分别对应“1”和“0”,输出保持不变,得到考虑时间因素的小波神经网络预测模型。
1.2.3 组合预测参数的确定
组合预测的目标是尽可能缩小预测值与实际值之间的误差,若用平均百分比误差表示,则组合预测参数可以表示为优化模型,即
(5)
1.3 精度判断标准
为判定模型的预测精度,采用平均绝对误差(MAE)、平均绝对百分误差(MAPE)及均方根误差(RMSE)指标,即
(6)
(7)
(8)
2 案例分析
以北京“地铁客流状态监测、预警及辅助决策系统研制及示范应用”为背景,选择北京市地铁13号线回龙观站为案例。所有的客流数据均实时采集自AFC系统,由于数据压缩和传输环节需耗费一定时间,进站客流实时传入系统的时间粒度为每15 min 1次,因此,采用预测间隔均为15 min。全天传输时间域为5:00至23:00,每日共72组进站客流数据,用序号1~72表示。利用2014年9月11日—24日连续两周客流进站数据标定模型参数和训练样本。然后,利用所标定的模型,预测2014年9月25日每个时段的进站客流量。
2.1 参数标定
1) 子模型1的参数标定可利用公式(2)反推直接计算各时段wt的值,结果从略。
2) 子模型2的参数标定采用EVIEWS软件,通过分析全天进站客流量差分序列的结尾特性判断,得到p=7,q=6,此时,预测方程如下:
(9)
3) 子模型3的参数标定方法为:首先计算预测时段的进站客流量与前5个时段进站客流量的Spearman相关系数,所得结果如表2所示。

表2 预测时段与前5个时段客流量相关系数
从表2可以看出,预测时段的进站客流量与前时段客流量有很强的相关性,选取相关性较高的前3个时段的客流量作为输入构成神经网络输入矩阵。
4) 组合预测模型的权重参数采用子模型1、2、3的预测结果和模型(5),利用最小二乘法进行标定,得到C=-2.536,Κ1=0.328,Κ2=0.080,Κ2=0.599。
2.2 预测结果分析
各模型预测的结果如图1所示,预测性能指标如表3所示。
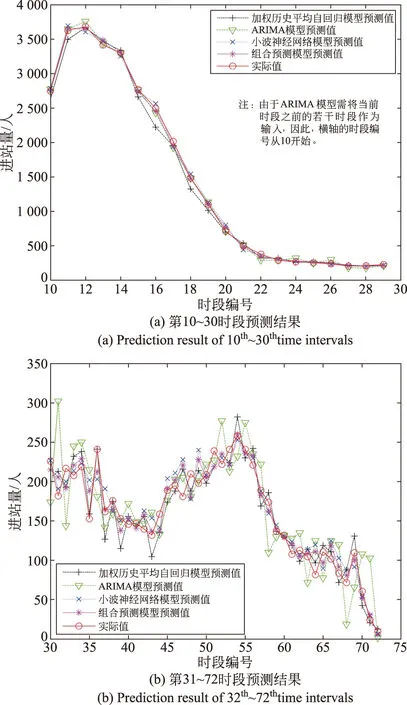
图1 各模型预测结果对比 Fig.1 Comparison of prediction results of different models
首先分析各子模型单独预测性能。对比MAE,考虑时间因素的小波神经网络模型误差最小为23.22,只考虑客流因素的小波神经网络模型的误差为25.91,加权历史自回归模型、ARIMA模型的值较为接近,分别为31.82和31.66,小波神经网络明显优于前两个模型。对比MAPE,考虑时间因素的小波神经网络模型误差最小,为8.95%,其次是加权历史平均自回归模型,为9.86%,接下来是输入只考虑客流因素的小波神经网络模型为 10.09%,最后是ARIMA模型。对比RMSE,考虑时间因素的小波神经网络值最优,其值为31.45,其次是输入只考虑客流因素的小波神经网络模型,接下来是ARIMA模型,最后是加权历史平均自回归模型。综合考察以上3项指标,输入考虑时间因素的小波神经网络预测精度最高。

表3 各模型的预测性能指标
其次,对比组合预测模型和各子模型预测结果发现,组合预测模型MAE、MAPE、RMSE分别为16.27,7.84%,22.52,均优于任何一个单独预测模型的精度。
2.3 误差分析
首先进行分时段预测误差对比,如图2所示。
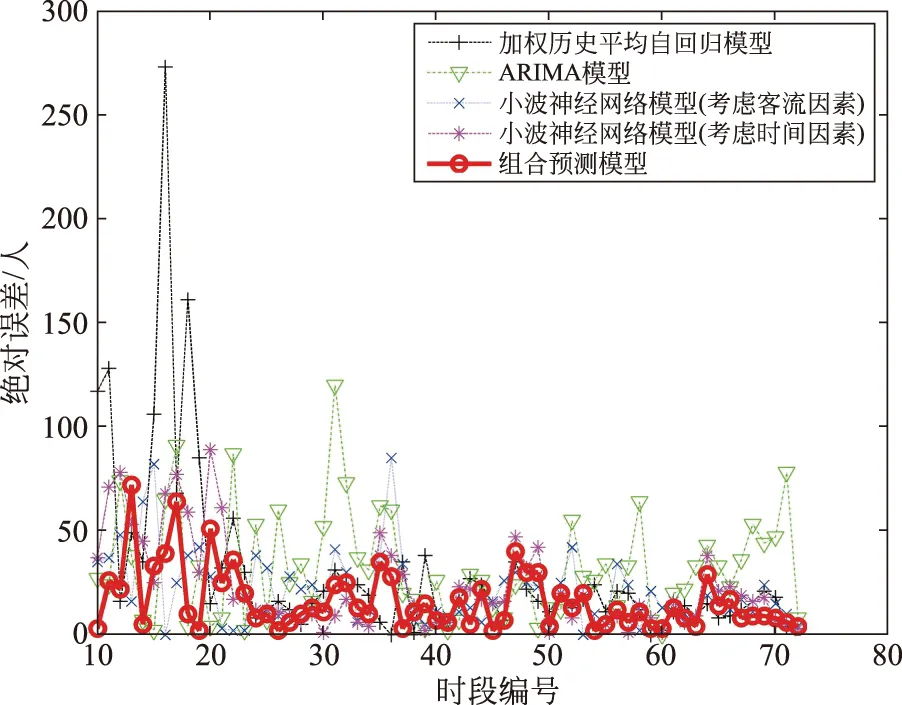
图2 各模型独立预测误差随时段分布 Fig.2 Temporal distribution of prediction errors for different models
可以看出,加权历史平均自回归模型在对时段14~18,即8:15— 9:30期间的预测误差较大,最大值为274人,对后续时段的预测误差除时段13:00—13:15以外,基本都保持在25人以下。ARIMA模型的预测误差在预测时段内没有特别剧烈的变化,但是误差值相对其他模型一直偏大。输入只考虑客流因素的小波神经网络预测误差在所有预测时段都保持较低水平,最大预测误差85出现时段36代表的13:45—14:00。输入考虑增加时间因素的小波神经网络在时段11的预测误差较大,最高为89,随着时间向后推移误差逐渐减小。组合预测误差随时间分布较平稳。
其次,分析误差分布。分别以±10%和±20%作为阈值上下限,研究不同模型预测结果中过低预测(低于阈值下限)和过高预测(高于阈值上限)的时段数量占总时段数量的比值,如表4所示。

表4 各模型误差分布
可以看出,采用±10%作为阈值时,加权历史平均自回归模型、ARIMA模型和考虑时间因素的小波神经网络模型过高预测和过低预测的比例较接近;当采用±20%作为阈值时,只有ARIMA模型能够保证过高预测和过低预测的比例接近。此时,加权历史平均自回归模型的预测结果偏低,而神经网络预测结果偏高。采用组合预测模型时,过低预测比例和过高预测比例与考虑时间因素的小波神经网络相同,表明尽管组合预测提高了预测精度,但是未改善误差的结构。
3 结论
本文提出将加权历史平均自回归模型、ARIMA模型和小波神经网络组合,进行城市轨道交通进站量短时预测,通过各模型预测结果的对比分析,发现单独预测时小波神经网络预测模型效果最好,组合预测模型优于所有单一预测模型,但并没有改善误差结构。组合预测是近年来国际上短时客流预测的主要发展方向,其优势是预测精度高,但同时,在实际应用中,当不同子模型的预测结果出现较大差异时,可能会对决策者带来子模型的选择困惑。今后的研究可从3个方面展开:一是尝试采用非线性函数进行组合预测;二是探讨组合更多不同特点的方法;三是尝试对更多非正常场景客流进行预测。

[2] SMITH B L, DEMETSKY M J.Traffic flow forecasting: comparison of modelling approaches[J].Journal of transportation engineering, 1997, 123(4): 261-266.
[3] MU T, JIANG J, WANG Y.Heterogeneous delay embedding for travel time and energy cost prediction via regression analysis[J].Intelligent transportation systems, IEEE transactions on intelligent transportation systems, 2013, 14 (1): 214-224.
[4] VLAHOGIANNI E I, KARLAFTIS M G, Golias J C. Temporal evolution of short-term urban traffic flow: a non linear dynamics approach[J].Computer-aided civil and infrastructure engineering, 2008, 23(7): 536-548.
[5] WILLIAMS B M, DURVASULA P K, BROWN D E.Urban freeway traffic flow prediction: application of seasonal autoregressive integrated moving average and exponential smoothing models [J]. Journal of the transportation research record, 1998(1): 132-144.
[6] WILLIAMS B M, Hoel L A.Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results[J].Journal of transportation engineering, 2003, 129(6): 664-672.
[7] CHIEN S I J, KUCHIPUDI C M.Dynamic travel time prediction with real-time and historical data[C]//Proceedings of the Transportation Research Board 81st Annual Meeting, Washington, DC.2002: 1-10.
[8] SMITH B L, WILLIAMS B M,KEITH O R.Comparison of parametric and nonparametric models for traffic flow forecasting[J].Transportation research Part C: emerging technologies, 2002, 10(4): 303-321.
[9] VLAHOGIANNI E I, KARLAFTIS M G, GOLIAS J C.Optimized and meta-optimized neural networks for short-term traffic flow prediction: a genetic approach[J].Transportation research part C: emerging technologies 2005,13 (3): 211-234.
[10] KHAN, A M.Bayesian predictive travel time methodology for advanced traveller information system [J].Journal of advanced transportation 2012, 46(1): 67-79.
[11] ZHANG Y, XIE Y. Forecasting of short-term freeway volume with v-support vector machines [J].Journal of the transportation research record, 2007, 2024: 92-99.
[12] ZHANG Y, YE Z.Short-term traffic flow forecasting using fuzzy logic system methods [J].Journal of intelligent transportation systems: technology, planning, and operations, 2008, 12 (3): 102-112.
[13] ZHANG N, ZHANG Y, LU H.Seasonal autoregressive integrated moving average and support vector machine models: Prediction of short-term traffic flow on freeways[J].Journal of the transportation research record, 2011, 2215: 85-92.
[14] 史文雯.城市轨道交通短时客流预测与最优客运能力调配问题的研究[D].北京:北京交通大学,2011.
SHI Wenwen.Study on short-term passenger flow forecast the optimal capacity allocation problem in urban mass transit[D].Beijing: Beijing Jiaotong University, 2011.
[15] 谢婉泽.城市轨道交通客流短时预测方法与运营编组优化设计[D].大连:大连交通大学,2013.
XIE Wanze.Passenger flow short-time prediction and marshalling optimization of urban rail transit[D].Dalian: Dalian Jiaotong University, 2013.
[16] 董升伟.基于改进BP神经网络的轨道交通短时客流预测方法研究[D]. 北京:北京交通大学, 2013.
DONG Shengwei.The research of short-time passenger flow forecasting based on improved BP Neural network in urban rail transit[D].Beijing: Beijing Jiaotong University, 2013.
[17] 谢辉,董德存,欧冬秀,等.轨道交通短期客流预测方法及其算法研究[J].现代城市轨道交通,2011(3):96-99.
XIE Hui, DONG Decun, OU Dongxiu, et al.Short-time passenger flow forecasting method and algorithm in rail transit[J].Modern urban transit, 2011(3): 96-99.
[18] 邓军生,孔繁钰,陈小峰,等.基于SVR的轨道交通客流量预测[J].重庆科技学院学报(自然科学版),2008,10(3):147-149.
DENG Junsheng, KONG Fanyu, CHEN Xiaofeng, et al. Passenger flow forecast of urban rail transit based on support vector regression[J].Journal of chongqing technology college (natural science edition), 2008, 10(3): 147-149.
[19] 杨军.地铁客流短期预测及客流疏散模拟研究[D].北京:北京交通大学,2013.
YANG Jun.Research on metro passenger flow short-time prediction and evacuation simulation[D].Beijing: Beijing Jiaotong University, 2013.
[20] 四兵锋,何九冉,任华玲,等.基于时序特征的城市轨道交通客流预测[J].北京交通大学学报(自然科学版),2014,38(3):1-6.
SI Binfeng, HE Jiuran, RENG Hualing, et al.Urban railway traffic passenger flow forecast based on the timing characteristics[J].Journal of Beijing Jiaotong University (natural science edition), 2014, 38(3): 1-6.
(编辑:曹雪明)
Combined Short-term Prediction Model of Station Entry Flow in Urban Rail Transit
LI Dewei1, YAN Yixing1, ZENG Xianfeng2
(1.State Key Lab of Rail Traffic and Control, Beijing Jiaotong University, Beijing 100044; 2.Guangzhou Railway Polytechnic, Guangzhou 510430)

urban rail transit; passenger entry flow; short-term prediction model; combination prediction
10.3969/j.issn.1672-6073.2017.01.012
2016-04-01
2016-12-12
李得伟,男,副教授,博士,从事轨道交通运输组织研究,lidw@bjtu.edu.cn
北京市自然科学基金(9132015);基本科研业务费(2016JBM030);北京市高等学校青年英才计划(YETP0555)
U293.5
A
1672-6073(2017)01-0054-05

