基于适合分析T样条的高阶数值流形方法1)

刘登学张友良刘高敏,†

∗(中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，武汉430071)

†(中国科学院大学，北京100049)

基于适合分析T样条的高阶数值流形方法1)

刘登学∗,†,2)张友良∗刘高敏∗,†

∗(中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，武汉430071)

†(中国科学院大学，北京100049)

数值流形方法是一种非常灵活的数值计算方法，连续体的有限单元方法和块体系统的非连续变形分析方法只是这一数值方法的特例.数值流形方法中高阶位移函数的构造可通过提高权函数的阶次来实现，这种方法往往需要沿单元边界配置适当的边内节点，这些结点的出现增加了前处理的复杂性，特别是对于大型复杂的空间问题.另一方面，在数值流形方法中可通过缩小单元尺寸(h加密)来提高求解精度.当模拟裂纹扩展时，这种细化策略可用来克服裂纹尖端的奇异性.一个传统的解决方案是细化整个网格，但这会导致计算效率的显著降低.将适合分析的T样条(analysis-suitable T-spline，AST)引入数值流形方法中来建立高阶数值流形方法的分析格式，有效的避免了该问题的出现.AST样条基函数具有线性无关，单位分解，局部加密等许多重要性质，使得其非常适合用于工程设计及分析.在引入AST样条后，可通过改变数学覆盖的构造形式建立不同阶次的数值流形方法分析格式；AST样条自身的局部加密性质也使得数值流形方法中的数学网格局部加密更容易实现.算例结果表明：随着AST样条基函数阶次的提高，数值流形方法的计算结果有了明显的改善；基于AST样条基函数的数值流形方法在保持计算精度的前提下降低了自由度的数量.

高阶数值流形方法，线性相关，适合分析的T样条，局部加密

引言

1992年，石根华提出了在岩石工程中具有重要影响的数值流形法[1-2](numerical manifold method, NMM).该方法非常适合断续节理岩体的模拟，是一个在统一数学框架下的岩石小变形开裂与非连续大位移分析的一体化计算方法.数值流形方法自提出以来，已在岩土工程诸多领域得到成功应用，如隧道的开挖模拟[3-5]、岩体的锚固[6-7]、岩体裂纹扩展[8-12]以及岩体的饱和渗流分析[13].通常可以通过以下几种方式来提高数值流形方法的求解精度：覆盖函数采用高阶次的多项式；提高权函数的阶次；减小流形单元的尺寸，即单元加密.姜清辉等[14]采用一阶覆盖函数代替常覆盖函数，建立了三维高阶数值流形方法的分析格式.苏海东等[15-16]基于平面三角形数学网格和多项式覆盖函数，提出高阶流形法的两种初应力的处理方法.Wang等[17]提出了一种二阶数值流形方法模型用以解决具有自由表面水流的非线性问题.然而，高阶数值流形方法在提高计算精度的同时，也会引起总体刚度矩阵奇异，即线性相关.针对该问题Zheng等[18]提出在数值流形方法中物理覆盖上的局部位移函数采用一阶泰勒展开式，建立了线性无关的高阶数值流形方法，郭朝旭等[19]提出了改进的LDLT算法，可快速稳定的求得一个特解.蔡永昌等[20]提出了一种基于独立覆盖的高阶流形方法，消除了高阶流形方法特有的线性相关带来的总体刚度矩阵奇异性的问题.Fan等[21]将位移的导数作为自由度引入到数值流形方法中，建立了一种新型的高阶数值流形方法，避免了线性相关的问题.在提高权函数阶次方面，通常是通过沿单元边界配置适当的内结点来实现，这些结点的出现增加了前处理的复杂性，特别是对于大型复杂的空间问题.

等几何分析 (isogeometric analysis)是 Hughes等[22]于 2005年提出的一个将计算机铺助设计和计算机辅助工程相接合的一种数值分析方法.它的基本思想是将用来表示几何造型的基函数同时用来定义未知场变量，如位移、温度等.最常用的基函数是非均匀有理B样条(non-uniform rational B spline, NURBS).NURBS有很多优点：可以进行任意表面的建模；拥有很多优良的数学特性，如非负性、单位分解特性、基函数的线性无关性、局部支撑性等.随着研究的深入，NURBS本身的不足也不断暴露出来[23]，如 NURBS采用张量积形式，使得局部网格细化效率不高，很多形状无法用一个简单封闭的NURBS面表示；面与面交界处有间隙或重叠等.为了克服这些不足，许多学者开始将T样条用于等几何分析中.Sederberg等[24]最早将T样条引入计算机制图，并且提出了T样条的局部加密算法；Bazilevs等[25]探索了基于T样条基函数的等几何分析，用于简单的流体力学和结构力学的计算，获得了很好的效果.Zhang等[26]基于等几何分析的思想，推导了基于二次B样条的9节点数值流形方法分析格式，提出了一种数值流形T样条局部加密方法.有些情况下，T样条的局部加密会出现不适合分析的单元；另外T样条的混合函数的线性无关性在一般T网格上不能保证，可能导致刚度矩阵奇异.为此Li等[27]提出了适合分析的T样条(analysis-suitable T-spline，AST)来克服上述问题.本文将AST样条引入到数值流形方法中，建立了基于AST样条函数的高阶数值流形方法分析格式.

1 数值流形方法简介

1.1 数值流形方法基本概念

数值流形方法是基于三个基本概念建立起来的：数学覆盖、物理覆盖、流形单元.数学覆盖系统是许多可重叠小片的并集，覆盖整个问题区域.每一个小片称为一个数学覆盖，记为Mi(i=1,2,··,nM).物理覆盖系统由数学覆盖和物理网格两者组成，物理网格包括材料体的边界、裂缝、块体边界、不同材料区域的交接面.如果裂缝或者块体边界把一个数学覆盖Mi分成两个或更多的完全不连续区域，这些区域称为物理覆盖，记为因此物理覆盖是不连续裂缝对数学覆盖的再剖分.正是由于引入了数学覆盖和物理覆盖两套覆盖系统，数值流形方法可以统一地解决连续和非连续问题.流形单元定义为几个物理覆盖的公共部分.

为了更清楚的说明这3个概念，给出如图1所示的一个例子.对于图中含一条裂纹的不规则多边形板，数学覆盖系统采用规则矩形网格，共享结点i的4个矩形组成一个数学覆盖，记为Mi.数学覆盖M1与裂纹相交形成两个物理覆盖数学覆盖M2，M3，M4，M5没有与物理网格相交，各自形成一个物理覆盖p2，p3，p4，p5，物理覆盖与数学覆盖相同.如图中阴影所示，流形单元E(p2,p3,p4,p5)为物理覆盖p2，p3，p4，p5的公共区域，而流形单元E(p6,p7,p8,p9)为物理覆盖p6，p7，p8，p9的公共区域.流形单元的形状可以是任意的,但是其对应的物理覆盖是唯一的.

图1 数值流形方法中的覆盖和单元Fig.1 A simple example to illustrate the basic concepts of NMM

1.2 覆盖位移函数

数值流形方法中数学覆盖独立于物理网格，因此一般常用的有限元网格总可以被引入到数值流形方法中.这些有限元网格必须足够大来覆盖整个问题区域.为了使权函数的建立更加简单，程序实现更加容易，在二维数值流形方法中通常采用三角形或者是四边形网格.如图1所示，数值流形方法中采用规则四边形网格的数学覆盖，双线性的四边形有限元形函数作为数学覆盖的权函数.

这些覆盖函数通过定义在数学覆盖上的权函数wi(x,y)连接在一起

在整个材料体上总体位移函数可以表示为

1.3 数值流形方法模拟不连续问题

数值流形方法模拟不连续问题时裂纹尖端存在奇异性，由于多项式不能准确描述裂纹尖端的应力场，往往会造成求解精度差的问题.这一问题可以通过将附加函数加入到覆盖函数中来解决.如图2所示，含有裂纹尖端的数学覆盖M1,M2,M3和M4各自形成一个物理覆盖，这些物理覆盖称之为奇异的物理覆盖(singular physical cover)[28].这些物理覆盖的覆盖函数通过加入附加函数来考虑不连续尖端场的影响

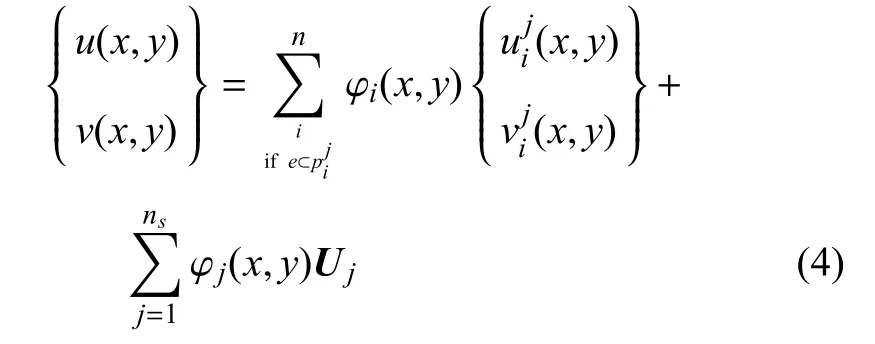
式中Uj为奇异物理覆盖的附加函数

式中，cj为附加函数的未知量矩阵，ns为裂纹尖端所在单元的奇异物理覆盖的数量.Φ为奇异矩阵的基函数矩阵，可以表示为

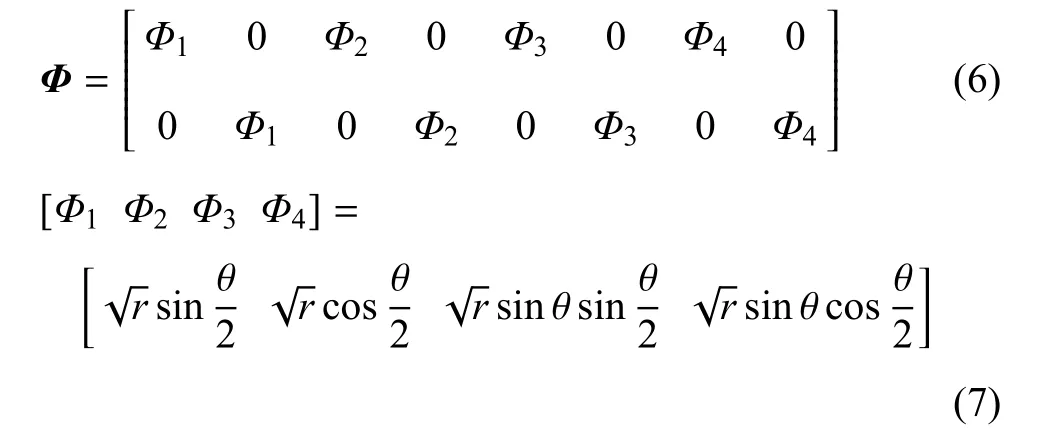
式中，(r,θ)为裂纹尖端局部坐标系中的坐标，r是任意一点到裂纹尖端的距离，θ是裂纹扩展角.基于这种强化方法，裂纹尖端可落在流形单元的任意位置.即使在相对粗糙的数学网格中，我们也可以精确地得到应力强度因子.

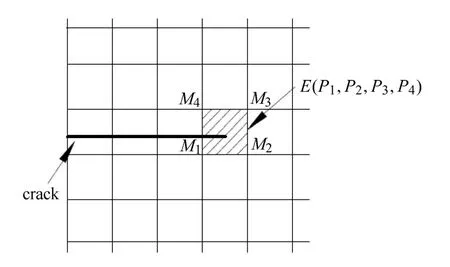
图2 裂纹尖端处的奇异物理覆盖Fig.2 Singular physical covers at crack tip in NMM

2 T样条

2.1T样条基函数

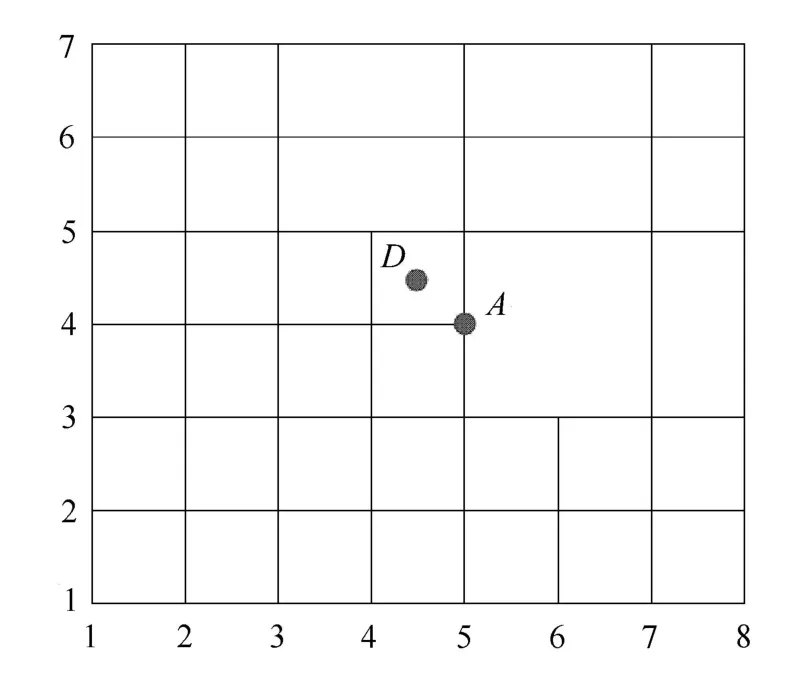
图3 一个T网格Fig.3 A T-mesh

T样条基函数是由其自身的局部节点向量定义的，这些节点向量是从T网格中推导出来的.T样条基函数的局部节点向量按照以下规则确定：当阶次p为奇数时，先将锚点位置所代表的节点值存入局部向量中，然后再分别沿锚点的上下左右4个方向，由锚点位置出发，记录遇到的(p+1)/2个正交边并将每一条正交边对应的节点值存入相应的局部向量中；当p为偶数时，分别沿锚点的上下左右4个方向，由锚点位置出发，直到遇到(p/2+1)个正交边，将每一条正交边对应的节点值存入相应的局部向量中.如图3中的锚点A，当p=1时，其对应的局部向量为ui=[u4,u5,u8]和vi=[v3,v4,v5]，该基函数的支撑域(support)见图4.当p=2时，矩形中心点D为一锚点，相应基函数的局部向量为ui=[u3,u4,u5,u8]和vi=[v3,v4,v5,v6]，其支撑域见图5.

对于一个给定的T网格和阶次p，利用上述过程确定T样条局部向量ui和vi之后，T样条基函数Ti(u,v)可定义为

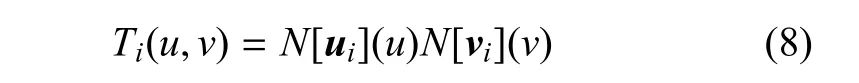
其中N[ui](u)和N[vi](v)可由Cox-de Boor[29-30]递推公式导出

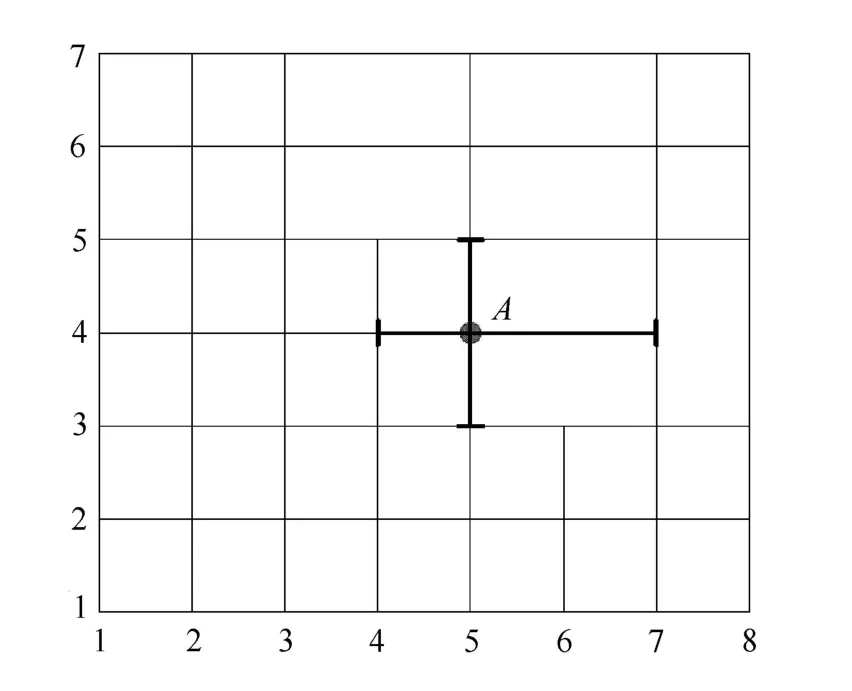
图4 锚点A对应的局部节点向量Fig.4 Inferring local vectors for anchorA

图5 锚点D对应的局部节点向量Fig.5 Inferring local vectors for anchorD

2.2T结点扩展

一个T结点扩展是一条线段，通常包括一个面扩展和一个边扩展.从T结点自身出发沿着它缺失的那一个方向进行延长直到于第[(p+1)/2]个正交边相交所形成的延长线段即为T结点的面扩展，而T结点的线扩展是从T结点沿着相反的方向出发直到于第[p/2]个正交边相交所经历的线段.p为T样条的阶次，[(p+1)/2]和[p/2]为分别对(p+1)/2和p/2取整.称两个T节点扩展是相交的，如果它们相交于一个都在它们内部的点；称两个T结点扩展是接触的，如果它们相交于一点，并且该点为它们至少一个的端点.如图6所示，点虚线为T网格中T结点的面扩展，线段虚线为T结点的线扩展.可以看出T结点A和T结点C的扩展是相交的，T结点A和T结点B的扩展是接触的.当把所有的T结点扩展加入到T网格中后，T网格变为扩展的T网格，记作Text.

2.3 适合分析的T样条

适合分析的 T样条 (analysis-suitable T-spline，AST)定义在一个限制的T网格上，即T网格中不存在竖直的T结点扩展与水平的T结点扩展相交或接触的情况.AST样条继承了T样条所有重要的数学特性而且具有高效的局部细分性.AST样条基函数具有以下重要性质：

图6 扩展T网格Fig.6 The extended T-mesh.Face extensions are represented by dotted arrows and edge extensions are represented by dashed arrows.The T-junctions are denoted by black dots

(1)单位分解性,即

(2)非负性

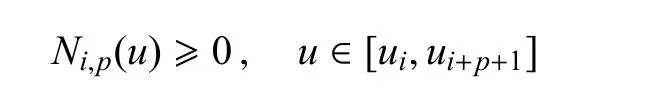
(3)线性无关性

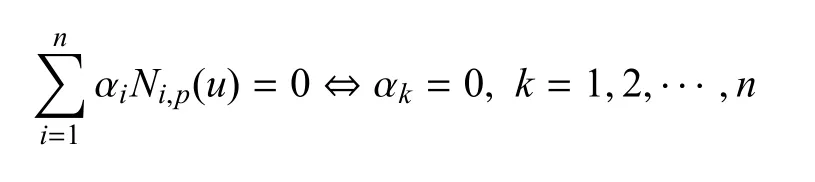
(4)紧支性

图7(a)中所示的T网格是适合分析的，因为在相应的Text不存在竖直的T结点扩展与水平的T结点扩展相交或接触的情况.

3 基于AST样条基函数的高阶数值流形方法

高阶位移函数的构造可通过提高权函数的阶次来实现，这种方法往往需要沿单元边界配置适当的边内节点，这些结点的出现增加了前处理的复杂性，特别是对于大型复杂的空间问题.本节提出采用AST样条基函数来构造数值流形方法中的权函数，有效地避免了该问题的出现.

图7 (a)适合分析的T网格(b)扩展T网格Fig.7(a)An analysis-suitable T-mesh(b)the extended T-mesh

在数值流形方法中，采用如图8所示的T网格作为数学覆盖系统，图中黑色圆点为T样条基函数的锚点，在此表示一个数学覆盖的位置.当p=1，2和3时，T网格中不存在竖直的T结点扩展与水平的T结点扩展相交或接触的情况，所以此T网格产生的T样条为AST样条.将AST样条的基函数作为数值流形方法中的权函数，数学覆盖的构造形式及范围可按3.2节中T样条基函数的相应规则进行确定.以右侧裂纹尖端所在单元为例，当T样条基函数的阶次为1时，如图9(a)所示紧邻的4个矩形网格形成一个数学覆盖，流形单元为相应的4个数学覆盖形成的物理覆盖的重叠区域.当T样条基函数的阶次为2时，如图9(b)所示紧邻的9个矩形网格形成一个数学覆盖，流形单元为相应的9个数学覆盖形成的物理覆盖的重叠区域.类似的，当T样条基函数的阶次为3时，如图9(c)所示紧邻的16个矩形网格形成一个数学覆盖，流形单元为相应的16个数学覆盖形成的物理覆盖的重叠区域.

p=1时，{x1,x2,x3}和{y1,y2,y3}分别为x,y方向的单调不减的实数序列，对应的权函数可通过式(1),式(2)和式(9)推导，权函数可以表示为

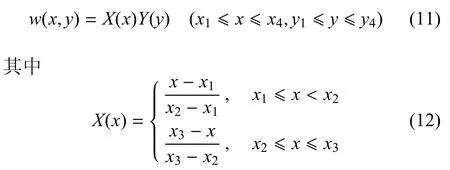
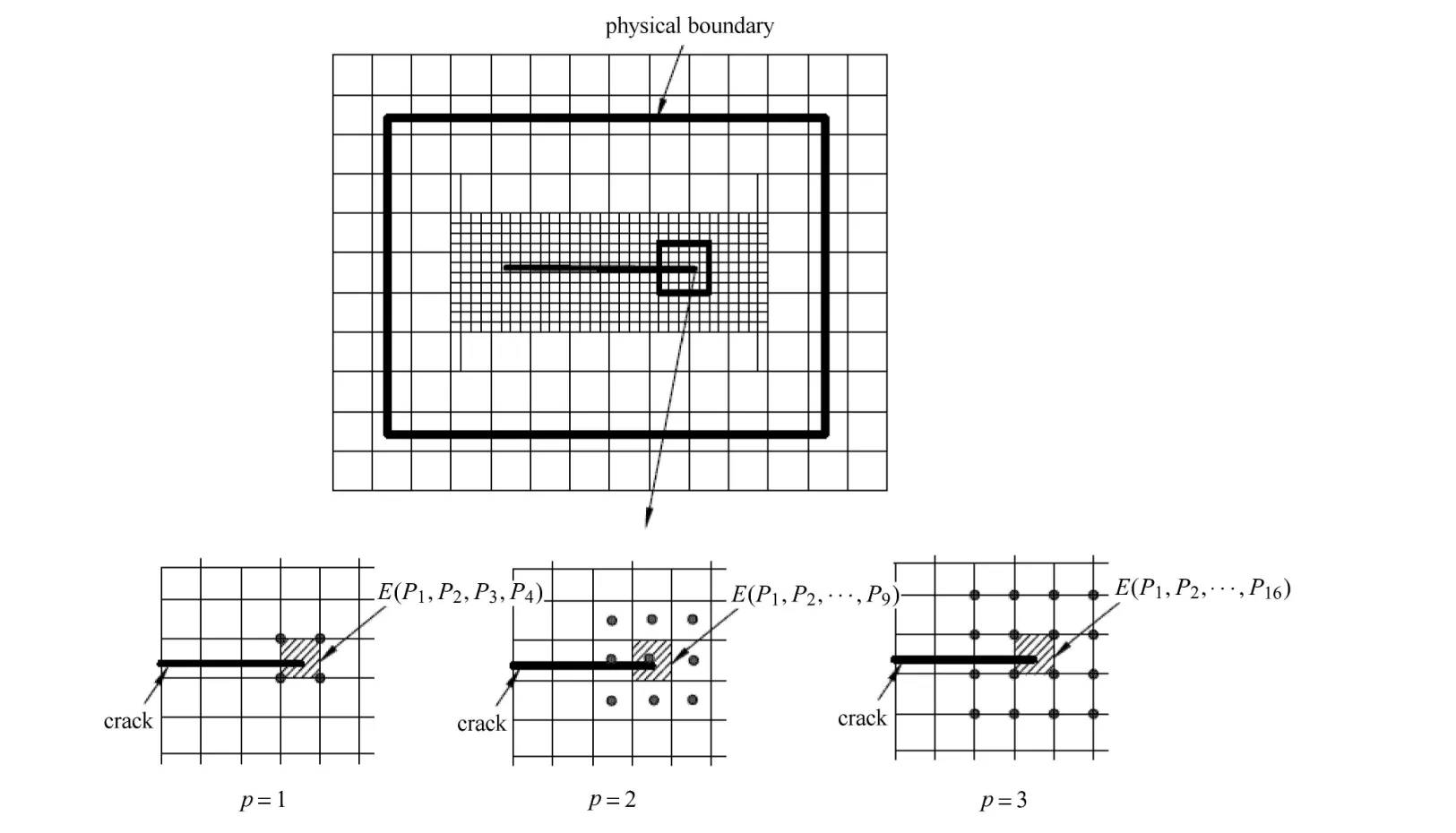
图8 采用AST网格的数值流形方法Fig.8 Numerical manifold method with AST mesh

图9 不同阶次的数学覆盖Fig.9 Mathematical cover with dif f erent order

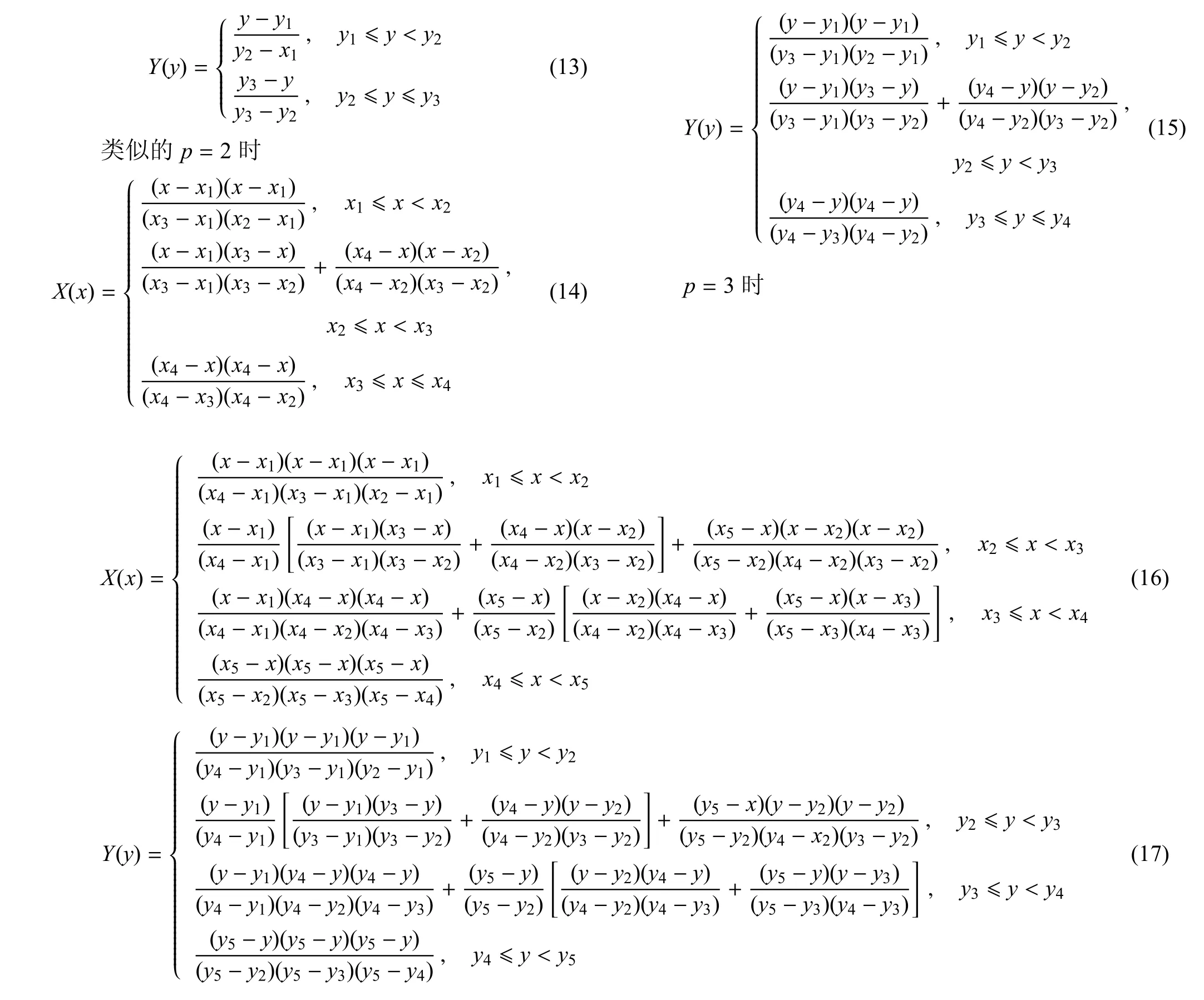
基于AST样条建立的数值流形方法，权函数具有AST样条基函数的重要性质，满足数值流形方法中对权函数的要求.此外，权函数具有Cp-1连续性，权值在3种不同阶次数学覆盖区域中的分布见图10～图12.需要指出的是，当T网格中不存在T结点且阶次为1时，AST基函数等价于一阶Lagrange插值函数.

图10 p=1时权值在一个数学覆盖中的分布Fig.10 Distribution of weights in a mathematical cover whenp=1

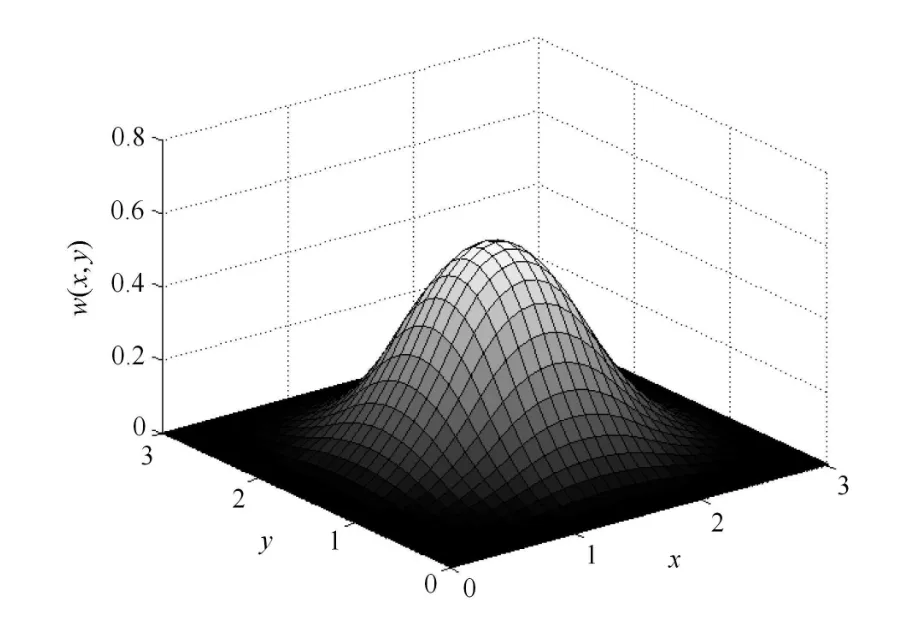
图11 p=2时权值在一个数学覆盖中的分布Fig.11 Distribution of weights in a mathematical cover whenp=2

图12 p=3时权值在一个数学覆盖中的分布Fig.12 Distribution of weights in a mathematical cover whenp=3

4 数值算例

4.1 Timoshenko悬臂梁

悬臂梁模型如图13所示，左侧为固定端，右侧施加剪切分布力P=1.模型参数：D=1，L=5；平面应变问题，杨氏模量E=1000，泊松比v=0.该问题的解析解为

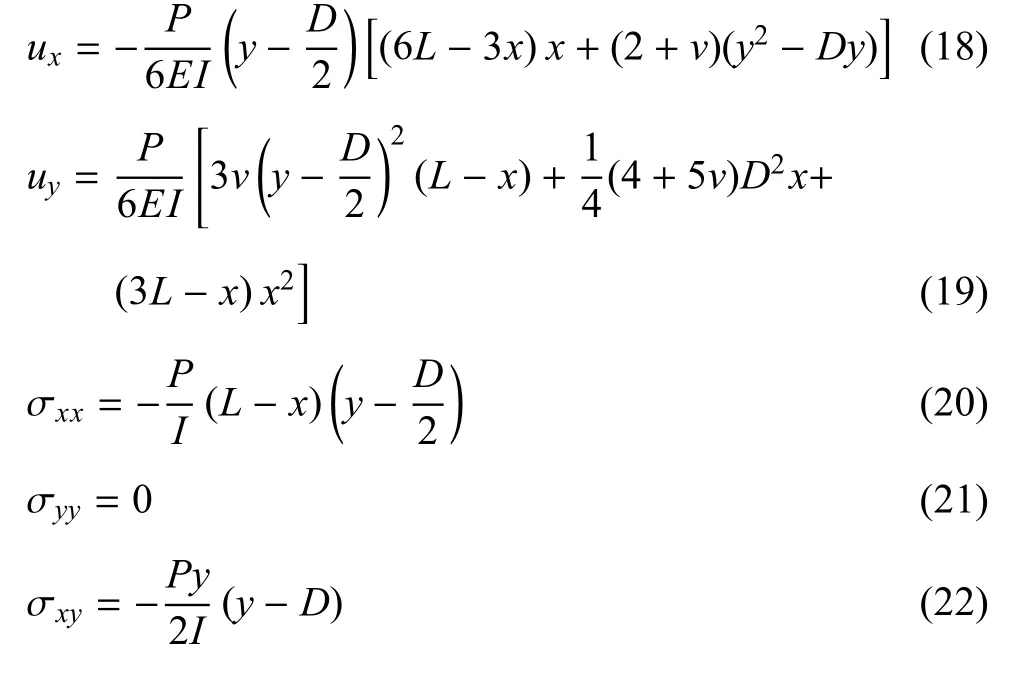
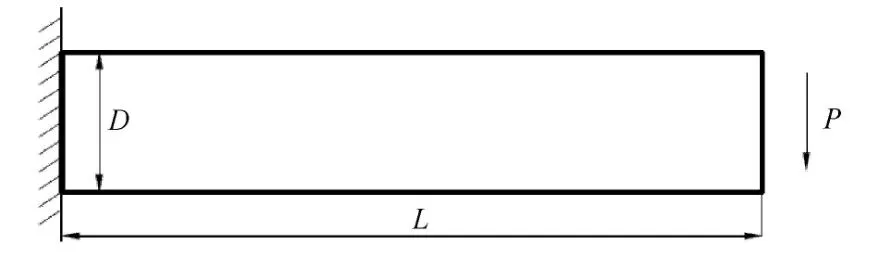
图13 Timoshenko悬臂梁Fig.13 Timoshenko cantilever beam

采用如图14所示的T网格作为数值流形方法中的数学覆盖系统，由于网格中不存在T结点，故T网格是适合分析的.分别采用不同阶次(p=1,2,3)的AST样条基函数构造数值流形方法中数学覆盖的权函数.

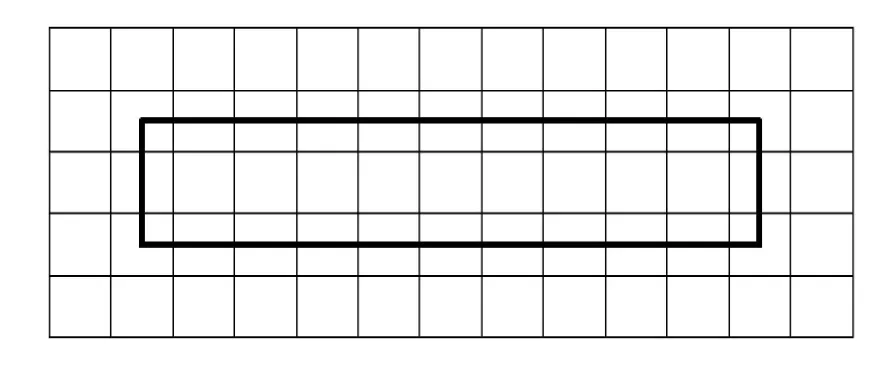
图14 数学覆盖网格图Fig.14 Mathematical covers

图15和图16分别给出了悬臂梁底边(y=0)位移及应力随位置的变化图.从图中可看出：当采用一次T样条基函数时，数值流形方法(NMM based on linear AST-spline，NMM_T1)的计算结果与解析解存在一定的计算误差；采用高阶次的 T样条基函数后，相应的高阶数值流形方法(NMM based on quadratic AST-spline，NMM T2；NMM based on cubic AST-spline，NMM_T3)与解析解吻合得很好.

图17为不同密度T网格下，悬臂梁应变能的计算误差.应变能的计算误差定义为

其中U为应变能的理论解，Uh为数值流形方法的求解结果.从图中可以随着T网格的加密，基于3种不同阶次AST基函数的数值流形方法均是收敛的，但收敛速度随着AST基函数的阶次提高不断增大.

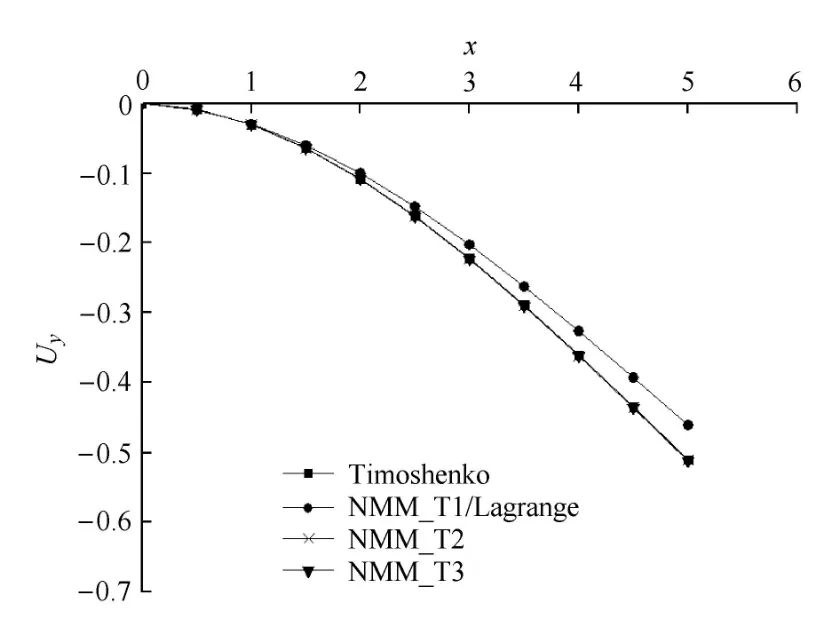
图15 y=0时y方向位移变化图Fig.15ydisplacement versus position wheny=0

图16 y=0时σx变化图Fig.16 σxversus position wheny=0

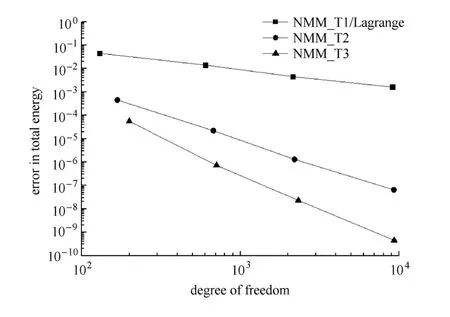
图17 悬臂梁应变能误差Fig.17 Error in strain energy of the cantilever beam

4.2 含中心边裂纹的有限板受单向拉伸

如图18所示有限矩形板，中部有一条长度为a的边裂纹，矩形板单向受力σ=4，长2h=3，宽b=1.此问题的理论解可以表示为

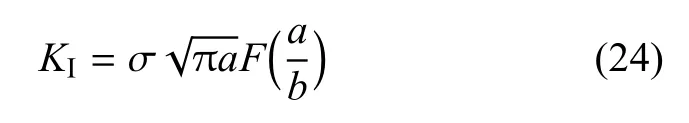
式中

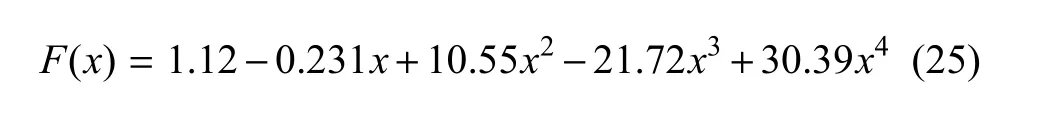
图18 含单边裂纹的有限板Fig.18 Finite plate with crack

图19 数学覆盖网格加密Fig.19 Mathematical mesh refinemen

取不同裂纹长度a，利用相互作用积分法[31]计算不同裂纹长度下裂纹强度因子 (stress intensity factors，SIFs).采用图19所示的两种数学加密网格,(a)为针对裂纹区域的数学网格全局加密，(b)为针对裂纹区域的局部加密.裂纹强度因子的计算结果见表1～表3.图20和图21分别为两种不同加密策略下裂纹强度因子的计算误差.对比可以得出：局部加密策略要比全局加密策略更有优势，即在计算精度基本一致的情况下采用局部加密数学网格的自由度要小于全局加密数学网格的自由度；在相同数学覆盖网格下，随着AST样条基函数阶次的提高，裂纹强度因子的计算误差在逐步减小.

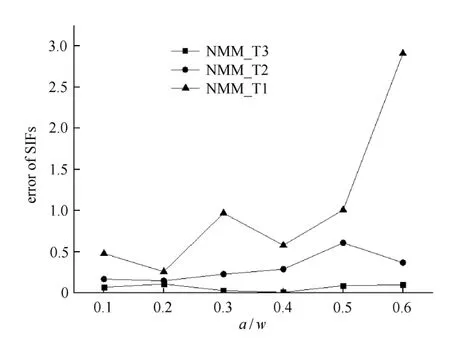
图20 全局数学网格加密时裂纹强度因子的计算误差Fig.20 Error of SIFs using global refinemen mesh

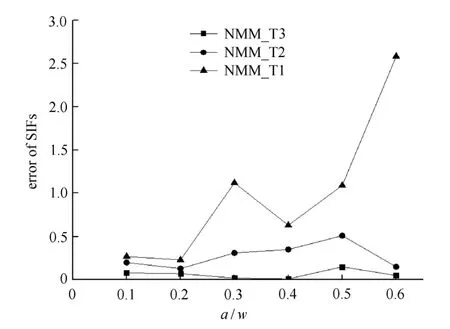
图21 局部数学网格加密时裂纹强度因子的计算误差Fig.21 Error of SIFs using local refinemen mesh

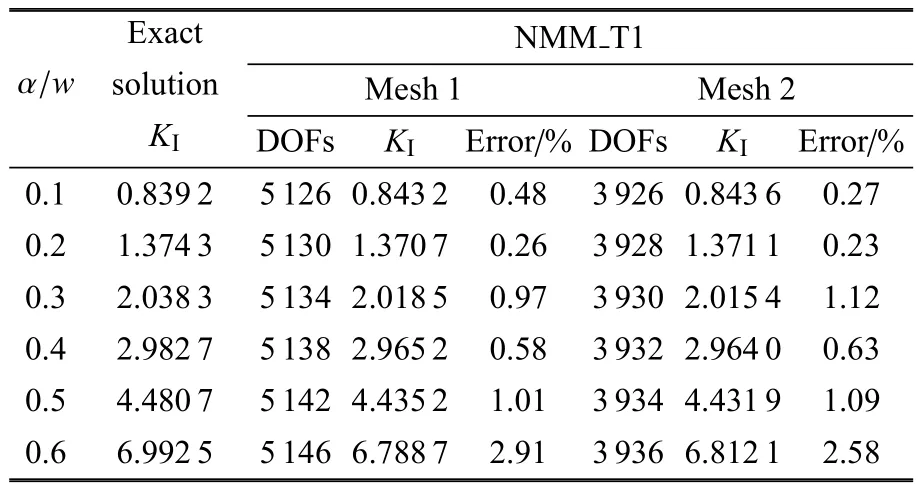
表1 采用一次AST样条数值流形方法计算结果Table 1 SIFs results for NMMT1

表2 采用二次AST样条数值流形方法计算结果Table 2 SIFs results for NMMT2

表3 采用三次AST样条数值流形方法计算结果Table 3 SIFs results for NMMT3

5 结论

本文将AST样条引入到数值流形方法中，通过提高AST样条基函数的阶次及改变相应的数学覆盖的形式，建立了高阶数值流形方法的分析格式.AST样条基函数具有线性无关，单位分解，局部加密等许多重要性质，使其非常适合用于工程设计及分析.文中将AST基函数取代传统的Lagrange插值函数来建立数值流形方法中的权函数，在建立高阶数值流形方法的分析格式的同时，实现了数学网格的局部加密.算例结果表明：随着AST样条基函数阶次的提高，数值流形方法的计算结果有了明显的改善；基于AST样条基函数的数值流形方法在保持计算精度的前提下降低了自由度的数量.

文中仅列举了3种不同阶次的AST样条，我们仍可通过提高AST样条基函数阶次及改变相应的数学覆盖形式建立更高阶次的数值流形方法.在引入AST样条思想之后，数值流形方法中数学覆盖的局部加密变得更加容易，更自然.

1 Shi GH.Manifold method//The 1st Int.Forum on DDA Simulation of Discontinuous Media.Bekerley,California,USA.1996：52-204

2 石根华,裴觉民.数值流形方法与非连续变形分析.北京：清华大学出版社,1997(Shi Genhua,Pei Juemin.Numerical ManifoldMethod and Discontinue Deformation Analysis.Beijing：Tsinghua University Press,1997(in Chinese))

3 Tal Y,Hatzor YH,Feng XT.An improved numerical manifold method for simulation of sequential excavation in fractured rocks.International Journal of Rock Mechanics and Mining Sciences, 2014,65：116-128

4 焦健,乔春生,徐干成.开挖模拟在数值流形方法中的实现.岩土力学,2010,31(9)：2951-2957(Jiao Jian,Qiao Chunsheng,Xu Gancheng.Simulation of excavation in numerical manifold method.Rock and Soil Mechanics,2010,31(9)：2951-2957(in Chinese))

5 朱爱军,邓安富,曾祥勇.数值流形方法对岩土工程开挖卸荷问题的模拟.岩土力学,2006,27(2)：179-183(Zhu Aijun,Deng Anfu, Zeng Xiangyong.Numerical manifold method for simulation of excavation unloading in geotechnical engineering.Rock and Soil Mechanics,2006,27(2)：179-183(in Chinese))

6 姜清辉，王书法.锚固岩体的三维数值流形方法.岩石力学与工程学报，2006，25(3)：528-532(Jiang Qinghui,Wang Shufa.Three dimensional numerical manifold method simulation of anchor bolt supported rock mass.Chinese Journal of Rock Mechanics and Engineering，2006,25(3)：528-532(in Chinese))

7 Wei W,Jiang QH,Peng J.New rock bolt model and numerical implementation in numerical manifold method.International Journal of Geomechanics2016,E4016004

8 王水林,葛修润.流形方法在模拟裂纹扩展中的应用.岩石力学与工程学报,1997,16(5)：405-410(Wang Shuilin,Ge Xiuyun.Application of manifold method in simulating crack propagation.Chinese Journal of Rock Mechanics and Engineering,1997,16(5)：405-410 (in Chinese))

9 Chiou YJ,Lee YM,Tesay RJ.Mix mode fracture propagation by manifold method.International Journal of Fracture,2002,114：327-347

10 Wu ZJ,Wong LNY.Friction crack initiation and propagation analysis using the numerical manifold method.Computers&Geotechnics,2012,39：38-53

11 Yang SK,Ma GW,Ren XH,et al.Cover refinemen of numerical manifold for crack propagation simulation.Engineering Analysis with Boundary Elements,2014,43：37-49

12 Yang YT,Tang XH,Zheng H.Three-dimensional fracture propagation with numerical manifold method.Engineering Analysis with Boundary Elements,2016,72：65-77

13 Jiang QH，Deng SS，Zhou CB.Modeling unconfine seepage fl w using three-dimensionalnumericalmanifold method.Journalof Hydrodynamics，2010，22(4)：554-561

14 姜清辉,邓书申,周创兵.三维高阶数值流形方法研究.岩土力学,2006,27(9)：1471-1474(Jiang Qinghui,Deng Shushen,Zhou Chuangbing.Study of three-dimensional high-order numerical manifold method.Rock and Soil Mechanics,2006,27(9)：1471-1474(in Chinese))

15 苏海东,崔建华,谢小玲.高阶数值流形方法的初应力公式.计算力学学报,2010,27(2)：270-274(Su Haidong,Cui Jianhua,Xie Xiaoling.Initial stress equation for high-order manifold method.Chinese Journal of Computational Mechanics,2010,27(2)：270-274(in Chinese))

16 苏海东.固定网格的数值流形方法研究.力学学报,2011,43(1)：169-178(Su Haidong.Study on numerical manifold method with fi ed meshs.Chinese Journal of Theoretical and Applied Mechanics,2011,43(1)：169-178(in Chinese))

17 Wang Y,Hu MS,Zhou QL,et al.A nes second-order numerical manifold method model with an efficient scheme for analyzing free surface fl w with inner drains.Applied Mathematical Modelling, 2016,40：1427-1445

18 Zheng H,Xu DD.New strategies for some issues of numerical manifold method in simulation of crack propagation.International Journal for Numerical Methods in Engineering,2014,97：986-1010

19 郭朝旭,郑宏.高阶数值流形方法中线性相关问题的研究.工程力学,2012,29(12)：228-232(Guo Chaoxu,Zheng Hong.Study of linear dependence problem in high-order numerical manifold method.Engineering Mechanics,2012,29(12)：228-232(in Chinese))

20 蔡永昌,刘高扬.基于独立覆盖的高阶数值流形方法.同济大学学报(自然科学版),2015,43(12)：1794-1799(Cai Yongchang, Liu Gaoyang.High-order manifold method with independent covers.Journal of Tongji University:Natural Science,2015,43(12)：1794-1799(in Chinese))

21 Fan H,Zheng H,He SM,et al.A novel numerical manifold with derivative degrees of freedom and without linear dependence.Engineering Analysis with Boundary Elements,2016,64：19-37

22 Hughes TJR,Cottrell JA,Bazilevs Y.et al.Isogeometric analysis：CAD,finit elements,NURBS,exact geometry,and mesh refine ment.Computer Methods in Applied Mechanics and Engineering, 2005,194：4135-4195

23 Piegl L,Tiller W.The NURBS Book.Springer-Verlag Berlin and Heidelberg GmbH,Berlin,1997：292-295

24 Sederberg TW,Zheng J,Bakenov A,et al.T-splines and T-nurccs.ACM Transactions on Graphic,2003,22：477-484

25 Bazilevs Y,Calo VM,Cottrell JA,et al.Isogeometric analysis using T-splines.Computer Methods in Applied Mechanics and Engineering,2010,199：229-263

26 Zhang YL,Liu DX,Tan F.Numerical manifold method based on isogeometric analysis.Science China Technological Sciences,2015, 58：1520-1532

27 Li X,Zheng J,Sederberg TW,et al.On linear independence of T-splines blending functions.Computer Aided Geometric Design, 2012,29：63-76

28 Ma GW,An XM,Zhang HH,et al.Modelling complex crack problems using the numerical manifold method.International Journal of Fracture,2009,156：21-35

29 Cox MG.The numerical evaluation of B-Splines.IMA Journal of Applied Mathematics,1972,10：134-149

30 Carl DB.On calculating with B-Splines.Journal of Approximation Theory,1972,6：50-62

31 Sukumar N,Huang ZY,Prevost JH,et al.Partition of unity enrichment for bimaterial interface cracks.International Journal for Numerical Methods in Engineering,2004,59：1075-1102

HIGHER-ORDER NUMERICAL MANIFOLD METHOD BASED ON ANALYSIS-SUITABLE T-SPLINE1)

Liu Dengxue∗,†,2)Zhang Youliang∗Liu Gaomin∗,†

∗(State Key Laboratory of Geomechanics and Geotechnical Engineering，Institute of Rock and Soil Mechanics，Chinese Academy of Sciences，Wuhan430071，China)

†(University of Chinese Academy of Sciences，Beijing100049，China)

Numerical manifold method(NMM)is a very fl xible numerical method which contains and combines finit element method(FEM)and discontinuous deformation analysis(DDA).High-order numerical manifold method can be constructed by increasing the order of the weight function.This method often needs to configur the appropriate edge nodes along the element boundary,the emergence of these nodes increase the complexity of pre-processing,especially for large and complex spatial problems.On the other hand,the level of approximation of NMM can be improved by splitting the elements into smaller ones(known as h-refinement)With regard to the h-refinement a cover refinemen strategy is necessary to overcome the singularity of the stress when simulating crack propagation in NMM.One traditional solution is to refin the entire mesh which can lead to a significan decrease in the computational efficiency.In this paper analysis-suitable T-spline is introduced into NMM and regular rectangular meshes are used as the mathematical cover system. Specificall,analysis-suitable T-spline is linearly independent,forms a partition of unity,and can be locally refine which make it meet the demands of both design and analysis.The basis function of analysis-suitable T-spline is adopted as the weight function in NMM to construct high-order NMM and make the local refinemen for feasible adaptive procedure. Two numerical examples are given to demonstrate the accuracy and efficiency of the proposed method and the results show that the higher order AS T-spline based NMM shows higher accuracies when solving both continuous and discontinuous problems.Furthermore,the local mesh refinemen using analysis-suitable T-spline reduces the number of degrees of freedom while maintaining calculation accuracy at the same time.

high-order numerical manifold method，linear independence，analysis-suitable T-spline，local refinemen

O302

A doi：10.6052/0459-1879-16-217

2016-08-01收稿，2016-11-17录用,2016-11-23网络版发表.

1)国家重点基础研究发展计划(973计划)(2014CB047100)和国家自然科学基金(11272330)资助项目.

2)刘登学，在读博士，主要研究方向：计算岩石力学.E-mail：liudengxue123@sina.cn

刘登学,张友良,刘高敏.基于适合分析T样条的高阶数值流形方法.力学学报,2017,49(1)：212-222

Liu Dengxue,Zhang Youliang,Liu Gaomin.High-order numerical manifold method based on analysis-suitable T-spline.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1)：212-222