气井不同生产条件下液滴曳力系数变化规律探讨

钟华国，邹翔，蒋玉勇，郭风军，张沂，李志敏



气井不同生产条件下液滴曳力系数变化规律探讨

钟华国1，邹翔2，蒋玉勇2，郭风军2，张沂2，李志敏2

（1. 长庆油田分公司第六采气厂， 陕西 西安 710018； 2. 长庆油田分公司第一采气厂， 陕西 西安 710018）

曳力系数是推导临界流速公式的重要参数，为保证临界流速公式的准确性，应对曳力系数的取值及其发展规律进行分析。本文对液滴曳力系数的计算公式进行了对比优选，并以苏里格气田实际气井作为研究对象，计算其在不同产量、压力和气液比条件下的曳力系数值，从而得到该系数的规律性认识，以便在实际的现场操作中，预判气井随开发过程中临界流速变化趋势，精确计算不同气井临界流速，准确判断井底积液。

气井；曳力系数；液滴模型

随着气田开发，气井积液比例逐渐增大，准确预测气井的临界携液流速，对于优化气井工作制度和排除井底积液具有十分重要的意义。目前主要使用的有Turner（1969）提出的圆球模型[1]、李闽（2001）的椭球模型[2]及王毅忠（2007）的球帽模型[3]。

三个模型认为当液滴重力等于所受浮力、曳力之和时，液滴将悬浮于井筒中。若气流能将气井中最大液滴带出井口，井筒能连续携液生产。

通过对三个模型进行公式变换，可得液滴临界携液流速公式为：

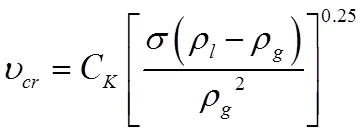
因此，对曳力系数在不同生产条件下的变化规律进行准确认识，结合不同气井生产条件的差异性，通过计算Cd值得到相应的临界携液流速，对于准确判断研究气田气井连续携液能力有着积极作用。

1 曳力系数计算公式、确定及优选

1.1 Cd计算公式

当一个球体与流体之前存在相对运动时，球体受到的作用力称为曳力。当相对运动的雷诺数较小时（Re<0.1），Stokes(1851)[4]发现球体受到的曳力仅与粘性项有关。当雷诺数Re=700~20 000时，Newton（1710）[5]发现曳力仅与惯性项有关，得到Cd为0.44。Oseen[6]于1910年近似地考虑了惯性项， 得到：

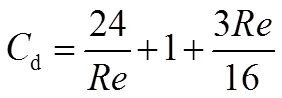
曳力系数在以往研究中主要通过标准曳力曲线来确定。该曲线表现的是经过大量实验得到的单个刚性球体在静止、等温、不可压缩及无限大流场的流体中作匀速运动时的Cd与Re之间的关系。

从曲线中可出Cd随Re的变化无规律可循，为满足石油化工设计需要，科学家们采用经验关联式的方法进行分段拟合或全域拟合[7]，该拟合方法主要适用于对视为刚性球体的液滴计算。

目前，分段拟合主要以Clift. R和White两人建立的关联式为主。全域拟合关联式以Brauer（1972）[8]和Clift & Gauvin（1970）[9]相对较好，邵明望（1994）[10]采用非线性拟合的方法整理出一个新的全域拟合关联式。

1.2 Cd计算公式优选

利用计算机编程，对全域拟合的三种关联式、分段拟合的两种关联式进行计算，并将计算结果与实验数据进行对比。可知，分段拟合公式精度高于全域拟合公式，其中White分段拟合公式明显优于其他四种关联式。

1.3 Cd的误差修正

液滴的曳力系数主要与液滴形状和雷诺数相关。当气井中气液相对速度差较小时，液滴近似保持球状，此时应用刚性球体关联式计算气流对液滴的曳力时误差不大；当气液相对速度差较大，液滴变形较大时，使用刚性球体关联式计算气流对液滴的曳力时存在较大的误差[13]。

Helenbrook[15]提出式（8）来修正这种影响，并由式（8）可知当Re较高时，液滴内部流动对曳力系数的影响不可忽略。

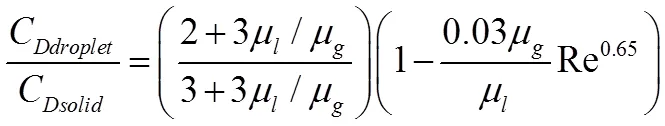
2 苏里格气田气井不同条件下Cd及其规律认识

苏里格气田目前单井日均产气1.0×104m3/d。具有气藏埋藏较深、单井产气量较小、气井普遍产液的特点，单井平均气水比介于9 000~25 000 m3/m3。本文结合苏里格气田矿场数据模拟实际气井。

运用计算机编程的手段，采用White分段拟合公式并结合式（7），对实际气井条件下的Cd值进行定量计算并绘制定不同压力、产量、气液比情况下的下Cd值的变化规律曲线。

由图1可知，在气井定产量下，Cd值计算结果的范围约为0.265 3～0.484 0。曳力系数随压力的变化可分为三种情况：1）气井在产量＜1.0×104m3/d时，Cd随着井口压力的增大缓慢下降；2）当1.0×104m3/d＜＜5.0×104m3/ d时，Cd值随着井口压力的增大逐渐增大，于10～12 MPa左右时，Cd值增大趋势平缓；3）气井在产量＞5.0×104m3/ d时，Cd随着井口压力的增大，值均为0.44左右。

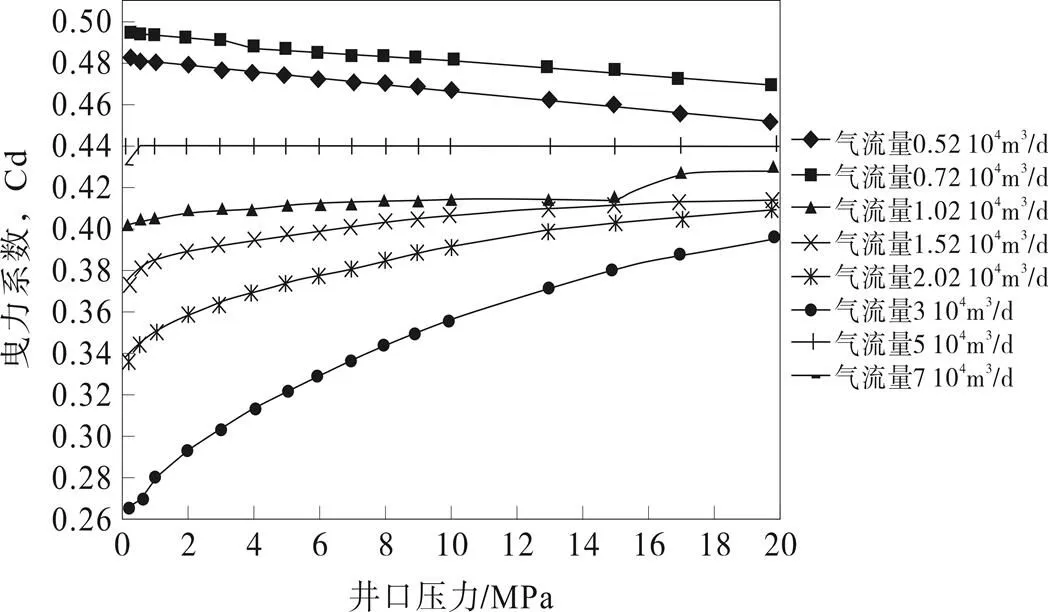
图1 不同气体流量下Cd值变化曲线

由图2可知，当气井定气液比的情况下，曳力系数随井口压力的增大呈上升趋势，当井口压力达到10~12 MPa时，不同气液下的曳力系数增长曲线基本重合，即当井口压力较大时，不同气液比下的Cd值基本一致。

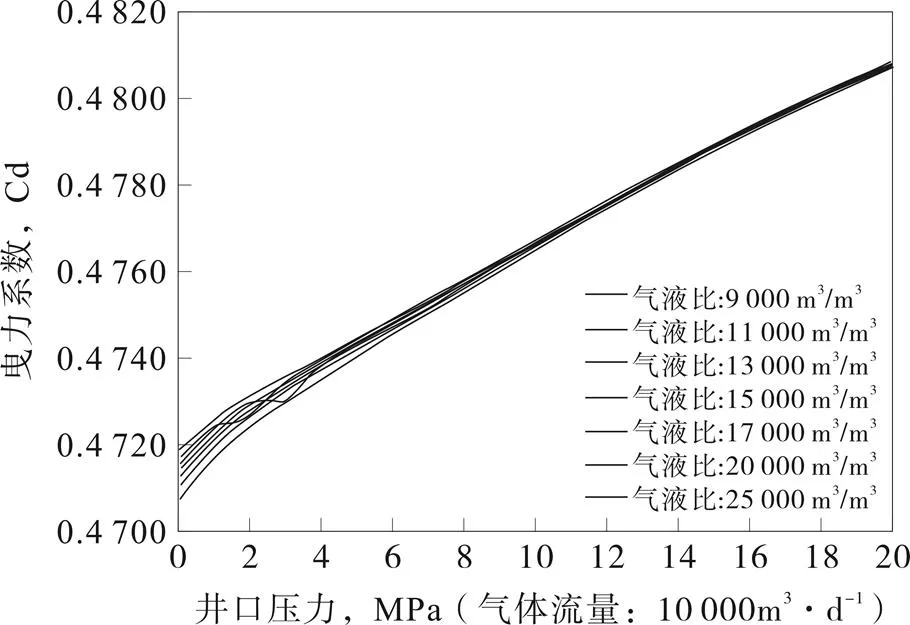
图2 Cd值随井口压力的变化曲线（q=1×104 m3/d）

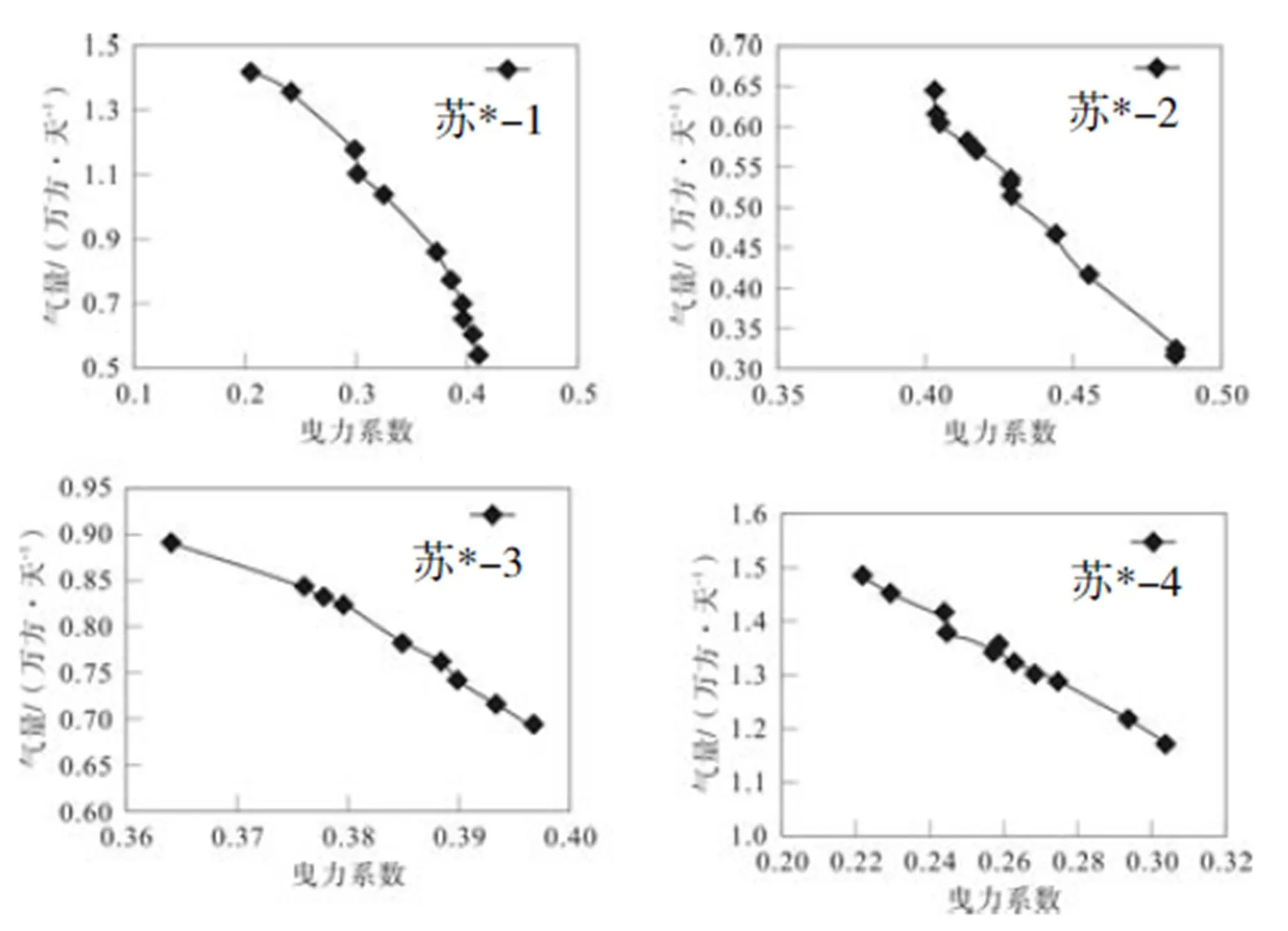
图3 Cd值随产量的变化曲线

由图3可知，当气井定压力的情况下，选取苏*-1，苏*-2，苏*-3，苏*-4四口井的生产数据，这四口井属于连续生产井，油压、套压变化很小，油套压差稳定，随着产气量的增加，气相流速增加，雷诺数增大。结合曳力系数公式与标准曳力曲线可知，曳力系数随着产气量的增大而减小。

3 实例验证

利用式（1）对苏里格气田实际气井进行了临界携液流速计算，并预测气井的生产状态。计算时取天然气相对密度0.601 2，气井井口压力根据实测数据，采气管柱内径0.062 m，产出液密度为1 074 kg/m3，表面张力取0.06 N/m。实例计算结果如表1。

此模型是根据气井的实际气井参数计算出雷诺数，根据优选曳力系数计算式计算Cd值，再利用临界携液流量模型计算出的临界流速。预测结果与实际生产较一致。因此，用White分段拟合公式计算的曳力系数来修订Turner模型的临界流量算法，可以提高预测苏里格气井积液精度。

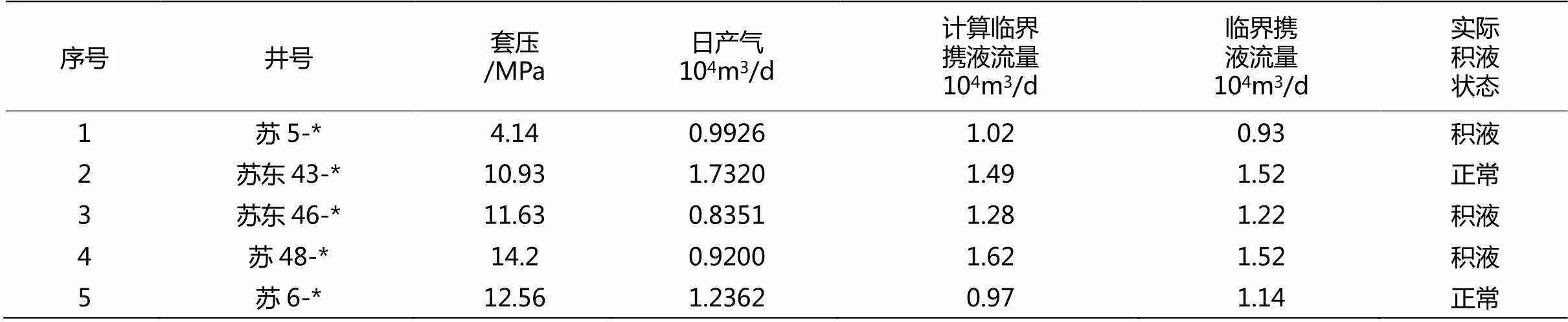
表1 气井临界携液流量计算结果

4 结 论

（1）对于自由降落的液滴，其韦伯数存在临界值20～30，在临界值以下的液滴为不变形破裂的圆球形。在此前提下，假设液滴为球形颗粒可保证气井在临界产量计算值下正常携液生产。所以，高气液比条件下液滴存在形式视为拟圆球形颗粒是合理的。

（2）通过对三种全域拟合关联式和两种分段拟合关联式的计算值与实验值对比，优选出精度较高的White分段拟合关联式，并进行实例计算，验证了其提升精度的可能性。

（3）在气井定产量下，曳力系数随压力的变化可分为三种情况：

（a）气井在产量＜1.0×104m3/d时，Cd随着井口压力的增大缓慢下降；

（b）当1.0×104m3/ d＜＜5.0×104m3/d时，Cd值随着井口压力的增大逐渐增大，于10～12 MPa左右时，Cd值增大趋势平缓；

（c）气井在产量＞5.0×104m3/d时，Cd随着井口压力的增大，值均为0.44左右；

（4）气井在定气液比的情况下，曳力系数随井口压力的增大呈上升趋势，当井口压力达到10~12 MPa时，不同气液下的曳力系数基本一致，即气液比在井口压力较小时对Cd值的变化有一定影响，但随着井口压力的逐渐增大，气液比对Cd值的影响逐渐减小。

（5）气井在定压力的情况下，曳力系数随着产气量的增大而减小。

[1] Turner R G. Analysis and Prediction of Minimum Flow Raft for the Continuous Removal of Liquids from Gas Wells [J]. JPT，1969：75-82.

[2] 李闽，郭平，谭光天.气井携液新观点[J]. 石油勘探与开发，2001，28 (5)：105-106.

[3] 王毅忠，刘庆文. 计算气井最小携液临界流量的新方法[J]. 2007，26（6）：82-85.

[4] Stokes，G.G.，Trans. Cambridge Philosophical Society，Vol.1851，9 (2)：8.

[5] Newton，I.，“Principia Mathematica，”Book Ⅱ，Scholium to Proposition XL，1687.

[6] 化学工程手册. 第5卷第20篇，化学工业出版社，1989：1815-1816.

[7] 魏纳，孟英峰，等. 天然气井连续携液液滴曳力系数研究[J]. 天然气技术，2007，1（6）：50-51.

[8] Brauer，H.，and Mewes，D.，Chem. Ing. Tech. 1972，44：865-868.

[9] Clift，R.，and Gauvin，W. H.，Proc. Chemeca，1970，70：114-28.

[10] 邵明望. 球形颗粒沉降阻力系数拟合关联式[J]. 化工设计，1994 (3) ：16-18.

[11] R.Clift，J.R.Grace and M.E.Weber. Bubbles，Drops and Particles. 1978：1815.

[12] White，B.R.，in Encyclopedia of Fluid Mechanics，Vol.4：Solids and Gas-Solids Flow，N. P. Cheremisi-noff(ed.)，Gulf Publishing D Company， Houston， 1985.

[13] 王志彬，李颖川. 气井连续携液机理[J]. 石油学报，2012，33 (4)：681-686.

[14] Liu Z，Reitz R D. An analysis of the distortion of the distortion and breakup mechanisms of high speed liquid drops [J]. Int. J. Multiphase Flow，1997，23(4)：631-650.

[15] Helenbrook B T，Edwards C F. Quasi-steady deformation and drag of uncontaminated liquid drops[J]. Int. J. Multiphase Flow，2002，28(10)：1631-1650.

Research on the Drag Coefficient of Liquid Droplet in Gas WellsUnder Different Production Conditions

1,2,JIANG Yu-yong,GUO Feng-jun,ZHANG Yi,LI Zhi-min

（1. NO.6 Gas production Plant of PetroChina Changqing Oilfield Company, Shaanxi Xi'an 710018, China； 2. NO.1 Gas production Plant of PetroChina Changqing Oilfield Company, Shaanxi Xi'an 710018, China）

Drag coefficient is one of the important parameters for deriving the critical flow velocity formula. In order to guarantee the accuracy of derived critical flow velocity formula, drag coefficient value and its development law should be analyzed. In this paper, taking actual gas wells in Sulige gas field as research object, the calculation formula of droplet drag coefficient were compared and optimized for calculation of droplet drag coefficient under different conditions of output, pressure and gas-liquid ratio, so as to obtain the regularity understanding of the coefficient.

gas well；drag coefficient；liquid-drop model

钟华国（1973-），男，采气高级技师，毕业于西南石油大学石油工程专业，从事采气工艺方面研究工作。

2017-11-17

TE377

A

1004-0935（2017）12-1190-03