低复杂度GMSK线性接收机的设计与实现
莫明威
(中国西南电子技术研究所,成都 610036)
【信息科学与控制工程】
低复杂度GMSK线性接收机的设计与实现
莫明威
(中国西南电子技术研究所,成都 610036)
通过基于GMSK信号的Laurent分解,提出了一种低复杂度GMSK线性接收算法,利用卫星GMSK信号的主要信号能量成分的表达式可等效为经过成型滤波的正交调制信号,设计出了低复杂度GMSK线性接收机,并对所提出的接收机进行了性能损失的理论分析。基于FPGA芯片对提出的接收机进行了硬件实现,实测结果表明,接收机的误码率性能相对于理论误码率性能的损失小于1 dB,所提出的接收机已应用于我国的探月工程任务中。
卫星信号;线性接收机;Laurent分解;GMSK解调
近几年来,航天测控、遥感卫星等系统对星地链路的数据传输速率越来越高,随着空间在轨卫星数量的快速增加,可用的射频频段变得越来越拥挤。为此,国际空间数据系统咨询委员会(consultative committee for space data systems,CCSDS)提出在未来的近地和深空探测任务中使用具有更高带宽效率的GMSK调制[1]。
NASA和ESA从20世纪末就开始对包括GMSK调制在内的多种高带宽效率调制技术进行了全面的研究[2-3],并且已经应用于近几年的航天测控任务中[4]。我国的航天测控系统采用的调制方式具有带外衰减慢和频谱利用率低的缺点,迫切需要采用高带宽效率的调制方式。
GMSK信号的解调分为非相干和相干解调两大类。文献[5-6]提出了一种非相干解调方案,实现简单但解调损失较大,文献[7]基于相位状态网格图中的相位转移规律提出了一种改进的非相干解调维特比算法,降低了非相干解调损失,但是非相干解调无法跟踪载波多普勒,无法对航天器测速。文献[8]基于GMSK信号的状态变化规律,提出了基于Viterbi算法的MLSE检测,取得了很好的误码率性能,但是算法复杂度高,难以进行工程实现。文献[9]基于GMSK 信号的Laurent分解,通过忽略能量占比小的分解项,极大简化了需要检测的状态,但并未提出获得相干载波的方法。文献[4]分析了GMSK信号的两种载波同步电路的性能,但未给出接收机模型。
为了解决GMSK信号解调复杂度高的问题,本文基于GMSK信号的Laurent分解,设计并实现了一种低复杂度GMSK线性接收机。本文提出的GMSK接收机采用相干解调方式,兼具实现复杂度低和解调性能优良的特点。
1 GMSK信号的Laurent分解
GMSK是一种调制指数h=0.5的部分响应CPM调制,其信号形式为
s(t)=Re{S(t)ei(2πfCt+θ)}
(1)
其中:S(t)为GMSK复基带信号;fC为载波频率;θ为载波初相。Laurent提出将CPM信号的复包络分解为多个调幅脉冲(AMP)的叠加[10],针对调制指数h=0.5的GMSK信号,其复基带信号可以表示为
(2)
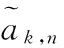
C0(t)=sinψ(t)×sinψ(t+Tb)×
sinψ(t+2Tb)×sinψ(t+3Tb)
(3)
其中,0≤t≤5Tb
(4)
(5)
(6)
(7)
BTb表示高斯滤波器的3 dB带宽与一个发送比特的持续时间的乘积,Q(x)表示高斯概率积分。
根据式(2),GMSK复基带信号包含2L-1个AMP波形,其中第一个AMP波形C0(t)包含主要的信号能量。例如,当BTb=0.5和L=4时,第一个AMP波形C0(t)包含总信号能量的99.1944%。
2 低复杂度GMSK线性接收机的设计
GMSK复基带信号的各个AMP波形分量中,第一个AMP波形占了绝大部分信号能量,从降低设计复杂度的角度考虑,将GMSK复基带信号近似为只包含单个AMP波形的形式,即
(8)
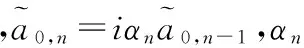
(9)
根据式(9),GMSK信号可以近似看成是一种I、Q支路的符号存在Tb延迟的正交调制信号,且其符号经过成型滤波器C0(t),相应的接收机可以采用正交解调方式,经过载波和符号同步后,对其进行匹配滤波,匹配滤波器与成型滤波器C0(t)一致。
对比式(2)和式(8),可看出GMSK复基带信号由近似前的非线性表示变为近似后的线性表示,因此基于式(8)设计的GMSK接收机是一种线性接收机,极大地降低了接收机的设计复杂度。
GMSK信号在调制时需要经过高斯滤波器,导致发送符号的有效时间被展宽,从而引入符号间干扰(ISI),高斯滤波器的BTb值越小,引入的ISI越严重,因此在接收机设计中需要进行符号均衡。
下面分析采用GMSK信号的近似表达式带来的性能损失。根据式(8),GMSK接收机的接收信号R(t)可以表示为

(10)
其中,N(t)是均值为零,方差为σ2的复高斯白噪声,则接收信号R(t)的信噪比为
SNRin=Eb/(Tbσ2)
(11)
接收信号R(t)经过同相、正交支路的匹配滤波器后,得到同相、正交两路符号:
(12)
(13)
其中,
(14)
(15)
根据式(12)和式(13)可知,接收机仅对GMSK信号的第一个AMP波形进行匹配滤波,使得其余AMP波形经过匹配滤波后的输出成为噪声的一部分,这部分增加的噪声即为aI(m)和aQ(m)表达式中的第二项,这将导致信噪比损失。GMSK信号经过匹配滤波器后,输出的信噪比可近似为
(16)
因此,本研究提出的接收机中采用GMSK信号的近似表达式带来的性能损失为
(17)
3 低复杂度GMSK线性接收机的实现
本研究提出的低复杂度GMSK线性接收机的实现框图如图1。

图1 低复杂度GMSK线性接收机的实现框图
GMSK接收机中的载波同步模块采用COSTAS锁相环实现,其鉴相公式为
e(kTb)=sign[I(kTb)]×Q(kTb)-
sign[Q((k+1)Tb)]×I((k+1)Tb)
(18)
其中,I(kTb)、Q(kTb)分别表示COSTAS锁相环中的同相、正交支路的符号。GMSK信号经过载波同步模块后,输出载波剥离后的GMSK基带信号。
符号同步模块采用迟早门实现,迟门的积分时刻滞后符号同步时钟Tb/4,早门的积分时刻超前符号同步时钟Tb/4。
匹配滤波前需要将载波剥离后的GMSK基带信号的采样率转换为与符号时钟同步的四倍符号速率,采样率转换模块利用积分清零滤波器实现,清零脉冲为符号同步模块产生的四倍符号同步脉冲。
匹配滤波器的系数是通过对C0(t)的波形以四倍符号速率采样得到的。根据式(3),C0(t)的有效时间宽度为5Tb,以四倍符号速率采样得到一个20阶的FIR滤波器。
符号均衡是为了减少ISI,其选取与BTb值有关,当BTb<0.5时,进行符号均衡,当BTb≥0.5时,不进行符号均衡,实现时采用维纳均衡滤波器[11]。
4 实现结果及性能分析
4.1 硬件资源使用情况
基于Altera公司的StratixⅡ系列可编程门阵列(FPGA)芯片EP2S180,对提出的低复杂度GMSK线性接收机进行了硬件实现,硬件资源使用情况如表1所示。从表1可以看出,硬件资源占用率最高的是DSP,达到了DSP总数的26.6%,而寄存器、查找表和BRAM资源的占用率较小。
相对于常规的卫星接收机,本研究提出的接收机仅需增加额外的匹配滤波器、维纳均衡器即可实现GMSK信号的相干解调,其中匹配滤波器采用20阶的FIR滤波器实现,维纳均衡器采用2阶的FIR滤波器实现,只需占用少量硬件资源。

表1 低复杂度GMSK线性接收机的硬件资源使用情况
4.2 解调信号眼图分析
针对CCSDS标准推荐的应用于近地和深空探测的BTb=0.5和0.25两种GMSK信号,经过本文提出的低复杂度GMSK线性接收机解调后,在匹配滤波器输出的信号眼图如图2和图3,针对BTb=0.25的GMSK信号还需经过符号均衡,均衡后的信号眼图如图4。
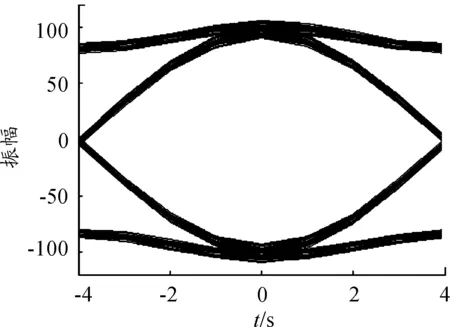
图2 BTb=0.5时匹配滤波器输出的信号眼图

图3 BTb=0.25时匹配滤波器输出的信号眼图

图4 BTb=0.25时符号均衡输出的信号眼图
对比图2和图3可知,BTb=0.5的信号眼图比BTb=0.25的张开幅度大,这是由于BTb=0.25的信号经过的高斯滤波器带宽更窄,导致ISI更严重所造成的。
对比图3和图4可知,经过符号均衡后的BTb=0.25的信号眼图比均衡之前的张开幅度大,可见符号均衡有效地降低了ISI。GMSK信号在经过的高斯滤波器时,由于高斯滤波器的冲击响应持续时间为当前符号的正负若干个符号间隔,因此当前符号的冲击响应会叠加到相邻符号内,而相邻符号的冲击响应也会叠加到当前符号内,从而导致了符号之间互相干扰。符号均衡通过将当前符号减去经过加权后的相邻符号,使得相邻符号在当前符号内的叠加影响减弱,经过符号均衡后的符号更接近实际发送的符号,因此对应的眼图张得更大。
4.3 实测误码率性能分析
本文在高斯白噪声信道下,对符号速率为20 Mbps,BTb=0.25和0.5的GMSK信号进行了误码率测试,测试结果如图5所示,图5中画出了理论误码率曲线作为对比。由图5可知,BTb=0.25,Eb/N0=10.5 dB时,本文提出的接收机的误码率为1e-5;BTb=0.5,Eb/N0=10.0 dB时,误码率为1e-5。根据图5中的理论误码率曲线,误码率为1e-5时对应的Eb/N0理论值为9.6 dB,因此本文提出的接收机误码率性能相对于理论误码率性能的损失小于1 dB。BTb=0.5对应的误码率曲线在BTb=0.25对应的误码率曲线下方,这是由于BTb=0.5的GMSK信号的ISI小于BTb=0.25,从而使得在相同的Eb/N0下,BTb=0.5时接收机的误码率性能优于BTb=0.25。

图5 低复杂度GMSK线性接收机的误码率测试结果
5 结论
基于GMSK信号的Laurent分解,推导了GMSK信号的近似正交调制表达式,并提出了低复杂度GMSK线性接收机。通过硬件实现和误码率性能实测表明,提出的低复杂度GMSK线性接收机误码率性能相对于理论误码率性能的损失小于1 dB,适合应用于近地和深空探测任务。
[1] Bandwidth-Efficient Modulations:Summary of Definition,Implementation,and Performance[R].CCSDS 413.0-G-1 Green Book,2003.
[2] MARTIN W,YAN T Y,GRAY A,et al.CCSDS-SFCG Efficient Modulation Methods Study at NASA/JPL-Phase 4:Interference Susceptibility[C].Netherlands,1999.
[3] SESSLER G M A,ABELLO R,JAMES N,et al.GMSK demodulator implementation for ESA deep-space missions[J].Proceedings of the IEEE,2007,95(11):2132-2141.
[4] SHAMBAYATI S,LEE D K.GMSK modulation for deep space applications[C]//Aerospace Conference,2012 IEEE.IEEE,2012:1-13.
[5] 张梦瑶,张有志.一种π/4-DQPSK和GMSK调制可变信号一体化解调技术[J].无线电工程,2015,45(2):30-33.
[6] 吴玉成,陈 亮,李国权.GMSK中频数字化非相干接收机的设计与实现[J].无线电工程,2008,38(3):58-60.
[7] 吴伟仁,节德刚,丁兴文,等.深空测控通信中GMSK体制非相干解调算法研究[J].宇航学报,2014,35(12):1437-1443.
[8] 曾佐祺,李赞.基于Viterbi算法的GMSK信号解调性能分析与仿真[J].重庆邮电大学学报,2008,20(2):132-138.
[9] KALEH G K.Simple coherent receivers for partial response continuous phase modulation[J].IEEE Journal on Selected Areas in Communications,1989,7(9):1427-1436.
[10]LAURENT P.Exact and approximate construction of digital phase modulations by superposition of amplitude modulated pulses (AMP)[J].IEEE transactions on communications,1986,34(2):150-160.
[11]RICE M.Digital communications:a discrete-time approach[M].Pearson Education India,2009.
(责任编辑 杨继森)
Design and Implementation of Low Complexity GMSK Linear Receiver
MO Ming-wei
(Southwest China Institute of Electronic Technology, Chengdu 610036, China)
A low complexity GMSK linear receiver algorithm based on the Laurent decomposition of GMSK signals was proposed. The new algorithm utilized the main signal energy component of satellite GMSK signal which is equivalent to shaping quadrature modulation signal to design a low complexity GMSK linear receiver, and the theoretical performance loss of the proposed receiver was analyzed. The receiver proposed was realized in FPGA, and the BER performance test showed that the BER performance losses was less than 1dB comparing with the theoretical BER performance. The proposed receiver has been used in China’s lunar exploration mission.
satellite signal; linear receiver; Laurent decomposition; GMSK demodulation
2016-09-23;
2016-10-25
莫明威(1986—),男,硕士,工程师,主要从事卫星信号处理研究。
10.11809/scbgxb2017.02.023
莫明威.低复杂度GMSK线性接收机的设计与实现[J].兵器装备工程学报,2017(2):101-104.
format:MO Ming-wei.Design and Implementation of Low Complexity GMSK Linear Receiver[J].Journal of Ordnance Equipment Engineering,2017(2):104-104.
TN911.72
A
2096-2304(2017)02-0101-04

