动态称量技术在发射药称重过程中的应用

伍凌川，李全俊，黄 权

(中国兵器工业第五八研究所弹药中心，四川 绵阳 621000)

【信息科学与控制工程】

动态称量技术在发射药称重过程中的应用

伍凌川，李全俊，黄 权

(中国兵器工业第五八研究所弹药中心，四川 绵阳 621000)

为了提高弹药发射药装药生产过程中发射药称量的精度和速度，设计一种改进型的动态称重系统，采用粗-中-细3级给料方式，建立发射药动态称重系统数学模型，通过称重信号处理和称重给料控制算法克服现有模式存在的效率低、精度不高等缺陷；200次的发射药称量试验，都稳定在7.0±0.1g范围内，表明改进后的称重系统满足弹药生产过程中发射药快速精确称量的需求。

动态称量；发射药称重；弹药生产

在弹药自动装药装配生产中的发射药称装是保证弹药产品生产品质和效率的关键工序，高效、高精的称量过程是弹药产品发射药称装环节的最基本要求。如何采用电子信息、自动控制以及计算机分析等技术提高称量系统的精度和速度是实现提高发射药称量过程工艺的关键所在。在实际弹药生产线上，操作人员希望发射药称量与产品压制同步进行，压弹过程中同时完成，即与压弹过程同步，实现零停机。因此，必须在保证正常生产的同时完成发射药的连续和快速称量；通过动态称重技术可以基本实现称量与压制的同步工作，满足这一要求，其主要特征：

1) 称量物品不是静止状态。测量时，被称重的弹药发射药处于某种运动或持续振动等情况，并处于带有冲击力的状态下；

2) 称量的外部环境也处于运动状态，即称重衡器放置于自身处于运动或振动的机床台面或机架等支撑体上；

3) 称重数据读取时间短而快，时间一般低于称重衡器的稳定时间。

要实现快速连续、准确的装药称量，得到称量的稳态值，就需要对由称重传感器、信号采集与处理系统组成的动态称重系统进行正确的描述和分析，同时减小动态称量的不稳定性，降低称量响应时间，对耦合分量间进行解耦，实现发射药的动态补偿。

发射药动态称重系统的难点是称量精度和速度相互匹配和兼顾；系统同时受到时变、非线性、不确定性以及随机干扰等因素影响。当发射药输送速度较快时，发射药颗粒对称量衡器产生冲击并形成振动，影响称量的精度。为满足称量精度，就需要降低传输的速度。弹药生产时发射药高精度和高速度的动态称量是弹药生产领域的一大难题。为此，研究在弹药装药中将动态控制与测量方法相互融合，实现优势互补，从而在较高的效率中实现发射药称重过程的动态高精度称量。

1 发射药动态称重系统组成及原理

弹药发射药称重过程有其特殊性，需要为其专门制定动态称量方案。发射药动态称量的特殊性主要体现在以下几个方面：

1) 称量物体为发射药，属于一种不规则的颗粒状物体，对精度要求高，系统绝对精度要达到0.1 g左右；

2) 对安全性的要求相当高，系统设计必须符合安全性要求；

3) 要求系统响应速度迅速，必须满足生产节拍要求，尽量提高生产效率。

由于以上特殊性，对发射药动态称量高精度给料的实现造成极大的困难。因此，必须设计一套高效率的响应快速、测量精度高的控制系统，对生产线上的称量系统和给料系统进行协调控制，其组成如图1所示。

图1 组合式发射药称量系统示意图

相对以往采用的粗-细两级给料方式，作者采用粗-中-细3级给料；两级给料采用的是传统的快加药和慢加药相结合的加药原理。由于在实现过程中发现：快速过程给料冲击大，慢速过程给料速度慢，直接导致发射药称重精度和效率无法提高，成为弹药生产过程中影响效率和品质的瓶颈环节。而3级给料采用的是组合式加药原理和机理，通过增加一次中速加药降低了粗加药时的物料冲击，减少了细加药的时间，从而提高了发射药称重加药控制精度，降低了发射药装填加药时间。

3级给料工作过程如下：控制系统发送指令，发射药按粗-中-细3个速度依次向计量药斗投料，控制系统实时读取计量药斗的重量和发射药的重量，控制粗-中-细3个装药料斗的开关，具体过程如下：

1) 发射药重量远小于所设定的重量时(一般为小于70%)，粗药斗打开快速下料，其余药斗关闭；

2) 发射药重量在设定重量的70%～90%时，中药斗以中间速度下料，其余药斗关闭；

3) 发射药重量达到设定重量90%以上时，细药斗打开，下料速度缓慢，保证最终的称量精度。

4) 发射药重量快达到设定重量时，细药斗马上关闭。因为空中还有一部分发射药的重量，以及执行机构电磁阀有延时，一般需要一个提前关闭的落差量，即对加药时间进行预估。

其理想状态给料曲线如图2所示，大、中投量决定称量的速度，小投量决定称量的精度。

图2 理想状态给料曲线

2 发射药动态称量技术

建立的数学模型和控制算法同时适用于两级和3级给料称量方式，但是3级给料的控制原理和信号计算过程更复杂，参数取样更丰富，模型更加接近于实际，称量精度更高，同时兼顾了称量效率。

2.1 发射药动态称重系统数学模型的建立

典型的发射药动态称重系统模型如图3所示，可以等效为一个二阶系统，模型由质量块、弹簧和阻尼器构成，其动态模型为

(1)

式(1)中：m为称重药斗质量，K为弹簧弹性系数，C为等效阻尼常数，f(t)为被称发射药的重量，g(t)为发射药的冲击力，x(t) 称重药斗相对于参考零点的位移。

在式(1)中，g(t)物料冲力受发射药下落的高度和速度影响，而发射药动态称量系统实际称量时在刚开始开启粗给料斗时冲击力较大，但是粗给料加药的精度对最终的称量精度不产生影响，同时冲击力造成的称量过冲量在称量后期可通过称量系统自动调整过来，至此g(t)可以忽略，从而式(1)能简化变化为

(2)

式(2)中，当称重药斗质量m不发生改变时，此模型为典型的二阶时变非线性系统，在此对其进行拉氏变换并转换成标准形式，可得到系统的传递函数为[1]

(3)

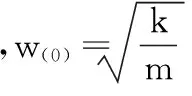
图3 发射药称重系统模型

2.2 发射药动态称重系统控制原理

根据上述分析，发射药动态称重系统为在线实时称量，控制系统读取的发射药重量实时变化。而在实际弹药发射药称量过程中，下料的振动、发射药对衡器的冲击等随机干扰会对发射药的称重精度产生较大影响。在发射药称量非线性模型内，所形成的动态称重数学模型与实际称量会有一定的偏差，从而需要校正，而校正的实现仍较困难；由于模型的阻尼不断变化，这也导致校正或配置极点实施难度较大。为实现发射药的动态定量称量，需要快速并准确的称量出通过给料阀门的发射药质量，及时关闭给料阀门，并且预估已通过给料阀门，尚未落到称重传感器上而处于空中的那部分发射药质量。

在称重信号处理部分，对系统建立含有未知参数的数学模型，根据在线参数估计的基本思想，即系统数学模型结构确定后，实时读取称重系统的输入输出数据，同时按照某种固定的算法连续通过读取的数据去修正模型中的参数估计值，即一边测量数据，一边修正模型[2]。

考虑实际称量中的干扰，仅用式(3)进行模型计算后，其计算值与实际值之间会有很大的误差。为了更加接近实际的称重系统，从而构建了一套含有扰动噪声v(t)的动态校准试验，实现称量系统数学模型尽量接近实际称量系统。扰动噪声主要是观测噪声，没有明显的相关性，可以近似看成是随机噪声[3]。系统控制结构如图4所示。

图4 发射药动态称重控制系统结构

2.3 称重信号算法

发射药动态称重控制系统为PLC，其传递函数以差分方程实现为最佳，这样便于应用递推表达式[4]。输入随机噪声后的系统结构如图5所示。

图5 输出端加入噪声后的结构

根据随机信号处理理论，假设v(k)为随机噪声，其均值为0、方差为σ2并服从正态分布，输入变量为u(k)、输出变量为z(k)，系统为

(4)

式(4)中A(q-1)=1+a1q-1+…+anq-n,B(q-1)=1+b1q-1+…+bnq-n。

通过总体分布类型，为了对其中一个或多个未知参数进行较好的估计，采用极大似然法。目的在于：只要此数学模型输出正确，其称量系统参数一定是得到准确值的最大概率参数，确保系统得到确定参数。为此，本文选用极大似然法对系统模型参数进行估计，构造一个随机观测数据和自变量的似然函数为未知参数θ，当似然函数在某一个参数达到极大时，就得到有关参数的估计值[5]。

输入变量u(k)与输出变量z(k)是相对独立的，依据极大似然法原理，对数据ZN=[z(0),z(2),…,z(N-1)]T寻找似然函数为

(5)

式(5)中，θ=[a1,a2,…,an,b1,b2,…,bn]T，uN=[u(1),u(2),…,u(N)]T。

由式(5)可得，在ZN-1，uN和θ已知条件下，似然函数L(ZN/un,θ)的值取决于v(k)的概率分布，似然函数式(5)进一步转化为

(6)

v(k)为扰动均值为0、方差为σ2、服从正态分布的不相关随机噪声，式(6)可改写为

(7)

为使式(7)的值达到最大，即有

(8)

(9)

将式(9)代入式(6)可得

(10)

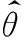
(11)

的值取得最大。

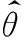
通过分析，随机噪声v(k)以观测噪声的形式出现，即使v(k)不服从正态分布，只要θ的估计值满足式(11)，都可以取得较满意的效果[1]。基于系统模型的通用性，并加入了动态振荡和冲击力干扰，同时过滤了噪声、尖峰干扰等，再进行参数估计并利用结果相互校正。

2.4 称重系统给料控制算法

在对称重信号进行预估处理的基础上，当系统秒重到接近给定值时，控制系统需要提前动作以达到当电磁阀完全关闭时所得到的质量正好等于或者接近于设定的质量。

假设经过预估处理的称量值为P时，停止输送发射药，则最终实际质量为：

Pm=P-Pg+P1

(12)

其中：Pm为称重实际值；P为下料停止时读数；Pg为发射药冲击力；P1为下料停止时滞留在空中的发射药重量。

发射药比重和速度等将影响Pg和P1的数值；当发射药类型和下落速度固定时，Pg和P1的值是基本稳定的。为了使Pm等于或接近设定的目标值，采用逐次逼近法调节P进行逼近[7]。如果A为设定称量值，An是第n次下料停止后实际重量值，Bn是第n次下料停止后称重传感器读数，则第n+1次下料应在称重传感器读为B(n+1)时停止下料：

B(n+1)=Bn+δ1(A-An)+δ2(A-A(n-1))2+

δ3(A-A(n-2))3+…

(13)

δ2,δ3,…，δn近似于0，在实际编程时采用一次逼近算法并省略2次以后的运算，从而简化了计算机的运行。

如果第n次称量称重传感器读数为Cn时，停止下料，经过时间t后，计量药斗基本稳定，读数为Dn，将其视为计量药斗内发射药的实际重量，则第n+1次粗下料停止时C(n+1)为

C(n+1)=Cn+K1×(D-Dn)

(14)

其中：D为粗加药的最佳值，根据实际经验选定；K1为修正系数，根据经验K1=0.5，初始值C1=设定值[8]。

一样的方法，在精加药时对称量值进行修正，从而保证系统称量的最高精度。如果第n次称量，当称重传感器读数为Pn时，精加下料停止，经过时间t后，计量药斗稳定时读数为Qn，将其视为计量药斗内发射药的实际重量，则第n+1次精加药停止时P(n+1)为

P(n+1)=Pn+K2×(Q-Qn)

(15)

其中：Q为设定值；K2为修正系数。

通过实际的大量的称量试验数据和称量后复检数据得出，Qn在允许称量偏差内时，K2=0.2，超标时K2=0.8，初始值P1=设定值。

3 实验分析与验证

在常温条件下，称量7.00 g的粒状发射药，按照系统1 s/次 采集的称重控制器重量，其单次称量的发射药重量曲线如图6所示。

图6 单次称量重量曲线

经过200次的发射药称量试验，从结果中随机抽取20发已称量的发射药，在经过校准的精度为0.001 g电子天平上重新称量并记录重量数据，其称量结果取样柱状对比图如图7。

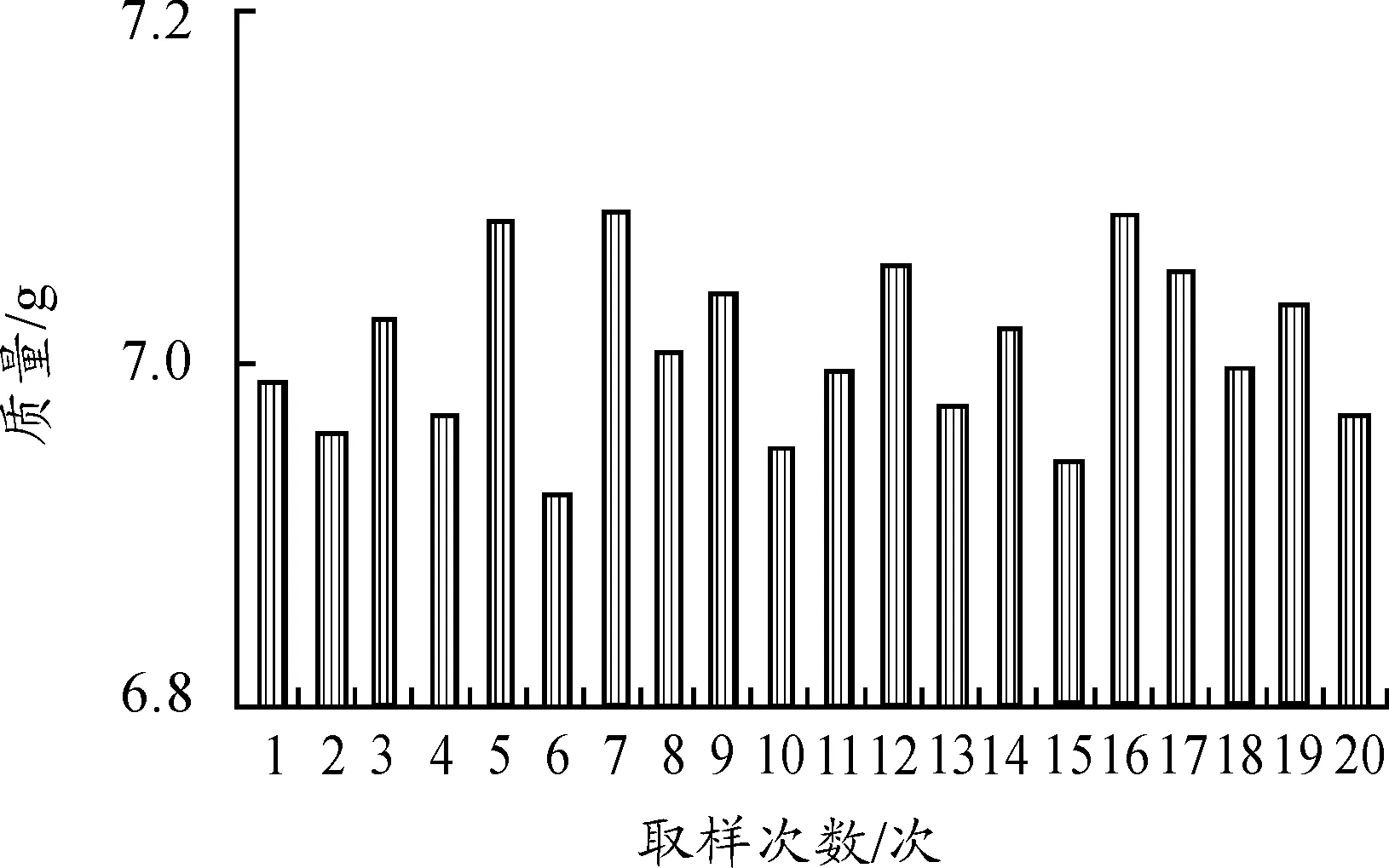
图7 称量结果取样对比

从以上实验数据中得出，图6中的单次发射药重量曲线与图2中的理想给料曲线十分逼近，且称量的发射药重量全都稳定在7.0±0.1g范围内，满足高精度称量的要求。造成波动的原因主要是称量过程中滞空发射药以及发射药下落的高度差所引起的。首先，在进料过程中，发射药从给料装置下落到料斗里，只有到达料斗里的那部分称重传感器才能检测到，而空中的余料是检测不到的，但当排料口打开后，最终得到的发射药实际重量却包括滞空的发射药；其次，发射药下落的高度差由于机械结构是固定的，物料下落的高度随着物料在料斗里的堆积而逐渐减少，造成发射药下落的冲击力产生变化；与此同时，发射药给料速度与下落高度差变化还具有不稳定因素，不能完全精确控制，只能通过称重信号处理算法与给料控制算法逼近真实称量过程。

4 结语

改进型的发射药动态称重系统采用粗-中-细三级给料方式，建立发射药动态称重系统数学模型，通过称重信号处理和称重给料控制算法克服现有模式存在的缺陷。实验结果表明：改进后的称重系统满足弹药生产过程中发射药快速精确称量的需求，但如何精确控制发射药给料速度与预测估计滞空物料重量需要进一步研究。

[1] 杨光伟.定量包装称重控制器的设计与实现[D].大连:大连理工大学,2007.

[2] HALIMIC M,BALACHANDRAN W.Performance Improvement of Dynamic Weighing Systems using Linear Quadratic Gaussian Controller[C]//IMTC 2003-Instrumentation and Measurement Technology Conference,2003:1537-1540.

[3] 吴向峰.动态粒状物料定量称重技术研究[D].北京:中国计量科学研究院,2006.

[4] 胡春海,陈静.用于动态称重的模型参数估计方法[J].自动化仪表,2005,20(4):23-25.

[5] 殳伟群.基于参数估计的动态称重新方法[J].计量学报,1993,14(2):149-153.

[6] GAO Z,MAO J.Dynamic Weighing Technology Combining Parameter Identification[C]//Proceedings of the Third International Symposium on Instrumentation Science and Technology,2004(1):367-371.

[7] 张海青,李宝安.定量下料问题的动态称重解决方案[J].计量学报,1998,19(3):221-224.

[8] 王书鹤.螺旋加料动态定量称重控制方法的研究[J].山东大学学报(自然科学版),2003,38(1):83-85.

(责任编辑 杨继森)

Application of Dynamic Weighing Technology in Propellant Powder Weighing

WU Ling-chuan, LI Quan-jun, HUANG Quan

(Center of Ammunition, No.58 Research Institute of China Ordnance Industries, Mianyang 621000, China)

To improve propellant powder weighing precision and velocity in munition production, we proposed an improved dynamic weighing system, using a III level loading method--coarse powder first, then the medium size and last the fines to establish a mathematical model of dynamic weighing system for propellant powder. The weighing signal processing and loading control algorithm can work against limitations of existing patterns, and in the propellant powder weighing tests for 200 times, the vaule is within 7.0±0.1g, and experiment result shows the improved weighing system can meet the requirement of rapidly precise weighing of propellant in the process of ammunition production.

dynamic weighing; propellant powder weighing; munition production

2016-09-22；

2016-10-29

国家高技术研究发展863计划项目(2014AA041604)

伍凌川(1978—)，男，高级工程师，主要从事弹药装药装配工艺技术研究。

10.11809/scbgxb2017.02.017

伍凌川，李全俊，黄权.动态称量技术在发射药称重过程中的应用[J].兵器装备工程学报，2017(2):70-74.

format:WU Ling-chuan, LI Quan-jun, HUANG Quan.Application of Dynamic Weighing Technology in Propellant Powder Weighing[J].Journal of Ordnance Equipment Engineering,2017(2):70-74.

TP273

A

2096-2304(2017)02-0070-05