基于多项式滤波的常减压装置稳态工况判别
罗 凡,陈夕松,张向荣,梅 彬
(1.南京富岛信息工程有限公司,江苏南京210061;2.东南大学自动化学院,江苏南京210096)
基于多项式滤波的常减压装置稳态工况判别
罗 凡1,2,陈夕松2,张向荣1,梅 彬1
(1.南京富岛信息工程有限公司,江苏南京210061;2.东南大学自动化学院,江苏南京210096)
常减压装置稳态工况判别对于后续工艺的实时优化具有重要意义。目前化工领域多采用固定窗口、分段统计等方法,影响因素多,容易造成误判。文中提出1种基于多项式滤波的稳态判别方法,该方法采用滑动窗口对当前窗口内的数据进行多项式滤波,根据滤波后多项式1次项系数的大小判断装置的稳态与否,滑动窗口的长度可以根据历史稳态数据自适应确定,通过实例分析验证了该方法的有效性。
常减压蒸馏;稳态判别;多项式滤波;滑动窗口
常减压蒸馏装置是炼油加工的第1道工序,通过蒸馏可按产品生产方案将原油分割成相应的直馏汽油、煤油及各种润滑油馏分等半成品。常减压是炼油厂最大的耗能装置之一,占炼油总耗能的25%~30%。通过对常减压装置进行实时优化,可以提高价值产品收率,降低装置的能耗,对企业经济效益的提高具有重要的意义[1]。实际生产过程中,对常减压蒸馏装置进行实时优化前,需要对装置的工况进行稳态检测。
化工领域一般采用统计学方法和手段,如选用均值、标准差、变异系数等统计量,以及直方图、控制图等统计技术,对生产运行进行稳态析[2,3]。一方面,由于抽样的局限性,样本信息不可能是总体信息的完整反映,采用固定窗口或者分段统计的方法,需要操作者根据经验确定窗口大小,对稳态检测结果具有较大的影响。另一方面,在实际工业测量中,测量数据往往包含噪声,若不考虑噪声的干扰,或者仅仅采用传统的1次多项式进行参数拟合,会将一些非斜率变化的信息拟合到1次项中,造成错误地判断数据在变化的假象,影响稳态判别[4]。这些因素导致传统方法难以满足炼化企业对常减压稳态判别的实时性和精准性的要求[5]。
针对传统方法存在的不足,提出1种多项式滤波稳态检测方法,稳态检测时,对当前测量点所处的窗口中的数据进行多项式滤波,得到反映该窗口内数据变化特征的曲线,根据曲线的趋势特征来确定测量信号是否处于稳态。窗口的长度可以根据历史稳态数据自适应地确定,相比较根据经验确定窗口的大小,前者对稳态检测影响的结果较小。在窗口滑动的过程中,测量数据可以被多次利用,提高了稳态检测的准确性。
1 稳态检测方法
1.1 多项式滤波
在实际测量中,测量值中含有噪声的影响因素。为了减少噪声对测量值的干扰,可以采用多项式滤波的方法。多项式滤波能从测量信号中除去噪声部分,从而留下反映基本趋势的部分。
多项式滤波实际上是基于多项式回归模型的信号处理方法[6,7]。信号x(t)可以表示为时间t的函数,见(1)式:

式中 m—模型阶数;p0—窗口内的均值大小;p1—变量随时间变化的快慢,p2—斜率变化的快慢。
令 θ=[p0p1…pm]T为模型的参数向量,r(t)=[p0p1…pm]T为回归变量,则(1)式模型简记为(2)式:

测量信号x~=[x~(1),…,x~(n)]T在已知的情况下,应用最小二乘法可以得到参数θ的最优估计,见(3)式:

通过(3)式估计的多项式滤波参数,可以得到处于观测窗口内的测量数据的趋势曲线,见(4)式:
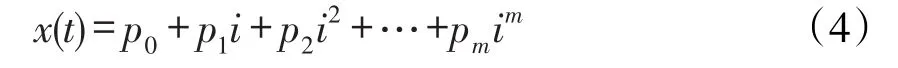
对于等间距采样,这里i=1,…,n。该模型具有2方面作用:一方面通过该函数对采样点进行回归,得到变量在各采样点的回归值,用回归值代替原测量值可以去噪;另一方面,该模型参数含有过程变量的变化信息,选取m=2,既能滤除噪声又能反映信号变化的基本趋势。相比较采用一次多项式滤波,2次多项式在能保证滤波效果的同时,降低了将一些非斜率变化的信号拟合到1次项中的可能性,减少了误判。
1.2 滑动窗口的自适应确定
在多项式滤波的过程中,只对当前窗口内的数据进行分析,窗口的长度可以根据历史稳态数据自适应地确定。在历史稳态数据库中,得到变量x的连续测量值序列。初始化滑动窗口的长度H=2,给定阈值α∈(0,1),取α=0.1。确定历史稳态工况数据的起始时间T1,将长度为H的滑动窗口的左端固定在T1处,分别计算多项式滤波前窗口内数据的标准差δ1和多项式滤波后窗口内数据的标准差δ2,并计算归一化标准差δH,见(5)式:

若δH>α,则令H=H+1,并再次计算当前窗口长度下的归一化标准差δH,直至δH≤α,此时的H即为所求的滑动窗口的长度。
1.3 稳态判断规则
对当前窗口中的数据进行多项式滤波后,得到反映该窗口内数据变化特征的曲线,见(6)式:

式中 p0、p1、p2分别为曲线方程零次项、1次项、2次项的系数,i=1,2,…,H,H为当前窗口的长度。p1系数能够反映当前窗口内的数据随时间变化的快慢,可以根据p1系数的大小来判断信号的稳态与否,其阈值根据“3δ”原则来确定。
令λ=3δ/H,其中δ为采集数据与滤波后数据之间偏差的标准差,若 ||p1<λ,则当前窗口内的数据处于稳态,否则处于非稳态。
1.4 具体步骤
(1)选取最能表征常减压装置的加工工况参数,读取历史稳态工况数据,自适应地确定滑动窗口的长度H。
(2)以当前时间Ta为基准,向前推4 h,确定数据采集的起始时间Tb:Tb=Ta-4,以3 min为时间间隔,采集该段时间范围内最能表征常减压装置的加工工况参数数据,分别组成数据段。
(3)将长度为H的滑动窗口左端固定在当前需要判断的数据段的起始位置,对当前窗口内的数据进行多项式滤波,依据稳态判断条件判断当前窗口内的数据是否处于稳态。若判断结果为非稳态,则此次判断结束。若判断结果为稳态,则继续步骤(4)。
(4)判断Tb至Ta时间范围内的用以稳态判断的参数数据是否已被全部检测,若尚未全部检测完成,则向右滑动窗口,滑动的距离见(7)式:
若全部检测完成,则输出平稳段的起始时间和结束时间,此次判断结束。
该方法用于常减压工况稳态检测的基本流程见图1。

图1 常减压稳态工况判断流程
2 实例分析
以某常减压装置为例,该装置具有炼油企业的典型工艺,包括初馏塔、常压塔和减压塔,选取原油加工流量、常压塔顶温度、实际换热终温、常二线抽出量、常一中回流量这5个最能表征常减压装置的加工工况参数。实际运行中,只有当选定的5个表征常减压装置加工工况参数都在稳态范围内,才进行优化计算。
文中仅对常二线抽出量、常一中回流量2个操作参数进行分析,其它参数的判断过程类似。
2.1 实际算例一
(1)选取常二线抽出量在2015年5月1日某段时间范围内的稳态工况数据,见表1。
选取常二线抽出量在2015年5月25日某段时间范围内的实时工况数据,见表2。
(2)依据(5)式,计算常二线抽出量在不同窗口长度下的归一化标准差,见表3。
依据表3中的归一化标准差 δH,需满足δH≤0.1,则常二线抽出量的窗口长度选定为H=37。
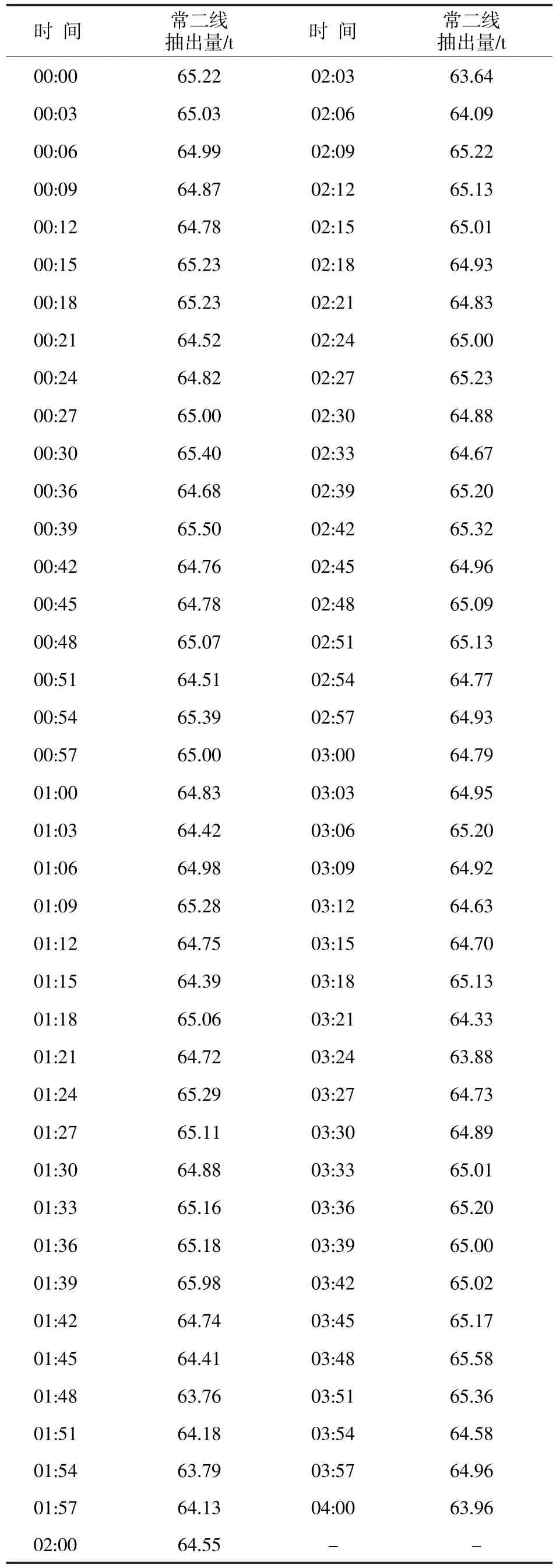
表1 常二线抽出量历史稳态工况数据

表2 常二线抽出量实时工况数据

表3 常二线抽出量的归一化标准差
(3)将长度为H的滑动窗口左端固定在数据段起始点,对当前窗口内的数据进行多项式滤波,并计算当前窗口内测量数据与拟合数据之间偏差的标准差。若满足稳态判断条件,且当前时段内的参数尚未全部检测完成,则依据式(7)向右移动滑动窗口继续判断。计算结果见表4。
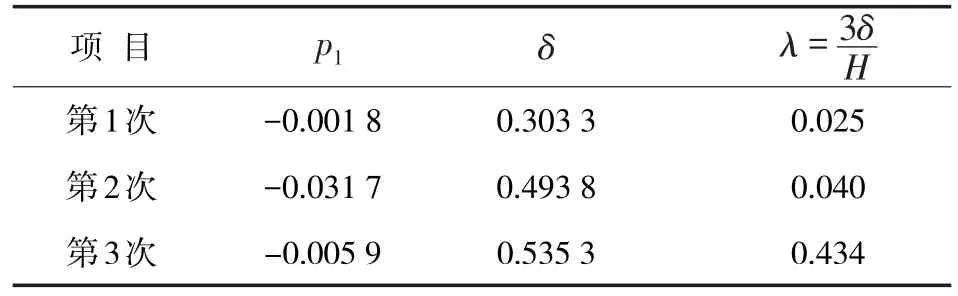
表4 常二线抽出量滤波后1次项系数及误差标准差
依据表4,在每个窗口内均满足稳态判断条件,该段时间范围内(2015-05-25.05:00至2015-05-25.09:00)常二线抽出量处于稳态。
2.2 实际算例二
(1)选取常一中回流量在2015年5月1日某段时间范围内的稳态工况数据。采用前述方法,计算常一中回流量在不同窗口长度下的归一化标准差,见表5。
根据计算结果,需满足δH≤0.1,则常一中回流量的窗口长度选定为25。
(2)选取常一中回流量在2015年5月25日某段时间范围内的实时工况数据。
(3)采用前述方法,计算常一中回流量在相应窗口下1次项系数和测量误差的标准差,结果见表6。
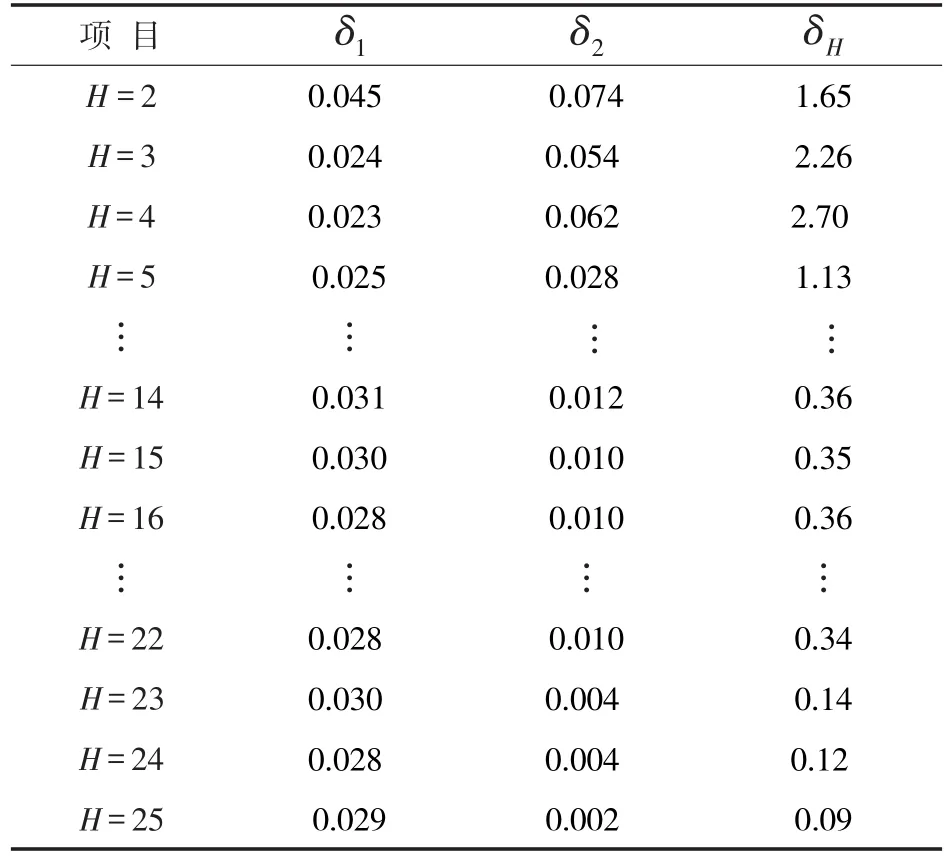
表5 常一中回流量的归一化标准差

表6 常一中回流量滤波后1次项系数及误差标准差
依据表6,在第4次进行多项式滤波后存在|p1|≥λ,依据稳态判断条件,该段时间范围内(2015-05-25.05∶00至2015-05-25.09∶00)常一中回流量不处于稳态,此次判断结束。
3 应用效果
在金陵石化公司常减压优化项目中,采用Petro-Sim软件对常减压进行优化模拟计算。优化的前提是装置处于稳态工况。收集该装置2014年9月28日至2014年11月27日这段时间范围内每天上午08∶00的常二线收率变化情况,见图2。

图2 金陵石化公司常减压装置常二线收率
在9月28日至10月28日该段时间范围内,采用早期常减压工况稳态判别的方法对装置进行稳态判别,对判断为稳态的工况进行实时优化。经过优化后的常二线收率在此时间段内虽略有波动,但整体上并无明显变化。此后,采用该文提出的稳态检测方法对常减压装置进行稳态判别,在后续装置的实时优化中发现,常二线收率有了明显的提高,与此前相比提高约3%。应用该方法对常减压装置进行稳态检测,减少了误判,更加有利于常减压装置后续的实时优化。
4 结束语
基于多项式滤波的常减压工况稳态判别方法,通过选择5个最能表征常减压装置的加工工况参数组成数据段,采用滑动窗口对当前窗口内的数据进行多项式滤波,根据滤波后多项式1次项系数的大小,综合判断常减压装置是否处于稳态。实际应用中,很好地减少了测量误差和有效地利用了测量数据,从而能够在后续装置的实时优化中提高产品的收率,对生产效率和经济效益的提高具有重要作用,该方法对于解决炼油工艺中的数据稳态判别问题具有一定的参考价值。
[1]李志强.原油蒸馏工艺与工程[M].北京:中国石化出版社,2010:33-43.
[2]刘吉臻,高萌,吕游,等.过程运行数据的稳态检测方法综述[J].仪器仪表学报,2013,34(8):1739-1748.
[3]Narasimhan S,Shan Kao Chen,Mah R.S.H.Detecting changes of steady state using the mathematical theory of the evidence[J]. A ICHE J,1987,33(1):1430-1432.
[4]金思毅,周传光.化工过程稳态检验的区间拓展法[J].高校化学工程学报,2000,14(1):71-76.
[5]李博,陈丙珍,胡慧琴,等.稳态过程在线数据校正技术的工业实施[J].石油化工,2000,29(10):768-771.
[6]贾秋玲,袁冬莉,栾云风.基于ATLAB7.X/Simulink/Stateflow系统仿真分析与设计[M].西安:西北工业大学出版社,2006:8-27.
[7]付克昌,戴连奎,吴铁军.基于多项式滤波算法的自适应稳态检测[J].化工自动化及仪表,2006,33(5):18-21.
Steady-state discrimination of working condition of atmospheric&yacuum distillation unit based on polynomial filtering
Luo Fan1,2,Chen Xisong2,Zhang Xiangrong1,Mei Bin1
(1.Nanjing Richisland Information Engineering Co,Ltd.Nanjing 210061,China;2.School of Automation,Southeast University,Nanjing 210096,China)
Steady-state working condition detection for atmospheric&vacuum distillation unit plays an important role in the realtime optimization.Some methods of steady-state detection have been presented such as fixed window,partition statistics,etc. However,these methods are sensitive to various influences which may lead to false detection.In this paper,a new method of steadystate detection based on polynomial filtering is proposed.Polynomial filtering is used to fit the data in the current window and the first order coefficient of the curve equation is used to decide whether the state of the unit is steady or not.The length of the sliding window can be adaptively determined according to the historical steady-state data.The effectiveness of the method has been proved through practical cases.
atmospheric&vacuum distillation unit;steady-state detection;polynomial filtering;sliding window;self-adaption
TE624.2
B
1671-4962(2017)01-0051-05
2016-11-18
罗凡,男,现就读于东南大学自动化学院,攻读硕士学位,研究方向为控制理论与控制工程。

