Tikhonov正则化在运行工况传递路径分析的应用*

成 玮， 卢英英， 陆建涛， 张周锁

(1.西安交通大学机械制造系统工程国家重点实验室 西安，710049)(2.西安交通大学机械工程学院 西安，710049)

Tikhonov正则化在运行工况传递路径分析的应用*

成 玮1,2， 卢英英2， 陆建涛2， 张周锁1,2

(1.西安交通大学机械制造系统工程国家重点实验室 西安，710049)(2.西安交通大学机械工程学院 西安，710049)

针对传统运行工况传递路径分析(operational transfer path analysis，简称OTPA)存在的不足，通过理论和试验分析，提出基于Tikhonov正则化方法的OTPA反问题模型。首先，分析Tikhonov正则化方法的理论优势，给出Tikhonov正则化参数选择的依据，同时调节电机转速获得不同运行工况数据，利用奇异值分解方法研究壳体结构的振动传递路径，分析传统OTPA算法总贡献量误差及路径贡献量估计精度；其次，分析运行工况数据是否满足Picard条件，提出基于Tikhonov正则化方法的OTPA算法，并分析Tikhonov正则化参数对所提出算法的影响。分析结果表明，所提出的方法显著减小了总贡献量和路径贡献量误差以及路径误判现象。该研究可为振动噪声监控与减振降噪提供理论依据。

运行工况传递路径分析； Tikhonov正则化； 奇异值分解； Picard条件； 减振降噪

引 言

水下航行器的声隐身性能是衡量其安全性和作战能力的重要指标[1]，在低、中速航行时，动力机械设备振动是产生辐射噪声的主要来源[2]。轿车和高速列车的振动噪声是评价车辆性能的重要指标[3]。因此，机械设备振动噪声的有效监测与控制对于提高装备性能具有重要工程意义。

运行工况传递路径分析是一种用于识别和定量分析机械系统振动噪声传播路径的方法[4]。由于建模快速高效，OTPA广泛应用于实际工程[5]。Roozen等[6]基于奇异值分解，建立了齿轮箱的OTPA模型并研究了振动传递路径。Putner等[7]利用OTPA成功估计了不同声源对车外噪声的贡献量。Yan等[8]基于局部奇异值分解，研究了板辐射噪声对车内噪声的影响。传统OTPA采用奇异值分解[9]，获取求解传递率函数的主成分，并建立传递路径模型[10]。由于系统模态会产生路径交叉耦合使系统病态，外加测试噪声影响，传统OTPA不可避免出现贡献量过估计现象和误判现象[11]。Tikhonov正则化方法[12]充分考虑了不适定问题[13]求解的不稳定性和噪声污染等因素，广泛应用于反问题求解[14-15]。OTPA模型属于反问题，即通过运行工况数据识别系统的传递率函数矩阵。当前，利用Tikhonov正则化的OTPA方法研究很少。

笔者提出了基于Tikhonov正则化的OTPA反问题模型。首先，给出了传统OTPA和基于Tikhonov正则化OTPA的基本理论；其次，分析了加筋圆柱壳试验台(用于模拟水下航行器的动态特性)运行工况数据的相关性，建立了试验台的传统OTPA模型并研究路径贡献量，分析了奇异值和矩阵条件数对贡献量准确度的影响；最后，检验了Picard条件，分析了正则化参数对基于Tikhonov正则化OTPA模型精度的影响。通过与传统OTPA模型比较，验证了基于Tikhonov正则化OTPA模型在路径贡献量识别中具有更高的精度。

1 OTPA基本理论

1.1 传统OTPA

OTPA[4]线性系统为

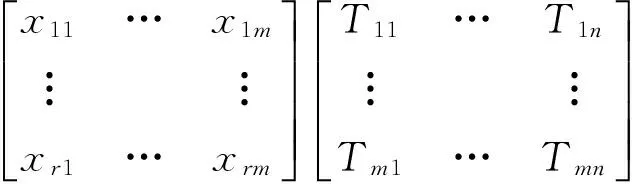
(1)

其中：T为未知传递率函数矩阵；X为已知激励源参考点试验工况矩阵；Y为已知目标点试验工况矩阵；m为参考点个数；n为目标点个数；r为试验工况个数。

由于OTPA通过试验工况响应信号估计传递率函数矩阵，因此对于式(1)：a.为了保证参考点试验工况矩阵的可逆性，试验工况个数必须等于或大于参考点个数，即r≥m;b.结构模态引起的激励在其他路径上产生响应(路径耦合)，容易出现路径误判。

1.2 传统OTPA算法

传统OTPA方法通过求解最小二乘问题估计传递率函数矩阵，即

(2)

具体算法如下：

1) 对X奇异值分解

(3)

2) 确定X截断奇异值

(4)

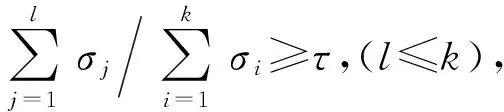
3) 估计传递率函数矩阵

(5)

4) 分析传递路径

Y′=X′T

(6)

其中：X′为参考点实际工况数据；Y′为传统OTPA识别的目标点振动响应。

1.3 基于Tikhonov正则化的OTPA

针对传统OTPA不足，式(2)仅考虑解的拟合程度。式(3)贡献量为工程经验值(τ≥85%)。Tikhonov正则化广泛应用于反问题研究[14-15]，对于线性系统

Ax=b

(7)

其中：Am×n(m≥n)为已知系数矩阵；bm×1为已知系数向量；xn×1为未知向量。

在实际工程中，噪声干扰会导致式(7)的解失去物理意义。Tikhonov正则化通过修改系数矩阵或约束未知向量获得最优解。

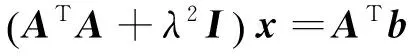
(8)

其中：‖‖为Euclidean范数；λ>0为正则化参数。

对比式(2)和式(8)，式(8)同时考虑解的拟合程度和稳定性，因此基于Tikhonov正则化的OTPA方法具有理论优势。

式(8)的解可表达为

(9)

结合式(3)可得

(10a)

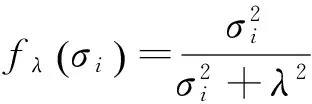
(10b)

离散傅里叶系数和奇异值是Picard条件的主要构成要素，且离散傅里叶系数比奇异值趋于零的速度快。若式(7)满足离散Picard条件[16]，则能够求其具有物理意义的正则逼近解。式(8)的关键是选择正则化参数λ，即通过λ平衡解的拟合程度和稳定性，Tikhonov正则化参数的选择方法主要有广义交叉验证(generalized cross validation，简称GCV)方法[17]和L曲线方法[18]。

GCV通过求解式(11)极小值确定参数λ，即

(11)

(12)

根据式(11)和式(12)，GCV方法和L曲线方法的基本思想都是确定的参数λ使残量Axλ-b和解xλ的范数同时保持在较小的水平上，即平衡解xλ的拟合程度和稳定性。

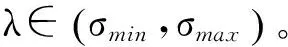
1.4 基于Tikhonov正则化的OTPA算法

算法如下：

1) 融合式(7)和式(1)，建立OTPA模型；

2) 融合式(3)和式(9)，推导出式(10)；

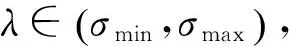
4) 分析传递路径

Y′=X′Tλ

(13)

其中：X′为参考点实际工况数据；Y′为基于Tikhonov正则化OTPA识别的目标点振动响应。

2 传统OTPA试验研究

2.1 试验台及试验工况简介

根据某型号舰艇壳体结构，搭建了圆柱加筋壳体试验台，主要由薄壁圆柱壳体结构及7个均匀分布加强筋组成。远离加强筋一端布置有大小两台偏心振动电机模拟振源，通过壳体结构不同位置传感器获取结构振动加速度响应信号。试验台主要设备实物图与测点布置图分别如图1和图2所示。

图1 试验台及主要设备实物图Fig.1 The physical diagram of test bed and major equipments

圆圈内数字为传感器编号；传感器1，2，3分别为小电机的竖直方向、水平方向和基座附近；传感器4，5，6分别为大电机的竖直方向、水平方向和基座附近图2 传感器空间位置示意图(单位：mm)Fig.2 Positions of the sensors (unit: mm)

大、小电机参考点分别为传感器4与传感器1，目标点为传感器13，电机不同转速下的运行工况数据如表1所示。

当试验运行工况数据相关性较大时，式(5)中小奇异值较多，导致传递率函数矩阵估计不准确，影响OTPA模型的精度。传感器1和4不同运行工况数据的相关系数如图3所示。不同工况下传感器1，4和13的相关系数如图4所示。

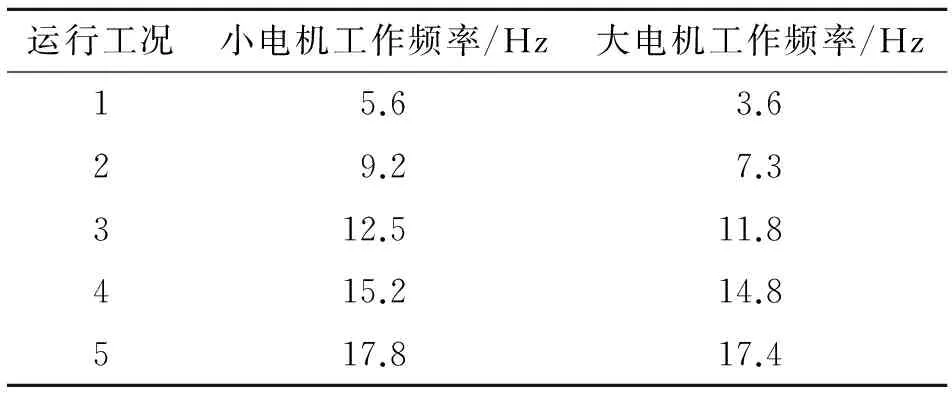
表1 不同电机转速的运行工况

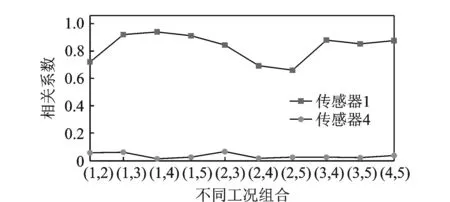
图3 不同工况数据相关性Fig.3 The correlation of data in different operating conditions

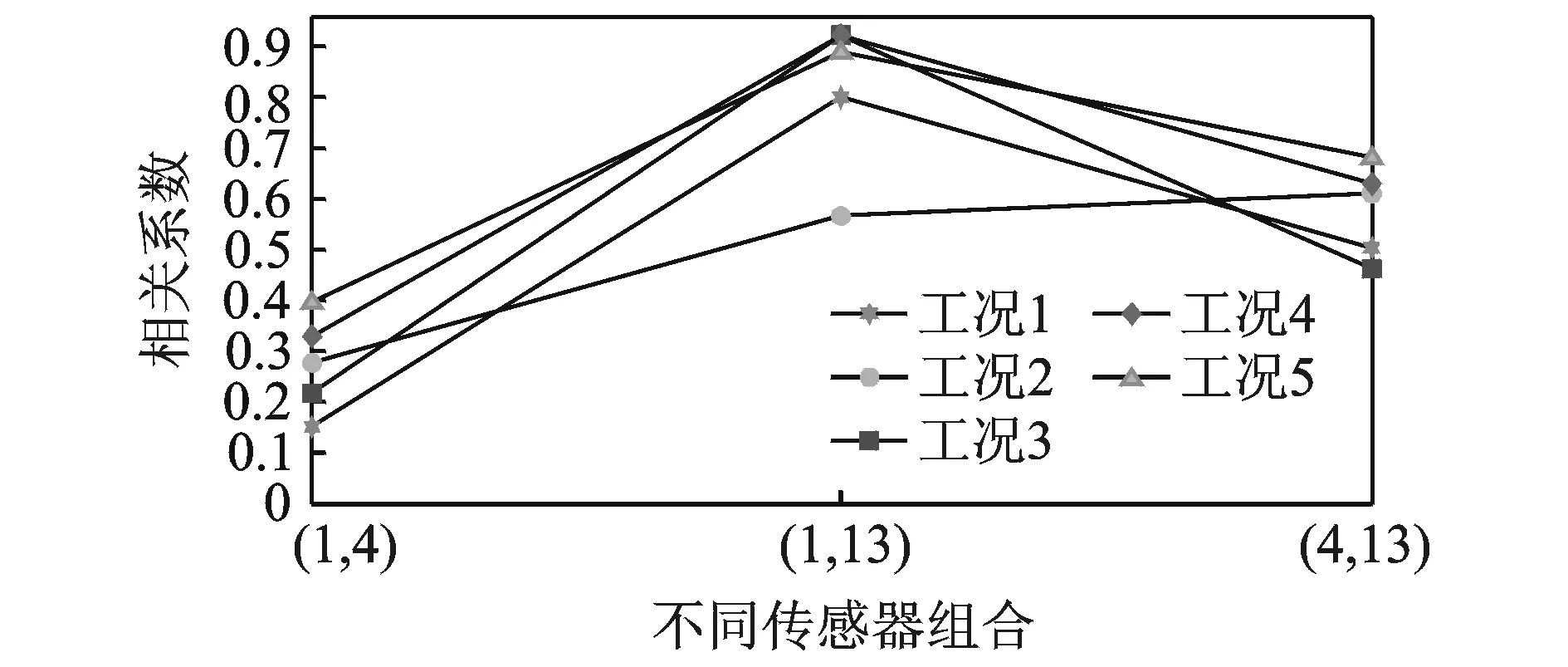
图4 不同传感器数据相关性Fig.4 The correlation of data between different sensors

由图3可得，传感器4不同工况的相关系数小于0.1，表明参考点4不同工况的相关性很弱，可保证参考点试验运行工况矩阵求逆良态。

由图4可得，不同工况下传感器1和4的相关系数约为0.15～0.4，表明大小电机耦合较弱，参考点1和4分别表示小电机与大电机的振源特性。不同工况下传感器1和13的相关系数大部分高于0.80，传感器4和13的相关系数约为0.5～0.7，表明传感器13的振动来源于小电机和大电机，且与小电机相关性更高。

综上分析，参考点4不同工况的相关性很弱，可保证矩阵良态；参考点1和4的相关系数较小，表明振源耦合较弱。综合分析可得参考点和运行工况的选择较为合理，可用于研究运行工况振动路径传递。

2.2 传统OTPA

OTPA基本思路：利用已知运行工况数据识别传递率函数矩阵，分析任意运行工况下振动噪声传递路径。利用表1的运行工况数据，根据式(1)可得试验台OTPA模型为

(14)

用传统OTPA算法计算的式(14)参考点矩阵奇异值和条件数分别如图5和图6所示。

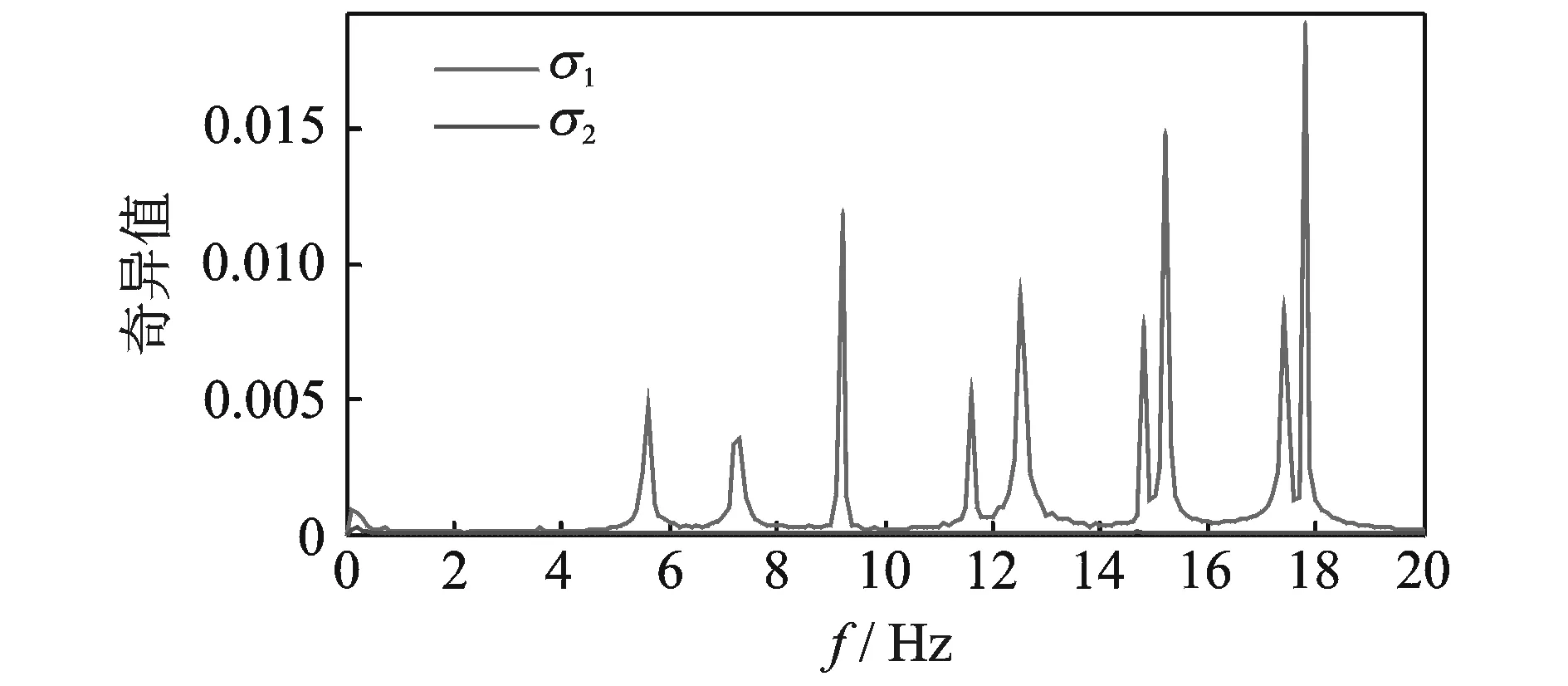
图5 试验台OTPA矩阵奇异值Fig.5 Matrix singular values of test bench OTPA

图5表明试验台OTPA模型有两个奇异值，最大奇异值和最小奇异值分别为0.02和3.64×10-19，前者代表小电机振动，后者代表大电机振动，即小电机振动强度较大，与图4结论吻合。

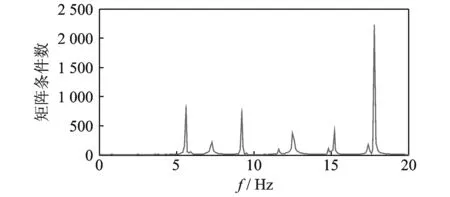
图6 试验台OTPA矩阵条件数Fig.6 Matrix condition number of test bench OTPA

图6表明试验台OTPA模型矩阵条件数很大，导致不同频率下试验台OTPA模型不稳定。导致试验台OTPA模型不稳定因素有：测试噪声和图3所示参考点1不同工况相关性(相关系数约为0.7～0.9，即相关性很大)。

传统OTPA计算传递率函数如图7所示。T11为参考点1与传感器13的传递率函数，T12为参考点4与传感器13的传递率函数。

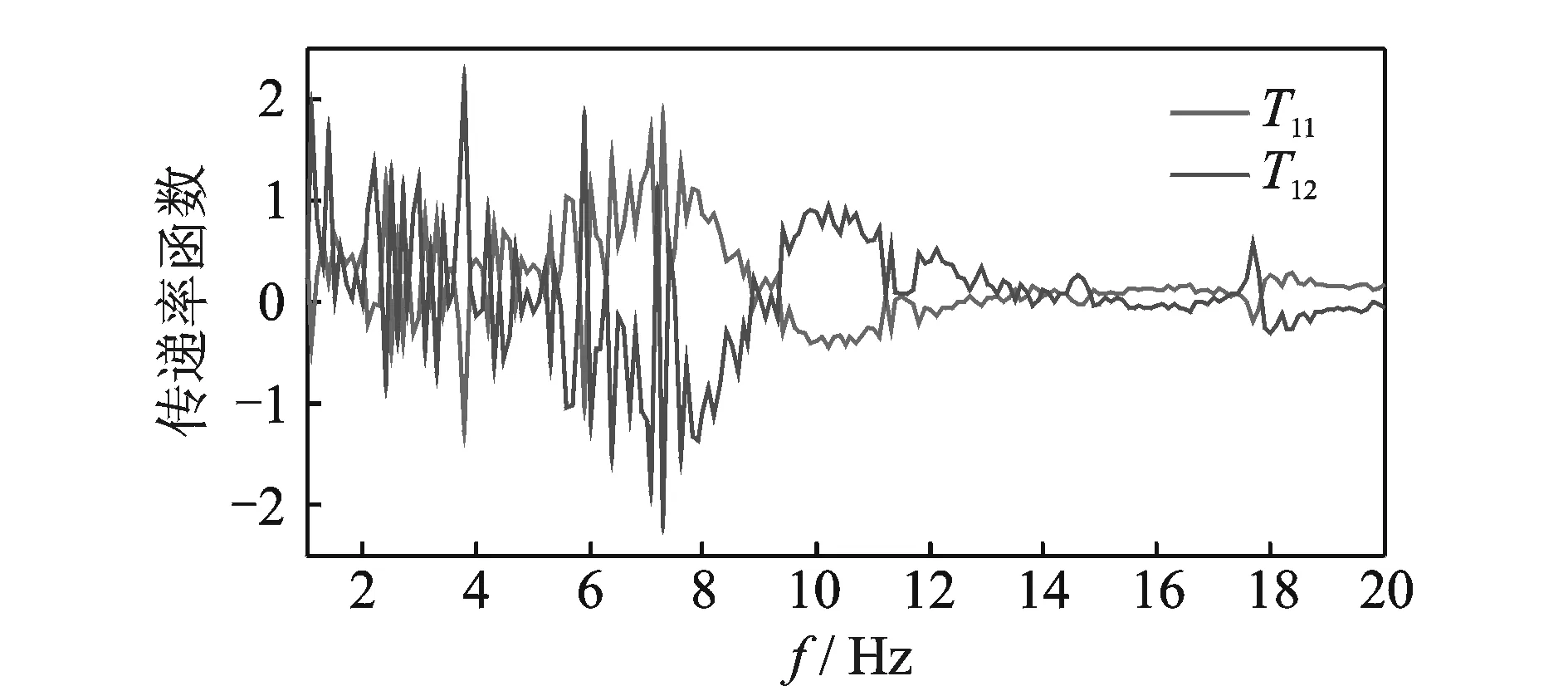
图7 传统OTPA传递率函数Fig.7 Traditional OTPA transmissibility functions of the test bed

传统OTPA算法识别的大小电机与目标点传递率函数波动较大，小电机对应的传递率函数相比波动稍小。分析认为，参考点不同工况的相关性和测试噪声导致矩阵条件数很大，使试验台OTPA模型不稳定，最终导致传递率函数波动较大；小电机对应的奇异值较大，受噪声干扰较小，因此小电机对应的传递率函数较稳定。因此，图7与图3～6的结论一致。

假设实际工况为大小电机分别以工作频率11.8 Hz和15.2 Hz运行。传统OTPA算法计算式(14)传感器13的总贡献量、大电机路径贡献量和小电机路径贡献量分别如图8～10所示。

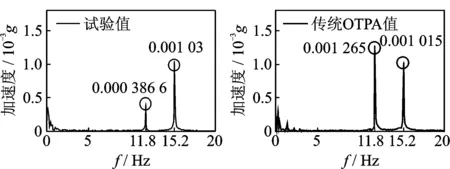
图8 总贡献量(传统OTPA)Fig.8 The total contributions (traditional OTPA)

由图8可知，15.2 Hz时传统OTPA算法总贡献量与试验值一致，而11.8 Hz时相差较大。

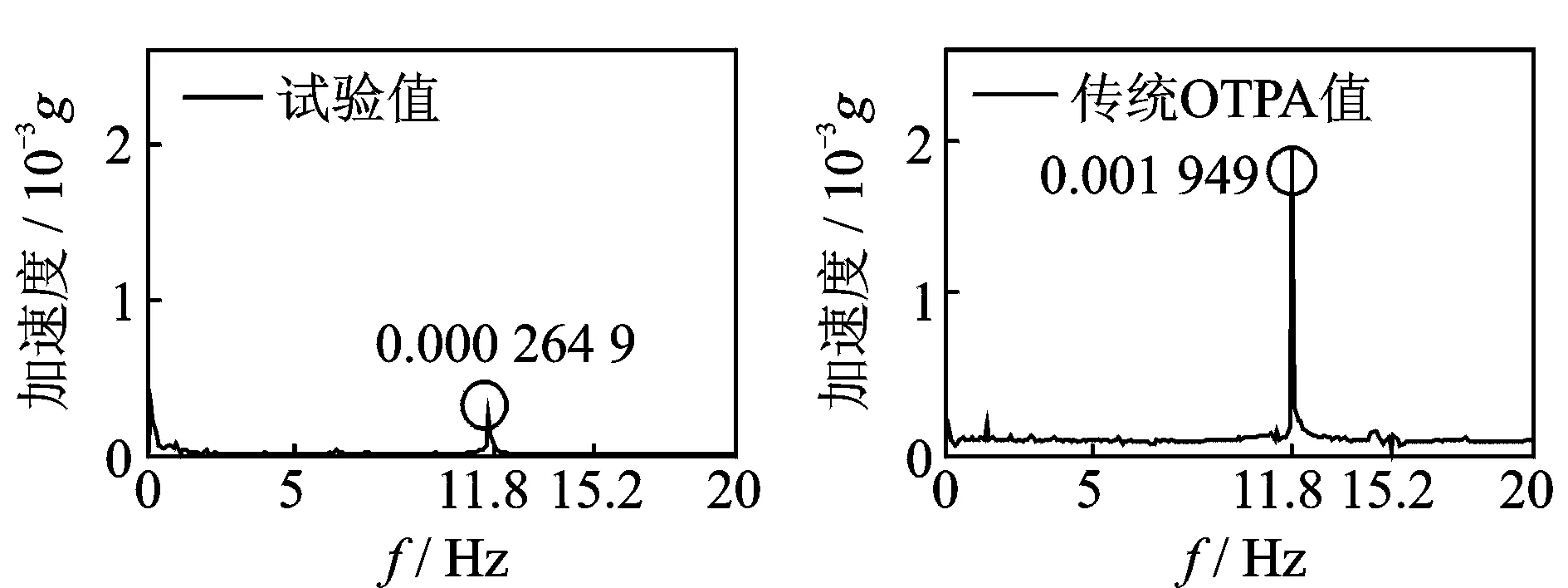
图9 大电机路径贡献量(传统OTPA)Fig.9 The big motor path contribution (traditional OTPA)

由图9可得，大电机贡献量试验值约为0.000 3g，而传统OTPA值约为0.002g，即传统OTPA算法大电机路径贡献量误差很大。

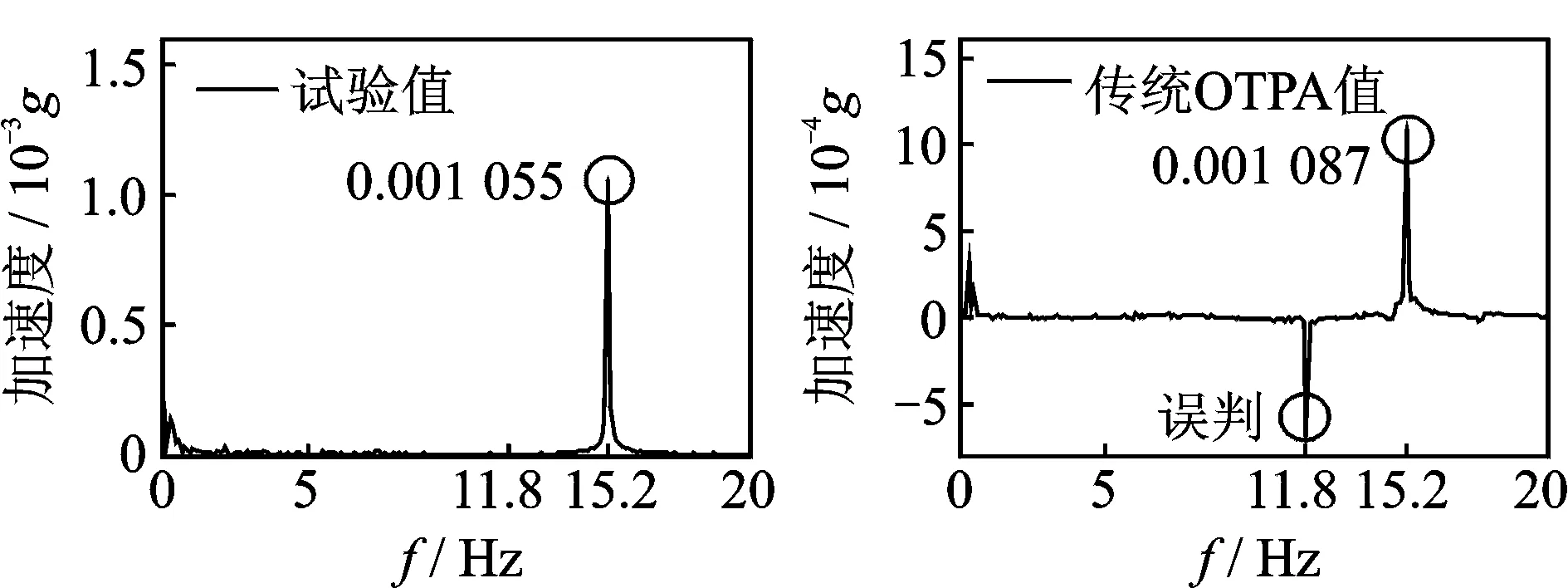
图10 小电机路径贡献量(传统OTPA)Fig.10 The small motor path contribution (traditional OTPA)

小电机工作频率为15.2 Hz，由图10可得，11.8 Hz时传统OTPA算法小电机路径贡献量较大，出现严重误判。由于小电机工作频率为15.2 Hz，且小电机对应传递率函数较稳定，所以15.2 Hz时传感器13总贡献量和小电机路径贡献量均与试验值吻合较好。

通过以上分析，传统OTPA可定性识别振动传递路径，即传感器13振动能量源于工作频率分别为11.8 Hz和15.2 Hz振源。稳定性较差的大电机传递率函数导致11.8 Hz时出现大电机路径贡献量误差很大(图9)和小电机路径贡献量误判(图10)。

传递率函数识别方法是OTPA模型的关键技术，但是容易受到参考点不同工况相关性和测试噪声影响。大小电机分别以工作频率11.8 Hz和15.2 Hz运行时，参考点和目标点信号相关系数如表2所示。传感器1和4、1和13、4和13的相关系数分别为0.328，0.908和0.571，表明参考点1和4的相关性较弱，大小电机耦合较小，可分别表示振源特性；传感器13振动主要源于小电机；分析结论与图3和图4结论一致。

表2 参考点和目标点的相关系数

Tab.2 Coefficients between reference points and target points

相关系数传感器1传感器4传感器13传感器110.3280.908传感器40.32810.571传感器130.9080.5711

综上分析，噪声干扰和参考点不同工况的相关性导致传统OTPA算法精度较低，在与目标点相关性较弱振源对应频率下，总贡献量识别误差较大，路径贡献量失真较严重。

3 Tikhonov正则化OTPA模型试验研究

3.1 Picard条件检验

Picard条件是检验试验台OTPA模型是否具有物理意义Tikhonov正则化解的重要条件，试验台OTPA模型Picard条件如图11所示。奇异值1和2曲线分别位于对应离散傅里叶系数曲线的上方，表明试验台OTPA模型满足Picard条件，即可通过Tikhonov正则化方法求解其有物理意义的正则解。

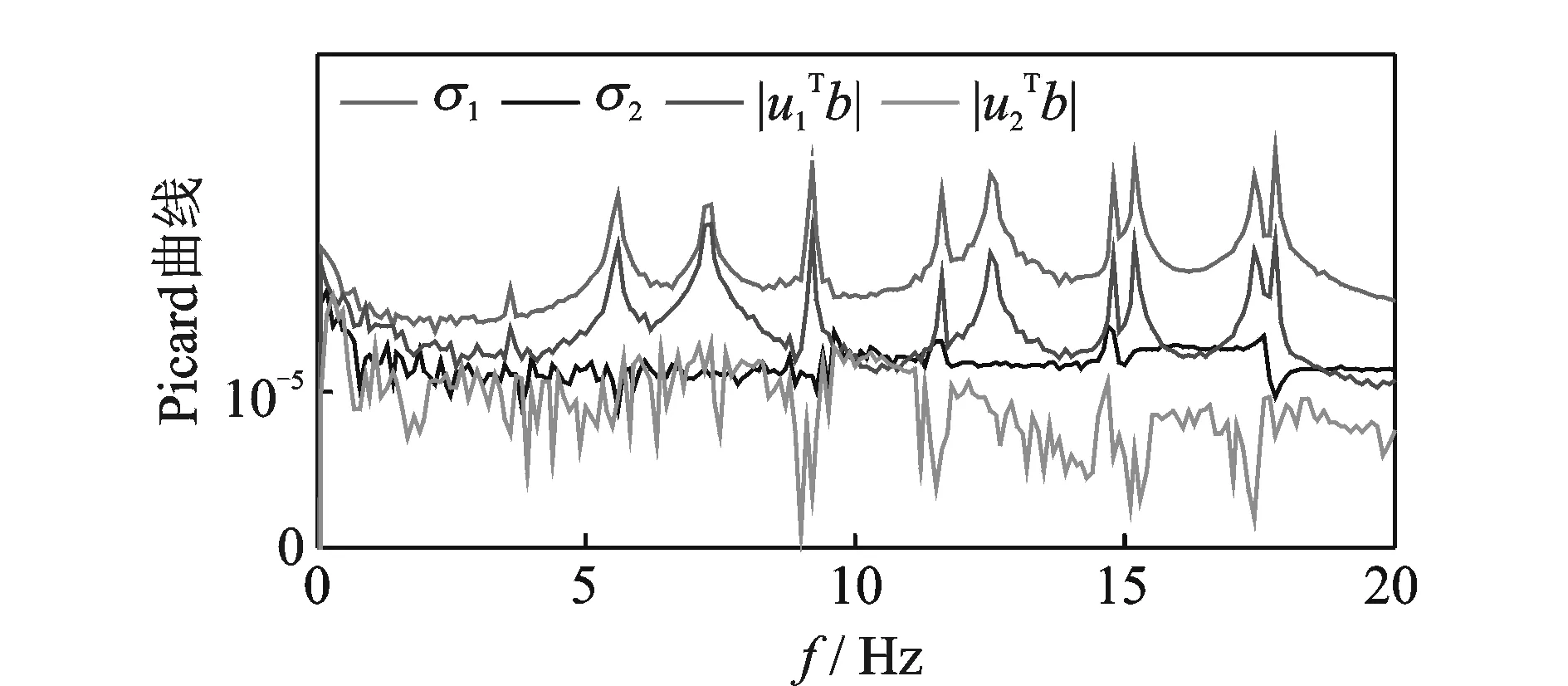
图11 试验台OTPA模型的Picard条件Fig.11 Picard conditions of OTPA model for the test bed

3.2 基于Tikhonov正则化的OTPA

通过式(10)中不同Tikhonov正则化参数λ识别试验台OTPA传递率函数如图12和图13所示。图12和图13表明传递率函数受正则化参数λ的影响较大。同时λ越小，传递率函数越接近传统OTPA算法识别的传递率函数；λ越大，传递率函数出现明显峰值，且过滤掉表1大小电机工作频率以外其他频段的干扰噪声。

图12 λ对小电机相应传递率函数的影响Fig.12 λ effects on transmissibility functions of small motor

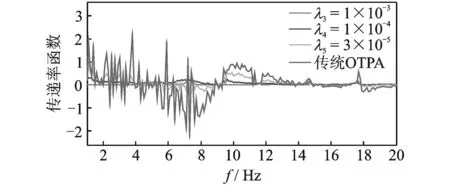
图13 λ对大电机传递率函数的影响Fig.13 λ effects on transmissibility functions of big motor

基于Tikhonov正则化OTPA算法的分析结果如图14～16所示。

图14 λ对总贡献量的影响Fig.14 λ effects on total contributions

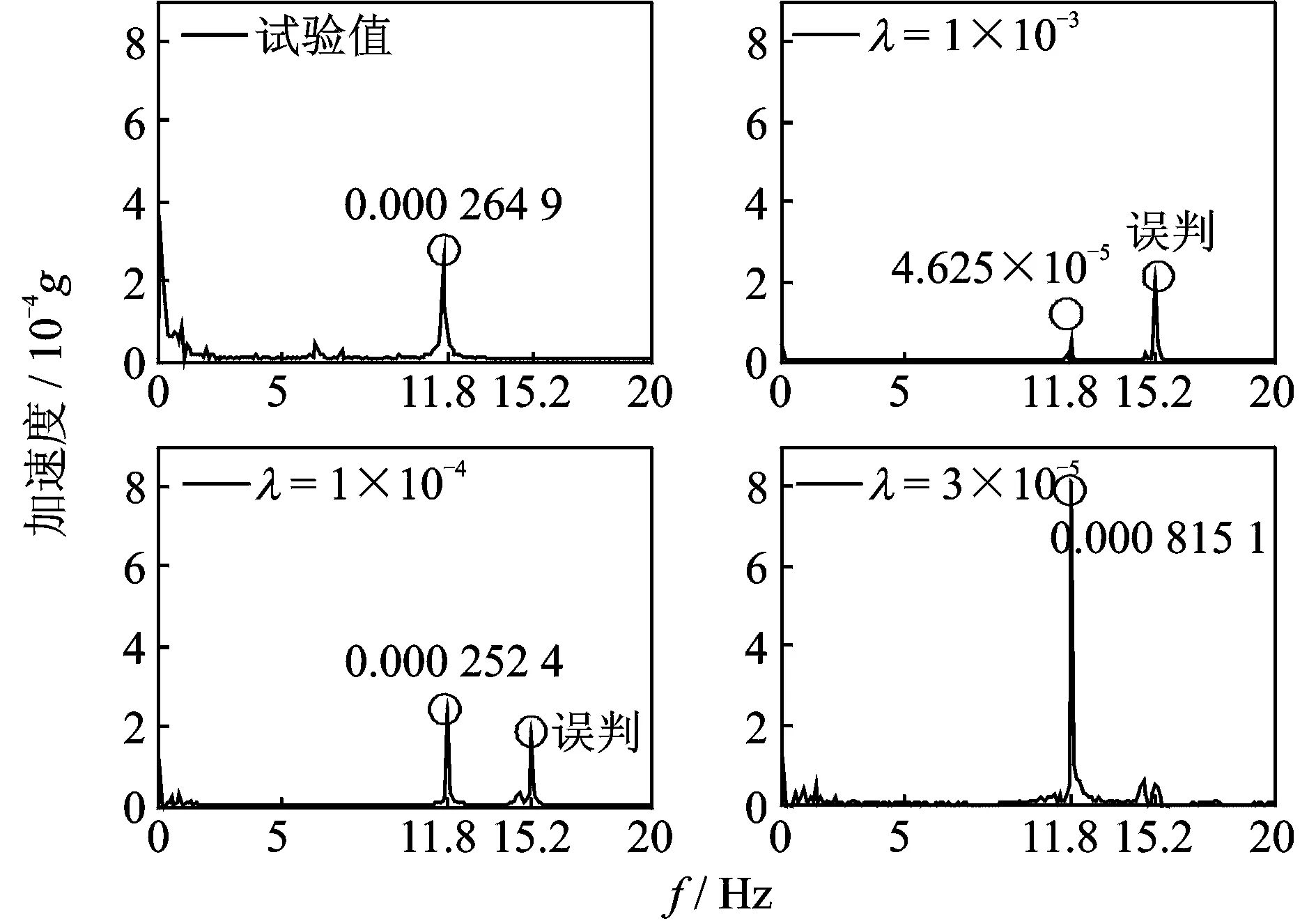
图15 λ对大电机路径贡献量的影响Fig.15 λ effects on path contributions of big motor

图14为不同λ条件下总贡献量曲线。显然，λ对总贡献量影响很大。图15为不同λ条件下大电机路径贡献量曲线。当λ=1×10-3和λ=1×10-4时，大电机路径贡献量出现误判，但当λ=3×10-5时，路径误判消除。

图16 λ对小电机路径贡献量的影响Fig.16 λ effects on path contributions of small motor

图16为不同λ条件下小电机路径贡献量曲线，当λ=1×10-3和λ=1×10-4时，小电机路径贡献量出现误判，但当λ=3×10-5时，路径误判消失。

综上分析，应用Tikhonov正则化方法建立OTPA模型具有实用性和有效性；Tikhonov正则化参数λ严重影响总贡献量和路径贡献量的分析结果；通过调节Tikhonov正则化参数λ可消除路径误判。

结合图8～10，图14～16，传统OTPA算法和基于Tikhonov正则化方法OTPA算法分析结果的相对误差对比如表3所示。

表3 传统OTPA与Tikhonov正则化误差

Tab.3 Errors of traditional OTPA and Tikhonov regularization

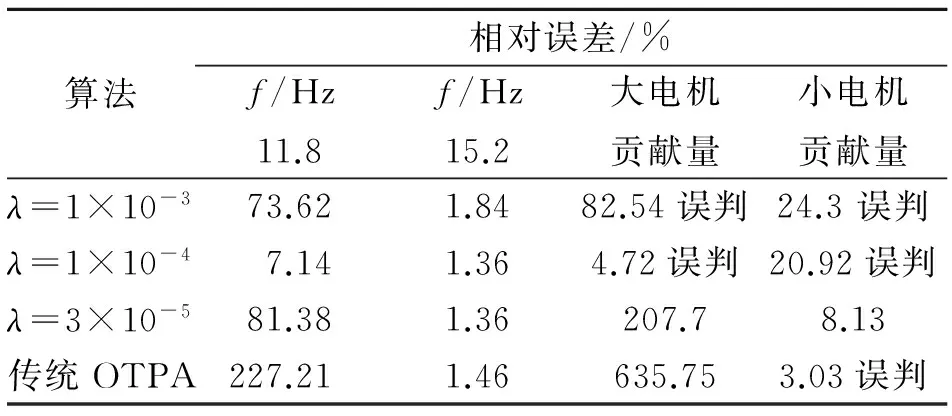
算法相对误差/%f/Hz11.8f/Hz15.2大电机贡献量小电机贡献量λ=1×10-373.621.8482.54误判24.3误判λ=1×10-47.141.364.72误判20.92误判λ=3×10-581.381.36207.78.13传统OTPA227.211.46635.753.03误判

表3中，当λ=1×10-4时，与传统OTPA算法分析结果比较，Tikhonov正则化方法将总贡献量相对误差分别从227.3%和1.46%减小到7.14%和1.36%。因此，Tikhonov正则化方法显著提高了试验台OTPA模型总贡献量识别精度(其中λ=1×10-4最优)。当λ=3×10-5时，与传统OTPA算法分析结果相比，Tikhonov正则化方法将大电机路径贡献量相对误差从635.75%减小到207.7%，同时消除小电机路径贡献量严重误判现象，且小电机路径贡献量相对误差为8.13% 。因此，Tikhonov正则化方法很好地克服了传统OTPA路径贡献量误差过大缺点，与此同时很好地弥补了传统OTPA路径贡献量误判缺陷。

综上分析，Tikhonov正则化方法同时考虑了试验台OTPA模型传递率函数矩阵的拟合程度和稳定性，显著提高了OTPA总贡献量和路径贡献量识别准确度，且抑制了OTPA路径贡献量误判缺陷。

4 结 论

1) 传统OTPA算法仅考虑拟合程度，工程经验值不足和测试噪声等因素易导致路径贡献量和总贡献量计算误差较大，难以定量识别振动传递路径。

2) 基于Tikhonov正则化方法OTPA同时考虑拟合程度和稳定性，显著提高了路径贡献量和总贡献量计算精度，同时有效克服了传统OTPA路径贡献量误判的不足。

3) 理论与试验分析表明，基于Tikhonov正则化OTPA优于传统OTPA，可实现振动传递路径定量识别，为结构优化设计和减振降噪提供理论依据。

[1] 张磊, 曹跃云, 杨自春，等. 运行工况下舰船振动-声传递路径分析及试验[J]. 华中科技大学学报:自然科学版, 2013, 41(2): 42-47.

Zhang Lei, Cao Yueyun, Yang Zichun, et al. Theoretical analysis and experimental validation of vibration-acoustic transferring paths of ships under operational conditions[J]. Journal of Huazhong University of Science & Technology: Natural Science Edition, 2013, 41(2):42-47. (in Chinese)

[2] 成玮, 张周锁, 何正嘉，等. 基于独立分量分析的潜艇振源贡献量定量计算方法[J]. 机械工程学报, 2010, 46(7): 83-87.

Cheng Wei, Zhang Zhousuo, He Zhengjia, et al. Quantitative calculation of vibration source contributions of submarines based on independent component analysis[J]. Journal of Mechanical Engineering, 2010, 46(7):83-87. (in Chinese)

[3] Li W, Wang D F, Chen S M, et al. Transfer path analysis of power train vibration on driver's noise[C]∥7th International Conference on Natural Computation (ICNC). Shanghai: IEEE, 2011: 2353-2357.

[4] Yoshida J, Noumura K. Method of transfer path analysis for interior vehicle sound using principal component regression method[J]. Honda R&D Technical Review, 2006,18(1):136-141.

[5] Janssens K, Mas P, Gajdatsy P, et al. A novel path contribution analysis method for test-based NVH trouble shooting[C]∥Proceedings of Acoustics 2008. Geelong, Victoria, Australia:[s.n.],2008: 3673-3683.

[6] Roozen N B, Leclere Q, Sandier C. Operational transfer path analysis applied to a small gearbox test set-up[C]∥Proceedings of Acoustics 2012. Nantes, France: [s.n.], 2012:3467-3473.

[7] Putner J，Lohrmann M，Fastl H. Contribution analysis of vehicle exterior noise with operational transfer path analysis[C]∥Proceedings of Meetings on Acoustics. Montreal, Canada:[s.n.], 2013,19,040035(1-9).

[8] Yan Li, Jiang Weikang. Research on the procedure for analyzing the sound quality contribution of sound sources and its application[J]. Applied Acoustics, 2014, 79:75-80.

[9] 胥永刚，谢志聪，孟志鹏，等. 基于奇异值分解的磁记忆信号特征提取方法[J]. 振动、测试与诊断,2014,34(6)：1106-1109.

Xu Yonggang, Xie Zhicong, Meng Zhipeng, et al. The signal feature extraction method of magnetic memory based on singular value decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(6):1106-1109. (in Chinese)

[10]Klerk D, Ossipov A. Operational transfer path analysis: theory, guidelines and tire noise application[J]. Mechanical Systems and Signal Processing, 2010, 24(7): 1950-1962.

[11]Peter G, Karl J, Ludo G. Critical assessment of operational path analysis: mathematical problems of transmissibility estimation[J]. The Journal of the Acoustical Society of America, 2008, 123(5): 9359-9364.

[12]Hadamard J. Sur les problems aux derivees partielles et leur signification physique[R]. Bulletin: Princeton University, 1902.

[13]Tikhonov A N, Arsenin V Y. Solution of ill-posed problems [J]. Mathematics of Computation, 1978,32(14):491.

[14]Tikhonov A. Solution of incorrectly formulated problems and the regularization method[J]. Doklady Akademii Nauk SSSR, 1963,151(3):501-504.

[15]马超，华宏星 . 正则化技术在状态空间载荷识别中的应用[J]. 振动、测试与诊断, 2014, 34(6): 1154-1158.

Ma Chao, Hua Hongxing. The application of regularization technique for load identification in state space[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(6): 1154-1158. (in Chinese)

[16]Hansen P C. The discrete picard condition for ill-posed problems[J]. BIT Numerical Mathematics, 1990,30(4):658-672.

[17]Golub G H, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter [J]. Technometrics, 1979, 21(2): 215-223.

[18]Hansen P C. Analysis of discrete ill-posed problems by means of the l-curve[J]. SIAM Review, 1992, 1(34): 561-580.

10.16450/j.cnki.issn.1004-6801.2017.01.009

国家自然科学基金资助项目(51305329)；中国博士后科学基金资助项目(2014T70911，2013M532032)；高等学校博士学科点专项科研基金资助项目(20130201120040)；陕西省博士后基金资助项目

2015-02-09；

2015-04-20

TH128； TB535

成玮，男，1983年6月生，副教授。主要研究方向为机械系统状态监测与故障诊断。曾发表《A comprehensive study of vibration signals for a thin shell structure using enhanced independent component analysis and experimental validation》(《Journal of Vibration and Acoustics-Transactions of The ASME》2014, Vol.136, No.4)等论文。 E-mail: chengw@mail.xjtu.edu.cn