A Finite Volume Unstructured Mesh Method for Fractional-in-space Allen-Cahn Equation

(1.School of Mathematics and Statistics,Henan University,Kaifeng,475004,China;Institute of Applied Mathematics,Henan University,Kaifeng,475004,China;Laboratory of Data Analysis Technology,Henan University,Kaifeng,475004,China;2.School of Mathematical Sciences,Queensland University of Technology,GPO Box 2434,Brisbane,Qld.4001,Australia)

§1.Introduction

Proposed firstly by Leibniz in 1695,the concept of fractional calculus has been extended over the years,with non-integer order derivatives being the main characteristic of fractional differential equations(FDEs).As a powerful tool to model the non-loacality and spatial heterogeneity inherent in many real-word problems,the application and computation of FDEs have been increasingly attracting much focus.Fractional models are increasingly used to describe the memory and transmissibility of many kinds of materials,such as chemical and contaminant transport in heterogeneous aquifers in water resources[1−3].Due to the relationship with certain option pricing mechanisms and heavy tailed stochastic processes,FDEs are also used in finance.What’s more,in physics and chemistry,specially in nuclear magnetic resonance and magnetic resonance imaging,the fractional Bloch equation provides an opportunity to describe numerous experimental situations involving heterogeneous porous or composite materials[4−5].

Unfortunately,it is impossible to obtain the analytical solutions for most of FDEs,except some special,simple(usually linear)fractional models.Therefore,numerical solution techniques are preferred to solve more general fractional models[6−17],which stimulate the demand for efficient solution techniques for providing rapid insight and visualisation into solution behaviors.Although finite difference methods, finite element methods,spectral methods, finite volume methods or even mesh-free methods have been proposed for solving FDEs,the high expense of computation hampers the development of these methods.Recently,Yang and Moroney et al.[18−22]and Burrage et al.[23−24]used Krylov subspace methods for computing matrix functions to solve fractional Laplacian equations.Moroney[20]and Wang[25]used Krylov subspace methods to solve the two-sided space-fractional diffusion equation in one dimension,with the former authors considering nonlinear problems and the latter authors considering linear problems with an advection term.In many of these papers,preconditioning has been a common theme,since it is well known that Krylov subspace methods generally require an effective preconditioner in order to perform satisfactorily.Yang et al.[19−22]developed preconditioners based on eigenvalue deflation.Burrage et al.[23]considered both algebraic multigrid and incomplete LU preconditioning.Moroney and Yang[20]developed a banded preconditioner.Especially,Yang et al.[18]introduced a finite volume scheme with proconditioned Lanczos method as an attractive and high-efficiency approach for solving two-dimensional fractional-in-space reaction diffusion equations.This method is very efficient for computing FDEs and it can be used for various kinds of nonlinear reaction-diffusion equations.

Based on Yang’s method,the detailed numerical solution of the fractional-in-space Allen-Cahn(FISAC)equation[24]with a finite volume unstructured triangular mesh method on different domains including irregular domains will be discussed in this paper.The considered FISAC equation takes the following form:

whereKαis a small positive constant,Ω⊂R2is a bounded domain andf(u)=u−u3is the nonlinear source term,u=u(x,y,t).Fractional-in-space Allen-Cahn equation containing a very strong nonlinear source term and small perturbation shows metastability and a quartic double well potential.Using a finite volume unstructured triangular mesh method,the present paper solves the two-dimensional FISAC equation with homogeneous Neumann boundary condition(shown in(1.3))on different irregular domains.The efficiency of the computation and usage on irregular domains will be presented during the following numerical simulation.

§2.A Finite Volume Unstructured Mesh Numerical Scheme on Arbitrary Irregular Domains

Over the last decades, finite volume based-unstructured mesh(FVUM)approaches have in some ways been used for computational fluid dynamics,which overcome the structured nature of the original control volume method[26−29].This paper mainly used the vertex-centred FVUM method not the cell-centred method.The former method had been used by Baliga and Patankar[30],Perr’e and Turner[31]for studying the drying of porous media such as wood.In a discrete solution procedure,the solution domain is subdivided into smaller regions and nodes are distributed throughout the domain,the connections between the nodes and the subregions is known as a mesh.For the vertex-centred approach only the basic elements are considered,which are three-node triangles in this work.Considering the domain Ω,the finite element mesh discretises it into a set of non-overlapping convex polygons,called elements,such thatwhereW={ω1,ω2,···,ωnω}is the set of all elements,andnωis the number of elements,in the mesh.The set of all the vertices of the elements,which are called nodal points,is labelledP={p1,p2,···,pnp}.The set of all edges,which are one-dimensional line segments connecting the nodal points of elements,is labelledD={d1,d2,···,dnd},wherendis the number of edges on the domain.

According to the matrix transfer technique[32],the finite volume discretization of(1.1)is to be derived beginning from the non-fractional equation

The above equation can be rewritten as:

In the solution domain,each node is associated with one control volume(CV),shown by the gray domain surrounded with blue lines in Figure 1 and Figure 2.Each surface of the control volume is defined as the vector that joins the centroid of the element to the midpoint of one of its sides,denoted by CF1 and CF2 for example.Consequently,each of the triangular elements is divided into three domains by these control surfaces.These quadrilateral shapes are called sub-control volumes(SCVs).Thus,a control volume consists of the sum of all neighbouring SCVs that surround any given node.The CV is polygonal in shape and can be assembled in a straightforward and efficient manner at the element level.The flow across each control surface must be determined by an integral.The FVUM discretization process is initiated by utilising the integrated form of(2.2).Integrating(2.2)over an arbitrary control volumeViyields:

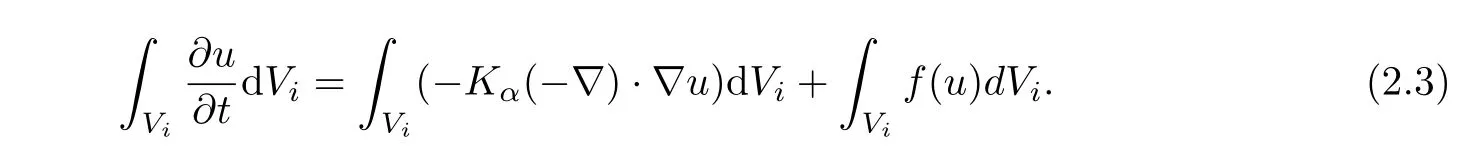
Figure 1:Contruction of a Control Volume around an Internal Node from the Triangular Finite Element.

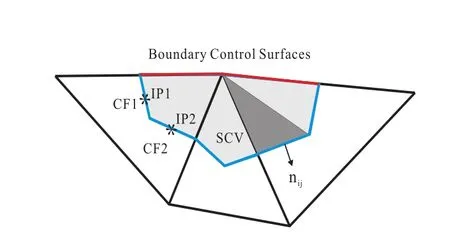
Figure 2:Contruction of a Control Volume around a Boundary Node from the Triangular Finite Element.

Applying the Gauss divergence theorem to the right hand side of Eq.(2.3),

and using a lumped mass approach for the time derivative term gives

where nirepresents the outward unit normal surface vector to the control surface(CF)and an anticlockwise traversal of the finite volume integration is assumed,i.e.,nidΓi=(dy,−dx).In the discrete sense,it can be approximated by ni∆Γi= ∆yi−∆xj;∆xand∆yrepresent thexandycomponents of the SCV face.∆Viand∆Vijare used to denote the area of the control volume and the subcontrol volume surrounding the pointpi,and are evaluated for the vertex case as

wheremiis the total number of SCVs that make up the control volume associated with the nodepi.The integral term in the right hand side of(2.5)is a line integral.It will be approximated by the midpoint approximation for each control surface.To effect this midpoint approximation,the value of the integrand is required at the midpoint of the control surface and it is for these surfaces that the outward normal vector will be specified.

以上分析表明:唯物史观创立及创立之前，人民主体思想一直是其重要的有机组成部分。人民主体思想的深化与变革，必然在一定程度上作用于唯物史观;同时，人民主体思想也因置于科学理论根基之上而更加完备。另外，即使在唯物史观深入发展阶段，对于人们主体思想的探究也将是其核心要件。

The integral term in(2.5)can be rewritten as

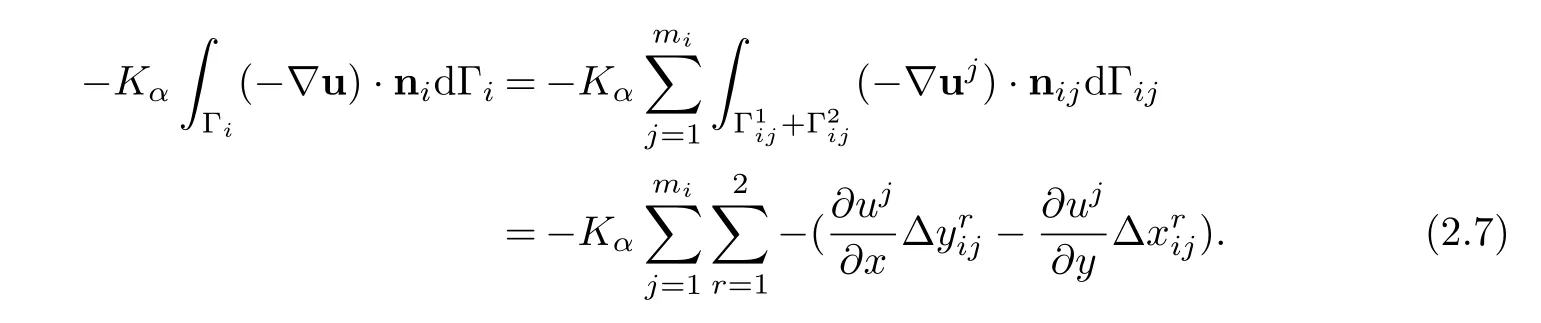
To evaluate the terms in(2.7),one of the triangular elements,ωi,meshed in the solution domain is considered.It has three nodes at the vertices of the triangle.Here,iis the global node and its corresponding control volume number of all the nodes and control volumes.j(1,2,...,mi)andmidenote the number and amount of sub-control volumes consisting of control volumei.For the sake of simplicity,the considered element is noted by∆1,2,3,where 1,2,3 is the local nodal number of the considered element in the counter-clockwise direction.The coordinates values and values ofu(x,y)at the three nodes of the element are noted by(xj,yj),(j=1,2,3)andφj,(j=1,2,3).The variable interpolation function within the element is linear inxandytaken as

or

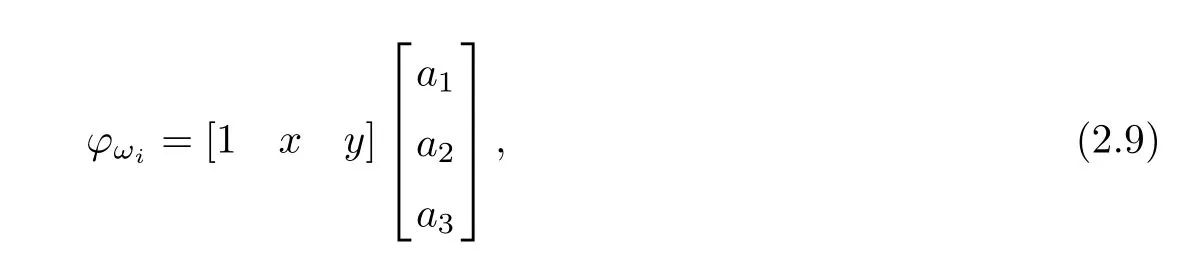
whereaiis the constant to be determined.At the three nodal points,the interpolation function,(2.8)should represent the nodal variablesφ1,φ2,φ3.Therefore,substituting thexandyvalues at each nodal point gives

here,xiandyiare the coordinate values at theithnode of the triangle element anduiis the nodal variable.Inverting the matrix and rewriting(2.10)gives

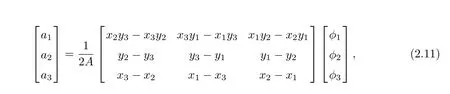
where

The magnitude ofAis the area of the linear triangular element.Its value is positive if the element node numbering is in the counter-clockwise direction.Substitution of(2.11)into(2.9)produces

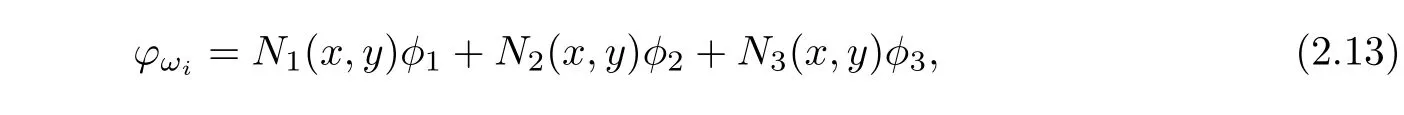
in whichNi(x,y),(i=1,2,3)are the shape functions for linear triangular element and it is given below:

These shape functions also satisfy the conditions

Here,δijis the Kronecker delta.The derivatives ofNiwith respect toxandyare

By using the above linear interpolation shape function,the integral in Eq(2.7)also could be written as

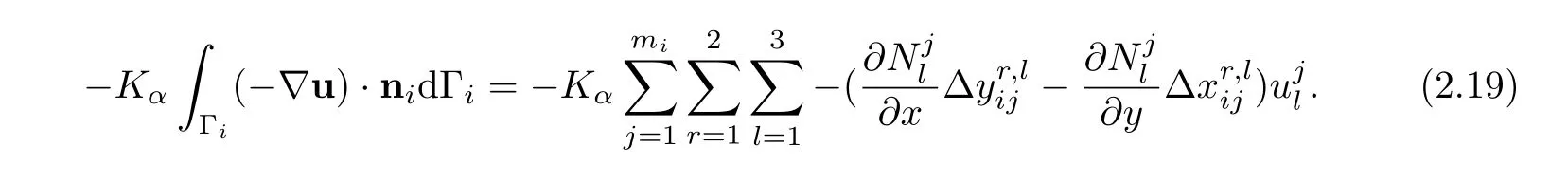
Then

The above discretised equation can be also written in matrical form,

where u=[u1,u2,···,uN]Tis the numerical solution approximatingu(xi,yi,t)at each mesh node(xi,yi).The matrix D=diag(△Vi)is diagonal and represents the contributions from the control volume(CV)areas.The matrix G is sparse,symmetric,positive semi-definite,and represents the contributions from each node towards the total flux through each CV.It is noted that G possesses a single zero eigenvalue owing to the Neumann boundary condition imposed on the problem.

By notifying F=D−1G the above equation could be written as

where F is the finite volume representation of the negative Laplacian(−▽2).

Using the matrix transfer technique,the representation of the fractional Laplacian−(−▽2)α/2is simply−Fα/2since matrix F represents the operator Laplacian(−▽2)with homogeneous boundary conditions under the finite volume discretisation.

With a mixed implicit-explicit scheme,the discretised scheme of the FISAC equation in time can be written as,

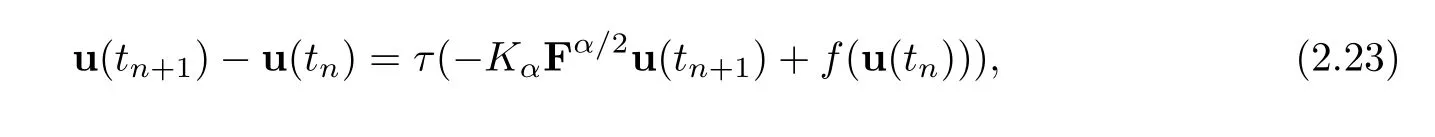
wheretn=nτforn=1,2,...andτis the timestep.With u(tn+1)and u(tn)noted by un+1and un,the above equation can be rewritten as,

where F is the finite volume representation of the negative Laplacian(−▽2),h(F)=(E+τKαFα/2)−1and bn=un+τf(un).

Based on the methods used in Yang et al.[18−19,22]and Burrage et al.[23−24],the matrixfunction-vector producth(F)b could be computed as

§3.Numerical Simulation

Using the above method and programs,the two-dimensional fractional Allen-Cahn equation written in(1.1-1.3)is numerically solved with FVUM on different domains.A random number,obtained fromu0(x,y)=0.1×rand(·)−0.05 on each point is taken as initial values.In order to showcase the efficient usage on irregular domains,the unstructured triangular mesh on an arbitrary irregular domain is considered firstly.Based on the above method and programs,the numerical solution of the fractional-in-space Allen-Cahn equation on an irregular domain is presented in Figure 3.This method of course can be used efficiently on regular domains.The numerical solutions of FISAC equation on a square domain are showcased in Figure 4.According to the diffusion phenomenon,it indicates that for increasingαthe solution changes significantly faster near the center of the interface.The fractional order derivatives could show the more detailed changes during the diffusion process.

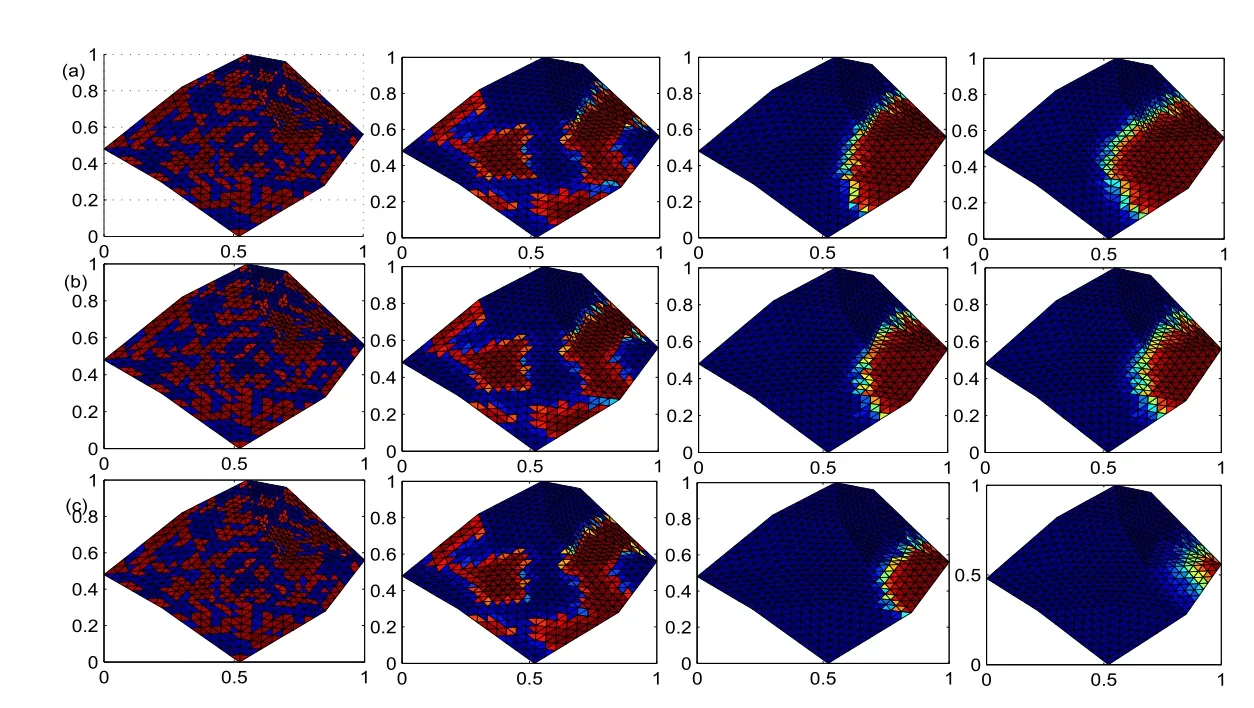
Figure 3:Solution to FISAC Equation with α=1.2,1.5,1.8 and 2.0 on an Arbitrary Irregular Domain at t=30,60 and 100 with Random Initial Values.

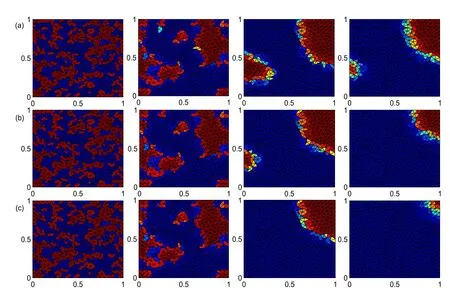
Figure 4:Numerical Solution to FISAC Equation at t=30,t=60 and t=100 with Different Fractional Derivatives α =1.2,1.5,1.8,2 on the Square[0,1.0]×[0,1.0].

§4.Conclusion

In this manuscript,the two-dimensional control volume finite-element computational model is developed for simulating the fractional-in-space Allen-Cahn equation.By using a finite volume spatial discretisation and presenting a preconditioned Lanczos method for FISAC equation,the solution on different domains with unstructured triangular mesh are obtained efficiently.The efficient method discussed in this paper can be used for computing not only FISAC equation but also other fractional-in-space nonlinear reaction-diffusion equations on arbitrary domains(the results not shown here).

[1]ADAMS E E,GELHAR L W.Field study of dispersion in a heterogeneous aquifer:2.Spatial moment analysis[J].Water Resources Research,1992,28(12):3325–3336.

[2]BENSON D A,WHEATCRAFT S W,MEERSCHAERT M M.Application of a fractional advection dispersion equation[J].Water Resources Research,2000,36(6):1403–1412.

[3]MEERSCHAERT M M,BENSON D A,WHEATCRAFT S W.Subordinated advection-dispersion equation for contaminant transport[J].Water Resource Research,2001,37:1543–1550.

[4]YU Qiang.Numerical simulation of anomalous diffusion with application to medical imaging[D].Brisbane:Queensland University of Technology,2013.

[5]WYSS W.The fractional Black-Scholes equation[J].Fractional Calculus and Applied Analysis,2000,3:51–62.

[6]MEERSCHAERT M M,TADJERAN C.Finite difference approximations for fractional advection-dispersion flow equations[J].Journal of Computational and Applied Mathematics,2004,172:65–77.

[7]MEERSCHAERT M M,TADJERAN C.Finite difference approximations for two-sided space-fractional partial differential equations[J].Applied Numerical Mathematics,2006,56:80–90.

[8]MEERSCHAERT M M,SCHEFFLER H P,TADJERAN C.Finite difference methods for two-dimensional fractional dispersion equation[J].Journal of Computational Physics,2006,211(1):249–261.

[9]TADJERAN C,MEERSCHAERT M M.A second-order accurate numerical method for the two-dimensional fractional diffusion equation[J].Journal of Computational Physics,2007,220(2):813–823.

[10]ERVIN V J,ROOP J P.Variational formulation for the stationary fractional advection dispersion equation[J].Numerical Methods for Partial Differential Equations,2006,22(3):558–576.

[11]LIU Qing-xia,LIU Fa-wang,TURNER I,et al.Numerical simulation for the 3D seepage flow with fractional derivatives in porous media[J].Ima Journal of Applied Mathematics,2009,74(2):201–229.

[12]GU Yuan-tongu,ZHUANG Ping-hui,LIU Qing-xia,An advanced meshless method for time fractional diffusion equation[J].International Journal of Computational Methods,2011,08(04):653–665.

[13]LIU Qing-xia,GU Yuan-tong,ZHUANG Ping-hui,et al.An implicit RBF meshless approach for time fractional diffusion equations[J].Computational Mechanics,2011,48(1):1–12.

[14]ZHANG Hong-mei,LIU Fa-wang,ANH V.Galerkin finite element approximation of symmetric spacefractional partial differential equations[J].Applied mathematics and computation,2010,217(6):2534–2545.

[15]LI Xiao-yan,XIANG Jiang-ru,WU Ya-yun.Laplace transform method applied to solve fractional difference equations[J].Chinese Quarterly Journal of Mathematics,2015,1:121–129.

[16]ZHANG Hong-mei,LIU Fa-wang,TURNER I,et al.The numerical simulation of the tempered fractional Black-Scholes equation for European double barrier option[J].Applied Mathematical Modelling,2016,40(11C12):5819-5834.

[17]MA Yan.Analysis of an implicit finite difference scheme for time fractional diffusion equation[J].Chinese Quarterly Journal of Mathematics,2016,1:69–81.

[18]YANG Qian-qian,TURNER I,MORONEY T,et al.A finite volume scheme with preconditioned Lanczos method for two-dimensional space-fractional reaction C diffusion equations[J].Applied Mathematical Modelling,2014,38:3755–3762.

[19]MORONEY T,YANG Qian-qian.A banded preconditioner for the two-sided,nonlinear space-fractional diffusion equation[J].Computers&Mathematics with Applications,2013,66(5):659–667.

[20]MORONEY T,YANG Qian-qian.Efficient solution of two-sided nonlinear space-fractional diffusion equations using fast Poisson preconditioners[J].Journal of Computational Physics,2013,246:304–317.

[21]YANG Qian-qian,TURNER I,LIU Fa-wang,et al.Novel numerical methods for solving the time-space fractional diffusion equation in two dimensions[J].SIAM Journal on Scienti fic Computing,2011,33:1159–1180.

[22]SIMMONS A,YANG Qian-qian,MORONEY T.A preconditioned numerical solver for stiffnonlinear reaction C diffusion equations with fractional Laplacians that avoids dense matrices[J].Journal of Computational Physics,2015,287:254–268.

[23]BURRAGE K,NICHOLAS H,KAY D.An efficient implicit FEM scheme for fractional-in-space reaction diffusion equations[J].SIAM Journal on Scientific Computing,2012,34:A2145–A2172.

[24]BUENO-OROVIO A,KAY D,BURRAGE K.Fourier spectral methods for fractional-in-space reaction diffusion equations[J].BIT Numerical Mathematics,2014,54(4):937–954.

[25]WANG Kai-xin,WANG Hong.A fast characteristic finite difference method for fractional advection C diffusion equations[J].Advances in Water Resources,2011,34(7):810–816.

[26]Chow P M.Control volume unstructured mesh procedure for convection-diffusions solidification processes[D].London:University of Greenwich,1993.

[27]LIU Fa-wang,TURNER I W,ANH V V.An unstructured mesh finite volume method for modelling saltwater intrusion into coastal aquifers[J].Korean Journal of Computational&Applied Mathematics,2002,9:391–407.

[28]LIU Fa-wang,ANH V V,TURNER I W,et al.A finite volume simulation model for saturated–unsaturated flow and application to Gooburrum[J].Applied Mathematical Modelling,2006,30(4):352–366.

[29]CUMMING B D.Modelling sea water intrusion in coastal aquifers using heterogeneous computing[D].Brisbane:Queensland University of Technology,2012.

[30]BALIGA B R,PATANKAR S V.Elliptic System:Finite Element I.Handbook of Numerical Heat Transfer[M],Wiley,1988.

[31]PERRE P,TURNER I W.Trans Pore:a generic heat and mass transfer computational model for understanding and visualising the drying of porous media[J].Invited paper,Drying Technology Journal,1999,17(7):1273–1289.

[32]ILIC M,LIU Fa-wang,TURNER I W,et al.Numerical approximation of a fractional-in-space diffusion equation(II)with nonhomogeneous boundary conditions[J].Fractional Calculus&Applied Analysis,2006,9(4):333–349.