Global Existence,Asymptotic Behavior and Uniform Attractors for Damped Timoshenko Systems

(1.College of Science,Donghua University,Shanghai 201620,China;2.Department of Applied Mathematics,Donghua University,Shanghai 201620,China)

§1.Introduction

We consider the following Timoshenko system with a frictional damping in one equation

where the functionsϕ,ψdepending on(t,x)∈(0,∞)×(0,L)model the transverse displacement of a beam with reference configuration(0,L)⊂R and the rotation angle of a filament respectively.Denotingρ1,ρ2,das positive constants and the given non-linear functionsσ1,σ2will be assumed to satisfy forj=1,2

whereκand b are positive constants.A simple example forσ1with essential nonlinearity in the first variable is given by

and the nonlinear part corresponding to a vibrating string.Then the linearized system consists of

the common linear Timoshenko system,cp.[1,21].

The boundary conditions both for the linear and the nonlinear system will be given for t≥0 by

Additionally one has initial conditions

Ifd=0,then(1.5)～(1.6)build a purely hyperbolic system where the energy is conserved and a solution,respectively the energy,does not decay at all,of course.Moreover,the system(1.1)～(1.2)is expected to develop singularities in finite time because of its typical nonlinear hyperbolic character.

Soufyane[219]proved for the boundary conditionsφ=ψ=0,also for positived=d(x),that the linearized system is exponentially stable if and only if

holds,that is,if and only if the wave speeds associated to(1.5)～(1.6),respectively,are equal.In[11]we investigated Timoshenko systems where the dissipation arises not through a fricitional damping but through the impact of heat conduction being coupled to the differential equation(1.2)forψ.

Energy methods and spectral analysis arguments will be used that will have to combine methods previously used for Timoshenko systems as in[1],for systems with Kelvin-Voigt damping[3]and for nonlinear systems as described for Cauchy problems in[20].It is well-known(see,e.g.,[2,6,9])that the energy of one-dimensional linear thermoelastic system associated with various types of boundary conditions decays to zero exponentially.For the multi-dimensional case,we have the pioneering work of Daformos[5],in which he proved an asymptotic stability result.The uniform rate of decay for the solution in two or three dimensional space was obtained by Jiang,Rivera and Racke[22]in a special situation like radial symmetry.Lebeau and Zuazua[8]proved taht the decay rate is never uniform when the domain is convex.

Especially,Qin[14-15]established the global existence,asymptotic behavior of smooth solutions under more general constitutive assumptions,and more recently,Qin[17]has further improved these results and established the global existence,exponential stability and the existence of maximal attractors inHi(i=1,2,4).As for the existence of global(maximal)attractors of the Navier-Stokes equations,we refer to the works by Zheng and Qin[24],Qin and Muoz Rivera[19],Qin,Ma,Cavalcanti,and Andrade[18]and Qin[16].Our aim in this work is to investigate(1.5)～(1.8)and prove the global well-posedness of the thermoelastic system and establish its uniform attractors.The paper is organized as follows.In Section 2,we shall use the semigroup method to prove an existence and uniqueness result.Then,in Section 3,using the multiplicative method and some arguments from[12,23],we state and prove asymptotic behavior of solutions.We also prove the existence of the uniform attractor in Section 4.Moreover,in Section 5 the semilinear case is firstly considered.

§2.Global Well-posedness

We rewrite the linearized initial-boundary value problem(1.5)～(1.8)as the first-order system foru:=(u1,u2,u3,u4)′andu1=ϕ,u2=ϕt,u3=ψ,u4=ψt.

We are now in a position to state our main theorems.

Theorem 2.1Suppose thatf(x,t),g(x,t)∈C1([0,+∞),L2(0,L)),then for anyϕ0∈H2(0,L),ϕ1∈(0,L),ψ0∈H2(0,L),ψ1∈H1(0,L)and satisfying initial boundary conditions,problem(1.5)～(1.6)admits a unique classical solution(ϕ(x,t),ψ(x,t)),such that

In order to complete the proof of Theorem 2.1,we need the following lemmas.For an abstract initial value problem

whereAis a maximal accretive operator defined in a dense subsetD(A)of a Banach spaceH.We have

Lemma 2.1LetAbe a linear operator defined in a Hilbert spaceH,A:D(A)⊂H→H.Then the necessary and sufficient conditions forAbeingm-accretive are

(i)Re(Ax,x)≥0 for any x∈D(A),

(ii)R(I+A)=H.

ProofSee,e.g.,Zheng[23].

Lemma 2.2Assume thatF(t)=0 andAism-accretive in Banach spaceH,y0∈D(A).Then problem(2.10)has a unique classical solutiony(t),such that

ProofSee,e.g.,Zheng[23].

Lemma 2.3Assume thatAism-accretive in a Banach spaceHand

Then problem(2.10)has a unique classical solutiony(t)such that

which can be expressed as

ProofSee e.g.,Zheng[23].

Proof of Theorem 2.1By Lemma 2.1,(Au,u)≥0,we can know thatAis a maximal monotone operator(see also[23]).By the assumptions,we have(ϕ0,ϕ1,ψ0,ψ1)T∩D(A),then by Lemma 2.3,we complete the proof.

§3.Uniform Stability

In this section,we shall state and prove our decay results.To this end,we need now to establish several lemmas.

Lemma 3.4Let(ϕ,ψ)be the solution of(1.5)～(1.8).Then the energy function defined by

satisfies,for anyε0＞0,

with some constantC1＞0 andC1being independent of initial data.

ProofMultiplying(1.5)～(1.6)byϕt,ψtrespectively,and integrating over(0,L)and summing up,we obtain

Using Hölder’s inequality and Young’s inequality,we obtain

The proof is complete.

Lemma 3.5Let(ϕ,ψ)be the solution of(1.5)～(1.8).Then the functionalF1defined by

satisfies,anyε1＞0.

ProofBy a direct computing and using equation(1.5).Then by Young’s inequality,we obtain for anyε1＞0.

Thus,the proof is complete.

Lemma 3.6Let(ϕ,ψ)be the solution of(1.5)～(1.8).Then the functionalF2defined by

satisfies,for anyε2＞0,

ProofBy a direct computing and using equation(1.6).Then by Young’s inequality,we obtain for anyε2＞0,

Thus,the proof is complete.

Lemma 3.7Let(ϕ,ψ)be the solution of(1.5)～(1.8).Then the functionalF3defined by

and by a direct computing and using equation(1.5)～(1.6),we have

Moreover,

We conclude for

Then by Young’s inequality,we obtain for anyε3＞0,

Thus,the proof is complete.

Lemma 3.8Suppose thaty(t)∈C1(R+),y(t)≥0,∀t＞0 and satisfies

where 0≤λ∈L1(R+)andC0is a positive constant.Then we have

Furthermore,

withC2＞0,α＞0 being constants.

with a constantC4＞0.

ProofSee,e.g.,[13].

Theorem 3.2Let(ϕ0,ϕ1,ψ0,ψ1)T∈D(A),(ϕ(x,t),ψ(x,t))is the solution of(1.5)～(1.8)andf(x,t),g(x,t)∈C1([0,+∞),L2(Ω)).Then we have

If further

withC0＞0 andα0＞0 being constants,then there exist positive constantsM,αsuch that the energyE(t)satisfies

with constantsC′＞0,p＞1,then there exists a constantC∗＞0 such that

ProofForε＞0,we define a Lyapunov functionalLas follows

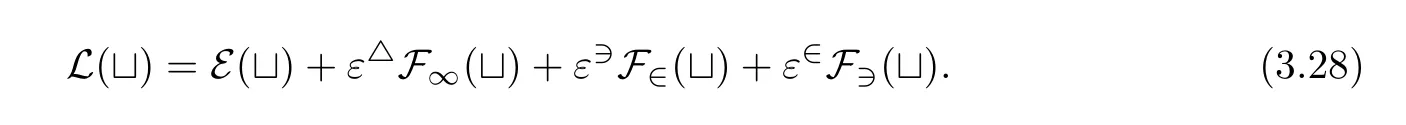
By using(3.2),(3.6),(3.9),(3.12),we get

for some constantC′＞0 andC′being independent of initial data.

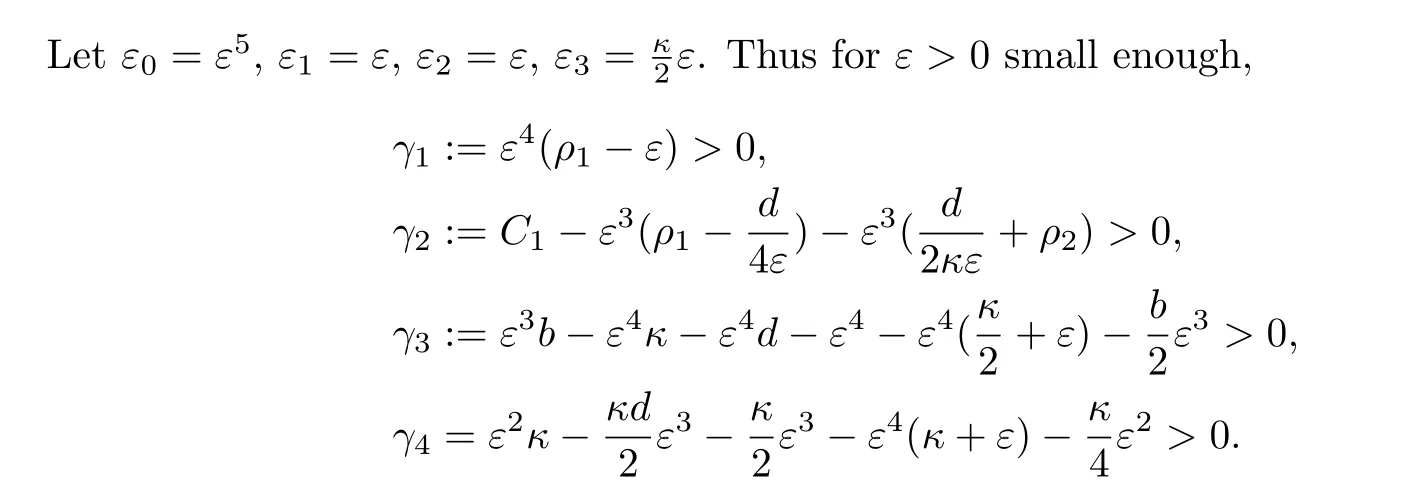
So we arrive at

By Poincar´e’s inequality,we have

for a constantγ′＞0.

On the other hand,we see(e.g.,[10])thatLis equivalent toE(t),i.e.,L～E.

Hence we derive from(3.30)that there exists a constantγ＞0,such that

Applying Lemma 3.5 to(3.31),we can conclude(3.23),(3.25),(3.27).

§4.Uniform Attractors

In this section,we shall establish the existence of uniform attractors for non-autonomous system(1.5)～(1.8).SettingRτ=[τ,+∞),τ≥0,we consider the following system.

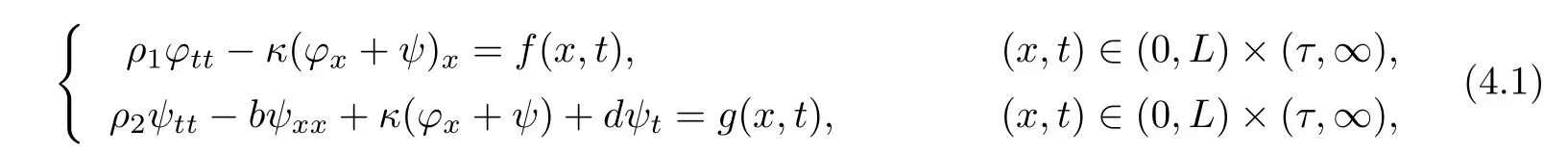
together with the initial conditions

and boundary conditions

The energy of problem(4.1)is given by

For any(ϕτ,ϕ1τ,ψτ,ψ1τ)∈H∞and anyF∈E,we define fort≥τ,τ≥0,

where(ϕ(t),ϕt(t),ψ(t),ψt(t))solves the problem(4.1).Our result concerns the uniform attractor inH∞,we define the hull ofF0∈Eas

where[·]Edenotes the closure in Banach spaceE.We note that

Theorem 4.3Let Σ=[F0(t+h)|h∈R+]X,whereF0∈Xis an arbitrary but fixed symbol function.Then for anyF∈Σ and for any(ϕτ,ϕ1τ,ψτ,ψ1τ)∈H1,τ≥0,problem(4.1)admits a unique global solution(ϕ(t),ϕt(t),ψ(t),ψt(t))∈H1,which generates a unique semi-processes{UF(t,τ)}(t≥τ≥0)onH1of a two-parameter family of operators,such that for anyt≥τ≥0,

First,we shall establish the family of semi-processes{Uσ(t,τ)}has a bounded uniformly absorbing set given in the following theorem.

Theorem 4.4Under the assumption(4.4),the family of processesUF(t,τ)(F∈Σ,t≥τ≥0),corresponding to(4.1)～(4.3)has a bounded uniformly(w.r.t.F∈Σ)absorbing setB0inH1.

ProofSimilarly to the proof of Theorem 3.1,we can derive

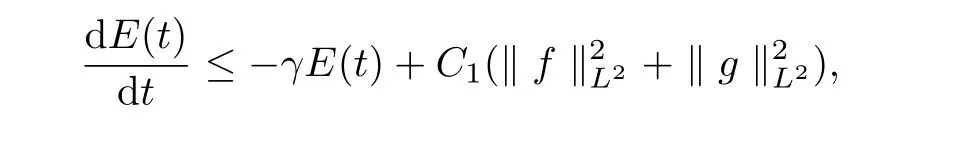
whereγ,C1are two positive constants andC1being independent of initial data.

In the following,Cdenotes a general positive constant independent of initial data,which may be different in different estimates.

Obviously,we have

Applying Lemmas in V V Chepyzhov and M I Vishik[4]to(4.8),we conclude

Now for any bounded setB0⊆H,for any(ϕτ,ϕ1τ,ψτ,ψ1τ)∈B0,τ≥0,there exists a constantCB0＞0 such thatE(τ)≤CB0≤C.Taking

Without loss of generality,we assume thatρ1=ρ2=b=κ≡1.Multiplying the first and second equations of(4.11)byω(t),λ(t),respectively,integrating the results over(0,L)and summing them up,we arrive at

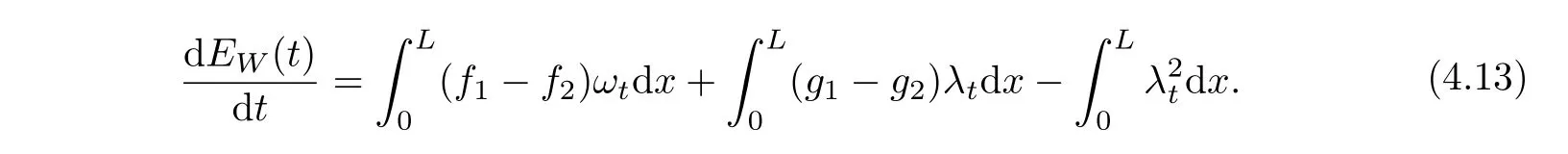
Integrating over[σ,T](0≤σ≤T)and using Young’s equality,we get

Integrating over[0,T]with respect toσ,we obtain that

we derive

whereCM=C(T,τ,γ)is a positive constant.

By Young’s inequality and Poincaré’s inequality,we also know that

In the sequel,we shall state and prove the uniformly(w.r.t.F∈Σ)asymptotic compactness inH∞,which is stated in the following theorem.

Theorem 4.5Assume that F satisfies(4.4),then the family of semi-processes{UF(t,τ)}(F∈Σ,t≥τ≥0),corresponding to(4.1)is uniformly(w.r.t.F∈Σ)asymptotically compact inH1.

By Theorem 4.2 in[22],we can conclude the family of semi-processes{UF(t,τ)},corresponding to(4.1),is uniformly asymptotically compact inH1.

The proof is now complete.

Then we can easily derive the existence of the uniform attractor given in the following theorem.

Theorem 4.6Assume that F satisfies(4.4),then the family of semi-processes{UF(t,τ)}(F∈Σ,t≥τ≥0),corresponding to problem(4.1),has a uniformly(w.r.t.F∈Σ)compact attractorA±.

ProofTheorems 4.2 and 4.3 imply the existence of a uniform attractor immediately.

§5.Semilinear Timoshenko Systems

In this section,we shall consider the following system

In order to get our results,we have to introduce some basic lemmas.We are concerned with the initial value problem for the semilinear evolution equation

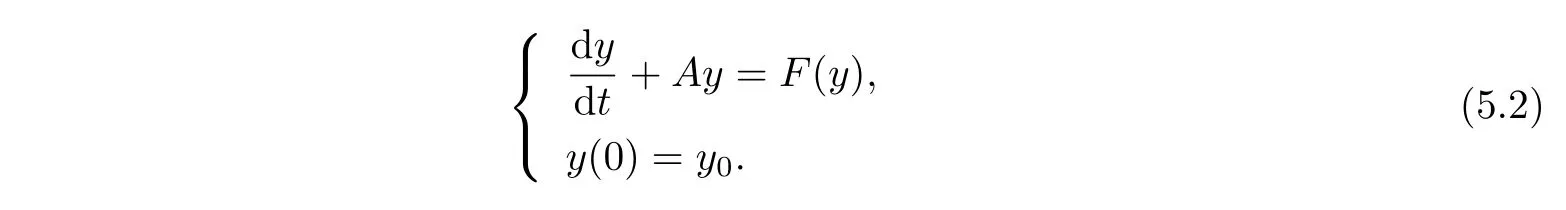
WhereAis a maximal accretive operator from a dense subsetD(A)in a Banach spaceHintoH,andFis a nonlinear operator fromHintoH,we have

Theorem 5.7Suppose thatf,g∈C1(R3,R)and▽f,▽gis uniformly bounded,then for anyϕ0∈H2(0,L),ϕ1(0,L),ψ0∈H2(0,L),ψ1∈H1(0,L),ψx(0,t)=ψx(L,t)=0,problem(5.1)admits a global mild solution(ϕ(x,t),ψ(x,t)),such that

Theorem 5.8Suppose thatf,g∈C1(R3,R).Then for anyϕ0∈H2(0,L),ϕ1(0,L),ψ0∈H2(0,L),ψ1∈H1(0,L),ψx(0,t)=ψx(L,t)=0,problem(5.1)admits a unique global classical solution(ϕ(x,t),ψ(x,t))on[0,Tmax),such that

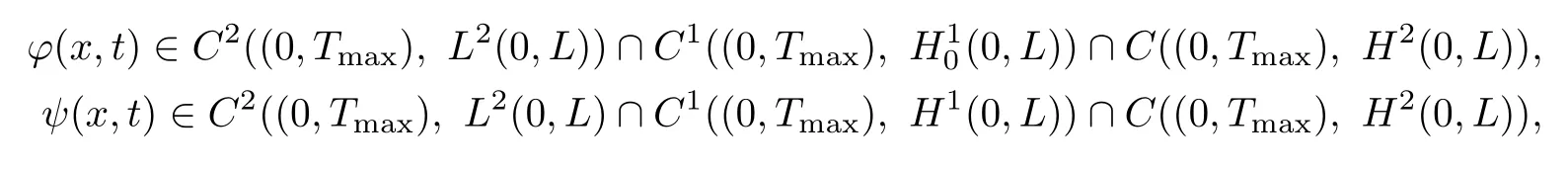
whereTmaxis the maximal existence interval of solution.

Moreover,there is an alternative,

(i)EitherTmax=+∞,i.e.,the solution is a global one or

(ii)Tmax＜∞and

i.e.,the solution blows up in a finite time.

ProofSame as the proof of Theorem 5.1,we haveH,D(A)andFis a nonlinear operator fromHintoH,F∈C1(H,H).Then we shall prove thatFsatisfies the global Lipschitz condition,in fact,for allU=(u1,u2,u3,u4),V=(v1,v2,v3,v4)∈H,‖U‖H≤R,‖V‖H≤R,whereRis an arbitrarily positive constant.

Then we get

Thus from[23],we complete the proof.

[1]AMMAR KHODJA F,BENABDALLAH A,MU˜NOZ RIVERA J E,et al.Energy decay for Timoshenko systems of memory type[J].J Differential Equations,2003,194(1):82-115.

[2]BURNS J A,LIU Zhuang-yi,ZHENG Song-mu.On the energy decay of a linear thermoelastic bar[J].J Math Appl,1993,179:574-591.

[3]CHEN Shu-ping,LIU Kang-sheng,LIU Zhuang-yi.Spectrum and stability for elastic systems with global or local Kelvin-Voigt damping[J].SIAM J.Appl.Math.1998,59:651-668.

[4]CHEPYZHOV V V,VISHIK M I.Attractors of Equations of Mathematical Physics[C].Island:Rhode 2002.

[5]DAFERMOS C M.On the existence and the asymptotic stability of solutions to teh equations of linear thermoelasticty[J].Arch Rat Mech Anal,1968,29:241-271.

[6]HANSEN S W.Exponential energy decay in a linear thermoelastic rod[J].J Math Anal Appl,1992,167:429-422.

[7]JIANG Song,MU˜NOZ RIVERA J E,RACKE R.Asymptotic stability and global existence in thermoelasticity with symmetry[J].Quart Appl Math,1998,56(2):259-275.

[8]LEBEAU G,ZUAZUA E.Sur la d´ecroissance non uniforme de l’´energie dans le syst`eme de la thermoelastict´elin´eaire[J].C R Acad Sci Paris S´er I Math,1997,324:409-415.

[9]LIU Zhuang-yi,ZHENG Song-mu.Exponential stability of the semigroup associated with a thermoelastic system[J].Quart Appl Math,1993,51:535-545.

[10]MESSAOUDI S A,SAID-HOUARI B.Energy decay in a Timoshenko-type system of thermoelasticity of type III[J].J Math Anal Appl,2008,348(1):298-307.

[11]MU˜NOZ RIVERA J E,RACKE R.Mildly dissipative nonlinear Timoshenko systems global existence and exponential stability[J].J Math Anal Appl,2002,276:248-278.

[12]MUSTAFA M I.Exponential decay in thermoelastic systems with boundary delay[J].Abstract DiffEquat Appl,2011,2(1):1-13.

[13]OLIVEIRA J C,CHAR˜AO R C.Stabilization of a locally damped thermoelastic system[J].Comput Appl Math,2008,27(3):319-357.

[14]QIN Yu-ming.Asymptotic behavior for global smooth solution to a one-dimensional nonlinear thermoviscoelastic system[J].J Partial Differ Equ,1999,12:111-134.

[15]QIN Yu-ming.Global existence and asymptotic behavior of solution to the system in one-dimensional nonlinear thermoviscoelasticity[J].Quart Appl Math,2001,59:113-142.

[16]QIN Yu-ming.Universal attractor inH4for the nonlinear one-dimensional compressible Navier-Stokes equations[J].J.Differential Equations,2004,207:21-72.

[17]QIN Yu-ming.Exponential stability and maximal attractors for a one-dimensional nonlinear thermoviscoelasticity[J].IMA J Appl Math,2005,70:1-18.

[18]QIN Yu-ming,MA T F,CAVALCANTI M M,ANDRADE D.Exponential stability inH4for the Navier-Stokes equations of compressible and heat conductive fluid[J].Commun Pure Appl Anal,2005,4:635-664.

[19]QIN Yu-ming,MUN˜OZ RIVERA J E.Universal attractors for a nonlinear one-dimensional heat-conductive viscous real gas[J].Proc R Soc Edinb A,2002,132:685-709.

[20]RACKE R.Lectures on nonlinear evolution equations,initial value problems[M].Aspects of Mathematics E19,Friedr.Vieweg&Sohn,Braunscheig/Wiesbaden,1992.

[21]SOUFYANE A.Stabilisation de la poutre de Timoshenko[J].C R Acad Sci Paris,S´er.1999,328:731-734.

[22]SUN Chun-you,CAO Dao-min,DUAN Jin-qiao.Uniform attractors for non-autonomous wave equations with nonlinear damping[J].Soc Indu Appl Math,AMS,2006,6(2):293-318.

[23]ZHENG Song-mu.Nonlinear Evolution Equations[M].USA:CRC Press,2004.

[24]ZHENG Song-mu,QIN Yu-ming.Universal attractors for the Navier-Stokes equations of compressible and heat conductive fluids in bundled annular domains inRn[J].Arch Rat Mech Anal,2001,160:153-179.