Global Existence and Asymptotic Behavior of Non-autonomous Timoshenko Systems

(1.College of Science,Donghua University,Shanghai 201620,China;2.Department of Applied Mathematics,Donghua University,Shanghai 201620,China)

§1.Introduction

Given a real intervalJ=[0,l],we consider the following Timoshenko system

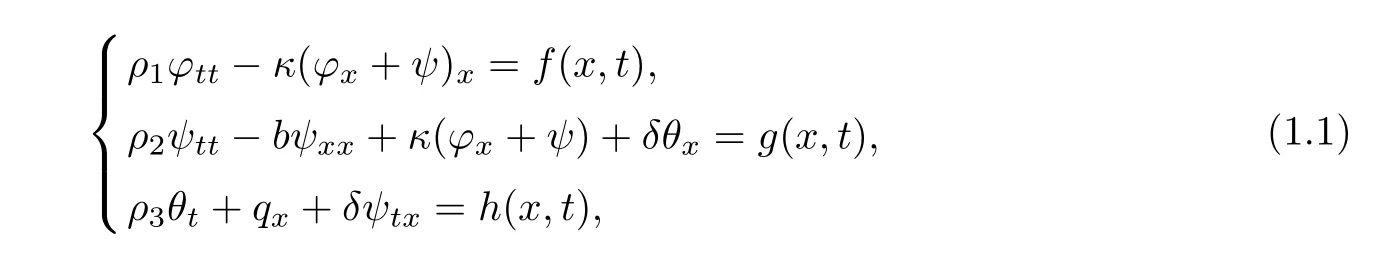
whereρ1,ρ2,ρ3,κ,b,δ,β＞0 are fixed constants.Functionsf,g,hare known functions specified later on,and the unknown variables

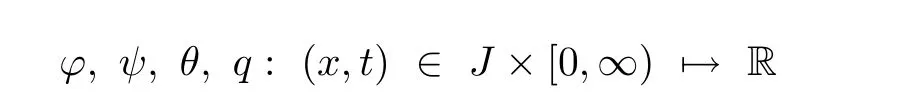
represent the transverse displacement of a beam,the rotation angle of a filament,the relative temperature and the heat flux vector,respectively.

We associate(1.1)with the initial conditions

and boundary conditions

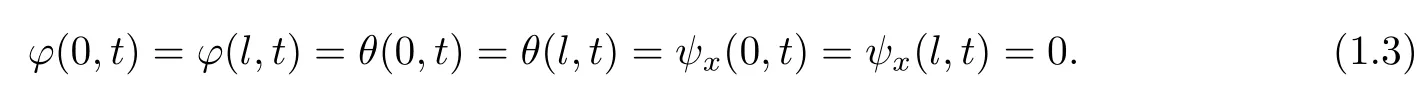
In what follows,〈.,.〉and‖.‖are the standard inner product and norm on the Hilbert spaceL2(J).We introduce the Hilbert subspace

of zero-mean functions,along with the Hilbert spaces

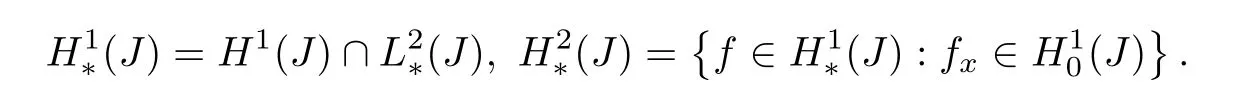
Both endowed with the gradient norm,due to the Poincare inequality.

Now we would like to recall some related results.According to the thermal laws for the heatflux,there exist three relations betweenqandθ.Reference Rivera[2]analyzed the exponential stability of the resulting Timoshenko-Fourier system,giving a sufficient condition0.As to the Cattaneo thermal law,Sare[8]proved that exponential stability can never occur when given a co-called stable numberχ=0.However,Santos[7]gave a new stability number

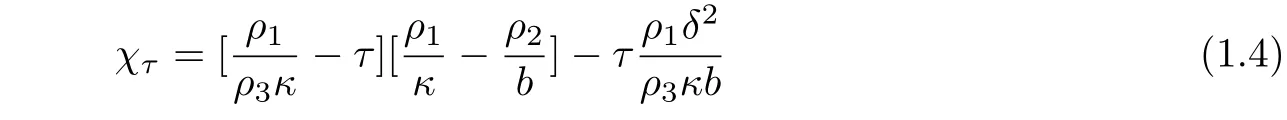
and proved that the system can be exponentially stable if and only ifχτ=0 via linear semigroup methods.Under the Gurtin-Pipkin thermal law,Dell’Oro[3]built a stability number

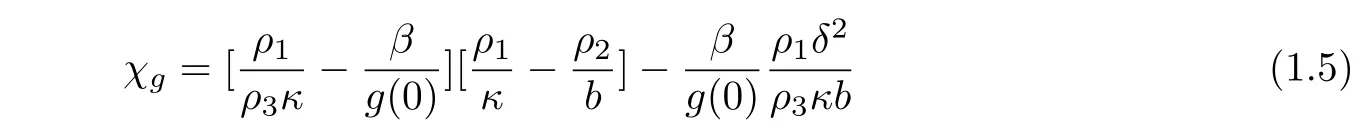
and showed that the system can be exponentially stable if and only ifχg=0 via linear semigroup techniques.A further interesting model,midway between the Fourier and Gurtin-Pipkin one obtained by assuming the Coleman-Gurtin law for the heat flux Coleman[2]was studied in Dell’Oro[3]as well.However,all the results described above are homogeneous models and this paper will study the non-autonomous situations.

§2.Global Existence of Linear Timoshenko System

Under the Cattaneo thermal law,the system(1.1)can be transferred to(see Santos[7])

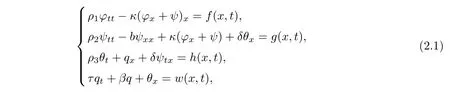
whereτ,β＞0 is constants.

In order to state our main result,we may first rewrite problem(2.1)in an abstract form.Furthermore,we can use the semigroup method to deduce the well-posedness of this system.We produce new dependent variablesThen system(2.1)and(1.2)are converted to the following abstract ODE

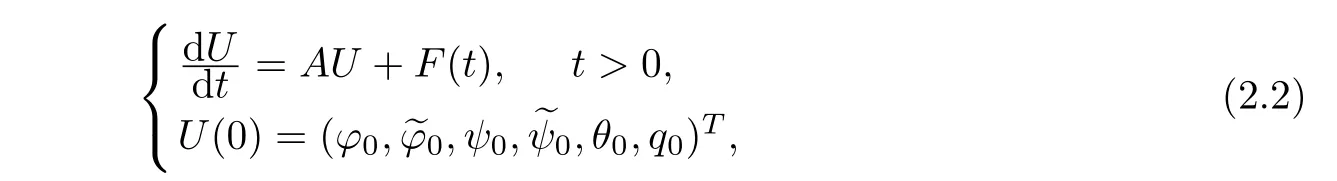
where

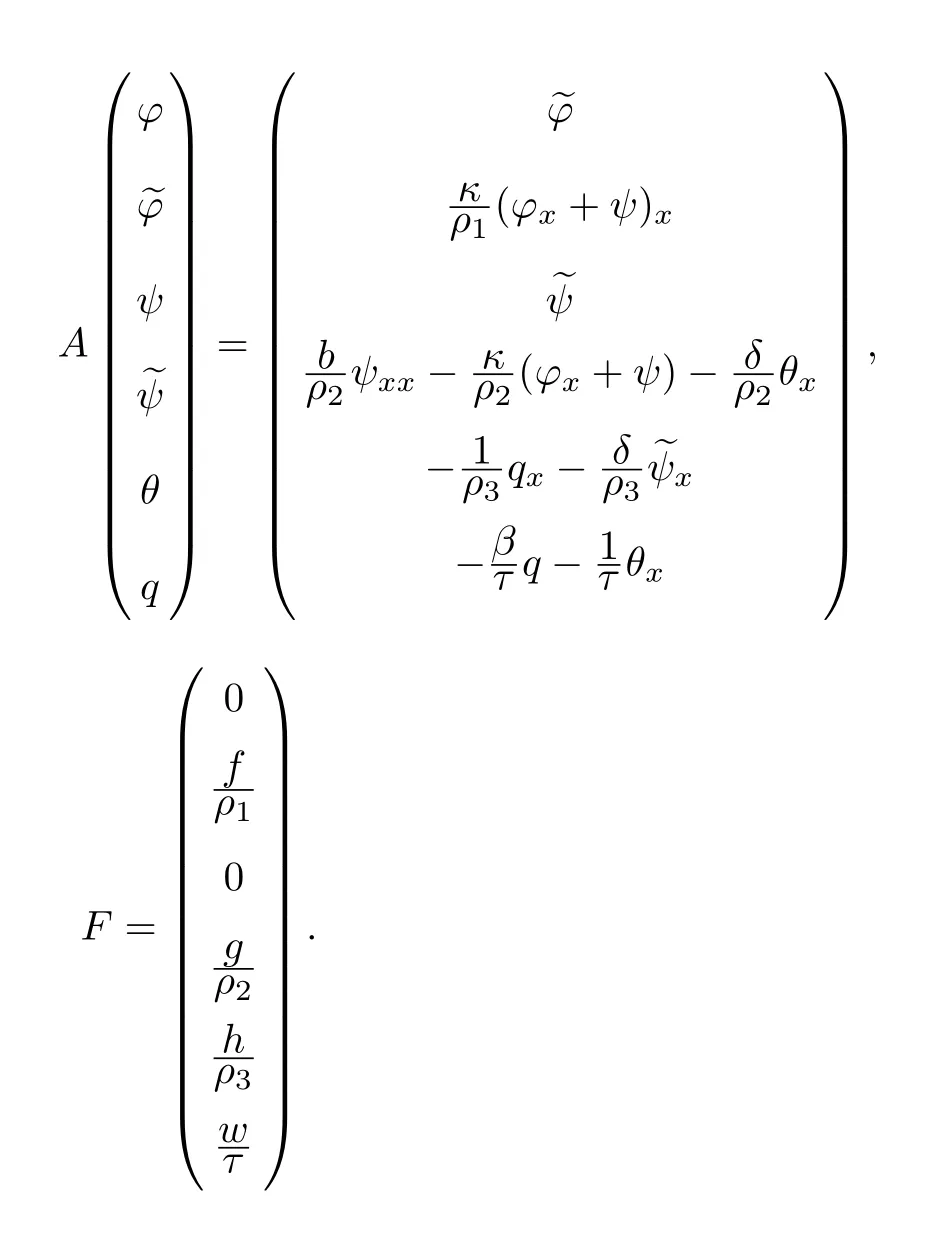
We define

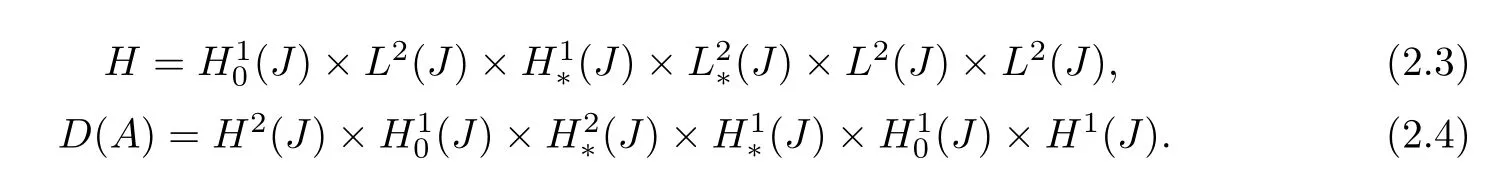
ThusA:D(A),→His a linear operator.

ForU=(u1,u2,u3,u4,u5,u6),V=(v1,v2,v3,v4,v5,v6)∈H,we equipHwith the inner product

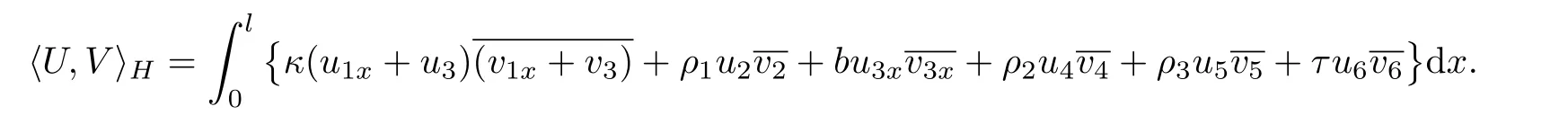
Now we state the following existence and regularity result.

Theorem 2.1Suppose thatf∈C1([0,∞),L2(J)),g∈C1([0,∞)(J)),h∈C1([0,∞),L2(J)),w∈C1([0,∞),L2(J))andϕ0∈H2(J),ψ0(J),θ0(J),q0∈H1(J).Then problem(2.1)admits a unique classical solution(ϕ,ψ,θ,q)such that

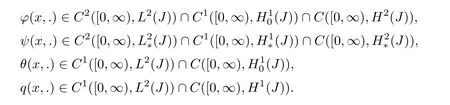
In order to complete the proof of Theorem 2.1,we need the following lemmas.For an abstract initial value problem

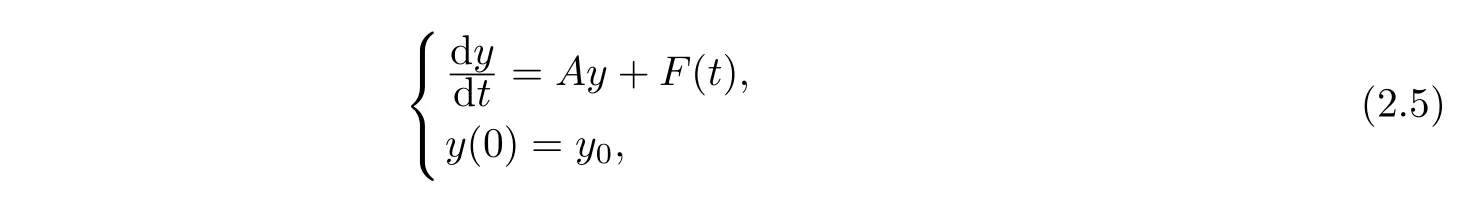
whereAis a maximal accretive operator defined in a dense subsetD(A)of a Banach spaceH,we have following lemmas.

Lemma 2.1LetAbe a linear operator defined in a Hilbert spaceH,A:D(A)⊂H→H.Then the necessary and sufficient conditions forAbeing maximal accretive are

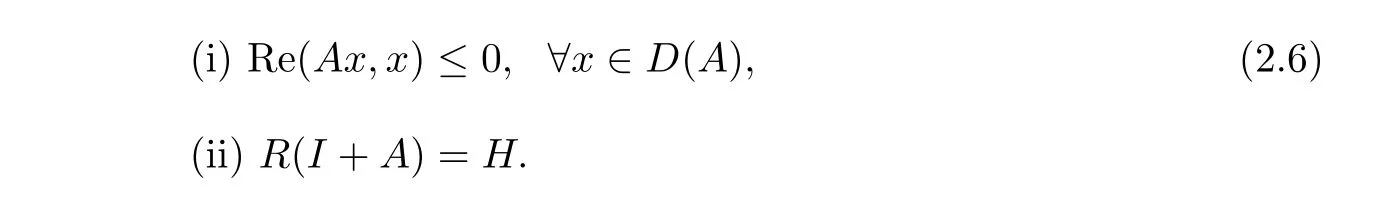
ProofSee,e.g.,Zheng[9].

Lemma 2.2AssumeAis m-accretive in Banach spaceHand

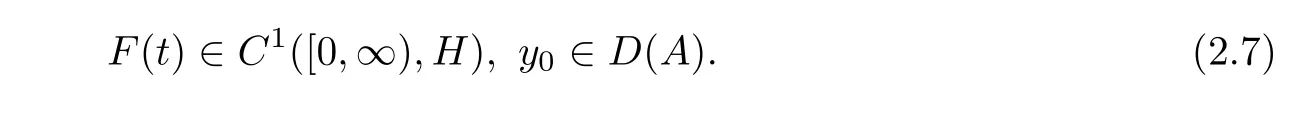
Then problem(2.5)has a unique classical solutiony(t)such that

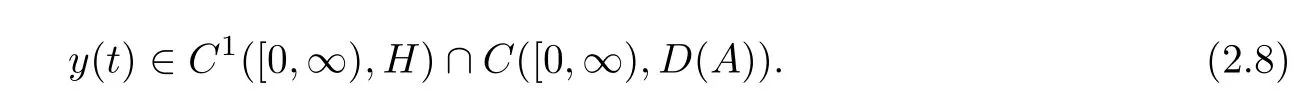
which can be expressed as

ProofSee,e.g.,Zheng[9].

Proof of Theorem 2.1ForU∈D(A),we compute

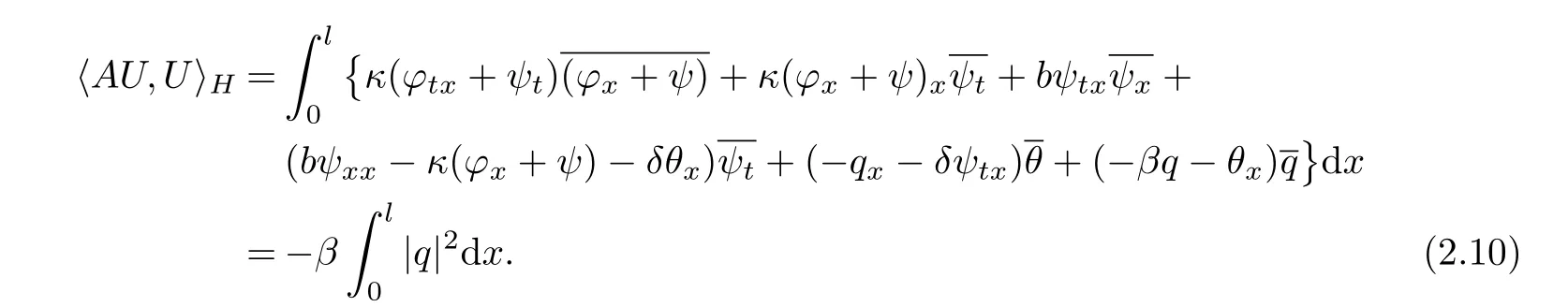
So,we obtainRe(AU,U)=−β‖q‖2≤0,which proves(i)in Lemma 2.1.

Moreover,we defineD(A)according to the Hilbert spaceHto make it dense inH.So condition(ii)in Lemma 2.1 is obviously holds.Applying Lemma 2.2,we complete the proof.

RemarkFor problem(2.1),we infer that:the energy functional is asymptotically stable only and only if

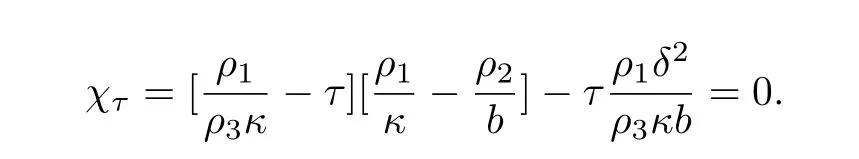
We can get the result by constructing several functionsF1(t),F2(t),F3(t),then set a Lyapunov functionL(t)=E(t)+N1F1(t)+N2F2(t)+N3F3(t),finally we need to prove

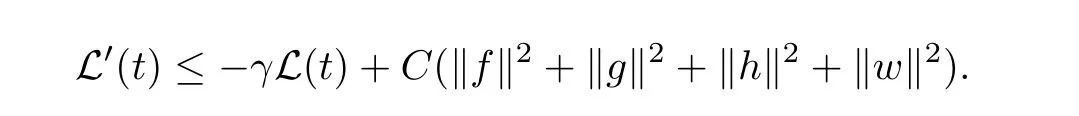
Then it follows

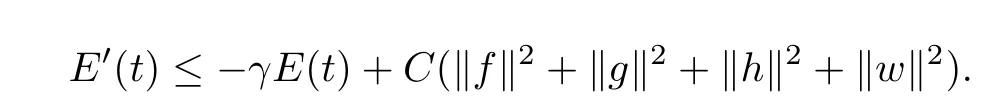
Using the theorem in reference Zheng[8]and Qin[6],we obtain the result.

§3.Global Existence of Semilinear Timoshenko System

In this section,we shall consider the following semilinear Timoshenko systems

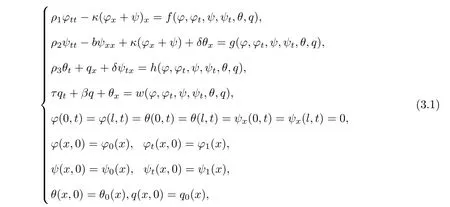
where(x,t)∈(0,l)×(0,+∞).Now we show the result.

Theorem 3.2We have the following results.

(1)Suppose thatf∈C1([0,∞),L2(J)),g∈C1([0,∞)(J)),h∈C1([0,∞),L2(J)),w∈C1([0,∞),L2(J))and▽f,▽g,▽h,▽ware uniformly bounded,then for anyU(0)=(ϕ0,0,ψ0,,θ0,q0)T∈H,problem(3.1)admits a unique mild global solution(ϕ(x,·),ψ(x,·),θ(x,·),q(x,·))such that(2)Furthermore,ifC1([0,∞),H1(J)),▽f,▽g,▽h,▽ware uniformly bounded andU(0)∈D(A),then problem(3.1)admits a unique classical solution(ϕ(x,·),ψ(x,·),θ(x,·),q(x,·))such that

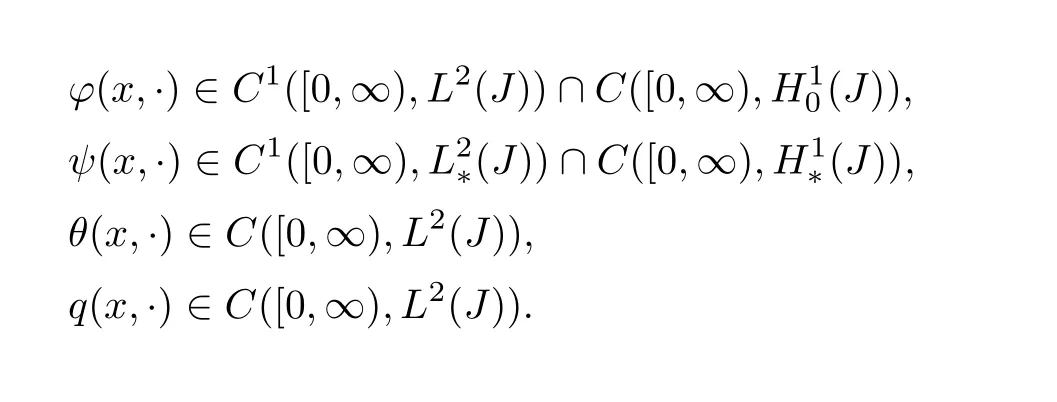
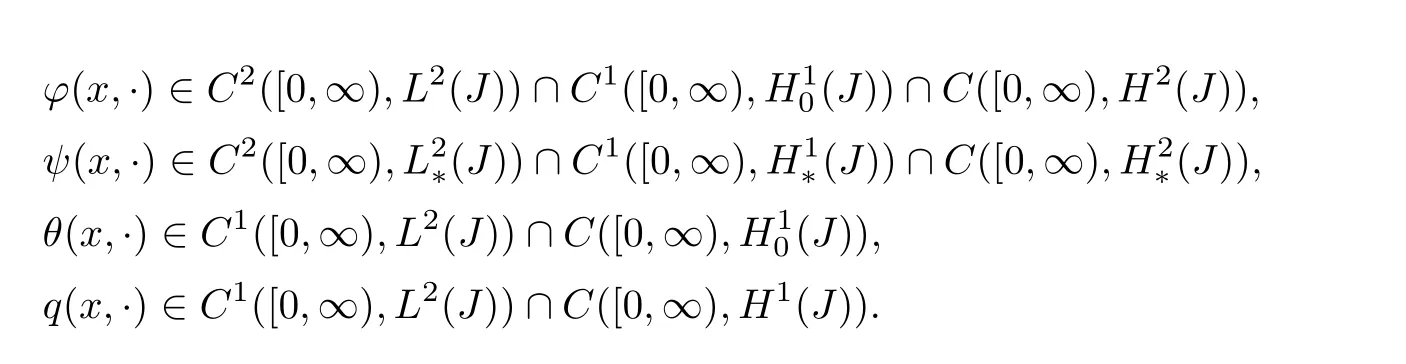
Theorem 3.3Suppose thatf∈C1([0,∞),L2(J)),g∈C1([0,∞)(J)),h∈C1([0,∞),L2(J)),w∈C1([0,∞),L2(J)).Then for anyU(0)=(ϕ0,,ψ0,,θ0,q0)T∈D(A),problem(3.1)admits a unique maximal solution(ϕ(x,·),ψ(x,·),θ(x,·),q(x,·))such that

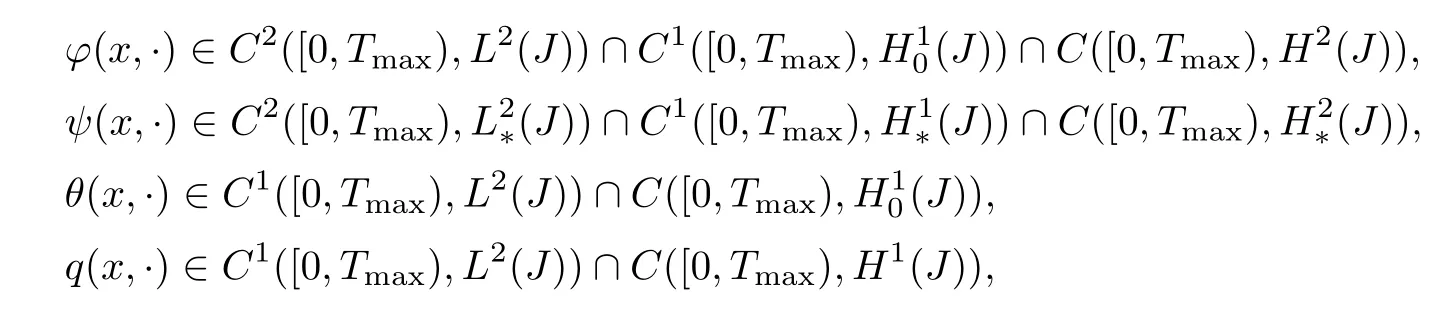
with

i.e.,the solution blows up in a finite timeTmax.

In order to obtain our results,we need some basic concepts from the book Zheng[9].For an abstract initial value problem

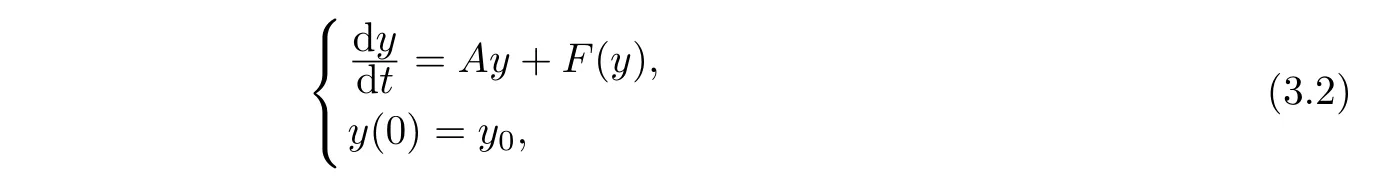
whereAis a maximal accretive operator defined in a dense subsetD(A)of a Banach spaceH,we have following lemmas.

Lemma 3.3Suppose thatFsatisfies the global Lipschitz condition,i.e.,there is a positive constant such that for ally1,y2∈H,

Furthermore,suppose thaty0∈H,then problem(7)admits a global mild solutiony(t)∈C([0,∞),H)and satisfies integral equation

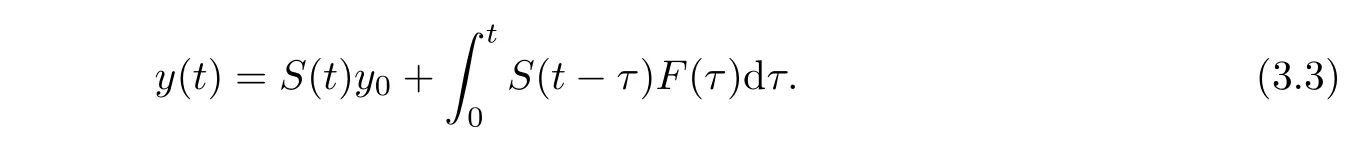
ProofSee,e.g.,Zheng[9].

Lemma 3.4Suppose thatF(y)is a nonlinear operator fromD(A)toD(A)and satisfies the global Lipschitz condition,i.e.,there is a positive constant such that for ally1,y2∈D(A),

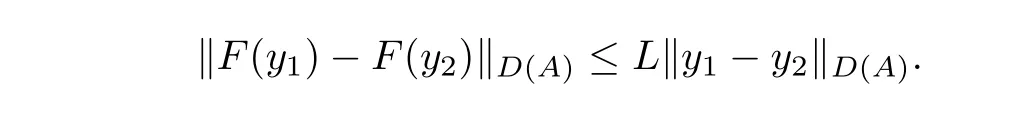
Then for anyy0∈D(A)problem(3.2)admits a unique classical solution.

ProofSee,e.g.,Zheng[9].

Lemma 3.5Assume thatAism-accretive andFis a nonlinear operator from a Banach spaceHtoHsatisfying the local Lipschitz condition.Then for anyy0∈H,there is a positive constantT＞0 depending on‖y0‖such that problem(3.2)in[0,T]admits a unique local mild solutiony∈C([0,T],H)such that

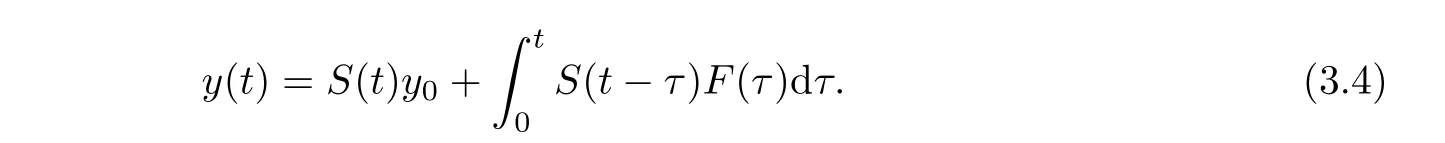
Furthermore,ify0∈D(A),thenyis Lipschitz continuous int∈[0,T].IfHis a reflexive Banach space,thenyis a classical solution.

ProofSee,e.g.,Zheng[9].

Lemma 3.6Under the same assumptions as Lemma 3.5,the solutionUcan be extended to a maximal mild solution in[0,Tmax),such that either

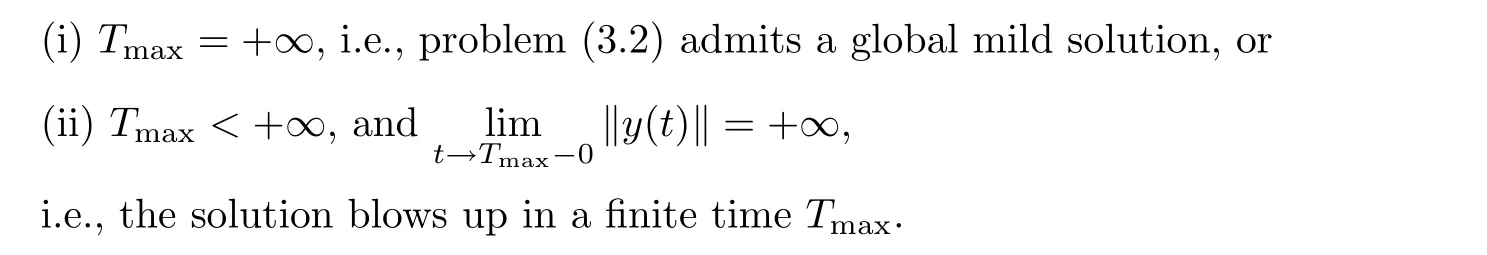
ProofSee,e.g.,Zheng[9].

Proof of Theorem 3.2Let

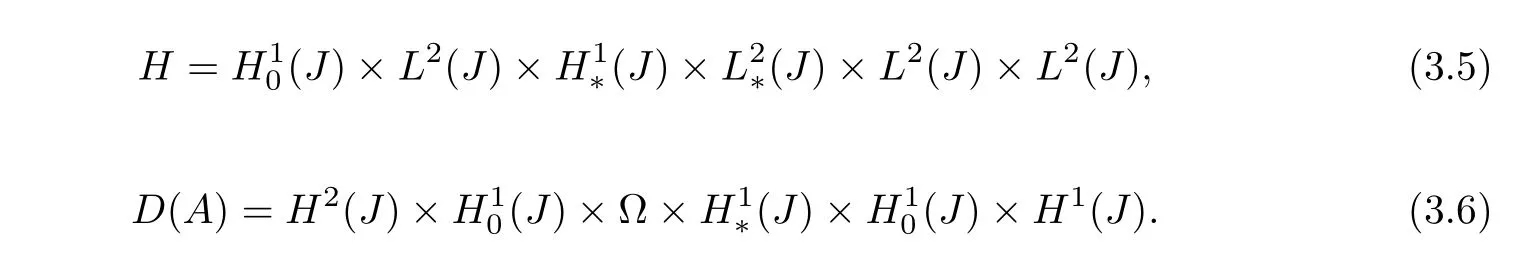
As proved before,we know thatAism-accretive.

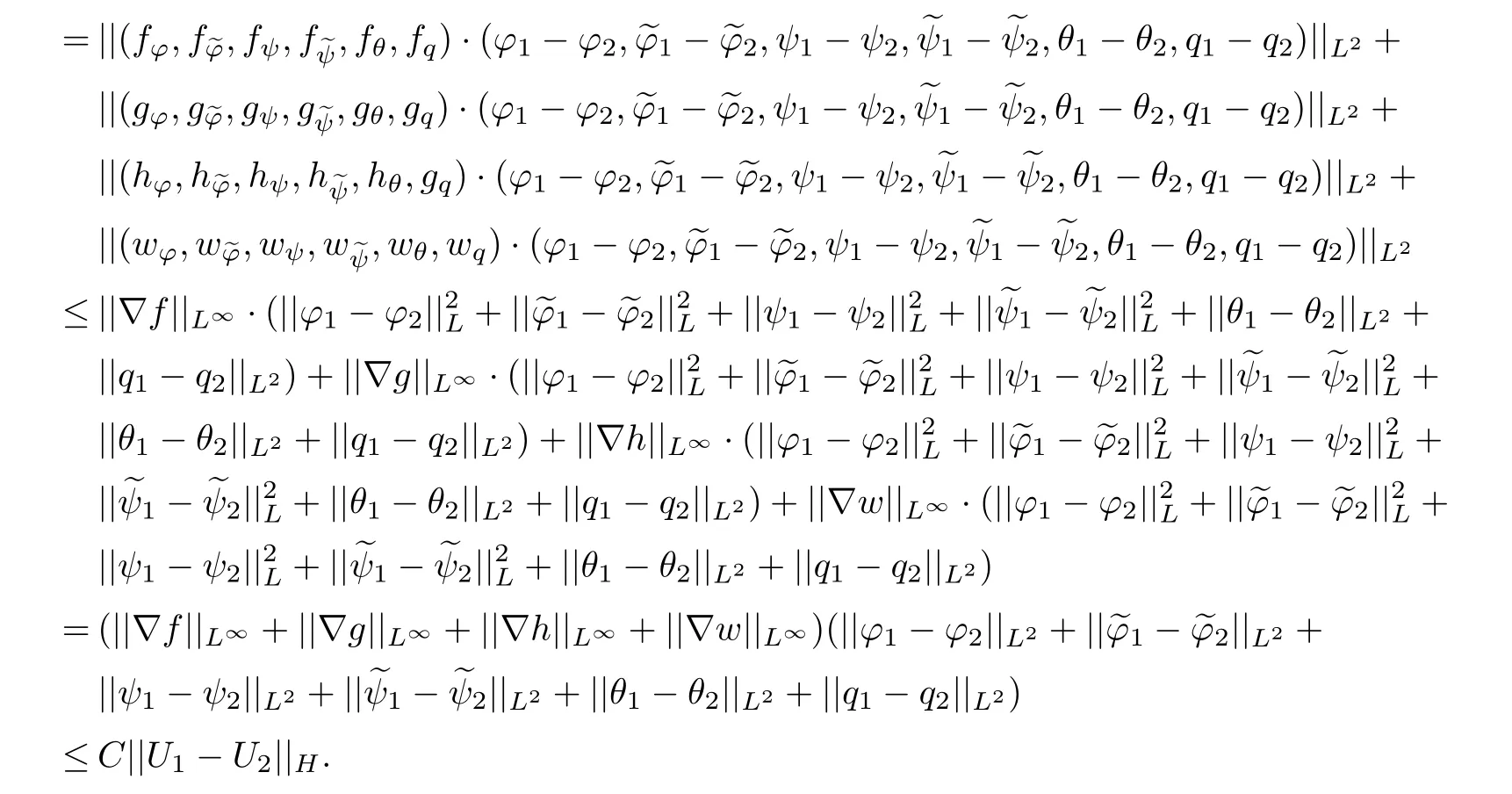
Therefore,Fsatisfies the global Lipschitz condition,by the assumption,Fis a nonlinear operator fromHintoH,F∈C1(H,H).

(2)Furthermore,for allU1=using the same method,we can obtain thatFsatisfies the global Lipschitz condition,by the assumption,andFis a nonlinear operator fromD(A)intoD(A),F∈C1(D(A),D(A)).Thus,from the book Zheng[9],we complete the proof.

Proof of Theorem 3.3Similar to the proof of Theorem 3.2,we haveH,D(A)andFis a nonlinear operator fromD(A)intoD(A),F∈C1(D(A),D(A)).Then we shall prove thatFsatisfies the local Lipschitz condition,in fact,for allU1=∈D(A),||U1||D(A)≤R,||U2||D(A)≤R,whereRis a positive constant.Then,we get

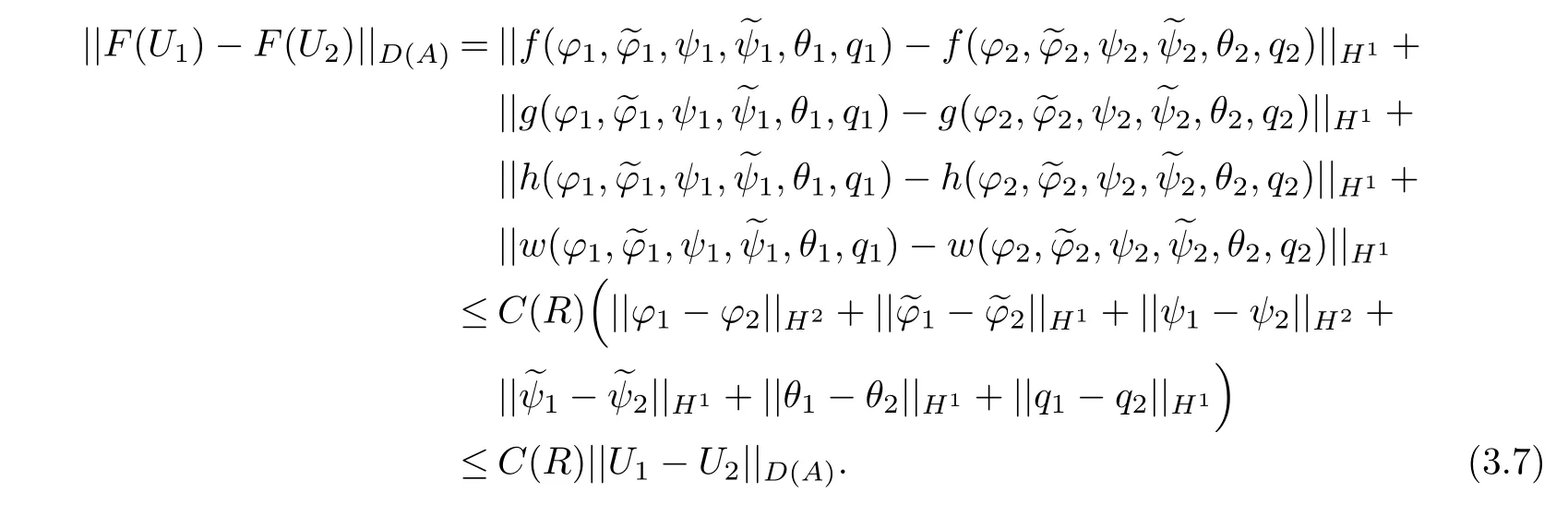
Thus,we use the theorems(2.5.4)and(2.5.5)in book Zheng[9]to complete the proof.

[1]ADAMS R A.Sobolev Spaces[M].Now York:Academic Press,1975.

[2]COLEMAN B D,GURTIN M E.Equipresence and constitutive equations for rigid heat conductors[J].Z Angew Math Phys,1976,18:199-208.

[3]DELL’ORO F,PATA V.On the stability of Timoshenko systems with Gurtin-Pipkin thermal law[J].J Differential Equations,2014,257:523-548.

[4]RIVERA MU˜NOZ J E,RACHE R.Mildly dissipative nonliear Timoshenko systems-global existence and exponential stability[J].J Math Appl Anal,2002,276:248-278.

[5]QIN Yu-ming,REN Jia,WEI Tian-hui.Global existence,asymptotic stability,and uniform attractors for non-autonomous thermoelastic systems with constant time delay[J].J Math Phys,2013,36(18):2540-2553.

[6]RACKE R,ZHENG Song-mu.Global existence and asymptotic behavior in nonlinear thermoviscoelasticity[J].J Differential Equations,1997,134:46-67.

[7]SANTOS M L,ALMEIDA J´UNIOR D S,MUN˜OZ RIVERA J E.The stability number of the Timoshenko system with second sound[J].J Differential Equations,2012,253:2715-2733.

[8]SARE FERN´ANDEZ H D,RACHE R.On the stability of damped Timoshenko systems:Cattane versus Fourier law[J].Arch Rational Mech Anal,2009,194:221-251.

[9]ZHENG Song-mu.Nonlinear Evolution Equations[M].USA:CRC Press,2004.