The Representation Problems of Conjugate Spaces of l0({Xi})Type F-normed Spaces

(Department of Mathematics,Changshu Institute of Technology,Changshu 215500,China)

§1.Introduction and Propositions

For a complicated and abstract mathematical objectA,if we can find a relatively simpler and more concrete objectBand an one-to-one mappingT:A→Bthat keeps the structures invariant,than the objectBor the mappingTis called a representation ofA.Representation theory is one of core problems for many branches of mathematics[1-4].For somel0typeF-normed scalar-valued sequence spaces,we obtained in[5]some representation theorems of their conjugate spaces.Extending scalar-valued sequence spaces to vector-valued sequence spaces,this paper study the representation problems of conjugate spaces of somel0({Xi})typeF-normed vector valued sequence spaces.

LetXbe a vector space over number field K(R or C).AnF-norm onXis a function‖·‖:X→R+with

If‖·‖is anF-norm,then it induces onXa meritable vector topology and(X,‖·‖)is called anF-normed space.If the monotonicity(n2)is replaced by the absolute homogeneity

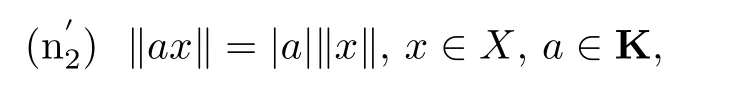
then‖·‖is called a norm and(X,‖·‖)a normed space.If condition(n2)is replaced by thep-absolute homogeneity(0＜p≤1)

then‖·‖is called ap-norm and(X,‖·‖)ap-normed space.

Let us make clear the meanings of other symbols used in the following.For a sequence(Xi,‖·‖i)of normed space,let

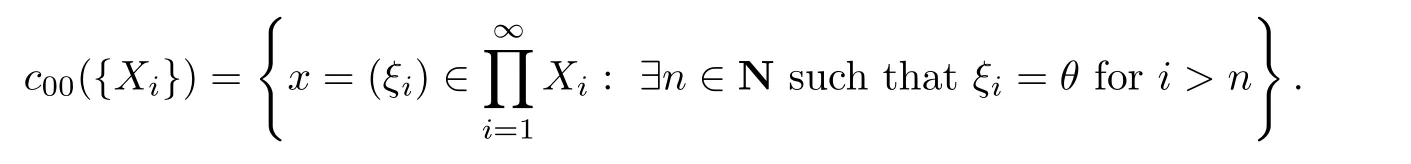
When(Xi,‖·‖i)≡(X,‖·‖),we usel0(X)to denotel0({Xi})and let

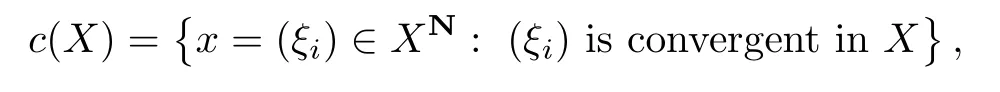
Now as vector spaces,we have natural inclusion relationsc00({Xi})⊂l0({Xi})and

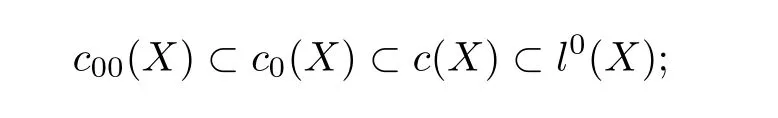
as topological vector spaces,the symbolsc00({Xi}),c00(X),c0(X)andc(X)are used to denote the corresponding normed spaces with the norm defined by

If()is used to denote the conjugate space of(Xi,‖·‖i)with the norm defined by

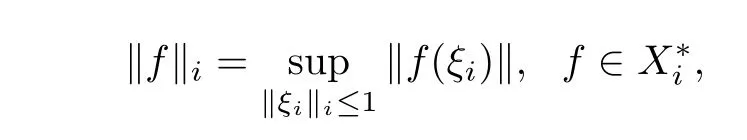
By the same arguments used in[6-7]it is easy to obtain

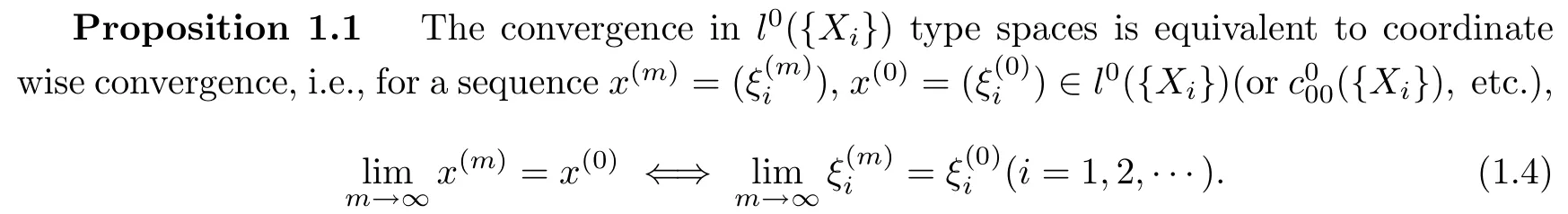
The following proposition reveals the intrinsic properties ofl0({Xi})type spaces,its proof is similar to that ofl0[5].

Proposition 1.2Everyl0({Xi})type spaces are all locally convex,but non-locally bounded.

For ap-normed space(X,‖·‖),if its conjugate spaceX∗is nontrivial,then the function

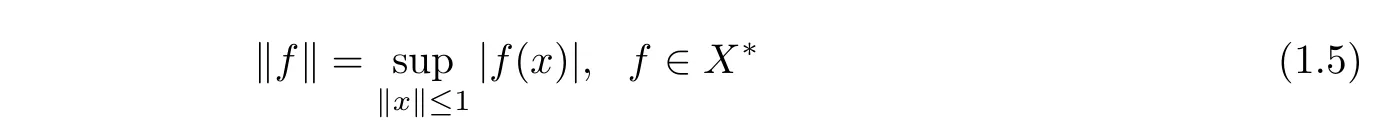
makes(X∗,‖·‖)into a new normed space.In this case,it is a very important subject to study the isometric representation of(X∗,‖·‖).Forl0({Xi})type spaces,the local convexity makes their conjugate spaces large enough to separate the points of them[6,8],but the non-local boundedness means that it is impossible to equip them with anyp-norm[7,P73].Thus it is also impossible to endow their conjugate spaces with anyF-norm via equation(1.5),so there is no sense in studying the isometric representation of their conjugate spaces.But now we can do the following two things

(a)Looking for the algebraic representation of their conjugate spaces;

(b)Looking for the topological representation of their conjugate space equipped with weak-star topologyw∗induced by the point wise convergence of nets

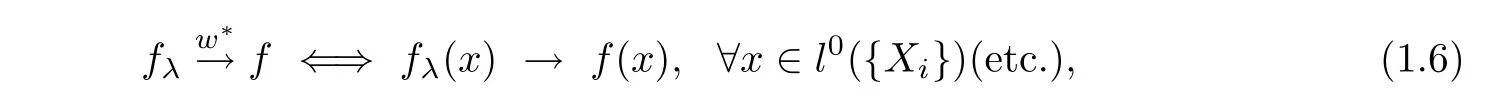
wherefλ,f∈¡l0({Xi})¢∗(etc.)(λ∈Λ).

In the next section,we study the algebraic representation problem of conjugate spaces ofl0({Xi})type spaces,obtain the algebraic representation continued equalities

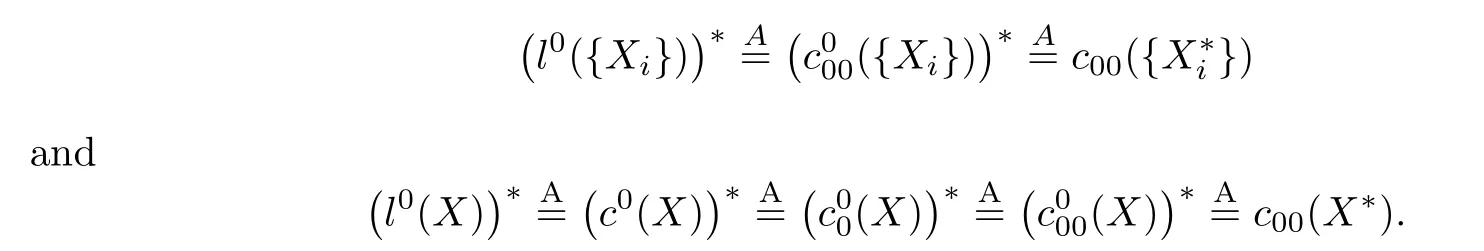
In the third section,with respect to the weak-star topologyw∗,we obtain the topological representationFor the sequence of inner product spaces and the number fields with the usual topology,the concrete forms of the basic representation theorems are obtained at last.

§2.The Algebraic Representation Theorems

Theorem 2.1Let(Xi,‖·‖i)be a sequence of normed spaces.Then the conjugate space(l0({Xi}))∗is algebraically isomorphic toc00(),i.e.,we have the algebraic representation

it could be represent as the series

Let

ProofThe continued equalities(2.7)is clearly equivalent to

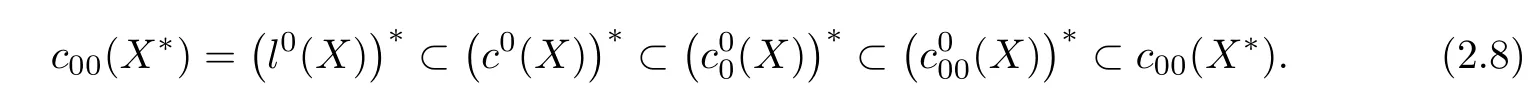
The equality on the left-hand side of(2.8)follows Theorem 2.1.IfE⊂Fandf∈F∗,then its restrictionf|E∈E∗and in this sense we haveF∗⊂E∗.Thus by natural inclusion relations

we have the three inclusion relations in the middle of(2.8).For anyf∈,we assert that the sequenceT(f)=(fi)=()∈c00(X∗),so we have the inclusion relation on the right end of(2.8).If not,there is an infinite subsequenceθ/=fij∈X∗.For eachfij,take aξij∈Xsuch thatfij(ξij)=1.Consider the sequence

which contradicts the continuity offon(X).This proves the relation ¡(X)¢∗⊂c00(X∗)and the continued equalities(2.7).

For a general sequence of normed spaces(Xi,‖·‖i),removing the corresponding objects¡c0({Xi})¢∗and ¡c00({Xi})¢∗(that may have no sense)from continued equalities(2.7),using the same arguments we can show

Theorem 2.3Let(Xi,‖·‖i)be a sequence of normed spaces.Then we have the algebraic representation continued equalities

§3.The Topological Representation Theorems

The following result will be used many times in the following.

Lemma 3.1LetX,Ybe two topological vector spaces andT:X→Ya linear mapping.SupposeXhas a countableθ-neighborhood basis,thenTis continuous if and only ifT(xn)→θinYfor every sequencexn→θinX.

ProofThe necessity is obvious,let us prove the sufficiency.IfTis discontinuous,then there exists aθ-neighborhoodV0inYsuch thatT−1V0is not aθ-neighborhood inX.Suppose{Un}is a countableθ-neighborhood basis inX.Take

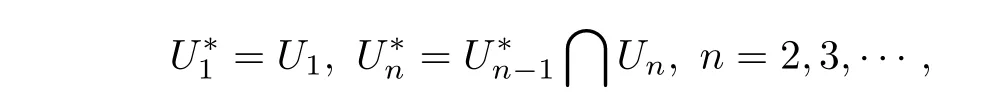
By the first part of(3.2)we havef/=θ;by the second part and the fact thatGis a subspace we knowf(x)=0,∀x∈G.Byf(xk)≡0,we havef∈Uandtf∈Ufor anyt＞0.Hence by(3.1)we have

so‖T(f)‖∞=0 andT(f)=θ.Thusf=θasTis an algebra isomorphism,the contradiction shows the discontinuity ofT.

Let us verify the discontinuity ofT−1now.For each natural numberi,take anfi∈with‖fi‖i=1.Then the sequence

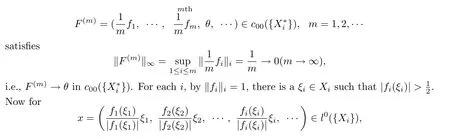
by equality(2.6),we have

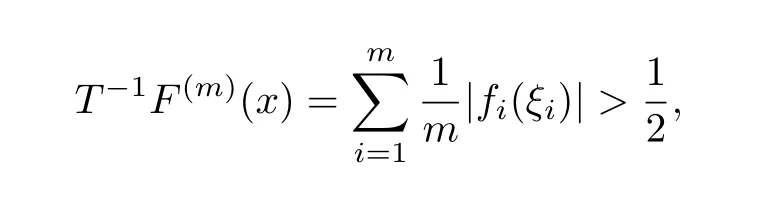
i.e.,T−1F(m)w∗/→θ(m→∞).This proves the discontinuity ofT−1.

Theorem 3.2Let(Xi,‖·‖i)be a sequence of finite dimensional normed spaces.Then the mapping

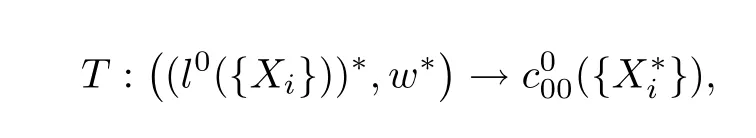
defined by(2.5)is continuous,but its inverseT−1is not,wherec000()is theF-normed space with theF-norm‖·‖0.

ProofBecause the identity mappingI:orem 3.1,we know that the inverseT−1from

Let us verify the continuity ofTnow.If not,then there is a net{f(λ):λ∈Λ}⊂¡l0({Xi})¢∗that converges in weak-star topology toθ,but its imagine

does not convergeθin

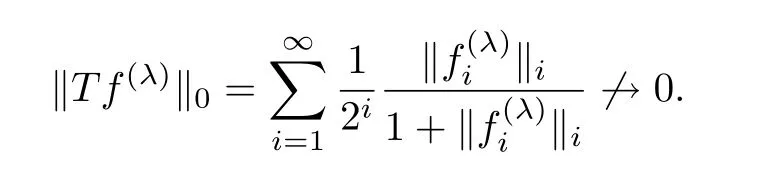
ProofReplacing the spacel0({Xi})by({Xi}),using the same argument in the proof of Theorem 3.1,we can verify the discontinuity ofTnow.To prove the continuity of the inverseT−1,suppose a sequence

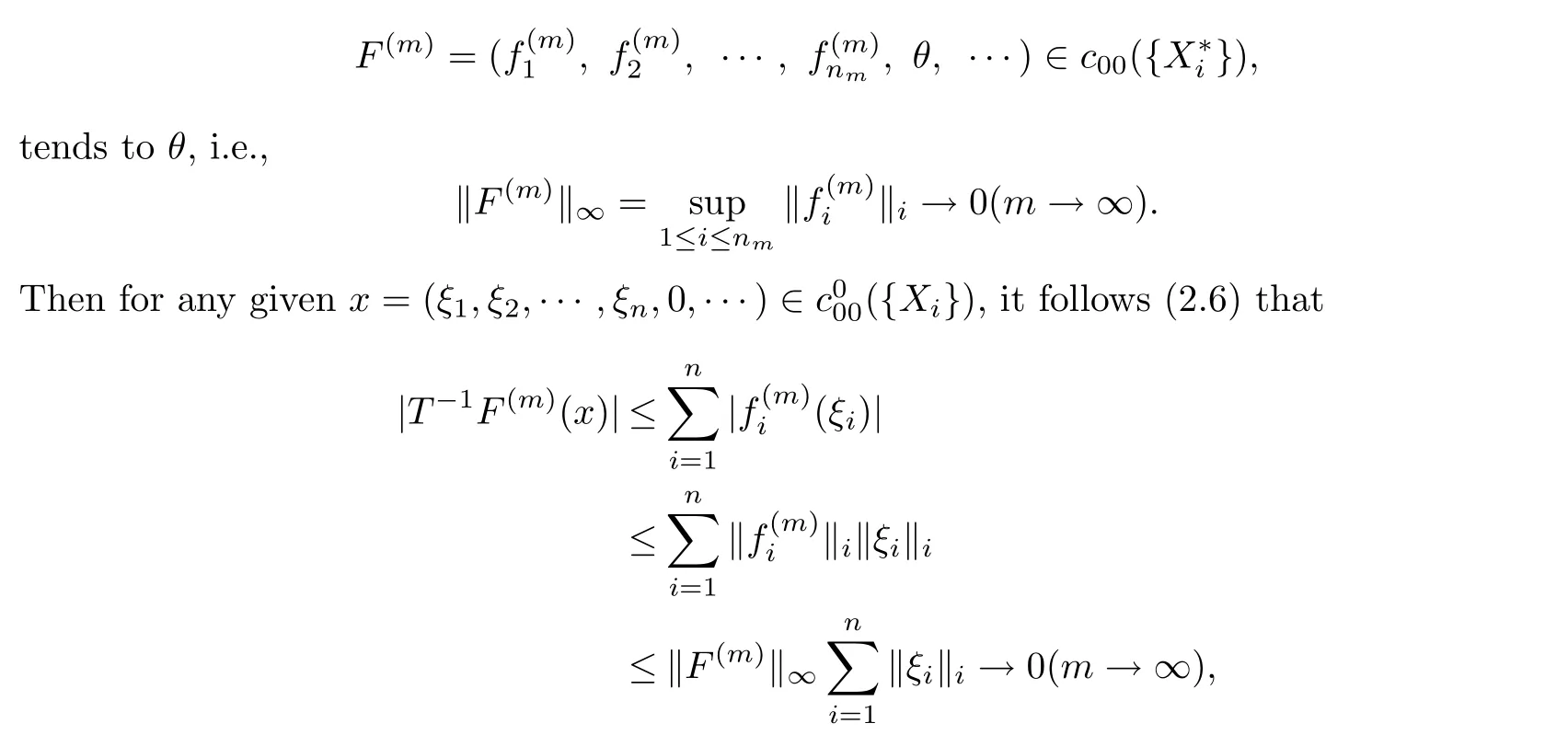
i.e.,T−1F(m)converges in weak-star topology toθinThis completes the proof of continuity of the inverseT−1by Lemma 3.1.

Theorem 3.4Let(Xi,‖·‖i)be a sequence of finite dimensional normed spaces.Then the mapping

defined by(2.5)and its inverseT−1are all continuous or we have the topological representation

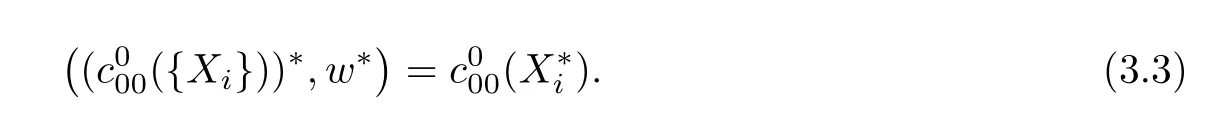
ProofReplacing the spacel0({Xi})by({Xi}),by the same argument used in the second part of proof of Theorem 3.2,we can verify the continuity ofTnow.To prove the continuity of the inverseT−1,suppose a sequence

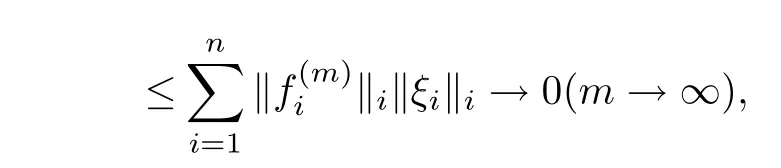
i.e.,T−1F(m)converges in weak-star topology toθinof continuity of the inverseT−1and the topological representation(3.3).

By the above four theorems we can obtain the following results immediately

Corollary 3.1Let(X,‖·‖)be a finite dimensional normed space.

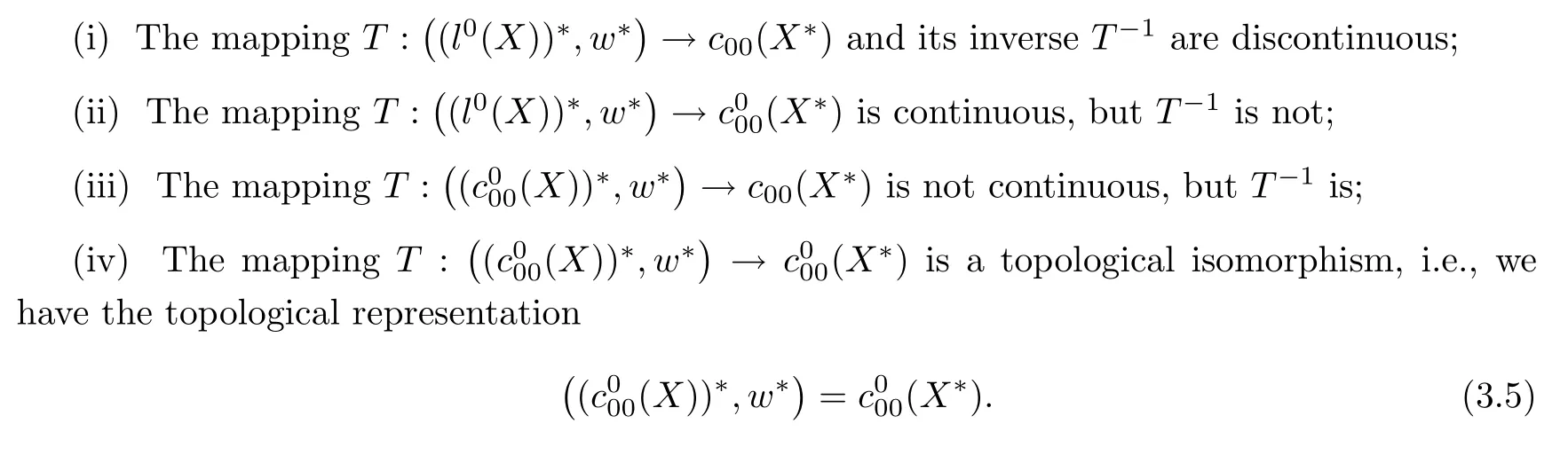
§4.The Concrete Forms of the Basic Representation Theorems

Inner product spaces and the number fields with the usual topology are two typical classes of normed spaces.For these two classes of normed spaces,let us find the concrete forms of the basic representation theorems obtained in previous sections.

Theorem 4.1(i)Let(Xi,〈·,·〉i)be a sequence of inner product space.Then we have the algebraic representation continued equalities

ProofBy the self-conjugate propertyX∗=Xof inner product spaces and the general form of continuous linear functionals on them[11,P104],the conclusion(i)follows Theorem 2.1 and Theorem 2.3,(ii)follows Theorem 2.2,(iii)follows Theorem 3.4.

Theorem 4.2(i)In the sense of isomorphism,we have the algebraic representation continued equalities

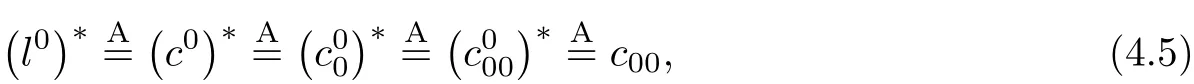
i.e.,anyf∈¡l0¢∗(orf∈¡c0¢∗,etc.)corresponds to a unique

such that

(ii)In the sense of isomorphism,we have the topological representation

ProofThe number field K with the usual topology is just an inner product space under the multiplication〈ξ,ζ〉=ξ·ζ,so by the latter two conclusions of Theorem 4.1,we get the corresponding results of this Theorem.

AcknowledgementThe author is grateful to Professor LUO Xian-fa for his helpful suggestions.

[1]JARCHOW H.Locally Convex Spaces[M].Stuttgart:B G Teubner,1981.

[2]WANG Guo-jun.Stone’s Representation Theorem and Generalized Space Theory[J].Journal of Jianghan Petroleum Institute,1996,18(3):122-128(in Chinese).

[3]WANG Jian-yong.The subrepresentation theorem of the conjugate cone of locallyβ-convex spaceLβ(µ,X)(0＜β≤1)[J].Acta Mathematica Sinica,2012,55(6):961-974(in Chinese).

[4]WANG Jian-yong.The presentation problem of the conjugate cone of hardy spaceHp(0＜p≤1)[J].Chinese Ann Math,2013,34B(4):541-556.

[5]WANG Jian-yong.The representation theorems of the Conjugate spaces of somel0typeF-normed spaces[J].Acta Mathematica Sinica,2016,59(4):519-526(in Chinese).

[6]ROLEWICZ S.Metric Vector Spaces[M].Warszawa:PWN-Polish Scientific Publishers,1985.

[7]WANG Jian-yong.An Introduction to Locallyp-Convex Spaces[M].Beijing:Science Press,2013(in Chinese).

[8]KALTON NJ,PECK NT,ROBERTS JW.AnF-space Sampler[M].London:Cambridge University Press,1984.

[9]KELLY JL.General Topology[M].New York:Van Nostrand,1955.

[10]MEGGINSON RE.An Introduction to Banach Space Theory[M].New York:Springer-Verlag,1998.

[11]LANG S.Real and Functional Analysis(3nd ed)[M].New York:Springer-Verlag,1993.