裂隙岩样端面的分形维数计算
王兴宏
(中煤科工集团重庆设计研究院有限公司, 重庆 400042)
裂隙岩样端面的分形维数计算
王兴宏
(中煤科工集团重庆设计研究院有限公司, 重庆 400042)
为了定量描述试样端面裂隙的发育程度,基于网格盒子法,计算得出了试样端面裂隙的分形维数,并使用MTS815岩石多功能试验机测试裂隙岩样的渗透系数,通过试样的分形维数及试验测试结果对比发现:试样裂隙越发育,计算出的分形维数越大,且通过试验测试的渗透系数也越大;同时,试样受荷载循环加载次数的增大,分形维数对试样的渗透系数影响越小。
裂隙岩体;分形维数;渗透系数
0 引 言
分形几何学是Mandelbrot在20世纪70年提出来的,随着分形理论的发展,特别是在自然科学中有着广泛的应用。目前,国内很多学者对分形理论在岩石力学及流体力学中的应用进行了研究,谢和平[1]讲述了分形几何学在岩土力学中的应用;张彦洪[2]从渗流的角度出发,对岩体裂隙网络运用分形理论分析,提出了计算岩体结构面信息维数的计算方法,并建立了信息维数与渗透系数的关系;冯增朝[3]基于岩体裂隙的分形规律,研究了其单轴抗压强度与分形维数的关系;陈尚星[4]以土裂隙的分布规律为研究基础,得出分形维数是评价裂隙发育程度的综合指标;王维华[5]基于分形理论定量裂隙演化规律,建立了裂隙变化量化参数之间的关系;李宏艳[6]基于分形理论定量描述采动影响区覆岩裂隙时空演化规律;张永波[7]利用相似材料模拟采动岩体裂隙,同时采用分形几何理论来研究采空区岩体裂隙分布的分形规律。
岩土工程中的岩体存在大量的裂隙,有的发育短,有的发育长,这些通过肉眼可以明显辨别出来,但没法对其进行定量,因此,本文采用分形理论对岩体裂隙的发育程度进行定量描述,通过对标准裂隙岩样进行渗透试验,计算出裂隙岩样的渗透系数,揭示了裂隙岩样的分形维数与渗透系数的关系。
1 岩样分形维数的计算方法
本次试样尺寸为Φ50 mm×100 mm,为了符合本次实验的研究要求,选取了3个裂隙比较发育的试件,本实验在MTS815岩石多功能试验机上进行,对岩样M01、M02、M03进行轴压为6,8 MPa下不同围压的渗透系数测试。
网格盒子法适用于对岩体断裂、地质断层等此类分形特征的计算,是把同等尺寸的正方形小网格作为覆盖分形体的盒子。如图1所示,从小到大变化,当δi分别为1,2,3,4,5,6,7,8,9,10时,对应尺寸δi计算出覆盖裂隙的盒子数目N(δi),对(logδi-1, log(N(δi)))数组的散点图,使用最小二乘法进行直线拟合,求出该直线的斜率,即为所计算分形体的分形维数。
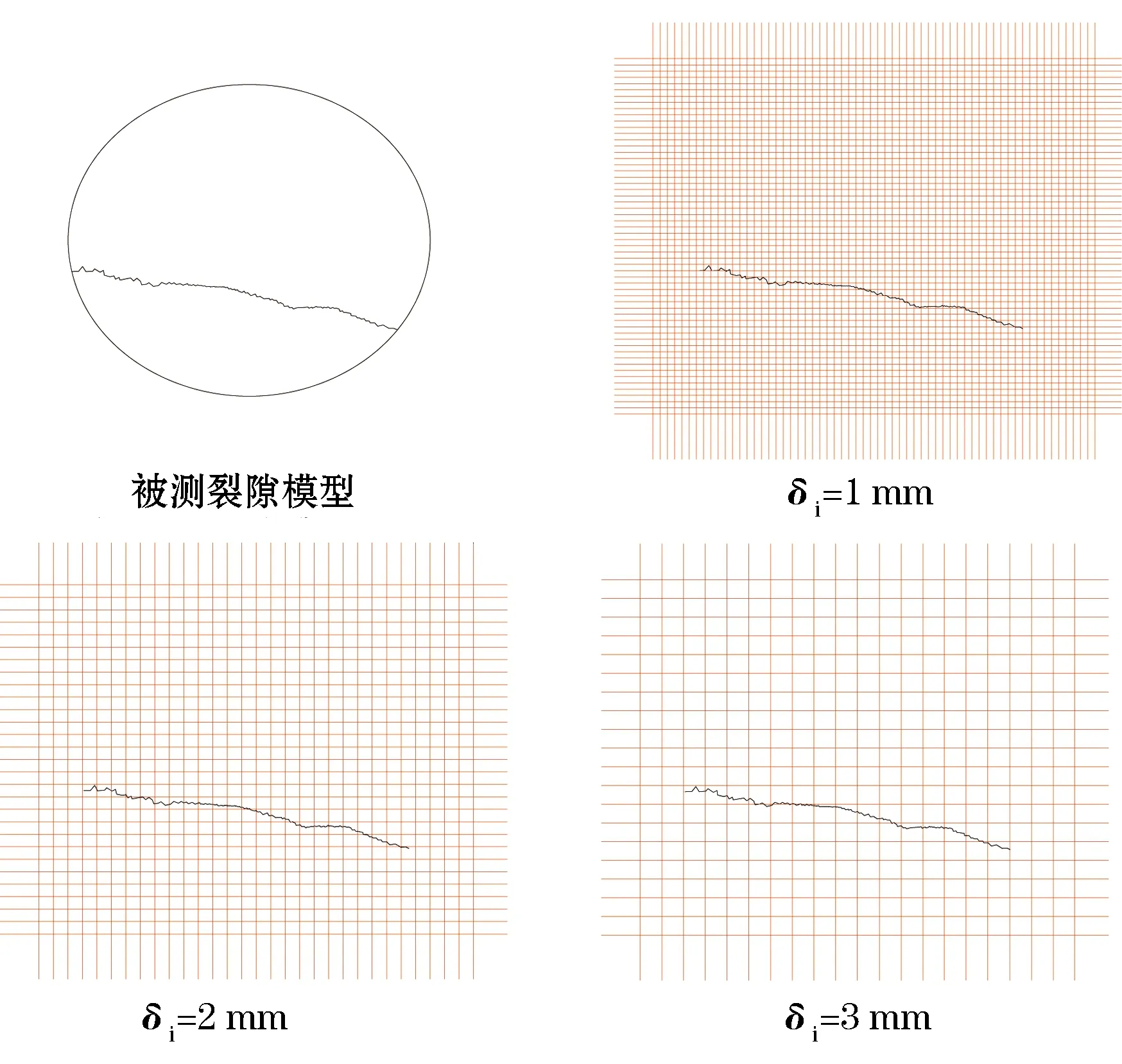
图1 不同测量尺度测量被测裂隙模型
2 岩样分形维数的计算及其结果
本次分形维数的计算对象为岩样端面裂隙,由于其为二维裂隙平面,故用网格盒子法进行计算。采用AutoCAD对岩样端面按等尺寸大小进行素描(见图2),以岩样M02为例,按以下步骤进行计算。

图2 被测裂隙模型
(1) 确定分形所用盒子边长尺寸,即测量尺度δi。测量尺度δi分别取1,2,3,4,5,6,7,8,9,10 mm。
(2) 分别计算出测量尺度δi分别为1,2,3,4,5,6,7,8,9,10 mm覆盖下的裂隙盒子数目N(δi),不同测量尺度下的覆盖盒子数目见表1。
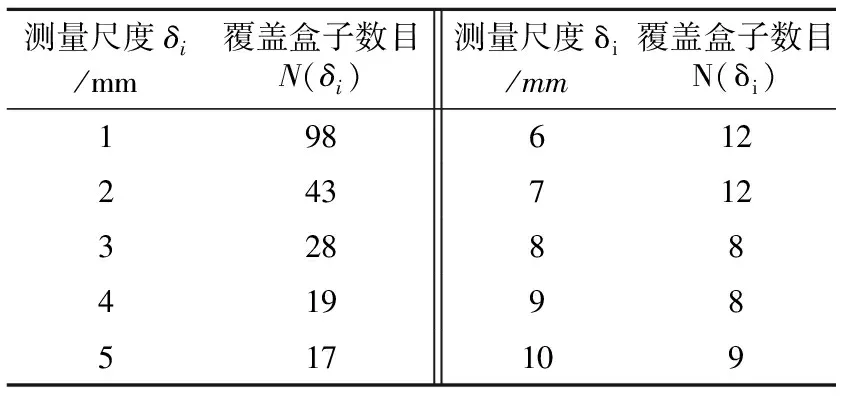
表1 不同测量尺度下覆盖盒子数目
(3) 对数据组(logδi-1, log(N(δi)))(i=1,2,3,4,5,6,7,8,9,10)进行最小二乘拟合。其计算公式见式(1)。
(1)
式中,n为10;α、β为拟合参数。
(4) 拟合曲线的斜率β为覆盖体所测分形维数。通过计算,岩样M02(上)端面裂隙的分形维数为1.10087,其拟合曲线相关系数0.98229,表明拟合曲线具有较高的拟合度,能很好地反映数据点分布规律。表2为不同岩样端面分形维数。
由表3可知,对比岩样M02(上)与M02(下),前者裂隙发育程度明显较后者高,计算出的分形维数也可得到验证,当裂隙发育程度对比相差不明显时,通过计算分形维数可以得出相关结果,同理对比分析岩样M07和M12,亦可得到相同的分析结果。
3 岩样分形维数与渗透系数的关系
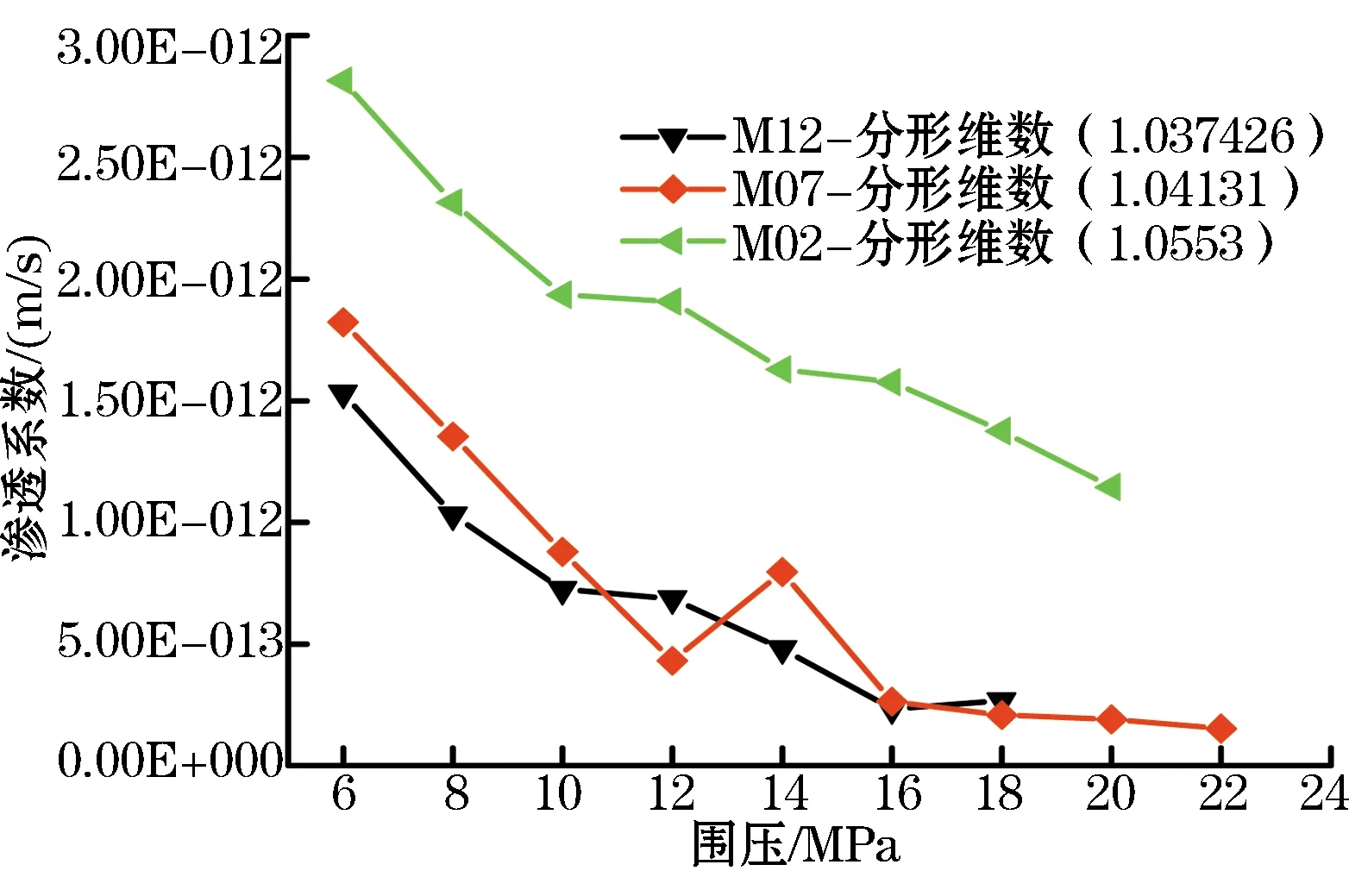
由图3可知,对试样施加轴压6 MPa,随围压增大,渗透系数不断减少;通过岩样M02、M07、M012三者渗透系数的对比,可明显判别出三者之间的渗透系数关系:M02 表3 不同岩样端面的裂隙分布情况 图3 轴压6 MPa作用下的渗透系数-围压曲线 由图4可知,对试样施加轴压8 MPa,随围压的增大,渗透系数不断减少;通过岩样M02、M07、M12三者渗透系数的对比,可知三者渗透系数大小相差不大,且几乎不受岩样裂隙分形维数大小的影响,即裂隙的发育程度;根据裂隙闭合机制[8],随试样受荷载循环加载次数增加,裂隙张开度减少,且会逐渐趋于稳定值,且该值很小,因而三者之间的渗透系数很小且比较接近。 由以上可知,当岩样隙宽相等时,裂隙分形维数较大的渗透系数也较大,当裂隙隙宽基本相等时,分形维数基本可以作为衡量岩石渗透系数相对大小的指标。 岩土工程中岩体存在大量的裂隙,为了定量描述试样端面裂隙的发育程度,本文基于网格盒子法,得出了试样端面裂隙的分形维数,并使用MTS815岩石多功能试验机测试裂隙岩样的渗透系数,试样的分形维数及试验测试结果表明,试样裂隙越发育,计算出的分形维数越大,且通过试验测试的渗透系数也越大;同时,试样受荷载循环加载次数的增大,分形维数对试样的渗透系数影响越小。 [1]谢和平.分形几何及其在岩土力学中的应用[J].岩土工程学报,1992(01):14-24. [2]张彦洪,柴军瑞.考虑渗流特性的岩体结构面分形特性研究[J].岩石力学与工程学报,2009,28(S2):3423-3429. [3]冯增朝,赵阳升.岩体裂隙分维数与岩体强度的相关性研究[J].岩石力学与工程学报,2003(S1):2180-2182. [4]陈尚星.基于分形理论的土体裂隙网络研究[D].南京:河海大学,2006. [5]王维华.基于分形理论的采动覆岩裂隙渗透规律研究[J].煤炭技术,2015,34(09):208-211. [6]李宏艳,王维华,齐庆新,等.基于分形理论的采动裂隙时空演化规律研究[J].煤炭学报,2014(06):1023-1030. [7]栗东平,周宏伟,薛东杰,等.煤岩体采动裂隙网络的逾渗与分形特征关系研究[J].岩土力学,2015(04):1135-1140. [8]郭保华,李小军,苏承东.岩石裂隙法向循环加载本构关系试验研究[J].岩石力学与工程学报,2012(S1):2973-2980.(收稿日期:2016-10-12)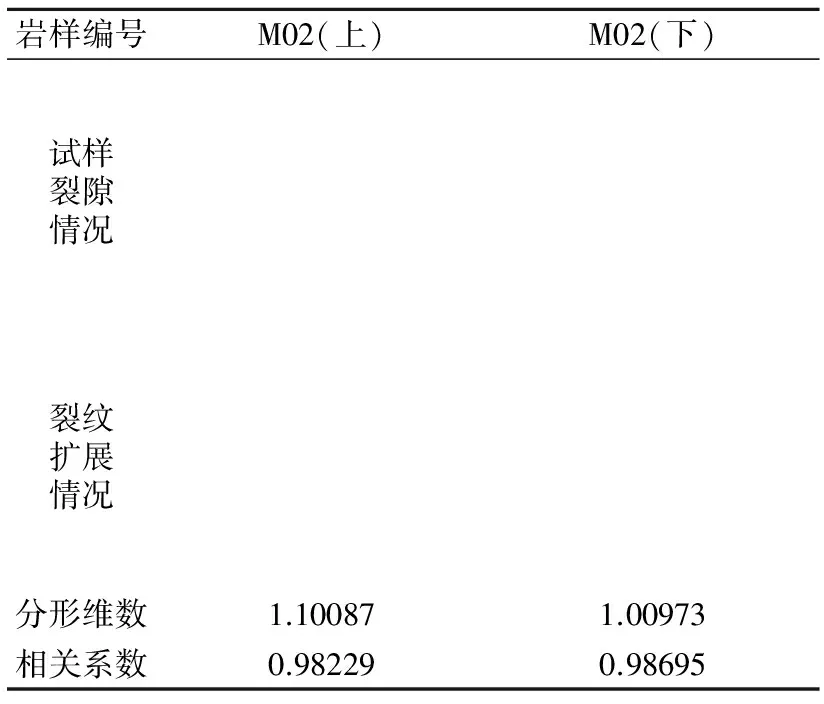
4 结 论

