船舶电力推进永磁同步电机SVM-DTC控制系统优化
李云鹏,赵宏革,李世霖,孙军浩,冯 杨
(大连海事大学 轮机工程学院,辽宁 大连 116000)
船舶电力推进永磁同步电机SVM-DTC控制系统优化
李云鹏,赵宏革,李世霖,孙军浩,冯 杨
(大连海事大学 轮机工程学院,辽宁 大连 116000)
针对船舶电力推进永磁同步电机(PMSM)直接转矩控制系统存在较大转矩脉动问题,论文提出了一种基于双PI的空间矢量调制(SVM-DTC)直接转矩控制新策略。该控制策略通过空间矢量调制合成电压矢量,代替传统开关表与滞环比较器,采用两个PI调节器分别对电压矢量角度与幅值进行控制,在保持系统结构简单的基础上,显著地减小转矩脉动,具有较强的鲁棒性,改善了船舶电力推进系统中永磁同步电机的稳态性能与动态性能,优化效果明显。仿真结果证实了该控制策略的有效性。
船舶电力推进 直接转矩控制 空间矢量调制 PI调节器 转矩脉动
0 引言
直接转矩控制(Direct Torque Control,简称DTC)是 20世纪 80年代 Takahashi、Noguchi和Depenbrock[1, 2]提出的高性能交流电机控制策略,采用定子磁链定向和空间矢量概念,通过检测定子电压、电流、直接在定子坐标系下观测电机的磁链、转矩、并将此观测值与给定磁链、转矩相比较差值经滞环控制器得到应控制信号,再综合当前磁链状态来选择相应电压空间矢量,实施直接对电机转矩的控制。由于拥有结构简单、动态响应快、对电机参数鲁棒性强等优点,DTC在交流电机传动领域流行起来。但由于直接转矩控制技术采用定子磁链幅值和转矩的bang-bang控制,必然导致电机在运行中存在转矩脉动,尤其在大容量大转动惯量系统中运行时,转矩脉动更为明显,这限制了直接转矩控制在船舶电力推进系统中的运用[3]。对此,国内外学者提出了许多改进方法,例如:文献[4]、[5]通过从开关表中获取有效电压矢量的占空比来改变电压矢量长度,该策略能够显著减小转矩脉动,但获取占空比的计算过于复杂且高度依赖电机参数,失去了传统直接转矩控制鲁棒性强的优点。文献[6]、[7]各自提出了基于空间矢量调制直接转矩控制的不同策略,其理论上能产生无限个连续的电压矢量,有效减小转矩脉动,控制结构与矢量控制相似,但以上策略在通过空间矢量调制技术合成期望的电压矢量之前需要进行旋转坐标变换,这大大增加了系统的复杂程度。文献[8]、[9]在三电平逆变器的基础上改用五级滞环比较器,构造更为精细的开关表,在一定程度上减小了转矩脉动,但其开关表过于复杂。文献[10]、[11]引入模糊控制的方法,对磁链的空间位置、转矩和磁链差值进行模糊分级,优化电压矢量的选择,但该策略在大容量、大转动惯量系统中转矩脉动优化效果不佳。为此,本文提出了一种新策略,对船舶电力推进永磁同步电机直接转矩控制系统进行优化分析。
1 传统DTC电压矢量选择策略
如图1所示,在传统直接转矩控制中,如果定子磁链矢量位于某个区域内,几个固定的电压矢量(V1,V2,V3,V4,V5,V6,V7(V0))中的一个会被选择,这取决于磁链与转矩滞环比较器的输出。由于电压矢量有限,传统直接转矩控制策略并不能精确地调节转矩与磁链,由此带来转矩脉动过大的负面效果。
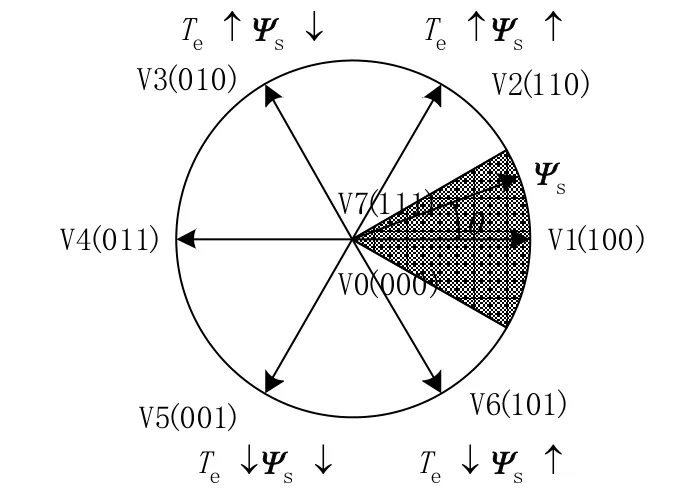
图1 传统直接转矩控制电压矢量选择方案
2 SVM-DTC电压矢量选择策略
相对于传统的直接转矩控制只能选择有限个不连续的电压空间矢量,基于空间矢量调制的直接转矩控制(SVM-DTC)可以合成任意个电压空间矢量,实现电压矢量平稳切换,有效减小磁链和转矩脉动[12]。
参考电压与磁链位置关系如图2所示,其中Ψs、Ψr分别为定子和转子磁链;Ψsref为定子磁链的参考值,在直接转矩控制系统中为定子磁链给定值;δ为定子磁链与转子磁链夹角,即转矩角;θs、θr分别为定子磁链和转子磁链与 α轴夹角;ΔΨ、Δδ分别为参考电压作用ΔT时间后的定子磁链的增量和转矩角的增量;usref为参考电压。空间电压矢量调制模块利用计算出的参考电压值,判断出参考电压矢量所在扇区,由参考电压所在扇区相邻的两个有效电压空间矢量和零电压矢量合成新的电压空间矢量,替换传统直接转矩控制中的电压矢量开关表。图3所示为SVM-DTC系统框图。
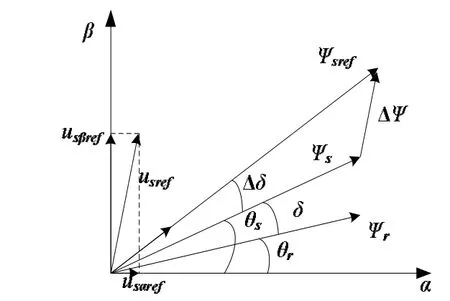
图2 参考电压与磁链的空间位置关系
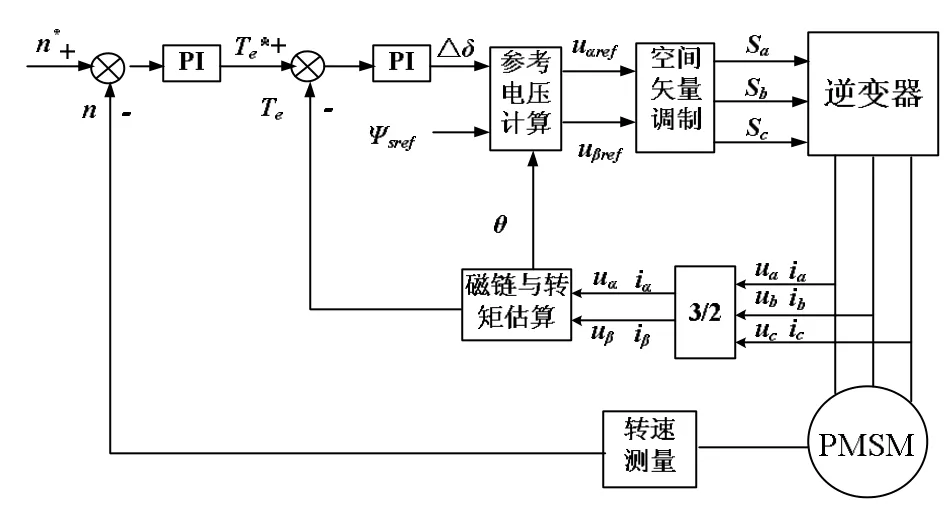
图3 SVM-DTC系统结构图
3 双PI SVM-DTC优化控制策略
在SVM-DTC系统基础上,本文提出了一种改进策略,双PI SVM-DTC系统框图如图4所示,系统主要由转速PI调节器、电压矢量角度PI调节器、电压矢量幅值PI调节器、磁链和转矩估算、参考电压计算、空间电压矢量调制和逆变器模块构成。电机的电磁转矩、定子磁链值和角度通过磁链和转矩的计算模块计算出;由转速PI调节器得出电机的给定转矩Te*,转矩PI调节器计算出电机负载角的增量 Δδ,并通过电压矢量角度 PI调节器生成φ、电压矢量幅值PI调节器生成m;然后经过空间电压矢量调制模块的出对应的逆变器开关信号,控制电机运行。
3.1 电压矢量角度确定
假设定子磁链角已知,在图5所示位置。若要磁链和转矩同时增大,应选择位于区域 [Ⅰθ +10°,θ +80°]范围内的候选电压矢量。为了避免磁链或转矩的突然变化,[θ,θ +10°)和(θ +80°,θ +90°]范围内的区域不被考虑[13]。当转矩误差大时,应选择θ +80°附近的电压矢量;当转矩误差小时,应选择θ +10°附近的电压矢量。若要磁链减小,转矩增加,则应选择区域 Ⅱ[θ +100°,θ+170°]范围内的候选电压矢量。当转矩误差大时,应选择θ +100°附近的电压矢量;当转矩误差小时,应选择θ +170°附近的电压矢量。位于Ⅲ,Ⅳ区域候选电压矢量的选择以此类推。由此,相对于定子磁链位置的电压矢量角度增量可表示为:
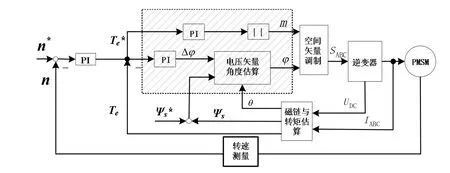
图4 双PI SVM-DTC系统结构图
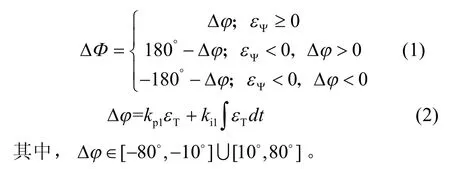
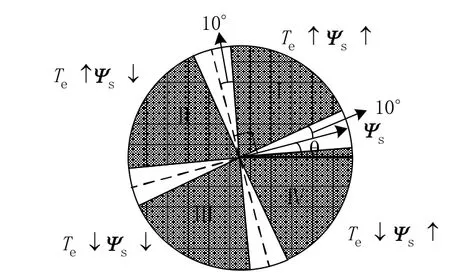
图5双PI SVM-DTC电压矢量选择方案
这里kp1ki1、εT、εΨ和Δφ分别表示比例系数、积分系数、转矩误差、定子磁链误差和电压矢量角度PI调节器输出值。对Δφ限幅后应使其满足|Δφ|[10°∈ ,80°]。电机刚启动时,为了加快建立定子磁链,在定子磁链首次不小于给定磁链之前,重新 Δφ对进行限幅,满足|Δφ|[10°∈ ,60°];待定子磁链建立完成后恢复|Δφ|[10°∈ ,80°]。
最终,电压矢量角度可表示成:

3.2 电压矢量幅值确定
电压矢量角度与幅值都能够对转矩产生影响,本文采用电压矢量幅值PI调节器来调节电压矢量幅值,计算中为了确保电压矢量为非负值,对电压矢量幅值PI调节器的输出结果加绝对值,即
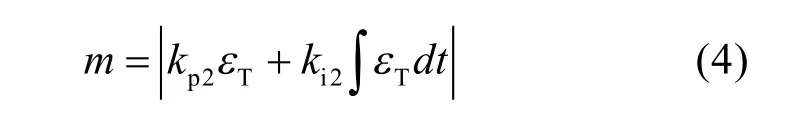
在分别获取了电压矢量角度与幅值后,极坐标下电压矢量最终表示为:

3.3 转矩与定子磁链估算
在直接转矩控制系统中,转矩脉动与定子磁链脉动是衡量直接转矩控制策略性能优劣的两个主要指标,在应用于船舶电力推进直接转矩控制系统中转矩脉动显得尤为重要,本文采用 u-i模型估算电机的定子磁链值,其在α-β坐标系下可表示为:
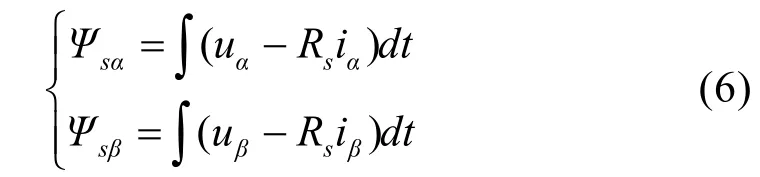
这里iα,iβ,uα,uβ分别为定子电流和定子电压在α、β轴上的分量;Rs为定子电阻;Ψsα,Ψsβ分别为定子磁链在α、β轴上的分量。
两相静止坐标系下,永磁同步电机的转矩方程为:
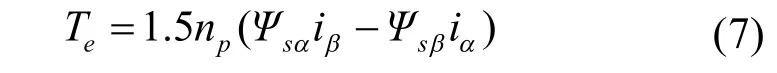
上式中 iα、iβ分别为两相坐标系下的定子电流,np为极对数。
转矩脉动与定子磁链脉动估算式为:
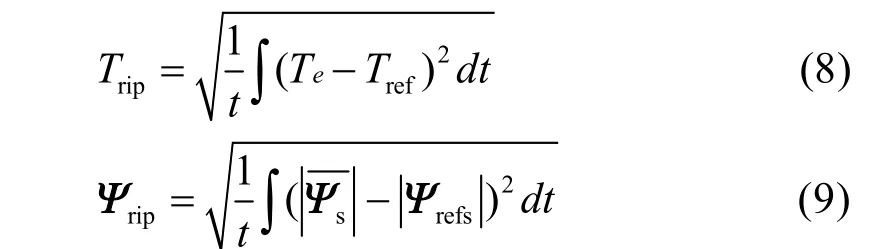
这里 Tref、Te、Ψs、Ψsref分别表示电机处于某种状态下的电磁转矩估算值、转矩参考值、定子磁链估算值和定子磁链参考值。
4 仿真验证
本文所提出双PI SVM-DTC优化控制策略将在Matlab/Simulink环境下进行对比验证。为了方便,传统直接转矩策略、基于空间电压矢量直接转矩控制策略和双 PI直接转矩优化控制策略将分别用“传统DTC”、“SVM-DTC”和“SVM-DTC1”表示。
仿真所用永磁同步电机和系统参数如下:极对数为8,额定功率4.088 MW,额定电压660 V,定子电阻0.001502 Ω,定子电感为0.0004767 H,转动惯量1200 kg∙m2,给定定子磁链幅值3.6Wb,直流母线电压931 V,额定转速为150 r/min。
图6、图7所示为电机运行于额定转速时三种控制策略的定子磁链波形与电磁转矩波形图。

图6恒转速恒转矩下传统 DTC、SVM-DTC、SVM-DTC1定子磁链波形

图7 传统 DTC、SVM-DTC、SVM-DTC1在额定转速下转矩波形
从图5、图6可以看出,电机额定转速运行时,SVM-DTC和SVM-DTC1的转矩脉动和定子磁链脉动与传统 DTC相比都大幅的减小,SVM-DTC1具有最小的转矩脉动。虽然三种方案中,SVM-DTC拥有最小的定子磁链脉动,但在使用直接转矩控制技术的电力传动系统中,转矩脉动减小更为重要,因此在三种直接转矩控制方案中,本文提出的方案具有最优的稳态性能。
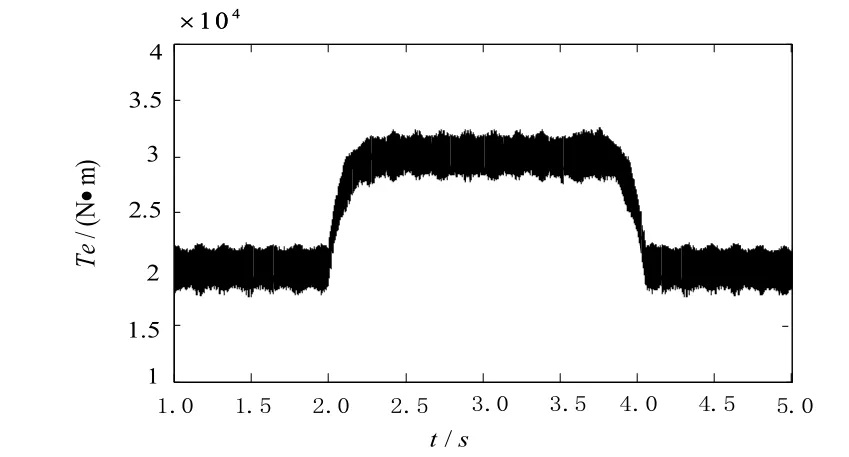
图8 恒转速变转矩下SVM-DTC1的转矩波形
图8为恒转速变转矩下SVM-DTC1的转矩波形。仿真时间为7 s,转速给定值为150 r/min,仿真起始时,电机带2×104Nm的负载转矩启动,在2.0 s时,将负载转矩突增至3×104Nm,在4.0 s时,将负载转矩突减至2×104Nm。由此可见,新的优化控制策略在恒转速变转矩工况下可以得到应用。
图9为电力推进直接转矩控制系统在恒转矩变转速下SVM-DTC1的转速波形,转速按照船舶车钟设定,即 Start(起动)→Half(半速前进,75 r/min)→Full(全速前进,150 r/min)→半速前进(Half)模拟船舶运动[15]。图10为对应转矩波形图,负载转矩给定值为2×104Nm。推进电机在0 s时启动(Start),电磁转矩突增,启动时车钟推到半速(Half),经过0.5 s,电机启动完毕,转速稳定在75 r/min,转矩稳定在2×104Nm;车钟在3 s推至全速前进(Full),3.5 s时转速稳定在150 r/min,转矩稳定在2×104Nm;在5 s车钟推至半速前进(Half),转矩突降,减速过程中转矩稳定在1×104Nm,转速稳定在75 r/min时,转矩突增并稳定在2×104Nm。由此可见,本文提出的双PI SVM-DTC策略在于电力推进系统变速航行工况中依然可以得到应用,系统动态性能得到了优化。
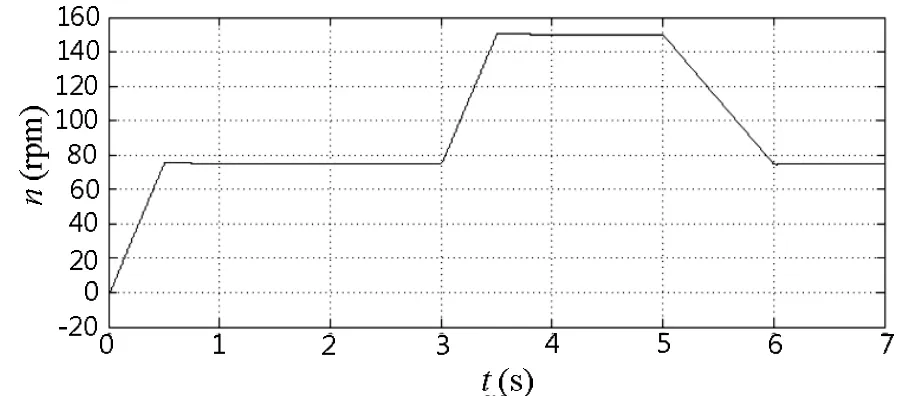
图9 恒转矩变转速下SVM-DTC1的转速波形
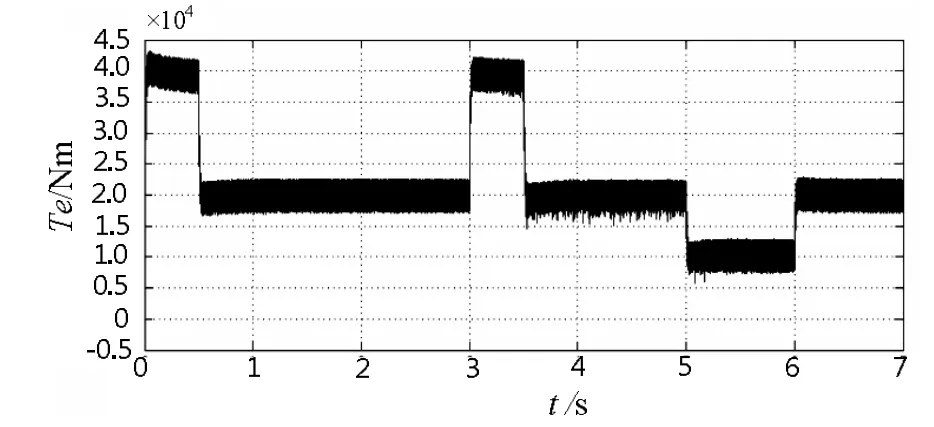
图10 恒转矩变转速下SVM-DTC1的转矩波形
5 结语
理论分析及仿真实验表明,双PI SVM-DTC优化控制策略可以应用在永磁同步电机直接转矩控制系统中,且具有有效抑制转矩脉动的调节作用,改善了系统的稳态和动态响应性能。特别在具有大容量和大转动惯量的船舶电力推进系统中,双PI SVM-DTC优化控制策略与传统直接转矩控制(DTC)和基于空间矢量调制的传统直接转矩控制(SVM-DTC)策略相比,转矩脉动最小,优化控制效果明显,有重要的理论和现实意义。
[1] Takahashi I, Noguchi T. A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor[J]. IEEE Transactions on Industry Applications, 1986, 22(5): 820 - 827.
[2] M.Depenbrock. Direct self-control (DSC) of inverter-fed induction machine[J]. IEEE Transactions on Power Electronics, 1988, 3(4): 420-429.
[3] 赵宏革. 基于船舶电力推进系统直接转矩控制技术研究[D]. 大连: 大连海事大学, 2011.
[4] Shyu K K, Lin J K, Pham V T, et al. Global Minimum Torque Ripple Design for Direct Torque Control of Induction Motor Drives[J]. IEEE Transactions on Industrial Electronics, 2010, 57(9): 3148-3156.
[5] G. Abad, M. A. Rodriguez and J. Poza.Two-level VSC based predictive direct torque control of the doubly fed induction machine with reduced torque and flux ripples at low constant switching frequency[J]. IEEE Trans. Power Electron, 2008, 23(3): 1050–1061.
[6] 杨影, 陈鑫, 涂小卫, 等. 占空比调制的永磁同步电机直接转矩控制[J]. 电机与控制学报, 2014(4):66-71.
[7] Zhu H, Xiao X, Li Y. Torque Ripple Reduction of the Torque Predictive Control Scheme for Permanent-Magnet Synchronous Motors[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 871-877.
[8] 高儒, 葛兴来. 基于间接定子量的永磁同步电动机三电平直接转矩控制[J]. 微特电机,2015,02: 39-43.
[9] Zhang Y, Zhu J, Zhao Z, et al. An Improved Direct Torque Control for Three-Level Inverter-Fed Induction Motor Sensorless Drive[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1-1.
[10] 周贤娟, 冯梅琳, 韩树人. 基于模糊控制的异步电动机直接转矩控制系统研究[J]. 江西理工大学学报, 2014, (3): 51-55.
[11] 徐艳平, 雷亚洲, 马灵芝, 等. 基于模糊参数优化的 PMSM 反推直接转矩控制[J]. 电气传动, 2015, 45(12): 12-16.
[12] 李彦, 唐智星. 船舶电力推进DTC系统低速性能的改善研究[J]. 科学技术与工程, 2013, 13(7): 1773-1778.
[13] Foo G, Rahman M F. Sensorless Direct Torque and Flux-Controlled IPM Synchronous Motor Drive at Very Low Speed Without Signal Injection[J]. IEEE Transactions on Industrial Electronics, 2010, 57(1): 395-403.
[14] 赵欣欣. 船舶车钟系统设计与实现[D]. 大连: 大连海事大学, 2013.
Optimization of SVM-DTC for Permanent Magnetic Motor in Ship Electric Propulsion
Li Yunpeng, Zhao Hongge, Li Shilin, Sun Junhao, Feng Yang
(School of Marine Engineering, Dalian Maritime University, Dalian 116026, China)
In order to reduce the torque ripple that exists in direct torque control of permanent magnet synchronous in ship electric propulsion, a new direct torque control plan based on space vector modulation is proposed. This plan mainly uses two PI regulators to control the angle and amplitude of the voltage vector respectively, synthesized by space vector modulation. With simple structure and stronger robust, the proposed plan optimization effect is obvious, which reduces torque ripple significantly and improves steady performance and dynamic of the permanent magnet synchronous motor in ship power system. The simulation result verifies the feasibility and validity of the plan.
marine electric propulsion; direct torque control; space vector modulation; PI regulator; torque ripple
U665.13
A
1003-4862(2017)02-0025-05
2016-08-12
李云鹏(1989-),男,硕士,研究方向:电力电子与电力传动。E-mail:glofindal@qq.com
赵宏革(1967-),男,博士,教授,研究方向:电力电子与电力传动。E-mail:zhaohg@dlmu.edu.cn

