建筑体型廓线对建筑物表面粒子沉积特性的影响

华凤皎， 亢燕铭， 钟 珂

(东华大学 环境科学与工程学院，上海 201620)

建筑体型廓线对建筑物表面粒子沉积特性的影响

华凤皎， 亢燕铭， 钟 珂

(东华大学 环境科学与工程学院，上海 201620)

选取典型建筑体型，利用计算流体力学方法研究了建筑体型对气溶胶粒子在建筑表面沉积速度和沉积通量的影响．结果表明：迎风面宽度是影响气溶胶粒子在建筑表面沉积速度和沉积通量的重要因素，且迎风面和背风面对其的影响规律不同；建筑表面上气溶胶粒子的沉积通量随着其粒径的变化而变化，且不同建筑表面最小沉积通量对应的粒径不同．

建筑体型； 建筑外表面；惯性沉积； 沉积速度； 沉积通量； 气溶胶粒子

目前，城市大气霾污染已成为我国重要的环境问题．工业过程、机动车尾气以及其他人类活动产生的气溶胶粒子，不仅对人体健康产生威胁，也将对建筑物、构筑物以及其他各种市政设施产生严重污染腐蚀和损害，如建筑表面的粒子沉积会影响其围护结构的热工性能及美观要求．近几年，随着霾天气在我国大范围地区的频繁出现，这种气溶胶污染效应也变得越发严重．即使大气中有害气溶胶已被有效清除，沉积在建筑物表面的粒子仍然会长时间地影响建筑物附近的空气质量．为了减少气溶胶粒子造成的危害，须对这些粒子沉积特征有清楚的认识．此外，古建筑的保护也需要了解和预测建筑各表面的粒子沉积情况，通过对建筑物墙体进行及时清洗，减弱气溶胶对文物和古迹的腐蚀．

粒子在固体表面的沉积特性研究报道较多.如文献[1]给出了封闭空间内均匀湍流粒子沉积的解析解．文献[2]对粒子的沉积速度进行了参数化分析，给出了计算粒子干沉积速度的简化公式．文献[3]采用多层箱体模型模拟了包含多种地表形态的大尺度区域粒子的沉积通量，但并没有求解区域内的流动情况．文献[4]采用离散轨迹模型研究了不同通风房间内粒子的质量浓度分布和沉积特性．文献[5]研究了城市环境下垫面、建筑物墙体和屋顶的气溶胶粒子沉积速度，指出仅用一个或几个物理量来表示城市气溶胶粒子沉积速度的方法过于简化了对问题的分析．

上述文献侧重于研究粒子沉积速度与气流分布的关系以及室内粒子的沉积，均没有考虑建筑体型对室外粒子在墙面沉积的影响．通常情况下，粒子的沉积效应主要受扩散和惯性的共同作用[6]．由于不同建筑物体型对气流的阻挡效应和其周围流场特征不同，导致了粒子在不同体型建筑周围随气流运动时的动力学行为的差异．

为考察不同的建筑体型廓线下粒子在建筑物表面的沉积特征，本文将针对城市中常见的点式建筑和条形建筑体型，采用计算流体力学方法构建粒子沉积模型，分析建筑体型对其围护结构外表面上的粒子沉积特性的影响．

1 数值计算模型和方法

1．1 数值计算模型

表1给出了典型建筑体型的特征参数，其中，建筑体型尺寸长为L，宽为W，高度为H．计算区域的大小对于计算量和模拟结果的准确性会造成影响，当计算区域长度和高度不小于建筑物高度的5～6倍时，可消除边界效应对计算结果的影响[7-8]．因此，本研究中计算区域高度取为6H，入口距建筑物迎风面的距离为5H，出口距建筑物背风面距离为10H．本文建筑体型case 2 L的计算区域如图1所示．

表1 建筑体型尺寸

图1 模型计算域及网格示意图Fig．1 Schematic diagram of the computational domain and enlarged mesh

采用Gambit软件对求解区域进行非结构化网格划分，并对建筑外表面附近区域进行网格局部加密处理，而其他区域则采用正常尺寸网格来优化整体网格数量并节约数值计算成本．模拟计算前，进行了网格独立性检验，即增加网格数，直至网格数的增加对计算结果没有影响为止[9]．经检验，最终网格数量为163～291万．

1．2 计算方法和边界条件的设定

湍流流场可以采用不同的湍流模型进行模拟，为节约计算成本并获得简洁合理的数值结果，根据文献[10-13]可知，标准κ-ε模型能很好地模拟本文条件下的湍流流场，其中壁面湍流特征用标准壁面函数描述，采用有限容积法离散控制方程，并对动量、湍流动能κ、能量耗散率ε的输运方程采用二阶迎风格式进行差分，以提高计算精度．

污染物输送质量浓度变化的对流扩散方程为

(1)

式中：Ci为污染物质量浓度；K为粒子扩散系数；Si为污染源项；uj为j方向的速度分量；xj为笛卡尔坐标分量．

计算域的进口边界条件设为速度入口，风速大小采用速度廓线形式．风速的垂直特性与地形及地面粗糙度有关，速度廓线可由指数律分布[14-16]表示，如式(2)所示．

(2)

式中：z为任一高度， m；zs为参考高度， m；u(zs)为zs处的参考风速， m/s， 考虑到城市区域的稳定气象条件，本文取20 m高度处的风速为2 m/s；α为地面粗糙系数(风剖面幂指数)，本文α取0．25[17-18]．速度廓线采用C++语言用户编程并与Fluent程序提供的UDF(user-defined functions)对接．

计算区域出口处可视为充分发展的湍流，采用出流边界条件(outflow)，即该流出区域的质量流率和流入区域的质量流率相等．建筑表面及地面采用无滑移条件，其余各面则采用滑移速度边界．

假设城市背景气流中粒子质量浓度均匀，因此，设每种粒径粒子在计算域进口处空气中的质量浓度为10 μg/m3．城市大气中，气溶胶粒子的粒径范围很广，生物有害性粒子尺寸(空气动力学直径)通常在1～10 μm范围，其中2 μm左右及以下的粒子占绝大多数[3]，粒子密度约为1 300 kg/m3[19]．故本文选取粒子密度取ρp= 1 500 kg/m3，对粒径dp=0．5， 1．0， 1．5， 2．5， 3．5， 5．0， 7．0和10．0 μm分别进行计算和分析．

1．3 粒子输运理论基础和计算方法

粒子在空气中的输运模拟采用欧拉法，选用混合模型求解第二相粒子的动量和体积分数．大气环境中粒子可视为稀薄相，只考虑流场对颗粒物的单向耦合作用．壁面处的粒子沉积通量J可用式(3)计算．

(3)

式中：CVOF-dA为靠近壁面控制体中粒子相体积分数；vd-dA为某一点粒子的沉积速度； dA为控制体壁面的面积；Awall为建筑物表面面积．

建筑物不同外表面上的粒子沉积速度vd为垂直面上的沉积速度vdv

(4)

朝上的水平面沉积速度vdu

(5)

式中：vs为粒子的终端沉降速度， m/s；u*为摩擦速度， m/s； 参量I的具体表达式见文献[20]；u*为通过流体的湍流动能k， m2/s，由式(6)计算得到．

(6)

1．4 数值模型的合理性验证

为了保证数值模拟方法分析建筑流场分布特征的可靠性，需要对所采用数学模型进行验证．本文利用汉堡大学气象研究所提供的BLASIUS风洞试验数据库[21]对速度场进行验证．模拟参数与试验保持一致，模型采用边长为125 mm的立方体，入口风速采用速度廓线，参考高度500 mm处的参考风速为6 m/s，风速廓线指数为0．22．采用文献[22]的试验结果验证浓度场，具体如下：风洞中的模型尺寸为60 mm×60 mm，其长度与风洞长度相等，充分发展区的风速廓线指数为0．20，参考高度650 mm处的参考风速为3 m/s．污染物质量浓度采用无因次浓度C*来表示，如式(7)所示．

(7)

式中：Ci为i点处的污染物质量浓度， kg/m3；q0为污染物散发强度， kg/s；Ls为污染源长度，取0．9 m．

建筑迎风区和背风区的数值计算结果与风洞试验结果如图2所示，其中u(z)为沿无量纲高度Z(Z=z/H)方向的气流速度分量．由图2(a)可以看出，本文模拟结果在建筑物高度范围内与风洞试验结果吻合得比较好．图2(b)给出的污染物质量浓度分布验证说明，迎风区质量浓度计算值与实测值符合得较好，背风区几乎完全吻合．因此，本文采用的数值模型可以很好地预测城市中单体建筑物附近的气流流动状况和粒子质量浓度分布情况．

(a) 气流速度

(b) 质量浓度

2 模拟结果与分析

2．1 建筑体型对建筑附近气流速度的影响

对表1给出的各建筑体型逐一进行了模拟．在case 1L和case 3L两种典型情况下，在z=5 m高度处建筑周围的气流流线分布如图3所示．

图3 典型建筑z=5 m平面上的气流流线分布Fig．3 Streamline distributions on typical planes of the buildings at z=5 m

由图3可以看出，由于建筑物对来流的阻挡，导致在建筑侧面及背风面区域均会形成涡流．由于case 3L的迎风面宽度较大，其背风面形成的回漩涡流区域也明显大于case 1L． case 3L侧面近壁区完全处于涡流状态，而case 1L侧面较长，涡流主要分布在扰流区前端．二次流的分布不同可能会导致粒子沉积到建筑物表面的概率不同，从而造成建筑表面粒子沉积通量的差异．图3还表明，不同体型的建筑物附近的气流流动速度不同，可能会导致建筑物不同表面的粒子沉积速度有所不同．

为定量分析建筑各表面附近气流速度的差异，图4给出了距离建筑物背风面、迎风面和侧面0．25 m处投影平面的垂直中心线上气流速度沿无量纲高度Z的变化情况．

(a) 迎风面

(b) 背风面

(c) 侧面

由图4(a)可见，在迎风面附近，高度相同、体型不同的建筑物附近气流速度变化曲线相似，仅在Z<0．3的近地区域略有不同．高度不同的建筑物附近气流速度变化趋势也基本一致，这表明建筑体型和高度对迎风面中心附近气流速度的影响很小．从图4(b)和4(c)中可看出，建筑物背风面和侧面的气流速度受建筑体型和迎风面宽度影响很大．不同体型的建筑物背风面在Z<0．3的近地区域气流速度基本相等，上部流速随着迎风面宽度增大而增大，且建筑物越高，规律越明显．另外，较高建筑的背风区气流速度也高于相同平面结构的较低建筑．

由图4(c)还可以看到，在case 2L/case 2H和case 3L/case 3H两种情况下，建筑侧面近地区域的气流速度很接近，且远大于case 1L/case 1H的气流速度．这是因为前者建筑侧面尺寸较小，建筑侧面完全位于涡流区内，流速受涡流影响而明显增大，而后者侧面部分的前端区域位于涡流区内，而所考察的速度样本点位置已在涡流区外，故气流速度较小．这一差别将会对粒子在建筑物表面的沉积特性产生影响．

2．2 建筑各表面上的粒子沉积通量

由数值模拟结果和式(3)沉积通量的计算可以得到表1中6种情形的迎风面、侧面、背风面和屋顶上粒子沉积通量J与粒径dp的关系，结果如图5所示．

由图5(a)可知，不论建筑高低，均表现为迎风面越宽，迎风面上的沉积通量越小，此外，粒子粒径越小，沉积通量受建筑体型影响越小.这是因为小粒子的沉积主要受扩散机理控制，而大粒子的沉积主要受惯性力控制．由于建筑体型是通过影响周围流场来影响粒子沉积效果的，因此只能影响到受惯性力控制的大粒子的沉积效果．

(a) 迎风面和侧面

(b) 背风面

(c) 屋顶

(d) 建筑物总表面

另外，比较不同建筑体型中迎风面最小沉积通量对应的粒子直径可以看到，除了迎风面面积较小的case 1H迎风面上的最小沉积通量对应粒径为2．5 μm外，其他体型建筑对应粒径均为3．5 μm．这是因为case 1H对气流的阻挡作用小，迎风面附近气流平均速度大于其他建筑体型的情况，粒子受到的惯性作用大，故导致最小沉积通量对应的粒径小于其他建筑体型．由图5(a)还可以看到，虽然侧面粒子沉积通量略小于迎风面，但沉积通量随粒径的变化曲线与迎风面非常相似，最小沉积通量对应的粒径也是3．5 μm．

由图5(b)可见，背风面上沉积通量随粒径的变化规律为，迎风面越宽，背风面粒子沉积通量越大．此外，对比图5(a)和5(b)还可以看到，背风面上的沉积通量明显小于迎风面，同时最小沉积通量对应粒径较大，约为5．0～7．0 μm．这是因为背风面附近气流速度远低于迎风面，故粒子在这里受到的惯性力较小，于是最小沉积通量对应的dp必然增大．由图5(c)可看出，在重力沉降的作用下，屋顶上的沉积通量随着粒径的增加单调上升．由于屋顶表面附近的局地风速受建筑体型的影响较小，故不同建筑体型的沉积通量差别很小．由图5(d)可知，由于屋顶水平面上的沉积通量远大于其他垂直表面的沉积通量，建筑物表面总的沉积通量主要取决于屋顶上的沉积通量，因此，其与屋顶上呈现出相同的沉积规律．

2．3 建筑体型对沉积速度的影响

根据气溶胶动力学原理[23-24]，粒子的沉积速度与建筑物附近气流速度密切相关．为了对建筑物表面沉积情况进行总体评价，在距离建筑物表面0．25 m的投影平面上均匀取点，每个点间距1 m，取值点总数为442～2 502，提取这些取样点处的数值结果来讨论气溶胶粒子在外墙面的沉积规律． 根据流场的数值模拟结果和式(4)和(5)，在不同建筑体型下，dp=0．5和10．0 μm的粒子在建筑迎风面、背风面、侧面和屋顶上的沉积速度统计结果如图6所示．

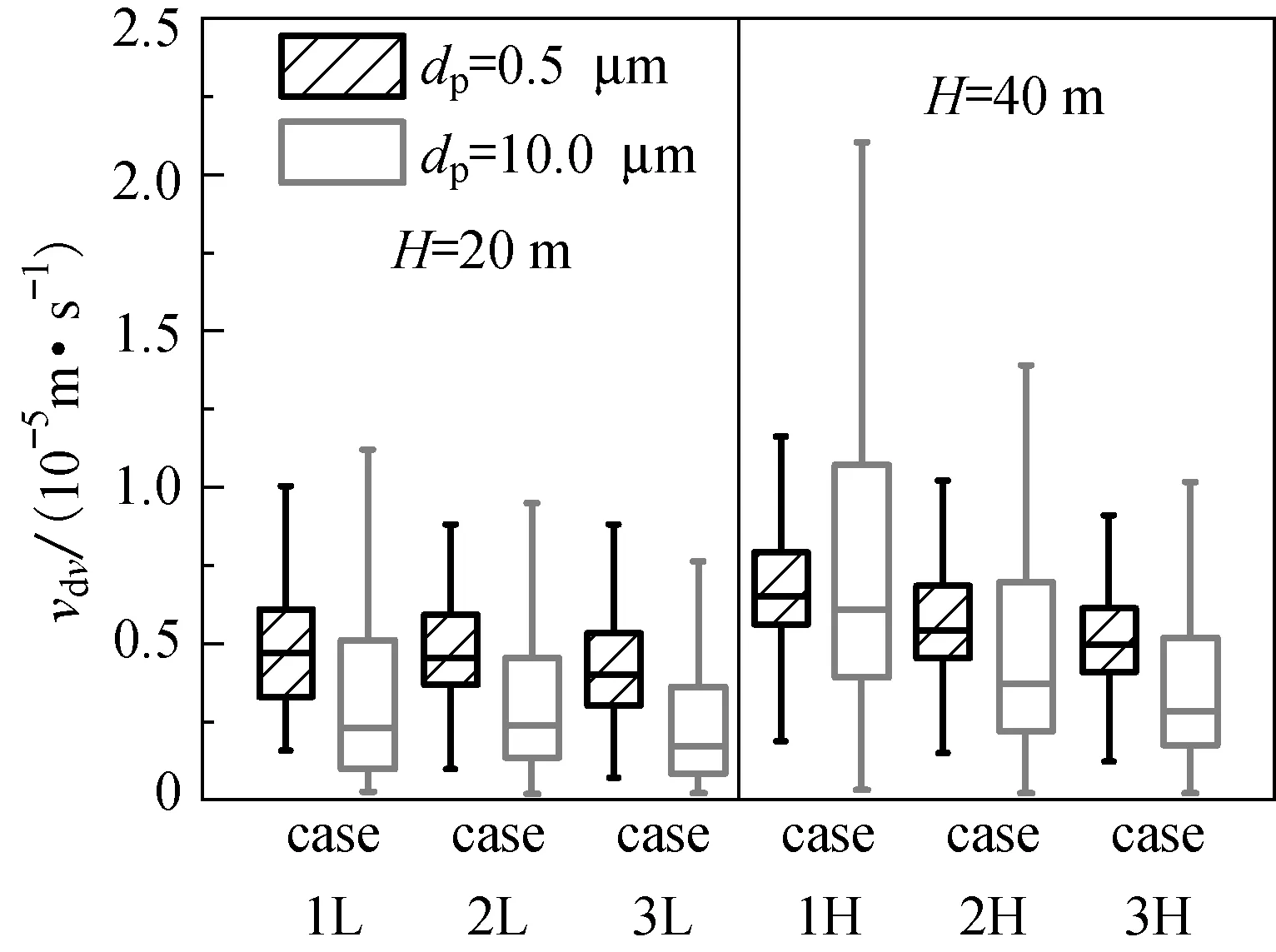
(a) 迎风面

(b) 背风面

(c) 侧面

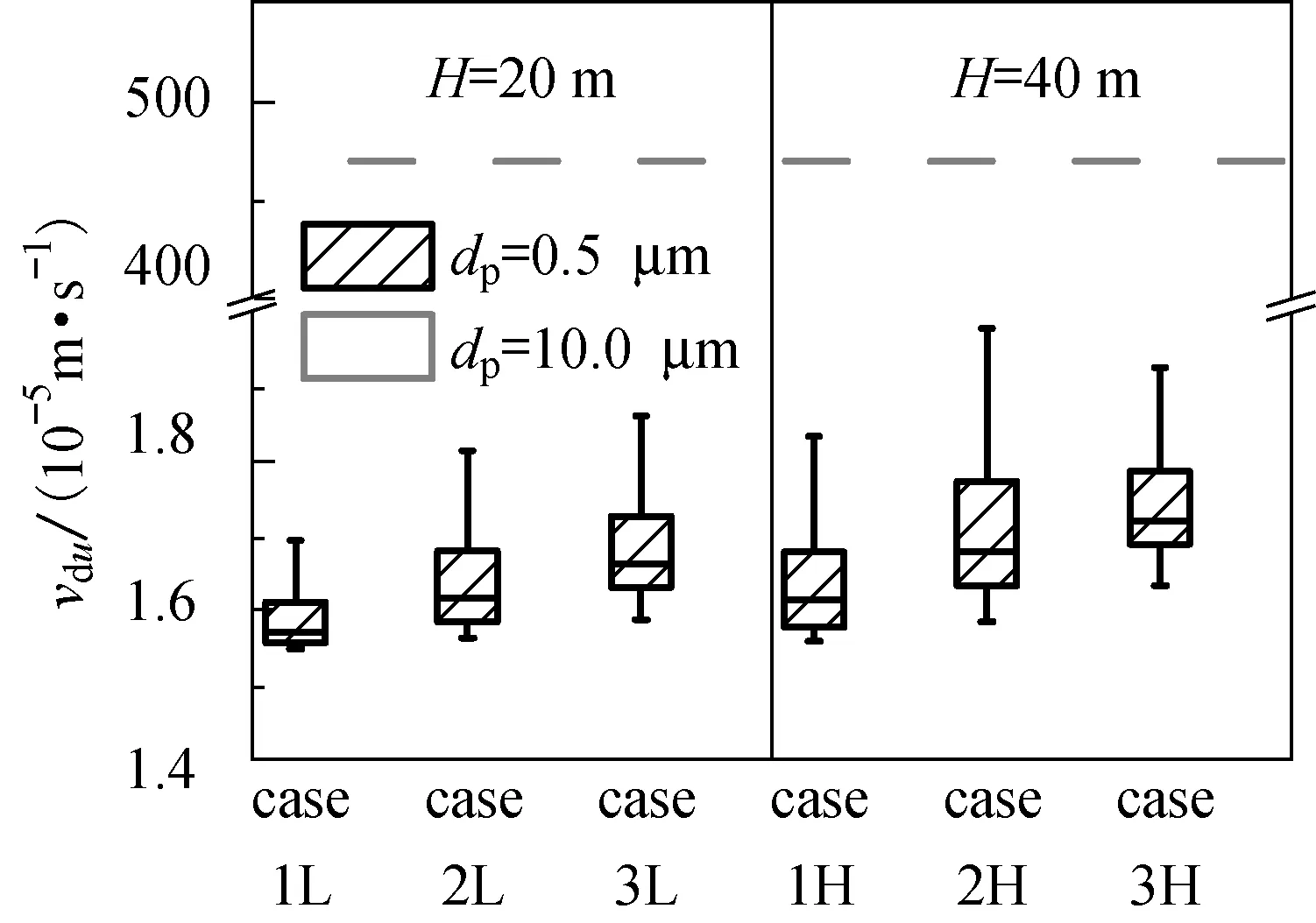
(d) 屋顶

由图6(a)可见，在两种建筑高度下，均表现为迎风面越窄，粒子沉积速度越大的特征．由图6(b)可知，背风面与迎风面表现出的规律则恰好相反．这一规律在高建筑(即H=40 m)上表现得更为明显．这可能是由于迎风面尺度越大，背风区的湍动能亦越大，故式(6)中的摩擦速度将增加，从而使得沉积速度增大．

图6(c)中表明，粒子在建筑侧面上沉积速度与迎风面沉积速度在量级上相当，但与建筑体型和迎风面宽度的关系并没有非常明确的相关性．这很可能是因为，不同体型的侧面宽度不同，而建筑侧面空气流动情况受到迎风面和侧面尺寸的共同影响．由图6(d)可见，dp=10．0 μm的粒子在屋顶上的水平沉积速度明显高于dp=0．5 μm粒子的沉积速度.这是因为大粒子还会受到重力沉积的作用，从而强化了大粒子的沉积．此外，屋顶上的沉积速度与建筑体型和迎风面宽度的相关性与背风面相同，即沉积速度随着迎风面宽度的增大而增大．综合以上分析，可以认为迎风面宽度W与沉积速度vdv存在明确的相关性．

为评价建筑物迎风面宽度W对粒子沉积效果的影响，现以迎风面宽度最小的case 1L和case 1H为基准，定义其他建筑模型表面不同dp粒子的沉积速度和沉积通量变化率η，如式(8)所示．

(8)

式中：Y代表沉积速度vdv或沉积通量J；x=2， 3，分别为表1所示的case 2和case 3类型的建筑；i=L， H，分别表示低建筑和高建筑．

根据以上定义，图7给出了不同建筑体型迎风面上的粒子沉积通量变化率η与其粒径的关系．

图7 不同建筑迎风面上不同粒子沉积通量 变化率随其粒径的变化Fig．7 Changed ratios of deposition flux with dpon windward of different buildings

由图7可以看到，建筑迎风面宽度的增大将使得所有粒径的粒子在迎风面的沉积通量均产生不同程度的减小，这与上述迎风面宽度对粒子沉积速度的影响的结论相吻合．由图7还可以看到，迎风面宽度对粒子沉积通量的影响程度随着粒径和建筑高度的增大而增加．

为了比较建筑体型对粒子沉积速度和沉积通量的影响程度，图8分别给出了dp=0．5和10．0 μm的粒子在建筑迎风面和背风面上沉积速度与沉积通量变化率η．

(a) 迎风面

(b) 背风面

由图8(a)可以看到，迎风面上的粒子沉积速度与沉积通量的变化率η的变化规律保持一致，随着迎风面宽度和建筑高度的增加，迎风面上的粒子沉积速度和沉积通量都减小，且粒径越大越明显．由图8(b)可以看到：对于较高的建筑，迎风面宽度较大的体型使得背风面上大粒子和小粒子沉积速度和沉积通量都增大，但沉积通量的增大幅度明显低于沉积速度；对于较低建筑，背风面沉积速度随着迎风面宽度增大而增加，但沉积通量却出现了减小现象．这是因为沉积通量由沉积速度和粒子质量浓度共同决定，沉积通量没有完全随着沉积速度的增大而增加，这可能是建筑表面粒子质量浓度随迎风面宽度变化的规律与沉积速度不一致造成的．为此，图9给出了不同建筑体型下建筑中心剖面上dp=0．5 μm粒子的质量浓度分布．

图9 不同建筑体型中心剖面上的粒子质量浓度分布Fig．9 Particle concentration distributions on centre section of different buildings

由图9可以看到，由于沉积效应对粒子的清除作用，随着迎风面宽度的增大，背风面附近的粒子质量浓度下降，因此，使得粒子沉积通量随迎风面宽度增加的幅度减小(对于较高建筑)．尽管随着建筑迎风面宽度增加，粒子沉积速度增大，但当沉积速度的增大量不足以抵消粒子质量浓度的减小量时，沉积通量随迎风面宽度增大的变化趋势就不再与沉积速度相同．

3 结 语

建筑物表面的粒子沉积不仅严重影响建筑外观，而且在雨雪冲刷和太阳辐射的共同作用下，还会因外墙材料的腐蚀而改变围护结构的热工特性和室内热环境．由于建筑物的体型对其周围流场有重要的畸变作用，进而影响到随背景空气输送的大气气溶胶在建筑物表面上的沉积特性，但相关的研究还很缺乏．因此，本文应用粒子沉积模型和计算流体力学方法，对几种典型体型廓线的建筑表面上粒子沉积特性进行了数值计算和分析，讨论了不同表面上发生粒子沉积的特征．主要结论如下：

(1) 由于不同体型建筑对来流的阻挡作用不同，形成了不同的流场特征．本文模拟结果表明，建筑迎风面尺寸对流场的影响作用大于建筑高度的影响效果．因此，建筑高度增大虽然增大了迎风面面积，但对粒子沉积速度的影响没有迎风面宽度变化的作用明显．

(2) 随着建筑物迎风面宽度的增大，建筑迎风面上粒子沉积速度将会下降，但在背风面上的沉积速度则会升高．建筑物迎风面上的粒子沉积通量随迎风面宽度的变化规律与沉积速度一致，但对于背风面，由于墙面附近粒子质量浓度受迎风面宽度的影响趋势与沉积速度不同，沉积通量与沉积速度变化规律不完全一致．

(3) 由于不同建筑表面附近气流惯性作用不同，故不同表面上最小沉积通量对应的粒径也不同．由于背风面处在建筑尾流区，气流平均速度低，故粒子的惯性和湍流扩散效应均较弱，因此，背风面最小沉积通量对应的粒径将大于迎风面和侧面．

[1] CORNER J， PENDLEBURY E D． The coagulation and deposition of a stirred aerosol[J]． Proceeding of the Physical Society， 1951，64(8)：645-654．

[2] ZHANG L， GONG S， PADRO J， et al． A size-segregated particle dry deposition scheme for an atmospheric aerosol module[J]． Atmospheric Environment， 2001，35(3)：549-560．

[3] MONFORTI F， BELLASIO R， CLAI G， et al． An evaluation of particle deposition fluxes to cultural heritage sites in Florence， Italy[J]． Science of the Total Environment， 2004，334/335(1)：61-72．

[4] ZHAO B， ZHANG Y， LI X T， et al． Comparison of indoor aerosol particle concentration and deposition in different ventilated rooms by numerical method[J]． Building and Environment， 2004，39(1)：1-8．

[5] JONSSON L， KARLSSON E， JONSSON P． Aspects of particulate dry deposition in the urban environment[J]． Journal of Hazardous Materials， 2008，153(1)：229-243．

[6] GREENFIELD S M． Rain scavenging of radioactive particulate matter from the atmosphere[J]． Journal of Atmospheric Sciences， 1957，14(2)：115-125．

[7] TOMINAGA Y， MOCHIDA A， YOSHIE R， et al． AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings[J]． Journal of Wind Engineering and Industrial Aerodynamics， 2008，96(10)：1749-1761．

[8] NAKAMURA Y，OKE T R． Wind temperature and stability conditions in an east-west oriented urban canyon[J]． Atmospheric Environment， 1988，22(12)：2691-2700．

[9] LEI Y G， HE Y L． Effects of baffle inclination angle on flow and heat transfer of a heat exchanger with helical baffles[J]． Chemical Engineering and Processing： Process Intensification， 2008，47(12)：2336-2345．

[10] LAUNDER B E， SPALDING D B． The numerical computation of turbulent flows[J]． Computer Methods in Applied Mechanics and Engineering， 1974，3(2)：269-289．

[11] NAZRIDOUST K， AHMADI G． Airflow and pollutant transport in street canyons[J]． Journal of Wind Engineering and Industrial Aerodynamics， 2006，94(6)：491-522．

[12] DI SABATINO S， BUCCOLIERI R， PULVIRENTI B， et al． Flow and pollutant dispersion in street canyons using FLUENT and ADMS-Urban[J]． Environ Mental Modeling & Assessment， 2007，13(3)：369-381．

[13] NG W Y， CHAU C K． A modeling investigation of the impact of street and building configurations on personal air pollutant exposure in isolated deep urban canyons[J]． Science of the Total Environment， 2014，468/469：429-448．

[14] CHEUNG J O P， LIU C H． CFD simulations of natural ventilation behaviour in high-rise buildings in regular and staggered arrangements at various spacings[J]． Energy and Buildings， 2011，43(5)：1149-1158．

[15] LEUNG K K， LIU C H， WONG C C C， et al． On the study of ventilation and pollutant removel over idealized two-dimensional urban street canyons[J]． Building Simulation， 2012，5(4)：359-369．

[16] RAJAPAKSHA I， NAGAI H， OKUMIYA M． A ventilated courtyard as a passive cooling strategy in the warm humid tropics[J]． Renewable Energy， 2003，28(11)：1755-1778．

[17] MOHAMED F Y．A wind tunnel study on the effect of thermal stability on flow and dispersion of rooftop stack emissions in the near wake of a building[J]． Atmospheric Environment， 2013，65：89-100．

[18] WANG H J， CHEN Q Y． A new empirical model for predicting single-sided， wind-driven natural ventilation in buildings[J]． Energy and Buildings， 2012，54：386-394．

[19] TISA L S， KOSHIKAWA T， GERHARDT P．Wet and dry bacterial spore densities determined by buoyant sedimentation[J]． Applied and Environmental Microbiology， 1982，43(6)：1307-1310．

[20] LAI A C K， NAZAROFF W W． Modeling indoor particle deposition from turbulent flow onto smooth surfaces[J]． Journal of Aerosol Science， 2000，31(4)：463-476．

[21] SCHATZMANN M． Compilation of experimental data for validation of microscale dispersion models[DB]． (1999-05-15)[2015-03-20]． http：//www．mi．zmaw．de/index．php?id=628．

[22] MERONEY R N， PAVAGEAU M， RAFADALIS S， et al． Study of line source characteristics for 2- D physical modelling of pollutant dispersion in street canyon[J]． Journal of Wind Engineering and Industrial Aerodynamics， 1996，62(1)：37-56．

[23] FRIEDLANDER S K， JOHNSTONE H F． Deposition of suspended particles from turbulent gas streams[J]． Journal of Industrial and Engineering Chemistry， 1957，49(7)：1151-1156．

[24] FUCHS N A． The mechanics of aerosols[M]． New York： Dover Publications Inc，1964：159-170．

(责任编辑：刘园园)

Effects of Building Configuration on the Particle Deposition Features on Building Surfaces

HUAFengjiao，KANGYanming，ZHONGKe

(School of Environmental Science and Engineering， Donghua University， Shanghai 201620， China)

The influences of building configuration on the deposition velocity and deposition flux of aerosol particles on the building surface were investigated by using computational fluid dynamics for typical building configurations． The numerical results show that the width of windward side of a building is a key factor to influence deposition velocity and deposition flux． Deposition velocities and deposition fluxes of aerosol particles are different on windward and leeward sides of the building． Deposition fluxes of aerosol particles on the building surfaces vary with particle diameters． Particle diameters corresponding to minimum deposition flux are also different for different building surfaces．

building configuration； building surface； inertia deposition； deposition velocity； deposition flux; aerosol particles

1671-0444(2017)01-0115-08

2016-03-23

国家自然科学基金资助项目(40975093)；上海市教委科研创新重点资助项目(14ZZ073)

华凤皎(1989—)，女，山东烟台人，博士研究生，研究方向为城市大气环境与室内空气品质. E-mail: 2111173@mail.dhu.edu.cn 钟 珂(联系人)，女，教授，E-mail:zhongkeyx@dhu.edu.cn

X 513； P 426．6

A