相控阵卫星跟踪闭环实验系统设计与实现

张江波， 李朝海， 马越， 朱虎， 张伟臻

(电子科技大学电子工程学院， 四川成都 611731)

0 引言

随着社会信息化程度的不断提高，卫星通信在导航定位、资源探测、气象服务等方面获得了广泛关注。随着卫星通信应用领域的不断拓展，许多场合要求能在运动过程中完成与卫星之间的实时通信，这使得卫星跟踪技术成为了一个研究热点[1]。

运动平台卫星跟踪系统是一个庞大而复杂的系统，其复杂性不仅体现在设计本身，其测试过程也是非常的繁琐。目前卫星跟踪系统的测试任务主要是在暗室中进行，通过手动或半自动转动平台来模拟实际运动目标在运动过程中位置的变化，从而使天线接收不同入射角度下的信号，采集板将信号采集后在PC机上进行仿真验证测角结果，而且这种测试方法无法对跟踪过程进行测试。在系统调试阶段，对跟踪系统进行实测的难度是巨大的。首先，运动平台的运动速度通常高达每小时几千米，这样高速运动的物体是很难去模拟的。此外，在测试过程中发生故障时，由于缺乏相应的数学建模，往往采取一次次查找电路图或者查看程序进行故障定位，这样不仅浪费大量的人力和时间，而且多次加电会导致设备老化，难以对故障进行及时有效的分析，并采取相应的措施。

“相控阵卫星跟踪闭环测试系统”正是基于这一需求而开发的，以期为测试人员提供一套跟踪系统结构、组成、设备分布、系统测试、系统故障分析诊断全数字化的仿真实验系统。系统尽可能真实地模拟运动物体的运动轨迹，结合跟踪系统数字板对整个跟踪过程进行仿真测试。

1 系统框架

相控阵卫星跟踪闭环实验系统包含上位机、子阵信号发生器、基带信号处理单元三个主要部分。其中，上位机模拟目标运动轨迹和运动姿态，并根据相控阵相关理论，模拟产生来波信号方向矩阵。同时，上位机接收来自基带信号处理单元的波束指向角度值，模拟产生波束指向矩阵，将来波信号方向矩阵和波束指向矩阵通过串口发送给子阵信号发生器。子阵信号发生器主要由FPGA和四路DA组成。在FPGA内置ROM中提前存放好四路相同的BPSK信号，将接收到来自上位机的来波信号方向矩阵和波束指向矩阵分别调整四路BPSK信号的幅度和相位，并将四路经过调整的信号通过DA进行输出。子阵信号发生器通过SMA接头和同轴线将模拟产生的四路信号发送给基带信号处理单元。基带信号处理单元主要由四路AD、FPGA和DSP及一些外围电路构成。基带信号处理单元对四路信号进行AD采样后送入FPGA，在FPGA中完成信号的预处理、搜索、角度估计等运算，FPGA将测角结果发送给DSP，在DSP中完成跟踪滤波，同时将角度预测值返还给FPGA。同时，FPGA将接收到的DSP返还的角度值通过串口发送给上位机，上位机通过角度值对波束指向进行调整。系统框图如图1所示。

上位机提供了清晰简洁的UI界面，在人机交互界面可以设置目标的初始位置、初速度、加速度等相关参数，上位机根据轨迹参数描绘出目标运动轨迹。同时，上位机需要设置初始波束指向，之后工作过程的波束指向由基带信号处理单元的角度预测值来更新。系统信号发生流程图如图2所示。

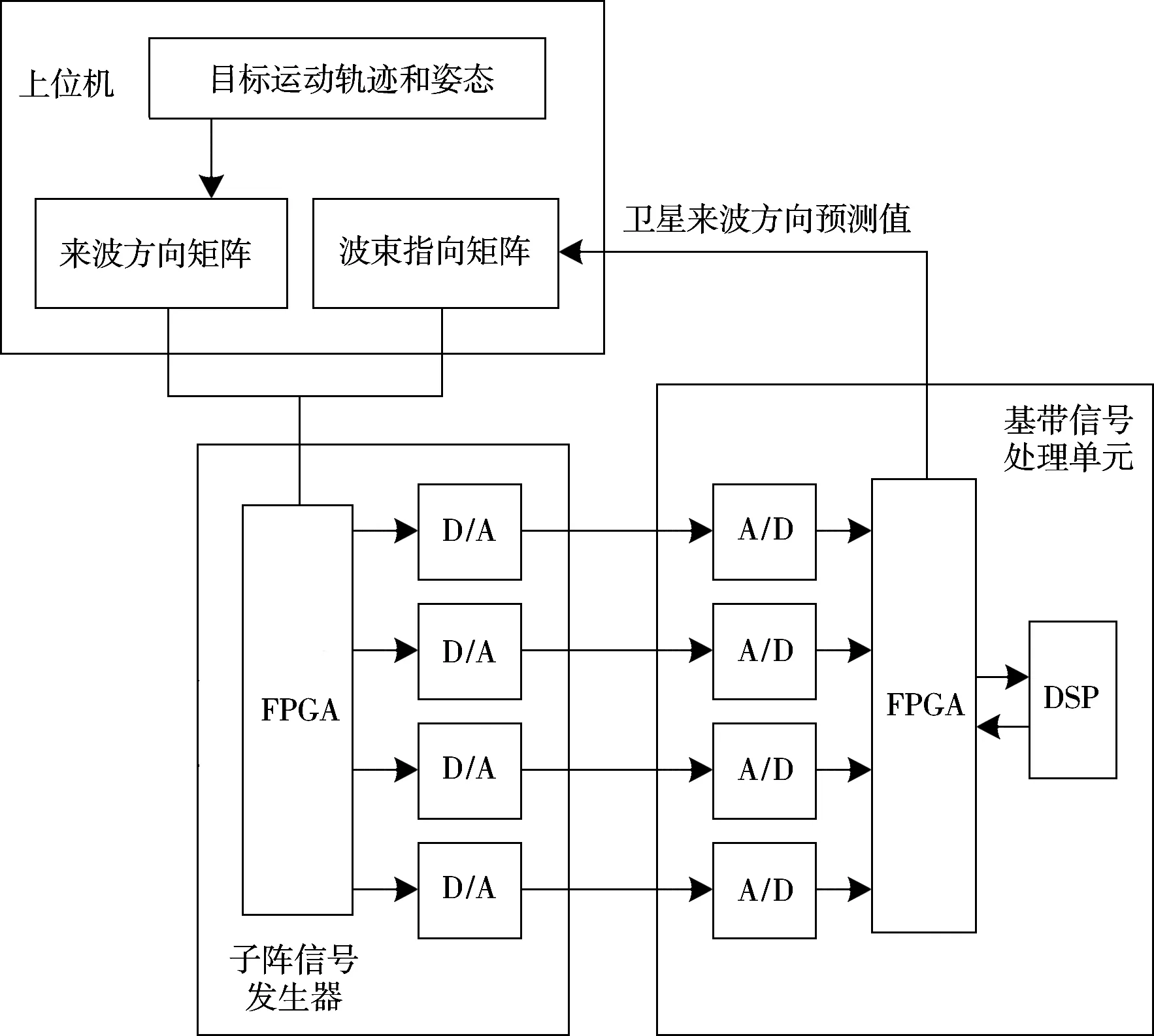
图1 卫星跟踪演示系统框图

图2 系统信号发生流程图

2 目标运动建模

本文主要研究的载体为高速、远程、平稳飞行的物体，如巡航导弹等。因此，在较短的观测周期内，可以认为目标是匀加速直线运动或匀速直线运动[2]。本节给出目标运动建模方程和对应的来波信号俯仰角和方位角，根据相控阵理论并结合工程实践推导出来波信号方向矩阵和波束指向矩阵传输形式[3]。

2.1 运动建模

首先不考虑载体姿态翻转，以载体质心作为原点，设目标相对于载体作匀速运动，沿x轴、y轴和z轴的速度分别为vx，vy和vz，在惯性系下的三个坐标轴方向的位置分别记为X(n)，Y(n)和Z(n)，n为观测时刻。观测周期为Ts，则运动方程可表示为

(1)

根据运动方程可求出目标在惯性系下归一化的方向余弦：

(2)

现在考虑载体姿态的翻转，设载体的横滚角θ、俯仰角γ和偏航角η均按照正弦形式变化。变化参数如表1所示。

表1 载体姿态变化参数

载体姿态如图3所示。

(a)载体平台横滚角

(b)载体平台俯仰角

(c)载体平台偏航角图3载机姿态

根据坐标变换原理可得到目标载体坐标系下的方向余弦，进而求解出载体坐标系下目标信号的方位角与俯仰角。设惯性系下目标沿x轴、y轴和z轴的运动速度为100，300和500 m/s，3个坐标轴的初始位置分别为500,300和1 000 km。图4给出了载体坐标系下目标方位角与俯仰角变化情况。

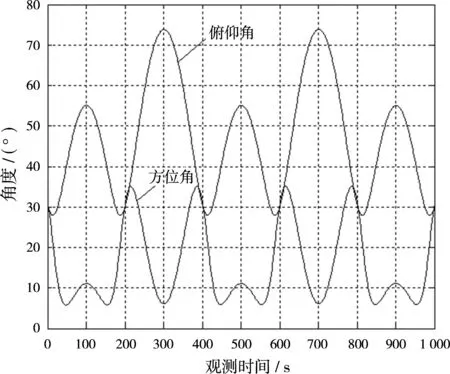
图4 载体坐标系下目标方位俯仰角变化

2.2 信号传输形式

假设均匀矩形阵列有M×N个阵元，并且被均匀分成4个子阵，阵列几何结构如图5所示，dx和dy分别表示平行于x轴方向和y轴方向上的阵元间距，Dx和Dy分别表示平行于x轴方向和y轴方向上子阵相位中心之间的间距。设平面波信号s(t)以入射方向(θ,φ)到达天线阵元，其中θ和φ分别表示入射信号的俯仰角和方位角。

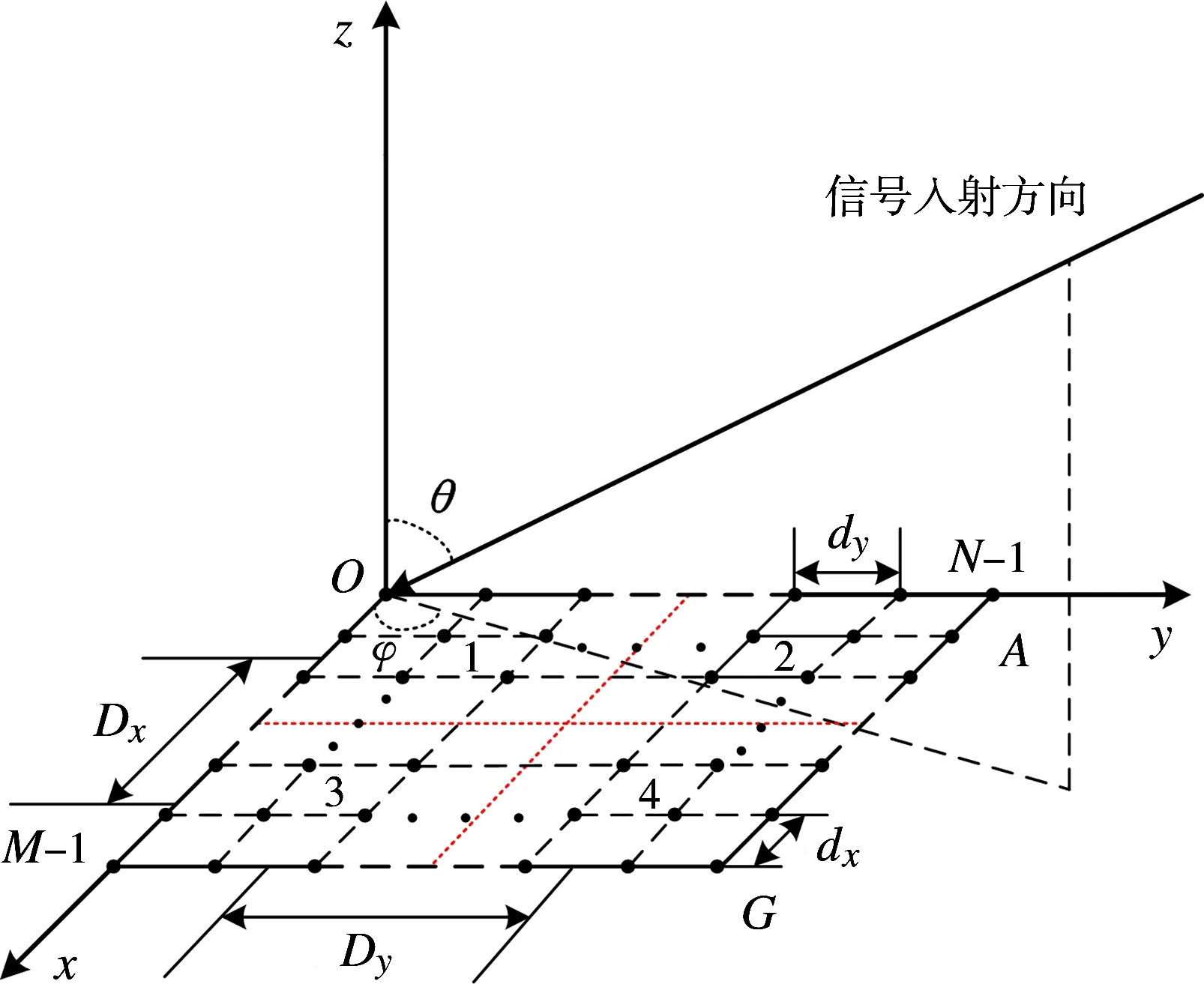
图5 矩形均匀面阵阵列几何结构

以坐标原点作为参考点，入射信号的导向矢量可以表示为

a(θ,φ)=[1e-jφ0×1(θ,φ)e-jφ0×2(θ,φ)…

e-jφ0×(N-1)(θ,φ)e-jφ1×1(θ,φ)…e-jφ(M-1)×(N-1)(θ,φ)]T

(3)

将导向矢量按照4个子阵进行划分，且每个子阵的阵元数为m×n，则4个子阵的导向矢量可以表示为a1，a2，a3，a4，存在如下关系[3]：

a1(θ,φ)=[1e-jφ0×1(θ,φ)e-jφ0×2(θ,φ)…

e-jφ0×(n-1)(θ,φ)e-jφ1×1(θ,φ)…e-jφ(m-1)×(n-1)(θ,φ)]T

(4)

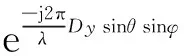
(5)

(6)

(7)

通常载波不含有用信息，阵列信号处理通常只考虑复基带。阵列接收信号的离散时间复基带信号可表示为

xi(n)=ai(θ,φ)s(n)+v(n)，i=1,2,3,4

(8)

设相控阵天线波束指向为(θ0,φ0)，则空域滤波器权向量w(θ0,φ0)可表示为

w(θ0,φ0)=[1e-jφ0×1(θ0,φ0)…e-jφ0×(N-1)(θ0,φ0)

e-jφ1×1(θ0,φ0)…e-jφ(M-1)×(N-1)(θ0,φ0)]T

(9)

同理，权向量按照子阵进行划分，可以表示为w1，w2，w3，w4。则空域滤波器输出可表示为

3 基带信号处理与实验结果

本节主要介绍基带信号处理部分。硬件实现时需要对信号作数字下变频处理，将信号变到基带，并产生复信号。基带信号处理包括搜索、角度估计和跟踪滤波三个过程。

3.1 互相关检测

运动平台设备获得的卫星位置预报信息和平台姿态的测量结果难免存在一定的误差，它使得自跟踪系统不能直接转入闭环跟踪状态，而须经过搜索阶段。

搜索过程包含两个状态，两个状态下的波位排列如图6所示。其中，状态1下的波位排列中心位置为载体平台给出的初始波束指向信息。首先，按照状态1的波位排列方式对每个波位内的信号进行能量检测，当能量大于某一门限值时，判定为成功检测到目标，否则，对下一波位进行能量检测。当状态1下的所有波位都没有检测到目标时，则按照状态2下的波位排列方式改变中心波位的位置，并重新按照状态1的波位排列方式对5个波位进行检测，直到检测出目标为止。

图6搜索过程波位排列方式

在接收信号信噪比较低的时候采用互相关方法进行检测[4]。某一波束指向下4个子阵输出信号与子阵1输出信号的相关系数为

(11)

将以上4个相关系数分别看作4个子阵输出信号的复幅度，合成后得到波束1,2,3,4,5的接收信号复幅度。i代表5个不同波束指向：

FΣi=R11+R12+R13+R14，i=1,2,3,4,5

(12)

以没有信号、只有噪声时的复幅度值作为门限，i代表4个不同子阵：

(13)

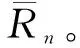
(14)

3.2 单脉冲比相测角

设子阵结构完全相同，第1子阵输出信号为y1(n)=z1(n)，是L个阵元的合成，即

(15)

且Δγ=γ0-γ，γ0是阵元波束指向的控制相位，γ是来波的实际空间相位。则其他各子阵输出为

y2(n)=z1(n)ejΔφ2，y3(n)=z1(n)ejΔφ3

y4(n)=z1(n)ejΔφ4

(16)

因为

(17)

y12(n)=y1(n)+y2(n)=

z1(n)(1+ejΔφ2)

(18)

y34(n)=y3(n)+y4(n)=

z1(n)ejΔφ3(1+ejΔφ2)

(19)

求上述两子阵输出的互相关，有

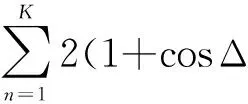
又因为

y13(n)=y1(n)+y3(n)=z1(n)(1+ejΔφ3)

y24(n)=y2(n)+y4(n)=z1(n)ejΔφ2(1+ejΔφ3)

(21)

求上述两子阵输出的互相关，有

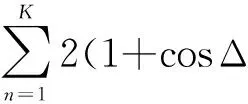
一般来说，上式中的噪声功率可忽略，此时分别求出Aφ3和Aφ2的相位，需注意，此时Aφ3和Aφ2的相位Δφ3与Δφ2之间的关系为

Δφ3=-∠Aφ3

Δφ2=-∠Aφ2

(23)

根据相控阵波束形成理论，Δφ2和Δφ3满足如下关系式：

(24)

(25)

式中，Dx，Dy为x方向和y方向子阵相位中心间距，λ为波长，θ，φ为信号入射角度，θ0，φ0为波束指向角度。将Δφ2，Δφ3代入式(24)和式(25)即可得

(26)

3.3 α-β跟踪滤波

卡尔曼滤波在雷达目标跟踪中有着丰富的应用[5]。在传统的卡尔曼滤波中，目标某个时刻的状态估计值为该时刻的预测值再加上一个与增益有关的修正项，而要得到增益矩阵，就必须计算一步预测自相关和新息过程自相关矩阵，增益矩阵的计算会占用大部分工作量。针对本文第2节提到的特定应用背景，采用α-β滤波器。α-β滤波器是一种针对匀速运动目标模型的常增益滤波器，增益矩阵可以离线计算，易于工程实现。

使用α-β滤波算法时，观测信息为目标入射角度[φ,θ]T，所以首先考虑用方向余弦作为状态向量。目标的方位和俯仰信息[φ,θ]T与之方向余弦信息之间存在着如下对应关系：

(27)

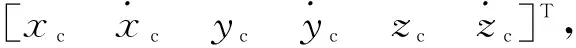
然后就可以应用α-β算法跟踪估计方向余弦的值，下面以一个通道的方向余弦估计为例进行说明，其余两个通道类似。

α-β滤波器是一种针对匀速运动目标模型的常增益滤波器，其中的增益矩阵具有如下形式：

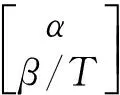
(28)

式中，α和β分别为目标状态的位置和速度分量的常滤波增益，T为采样周期。然后先定义机动指标λ为

(29)

式中，σ1和σ2分别为过程噪声和观测噪声的标准差。

α和β表达式如下：

(30)

(31)

下面为滤波具体步骤，离散化的目标运动状态方程为x(k)=F(k-1)x(k-1)+G(k-1)w(k-1)

(32)

观测方程为

z(k)=H(k)x(k)+v(k)

(33)

滤波步骤如下：

步骤1： 状态一步预测，即

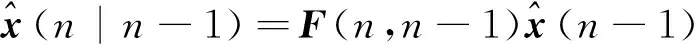
(34)

步骤2： 由观测信号z(n)计算新息过程，即

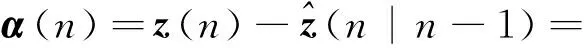
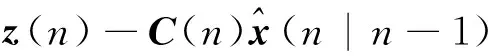
(35)

步骤3： 根据式(32)和式(33)计算滤波器增益。

步骤4： 状态估计，即

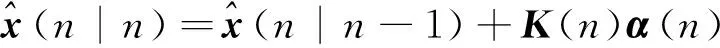
(36)

步骤5： 重复步骤1～4，进行递推滤波计算。

3.4 测试结果

首先将上位机、子阵信号发生器、基带信号处理单元分别通过对应的连接线连接好。在上位机初始界面上设置好目标运动的速度和加速度参数，设置初始波束指向偏离目标来波方向半个波束宽度，信噪比设为-10dB，观测时间为10s。点击上位机启动按钮后开始模拟自跟踪过程，上位机将角度估计误差和跟踪滤波误差数据进行保存成txt文件。最后将数据导入到Matlab后绘制误差曲线，观测误差和跟踪误差曲线如图7和图8所示。

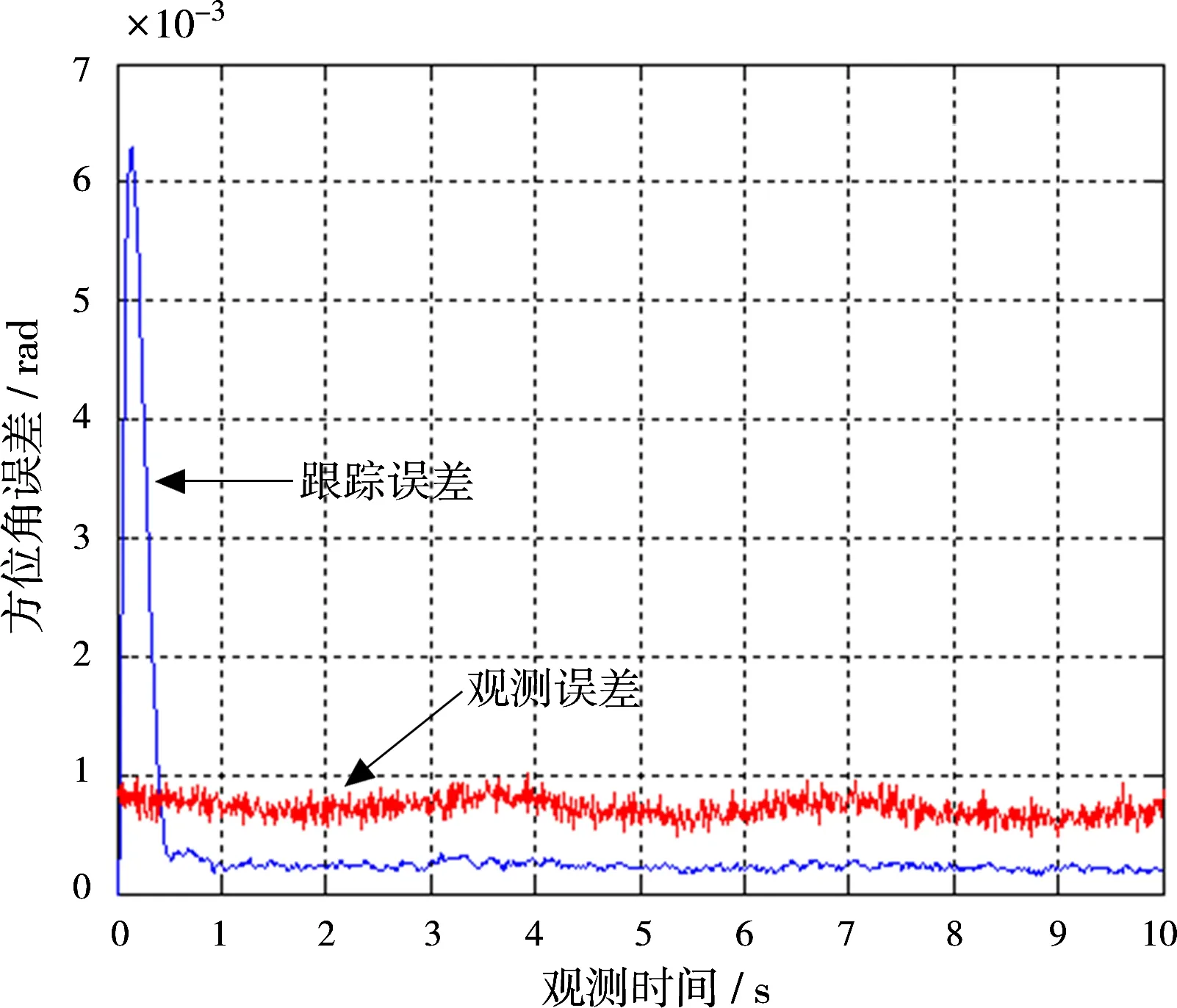
图7 存在随机噪声时方位角测角误差和跟踪误差曲线

为了更好地呈现测角精度和跟踪精度，上述曲线图舍去了开始时刻信号搜索过程中的角度误差部分。从上述实验结果可以看到，测角和跟踪曲线收敛后，测角精度小于0.5°，跟踪精度小于0.2°。测角精度会随目标姿态变化有一定的波动，经跟踪滤波后，误差曲线波动明显减小。

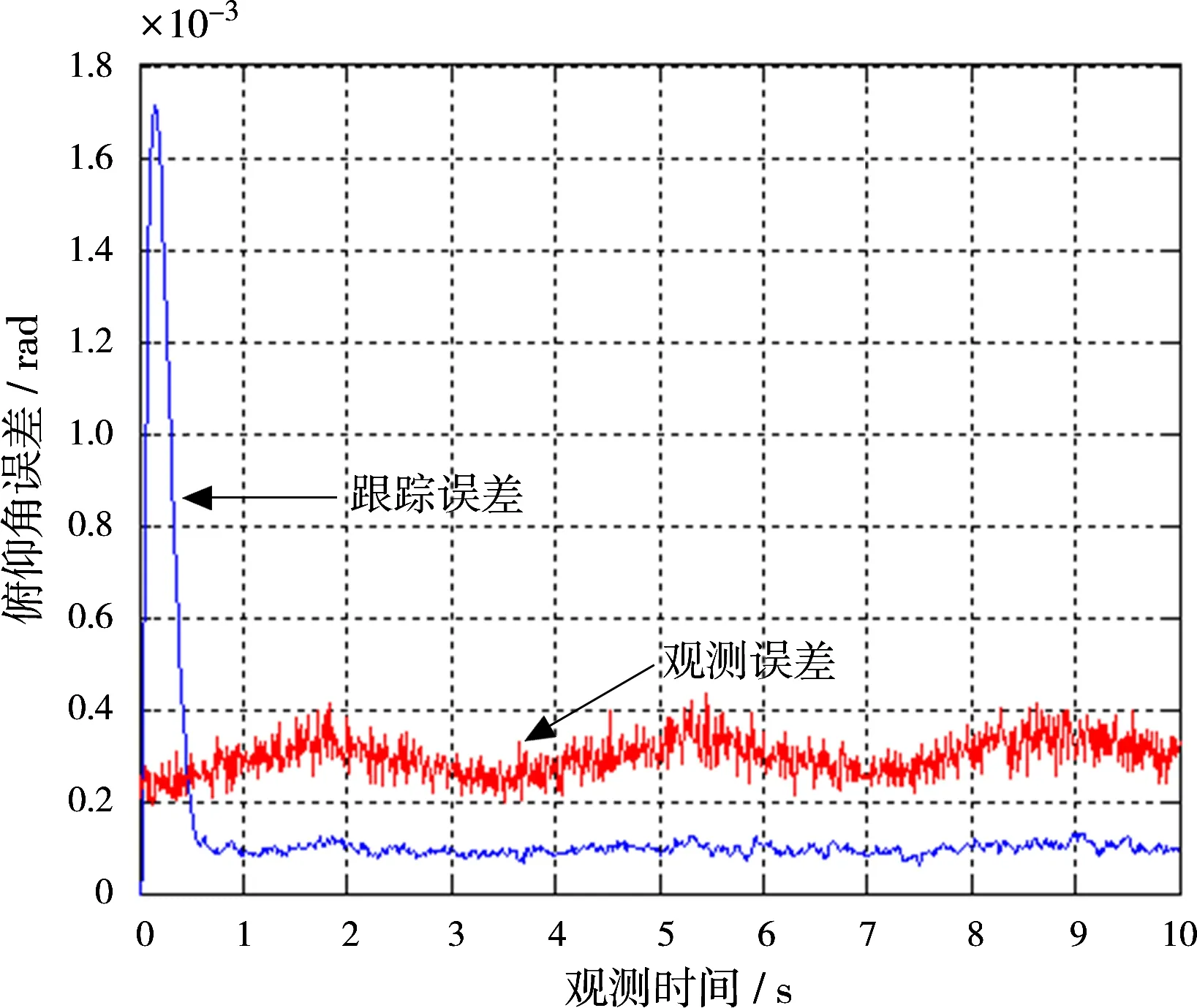
图8 存在随机噪声时俯仰角测角误差和跟踪误差曲线

4 结束语

本文针对相控阵卫星跟踪系统在实测时存在较高的测试难度和测试成本，设计了卫星跟踪闭环实验系统。系统通过上位机模拟了高速运动目标运动轨迹，借助FPGA硬件平台模拟产生相控阵天线接收信号，并将信号通过基带单元信号处理模块实现了卫星信号的搜索、角度估计和跟踪滤波，基带信号处理单元将跟踪滤波结果返还给上位机，从而不断调节波束指向，实现卫星跟踪闭环系统的演示。最后的实验结果证明了本系统设计的可行性和有效性，对工程实践具有指导意义。

[1]王洪伟. 便携式卫星通信地球站卫星跟踪技术的研究与实现[D]. 南京：南京邮电大学, 2013.

[2]张峰,田康生,息木林.弹道导弹运动建模与跟踪研究[J].弹箭与制导学报, 2012, 32(3):53-58.

ZHANG Feng, TIAN Kangsheng, XI Mulin. The Study on Ballistic Missile Modeling and Tracking[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(3):53-58.(in Chinese)

[3]何子述,夏威. 现代数字信号处理及其应用[M]. 北京：清华大学出版社, 2009.

[4]吕振肃,熊景松. 基于互相关和最大似然估计的弱信号检测[J]. 武汉科技大学学报, 2007, 30(4):398-400.

[5]张长春,黄英,杨刚. 卡尔曼滤波在跟踪运动目标中的应用及仿真[J]. 现代电子技术, 2009, 32(20):54-56.

[6]刘亮. 雷达测角方法研究[D]. 西安：西安电子科技大学, 2013.

[7]李鹏,武胜波. 比幅法测向及其误差分析[J]. 技术平台, 2009, 11(10):89-92.

[8]KALMAN R E, BUCY R S. New Results in Linear Filtering and Prediction Theory[J]. Journal of Basic Engineering, 1961, 83(1):95-107.

[9]刘延峰,潘泉,杜自成.机载雷达目标搜索和跟踪中的坐标系问题[J]. 火力与指挥控制, 2005, 30(3):40-43.