对称加载作用下单箱双室组合结构的剪滞效应特性与试验研究
喻江, 胡少伟, 卫聪杰, 张召广
(1.南京水利科学研究院 材料结构研究所,江苏 南京210024; 2.河海大学 水利水电学院,江苏 南京 210098;3.河海大学 土木与交通学院,江苏 南京 210098)
对称加载作用下单箱双室组合结构的剪滞效应特性与试验研究
喻江1,2, 胡少伟1, 卫聪杰1, 张召广3
(1.南京水利科学研究院 材料结构研究所,江苏 南京210024; 2.河海大学 水利水电学院,江苏 南京 210098;3.河海大学 土木与交通学院,江苏 南京 210098)
对于箱型组合结构,由于应力分布不均,极易导致翼板及底板发生剪切变形,从而对结构安全不利。为了深入探讨单箱双室组合结构中剪滞效应的机理,根据该类结构的受力变形特点,建立混凝土翼板和单箱双室钢梁的纵向翘曲位移模式,得到了控制微分方程及其边界条件,并推导出了在对称荷载作用下单箱双室组合结构的应变及挠度的解析表达式。开展了室内足尺寸模型试验,与剪滞效应理论进行了对比研究,应变、挠度计算值的最大相对误差分别达到15.32%和16.97%。可为该类结构中剪滞效应研究及单箱双室组合结构的工程设计、后期加固提供一定的参考。
单箱双室组合结构;剪滞效应;对称加载;试验研究;对比分析
我国现代化建设步入高峰,诸多已建或在建工程表明,钢-混凝土组合结构以其优良的结构形式、优越的受力性能被工程界大量采用,并取得了显著的经济效益和社会效益[1-2]。组合结构形式也由预制装配式组合梁、叠合板组合梁、钢板夹心组合梁等逐步走向多样化,其钢梁截面由最初的T型、I型向单箱型、单箱双室型、多箱型发展,混凝土翼板逐渐变高、变宽,跨度也逐渐变大[3-6]。在这类箱型结构中,其剪力传递不均,极易导致结构内纵向应力分布不均,超出正常使用状态,对其正常服役构成威胁。
对于组合结构剪滞效应问题的研究,可追溯到20世纪80年代,Asekola[7]最先对I型组合梁进行了剪滞效应分析。我国对组合梁中剪滞效应的研究起步较晚,程海根等[8]根据组合翼板微元的变形协调和平衡条件,得到了简支单箱组合梁用级数表示的应力解,并对剪滞效应进行了分析。吴文清等[9]对波形钢腹板单箱组合梁进行了剪滞效应分析。张阳等[10]通过试验和理论研究对大悬臂组合脊骨梁进行了剪滞效应分析。张彦玲等[11]对单箱组合梁进行了剪滞效应研究,并将理论解析解与试验结果及ANSYS软件的计算结果进行了相互验证。李平等[12]通过对大比例单箱组合梁进行加载试验研究,分析了组合箱梁在弹性受力状态下的剪滞效应特点。李运生等[13]考虑混凝土开裂的影响,对钢-混凝土连续组合梁的剪滞效应进行了研究。李法雄等[14]通过建立考虑界面滑移和翼板剪滞效应的双重效应模型,对在均布荷载和端部集中荷载作用下的简支组合梁进行了剪滞效应研究。胡邦瑜等[15]运用势能变分原理,得到了考虑剪滞效应的钢-混凝土组合梁的位移解析表达式。周勇超等[16]对I型组合梁进行了界面滑移与剪滞效应耦合效应分析。胡少伟等[17]对宽翼缘组合梁结构进行了剪滞效应计算分析与试验对比研究。易建强[18]对变截面波形钢腹板组合箱梁进行了剪滞效应研究。王连广等[19]通过假定一系列形函数对单箱组合梁进行了剪滞效应研究。文献[20-22]通过理论推导、试验研究等方法对双箱组合梁进行了剪滞效应研究。晏继伟等[23]考虑接触面滑移和翼板剪滞效应,导出了简支组合箱梁在均布力与集中力作用下的剪滞效应解析解,并加以研究。
国内外学者对组合结构剪滞效应的研究中,对单箱双室组合结构中剪滞效应的研究甚少。为了深入分析剪滞效应对单箱双室组合结构的作用机理和对结构造成的影响,本文通过建立单箱双室组合梁剪滞效应模型,导出了其考虑剪滞效应的控制微分方程,求得了在对称加载作用下应变和挠度的解析表达式,并结合试验算例,进行了对比研究。
1 控制方程的确定
1.1 建立条件
单箱双室组合结构由单箱双室钢梁和混凝土翼板组成。在分析考虑剪滞效应的组合结构的变形特征时,考虑如下基本假定:①按照等效截面法换算成等效截面进行分析;②不考虑双室钢梁与混凝土翼板相对滑移的影响;③混凝土翼板与钢梁的挠屈位移相等;④受力过程中混凝土和钢材均满足线弹性假定。
该类单箱双室组合结构的分析模型如图1所示。混凝土翼板的宽度为Bc,高度为Hc,形心为Oo。双室钢梁的宽度为Bs,高度为Hs,形心为Os。组合结构模型的形心为O。

图1 单箱双室组合结构分析模型
引入符拉索夫提出的广义坐标法理论[24-25],将该类组合结构的翘曲变形分解为竖向挠度u(z)与纵向位移w(x,y,z)。根据其几何对称特征和受力变形特征,假定双室钢梁底板纵向位移服从二次抛物线分布;混凝土翼板纵向变形分为两部分,与钢梁对应段服从二次抛物线分布,混凝土翼板外挑段服从三次抛物线分布;钢梁腹板仍然按照初等弯曲梁理论进行分析;钢梁托板由于较薄而且宽度相对很小,分析时可不考虑托板的影响。
单箱双室钢梁底板、混凝土翼板的轴向位移函数表达式分别为:

(1)
wc(x,y,z)=
(2)
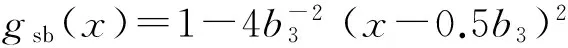

gc2(x)=1-(b2-b1)-3(b2-x)3。
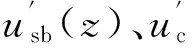
1.2 组合结构总势能
双室钢梁应变能Vs由两部分组成,包括钢梁底板应变能Vsb和钢梁腹板应变能Vsw。
Vs=Vsb+Vsw=

(3)

混凝土翼板应变能Vc的表达式为:

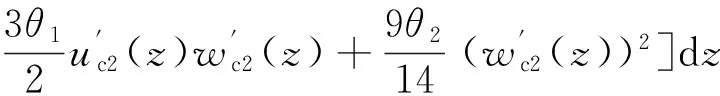
(4)
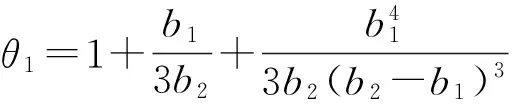



外力势能Vp表达式为:
(5)
式中M(z)为单箱双室组合结构在外荷载作用下的弯矩值。
组合结构总势能V的表达式如下:
V=Vs+Vc+Vp。
(6)
1.3 控制微分方程
根据基本假定③可得:
(7)
将式(7)进行一阶变分,得到该类组合结构考虑剪滞效应的控制方程:
(8)
式中:
k=(Jsb+1.5Jsw)Es+(Jc1+Jc2)Ec,
α1=k-1k1=JsbEs[(Jsb+1.5Jsw)Es+
(Jc1+Jc2)Ec]-1,
α2=k-1k2=(Jc1+1.125θ1Jc2)Ec[(Jsb+
1.5Jsw)Es+(Jc1+Jc2)Ec]-1,
β1=(8Jc1+9θ1Jc2)(112Jc1+135θ2Jc2)-1,
135θ2Jc2))-1。
2 应变及挠度的解析解
对式(8)消去u(z),并采用降阶法进行求解,于是得到双室钢梁和混凝土翼板的纵向位移及单箱双室组合结构的挠度。
(9)
式中

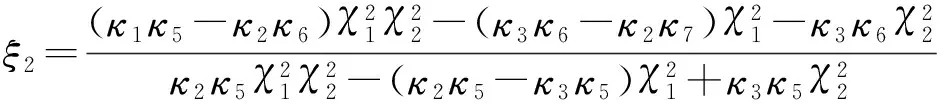


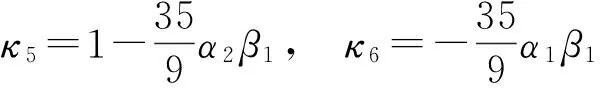


单箱双室组合结构的对称加载作用如图2所示。
因此,其剪力和弯矩的表达式可表示为:

(10)

(11)
简支单箱双室组合结构的边界条件和变分点的连续条件为:
(12)
将式(9)、(10)、(11)代入式(12),可得ws(z)和wc(z)的表达式,再代入式(1)和式(2),可得到考虑剪滞效应的单箱双室钢梁底板正应变的函数解析表达式:
(13)
ν=sh(χ1m)+sh(χ1(m+n)),
η=arth(χ1(m+n))+arth(χ1L),
τ=arsh(χ1m)arth(χ1(m+n))-νη,

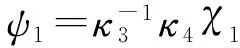
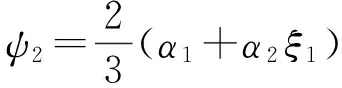
ψ3=τ-ch(χ1m),
ψ4=υarth(χ1L),

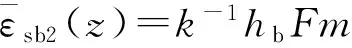
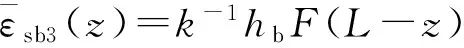

sh(χ1m)ch(χ1z)],
υch(χ1z)]。
同理,求得考虑剪滞效应的钢梁腹板正应变的函数表达式:
(14)
式中:ysw为钢梁底板形心到组合结构形心的距离,ysw∈(hb-hw,hb)。
因此,当0≤x≤b1时,考虑剪滞效应的混凝土翼板正应变的解析表达式为:
(15)
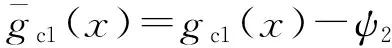




sh(χ1m)ch(χ1z)],
υch(χ1z)]。
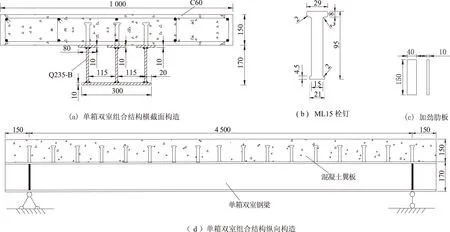
当b1 (16) sh(χ1m)ch(χ1z)], υch(χ1z)]。 根据简支组合结构在对称加载作用下的受力变形特点,组合梁结构的最大挠度发生在加载点之间某处。于是,解得考虑剪滞效应的单箱双室组合结构最大挠度的解析表达式为: (17) 3.1 试验概况 为了深入探究剪滞效应对单箱双室组合结构的具体影响,本次试验设计了1根足尺寸模型试件,编号为SBTCCS1。试件所选用的混凝土采用商品高强混凝土,强度等级为C60。钢梁选用Q235-B板材。混凝土翼板和单箱双室钢梁之间的连接通过在 钢梁上均匀布置帽型圆柱栓钉来实现。栓钉规格为15 mm×95 mm(直径×长度),采用3排分布,分别布置于3个钢梁托板上。根据栓钉布置原则,采用完全剪力连接形式。在受力过程中,支座处钢板易出现应力集中。为了消除该影响,分别在两个支座截面处设置加劲肋板[26-28]。模型梁尺寸及构造细节如图3所示。 图3 单箱双室组合结构模型试件(单位:mm) 3.2 测点布置 为了探究剪滞效应对该类组合结构的混凝土翼板、钢梁底板及腹板上应力、应变的影响,选择在组合梁跨中位置各截面处布置电阻应变片来探测其应变的变化情况,通过应变变化进一步探究应力的变化情况。电阻应变片的布置如图4和图5所示。为了探测模型梁在对称加载作用下荷载与挠度的变化关系,分别在钢梁底板的3个部位(1/2跨、1/3跨、1/6跨)布置位移计。 图4 混凝土顶面应变片布置(单位:mm) 图5 钢梁应变片布置(单位:mm) 3.3 加载及数据采集 试验加载系统采用液压伺服油压机结合配套的伺服液压计算机软件控制系统,并利用量程为0~1 000 kN的千斤顶对模型梁进行分级加载。试验加载过程通过计算机控制系统加以控制。初始加载频率控制在1次/5 min,加载20 kN。随着荷载值的变大,当钢梁接近屈服时,减小加载频率,控制在1次/10 min,加载10 kN,直到试件破坏为止。加载过程中,通过预先粘贴的应变片和荷载传感器测试被测点的应变及荷载。应变数据和挠度数据的采集,采用江苏华东测试技术有限公司开发的DH3816静态测试系统。荷载数据运用伺服液压计算机控制系统进行读数、记录。 4.1 应变分布特征 基于导出的考虑剪滞效应的单箱双室组合结构应变计算公式,在对称加载作用下,考虑不同弯矩(0.1My、0.3My、0.5My、0.7My、0.9My、1.0My,My=247.50 kN·m),求得钢梁底板跨中截面、钢梁腹板跨中截面、混凝土翼板跨中截面各位置处正应变沿截面横向的分布情况。 1)钢梁底板跨中截面的应变分布特征如图6所示。 图6 钢梁底板跨中截面的应变特征 图6(a)为应变的试验值与剪滞效应计算值的对比分析。可以看出:加载初期,应变沿横向分布较均匀,出现轻微的剪滞效应现象;随着荷载的不断增加,剪滞效应现象越加显著。图6(b)为应变计算值的相对误差分析。可以看出,不同测点处误差不同,94.45%数据相对误差在15.32%以内。 2)钢梁腹板的应变分布特征如图7所示。 图7 钢梁腹板跨中截面的应变特征 图7(a)中反映了钢梁腹板的应变沿梁高度方向的分布特性。对比分析表明,剪滞效应对钢梁腹板具有一定的影响。加载初期,其影响程度较小;随着荷载的不断增大,钢梁挠度的增加,其影响也变得更加明显。图7(b)为应变计算值的相对误差分析,95.83%数据的相对误差在15.19%范围内。 3)混凝土翼板顶面跨中位置的应变分布特征如图8所示。 图8 混凝土翼板顶面跨中截面的应变特征 从图8(a)可以看出,剪滞效应对混凝土翼板的影响显著。加载初期,剪滞效应影响不是十分明显;伴随着荷载的加大,其影响逐渐体现,当加载到1.0My时,影响最为显著。由图8(b)可知,通过比较,应变计算的相对误差在13.98%以内。 4.2 挠度变形特征 单箱双室组合结构在对称加载作用下挠度随荷载的变化情况如图9所示。 图9 挠度分布特征 由图9可知,考虑剪滞效应后,组合梁的刚度有所降低,使得挠度增大。试验采集到的最大挠度为94.36 mm,计算最大挠度为102.64 mm,计算值比实际值增大了8.28 mm。91.67%数据的相对误差在16.97%以内。 本文分析了在对称加载作用下,不考虑混凝土翼板和钢梁之间的滑移,和在材料线性的条件下,单箱双室组合结构的应变、挠度特性。 1)建立了一种研究单箱双室组合梁结构剪滞效应的分析模型,基于变分原理,求得在对称荷载作用下的应变、挠度函数表达式。进一步开展了室内足尺寸试验研究,与该种组合梁结构剪滞效应理论进行了对比分析。 2)选取典型截面(跨中截面),与导出的剪滞效应理论进行了应变、挠度对比。具体研究了钢梁底板及腹板跨中截面的应变分布特性、混凝土翼板截面的应变特性以及该种组合结构考虑剪滞效应后的挠度变形特征。对比分析表明,计算的变形相对误差在16.97%以内。 3)试验测试结果普遍小于剪滞效应理论计算结果。其影响因素为:①试验过程中翼板部分开裂导致其应变、挠度发生波动;②剪滞效应理论分析没有考虑滑移的影响。 [1]聂建国,余志武.钢-混凝土组合梁在我国的研究及应用[J].土木工程学报,1999,32(2):3-8. [2]胡少伟.钢-混凝土组合结构[M].郑州:黄河水利出版社,2005:15-22. [3]聂建国.钢-混凝土组合梁结构:试验、理论与应用[M].北京:科学出版社,2005:11-15. [4]胡少伟.组合梁抗扭分析与设计[M].北京:人民交通出版社,2005:34-43. [5]严国敏.现代斜拉桥[M].成都:西南交通大学出版社,1996:5-12. [6]范立础.预应力混凝土连续梁桥[M].北京:人民交通出版社,1999:13-18. [7]ASEKOLA A O.The dependence of shear-lag on partial interaction in composite beams[J].International Journal of Solids and Structures,1974,10(4):389-400. [8]程海根,强士中.钢-混凝土组合简支箱梁剪滞效应分析[J].西南交通大学学报,2002,37(4):362-366. [9]吴文清,万水,叶见曙,等.波形钢腹板组合箱梁剪滞效应的空间有限元分析[J].土木工程学报,2004,37(9):31-36. [10]张阳,邵旭东,王皓磊,等.大悬臂钢-混凝土组合脊骨梁的剪滞效应[J].中国公路学报,2008,21(3):57-63. [11]张彦玲,李运生,季文玉.简支组合箱梁在横向对称荷载作用下的解析解及剪滞效应研究[J].石家庄铁道学院学报(自然科学版),2009,22(1):5-14. [12]李平,刘凡,力为为.钢-混凝土组合箱梁弹性阶段剪滞效应的研究[J].苏州科技学院学报(工程技术版), 2009,22(2):21-24. [13]李运生,张彦玲,樊健生.考虑混凝土开裂影响的钢-混凝土连续组合梁剪滞效应研究[J].建筑结构学报,2010,31(增刊1):390-397. [14]李法雄,聂建国.钢-混凝土组合梁剪滞效应弹性解析解[J].工程力学,2011,28(9):1-8. [15]胡邦瑜,何云勇,陈勉.一种钢-混凝土结合梁剪滞效应的位移解析[J].四川建筑,2012,32(2):129-131. [16]周勇超,李常乐,孙铁军,等.钢-混凝土组合梁界面滑移与剪滞效应耦合效应分析[J].建筑科学与工程学报,2013,30(2):114-120. [17]胡少伟,喻江,谢建锋.宽翼缘组合梁结构剪滞效应计算分析与试验研究[J].应用数学和力学,2014,35(4):432-443. [18]易建强.变截面波形钢腹板组合箱梁剪滞效应的研究[D].兰州:兰州交通大学,2014:12-16. [19]王连广,万江.钢与混凝土组合箱梁剪滞效应分析[J].东北大学学报(自然科学版),2015,36(8):1204-1216. [20]胡少伟,喻江,张文敬.集中荷载作用下宽翼缘双箱组合梁剪滞效应分析[J].工程力学,2015,32(5):120-130. [21]胡少伟,喻江,谢建锋,等.预应力组合梁结构试验研究与剪滞效应分析[J].重庆交通大学学报(自然科学版),2015,34(4):7-14. [22]喻江,胡少伟.双室组合箱梁剪滞效应分析的偏泛函微分方法[J].应用数学和力学,2016,37(8):804-819. [23]晏继伟,蔺鹏臻.简支组合箱梁滑移效应及剪滞效应分析[J].兰州工业学院学报,2016,23(1):31-38. [24]DEZI L,GARA F,LEONI G,et al.Time-dependent analysis of shear-lag effect in composite beams[J].Journal of Engineering Mechanics,2001,127(1):71-79. [25]包世华,周坚.薄壁杆件结构力学[M].北京:中国建筑工业出版社,2006:382-388. [26]胡少伟,叶祥飞.部分剪力连接预应力组合箱梁受弯性能试验研究[J].建筑结构学报,2011,32(10):153-158. [27]胡少伟,赵克宇,喻江.复合弯扭作用下预应力单箱组合梁的扭转承载能力分析[J].华北水利水电大学学报(自然科学版),2015,36(2):1-6. [28]胡少伟,胡汉林.预应力钢-混凝土组合箱梁抗弯试验研究[J].建筑结构,2013,43(6):58-63. (责任编辑:陈海涛) Shear Lag Characteristics and Experimental Study for Simple-box Twin-cell Composite Structure under Symmetrical Loadings YU Jiang1,2, HU Shaowei1, WEI Congjie1, ZHANG Zhaoguang3 (1.Department of Materials and Structural Engineering, Nanjing Hydraulic Research Institute, Nanjing 210024, China;2.College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China;3.College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China) Due to the uneven distribution on stress for composite box structures, it is easy to cause shearing distortions on wing-plate and bottom-plate, thus exert negative impact upon structures. In order to in-depth discuss the shear lag mechanism of the simple-box twin-cell composite structure, a longitudinal warping displacement model is established according to its mechanical property and deformation feature, and its control differential equations and boundary conditions are also obtained. What′s more, special solution expressions of strain and deflection for this type of structure are deduced under symmetrical loadings in this paper. By conducting full-scale model test, a comparative analysis with the shear lag theory is launched. The results show that the maximum relative errorson calculated values of strain and deflection are 15.32% and 16.97%, respectively. Finally, this kind of analysis method can provideguidance for composite structure engineering design and late reinforcement. simple-box twin-cell composite structure; shear lag effect; symmetrical loadings; experimental research; compared analysis 2016-07-11 国家杰出青年科学基金(51325904);国家自然科学基金(51279111)。 喻江(1989—),男,重庆云阳人,博士研究生,从事组合结构方面的研究。E-mail:yzyzyz322@126.com。 胡少伟(1969—),男,河南杞县人,教授级高级工程师,博导,从事水工结构工程与材料方面的研究。E-mail:hushaowei@nhri.cn。 10.3969/j.issn.1002-5634.2017.01.011 TV222;TU398+.9 A 1002-5634(2017)01-0052-08


3 足尺寸模型试验

4 结果对比分析



5 结语

