基于水质响应系数的浅水湖泊水环境容量计算方法

张 茜，韩龙喜

(河海大学环境学院，南京 210098)

·水环境·

基于水质响应系数的浅水湖泊水环境容量计算方法

张 茜，韩龙喜

(河海大学环境学院，南京 210098)

根据湖泊污染物迁移转化机理、质量守恒原理，提出浅水湖泊污染物浓度场稳定判别方法。根据湖泊浓度场稳定后水质控制点污染物浓度与各入湖河道污染物通量的响应关系，构建多入湖河流水质响应系数矩阵，并采用线性规划法求解浅水湖泊各入湖河道水环境容量。与常规方法相比，该方法充分考虑了多入湖河流入湖污染物通量的叠加影响，提高了湖泊水环境容量的计算精度。

水环境容量；水质响应系数；线性规划。

1 前 言

中国是一个多湖泊国家，大于1km2的湖泊有2 300多个，湖泊和水库总贮水量可达6.380×1011m3。湖泊是内陆水体供水的主体，全国城镇饮用水源的50%以上来源于湖泊[1]。近几十年，随着湖泊周围地区人口增加和经济高速发展，入湖污染物急剧增加导致湖泊水环境质量不断恶化，引起了许多水环境问题，如湖泊富营养化灾害频频发生，湖泊生态系统不断退化等，某些地区由于严重的水质性缺水制约了经济的可持续发展。

水环境容量指在不影响水的正常用途的情况下，水体所能容纳的污染物的量或自身调节净化并保持生态平衡的能力。确定水体环境容量对于控制污染物排放总量，最大程度地利用水体的自净能力进行水环境规划，合理的利用水资源具有重要意义。目前我国许多学者对湖泊水环境容量计算方法进行了深入的研究：文献[2～6]采用完全混合湖泊非保守污染水质模型计算湖泊水环境容量，但污染物进入湖泊后的迁移转化非常复杂，并不能达到完全混合状态；文献[7～14]采用二维非稳态水量水质数学模型，根据河道设计水量及相应功能区水质目标值计算得到不同风向下形成污染带的允许排污量即为湖泊的水环境容量，只考虑了各个排污口单独的影响并进行简单的叠加，并未考虑各个排污口之间相互的叠加影响；文献[15-16]通过水流水质模型求得各排污口在单位负荷下的响应场，建立排污口负荷与控制点之间的相应关系，应用线性规划法计算得到博斯腾湖的环境容量，但在计算环境容量时重复考虑了背景浓度值，导致计算的结果并不是真正意义上的水环境容量。这些文献都为湖泊水环境容量的计算提供了很好的研究方法，但均未充分考虑污染物进入湖泊后的实际迁移扩散过程以及每条入湖河流与控制点之间的污染物浓度响应关系。

本文在前人研究的基础上提出一种利用水质响应系数计算湖泊水环境容量的方法，即在湖泊风生环流的作用下，每条入湖河流对不同控制点的浓度场具有不同的累积叠加影响，控制点处的污染物浓度首先呈现上升趋势最终达到稳定状态，同时根据湖泊水量平衡原理和水体的自净能力，当入湖污染物通量、出湖污染物通量与湖体自净量处于动态平衡时，可以认为湖泊整体水质情况达到相对稳定状态，在此稳定状态基础上利用水质响应系数计算湖泊的水环境容量既充分考虑了水体的自净能力又考虑了各个入湖河流与控制点之间的污染物浓度响应关系，由此计算得到的湖泊水环境容量更能与实际情况相符，具有更高的精确度。

2 水质响应模型的建立

2.1 水质响应系数

水质响应系数即污染物进入湖体后，随湖体风生环流迁移扩散，各个入湖河流对不同控制点的浓度场具有不同的累积叠加影响，水质响应系数反映了各个入湖河流对湖泊内各点浓度场的贡献值，可根据控制点处的水质响应系数推求各个入湖河流的最大允许入流浓度，以此求得湖泊水环境容量。

2.2 二维水动力-水质响应模型

基本控制方程

二维非恒定浅水方程组为：

(1)

(2)

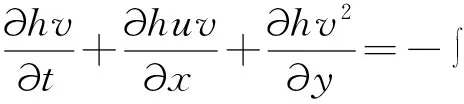
(3)

(4)

式中：t为时间；x，y为笛卡尔坐标系坐标；η为水位；d为静止水深；h=η+d为总水深；u，v分别为x，y方向上的速度分量；ʃ是哥氏力系数ʃ=2ωstnφ，ω为地球自转角速度；φ为当地纬度；ρ为水的密度；sxx、sxy、syy分别为辐射应力分量；S为源项；(us,us)为源项水流流速；Txx、Txy、Tyy为水平黏滞应力；Txx、Tsy为表面风应力；Thx、Thy为底摩擦应力；c为污染物浓度，mg/L；Ex、Ey为x，y方向的紊动扩散系数和分散系数之和；k为衰减系数。

长荡湖平均水深1.5m，湖底地形平坦起伏不大，常年主导风向为西南风，将所有与其连通河流概化为9条入湖河流与5条出湖河流，河流位置如图1所示，其中新建河、涑渎河、新河港、大浦港、白石港、仁河港、清水渎港、庄阳港和北河为入湖河流，河下河、中干河、儒林中河、北干河和湟里河为出湖河流。在湖中取五个点作为控制点，控制点处水功能区划为Ⅲ类，根据污染带控制确定控制点的位置，参考中国环境规划院编制的《关于对全国地表水环境容量核定有关问题的进一步说明》，“大型湖泊岸边污染带范围控制在1～3km2为宜”。本文选取污染带控制范围为1km2，根据浓度包络线分布形状确定污染带具体范围，选定的控制点位置见图1。

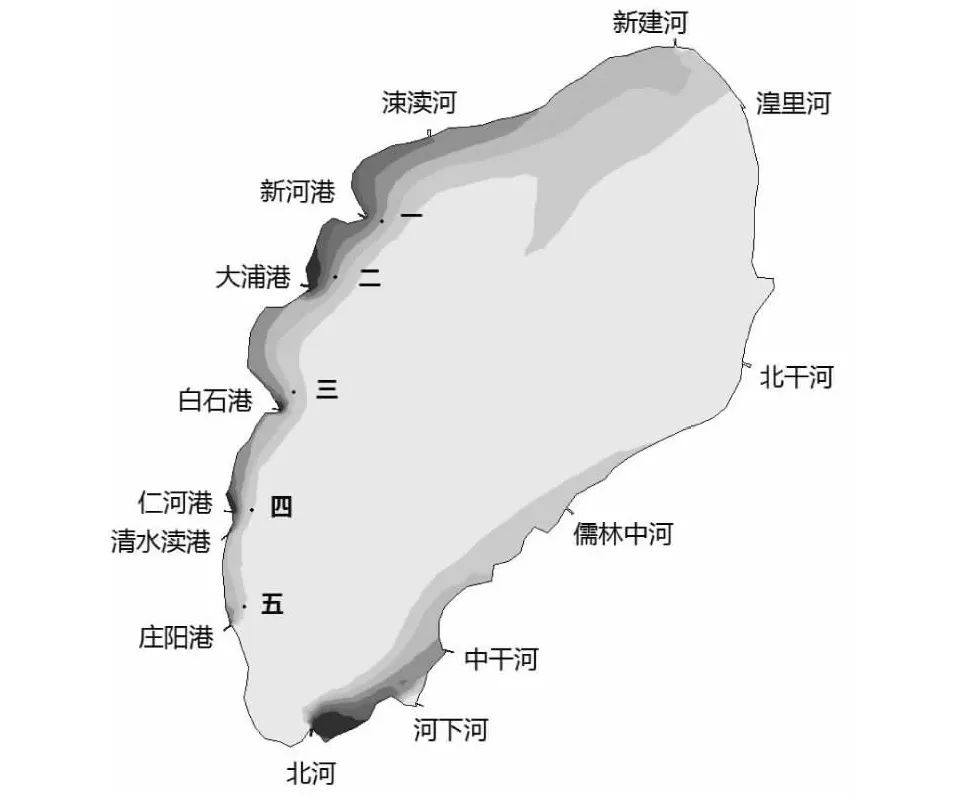
图1 浓度场与控制点位置图Fig.1 Concentration field and control point locations

2.3 湖泊风生环流

一般认为，绝大多数大型浅水湖泊水深不超过20m，不会出现密度分层现象[8]，且湖泊常年受闸控，入湖出湖流量变化相对较小，故湖流的成因类型主要属于风生流，同时湖泊也容易到达相对稳定的状态。

边界条件：通过对长荡湖水文资料的收集整理，选取最不利设计水情(90%频率湖泊水位和90%频率入湖河流流量)，共设14个断面，其中9个入流断面，5个出流断面，具体断面情况见表1。

通过模型模拟得到如图2风生环流流场：在常年主导风向西南风作用下，湖泊西部和东部分别形成一个顺时针和逆时针方向的环流，中部湖流由东北向西南。

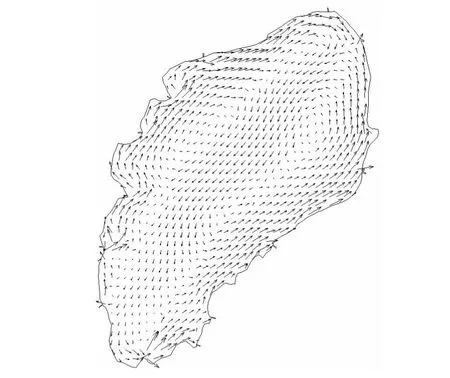
图2 西南风(SW)作用下风生环流流场Fig.2 Wind-driven flow field by southwest wind

河 流边界条件类型断面流量或水位编号新建河流量3.00m3/s1涑渎河流量0.54m3/s2新河港流量1.71m3/s3大浦港流量8.20m3/s4白石港流量3.01m3/s5仁河港流量1.98m3/s6清水渎港流量1.85m3/s7庄阳港流量2.00m3/s8北河流量8.00m3/s9河下河水位1.5m10中干河水位1.5m11儒林中河水位1.5m12北干河水位1.5m13湟里河水位1.5m14

3 湖泊水质变化过程

3.1 湖泊整体浓度场分布

边界3～9假定入湖COD浓度为1mg/L，COD综合降解系数0.01mg/d。模拟时长足够长，五个控制点处COD浓度变化过程见图3。

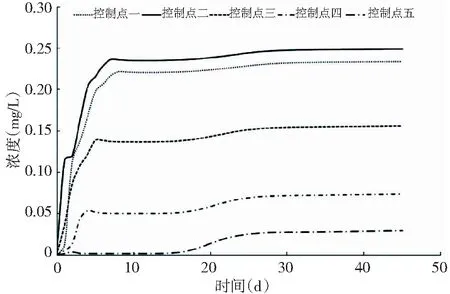
图3 控制点处COD浓度变化过程Fig.3 The changing process of COD concentration at control points

假设湖泊中初始污染物COD浓度为0，污染物进入湖体后首先被稀释，然后随湖流从高浓度到低浓度进行迁移扩散，同时一部分污染物被水体中的微生物降解，即湖泊的自净作用，在入湖流量和污染物入湖浓度恒定的情况下，五个控制点处污染物浓度场的变化都呈现出先呈现增长后浓度基本保持不变的趋势。在本文所研究湖泊给定的初始条件下，五个控制点处污染物浓度场在一个月后才慢慢的达到稳定，说明污染物进入湖体后经过相当长的一段时间后湖泊的整体水质才能达到稳定状态，湖泊水质达到稳定状态所需要的时间与湖泊的水动力特征及水生态环境等因素有关，此时的污染物浓度才是湖泊充分发挥其自净能力后能真正能代表湖泊水质的污染物浓度，此时湖泊内某监测点的污染物浓度才能作为计算水环境容量的依据。而前人所提出的计算水环境容量的方法并没有充分考虑湖泊水质稳定过程，故计算得到的水环境容量比实际的水环境容量偏保守。

3.2 控制点处污染物浓度累积叠加过程

边界1新建河与边界3新河港分别假定入湖COD浓度为1mg/L，其他入流边界COD浓度为0，新建河与新河港分别对控制点处浓度场的累积叠加过程见图4。

由图4中可知，即使控制点分散于湖泊不同位置，各个入湖河流对各个控制点处的浓度场依然会产生一定的累积叠加影响，且不同控制点对入湖河流的响应程度不同，直到湖泊到达稳定状态，各控制点处的污染物浓度基本不再变化。由于浅水湖泊受到风生环流影响较大这种特征，污染物进入湖泊后，其迁移扩散过程与污染物在河流中的迁移扩散过程完全不同，污染物会随着湖流迁移扩散到湖泊各个位置，即每条入湖河流对湖泊各处的浓度场都有一定的贡献值。

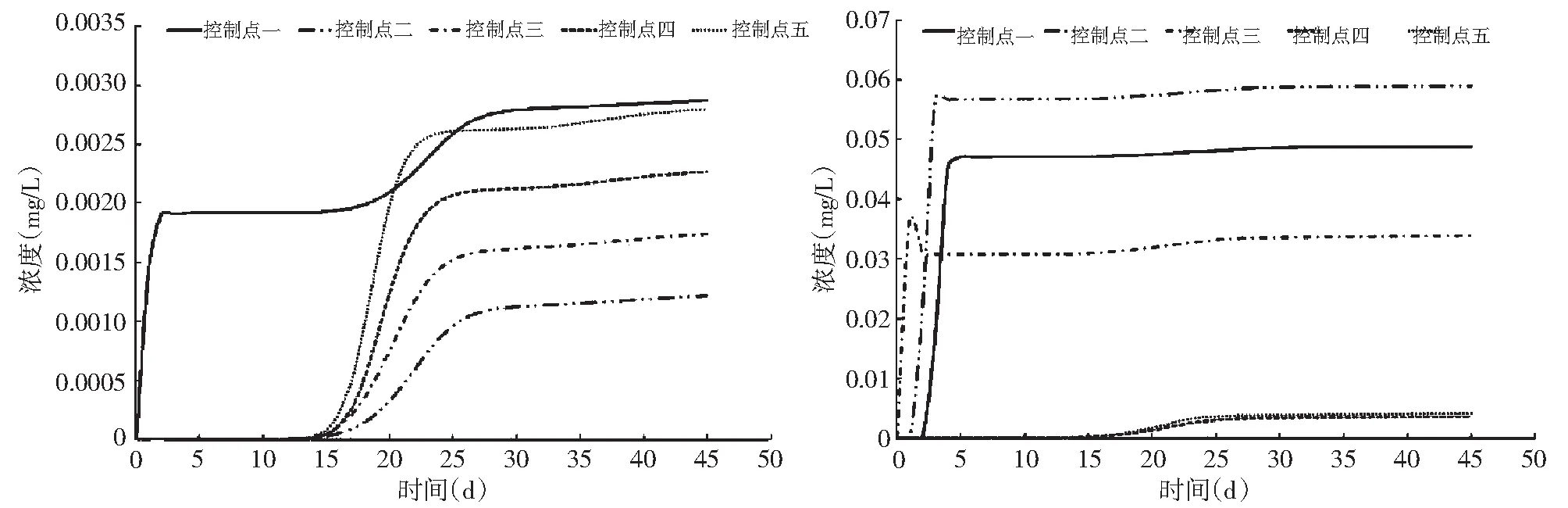
图4 新建河、新河港对各控制点处COD浓度贡献值Fig.4 COD concentration contribution of Xinjian River and Xinhegang in each control point

3.3 湖泊内污染物通量变化过程

通过水动力-水质响应模型模拟得到湖泊水质稳定后COD物质的量动态平衡见图5。

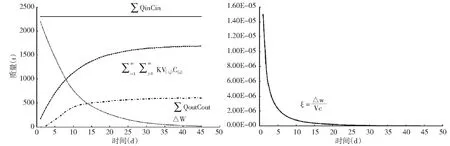
图5 COD质量守恒变化过程Fig.5 Conservation of mass changing process of COD

质量动态平衡公式：

W入湖通量=W自净量+W出湖通量+ΔW

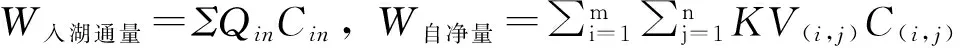
W出湖通量=ΣQoutCout

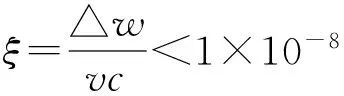
由于入湖流量和COD入湖浓度假定为定值，因此入湖通量保持不变，根据物质守恒原理，当湖泊达到稳定状态时入湖通量理论上应等于出湖通量与自净量之和，但由于外界其它因素的影响，这三者没办法达到绝对的平衡，为了保证物质守恒本文引入残差Δw这一概念。由图5中可知，大约40天后入湖COD通量基本等于出湖COD通量与COD自净量之和，此时湖内COD的增量几乎为0，可以认为在水量平衡与湖泊自净作用下，此时湖泊整体水质到达了稳定状态。

4 湖泊水环境容量计算方法

4.1 确定水质响应系数

式中：C为控制点处污染物浓度值；P为入湖河流污染物浓度值；m为控制点个数；α矩阵为浓度响应系数；n为入湖河流个数。

通过假设各入湖河流浓度，利用水动力-水质响应模型计算控制点处相应的浓度场求得浓度响应系数矩阵。

4.2 耦合线性规划法计算湖泊水环境容量

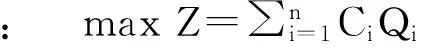
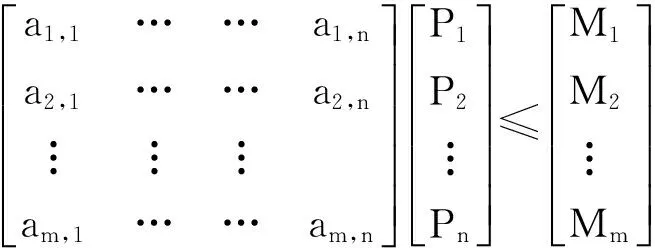
Pu≤P1,P2,P3…Pn

式中：α矩阵为浓度响应系数；M为控制点处水质标准；Q为入湖流量；P为入湖河流污染物浓度值；Pu为入湖河流最低浓度限值，具体浓度由当地水质目标决定；m为控制点个数；n为入湖河流个数。

4.3 水质响应模型在计算长荡湖水环境容量中的应用

在最不利设计水文条件(90%频率湖泊水位和90%频率入湖河流流量)下，经稳态判别公式判定湖泊到达了相对稳定状态，由水质响应系数矩阵计算得到各入湖河流对各控制点的单位水质响应系数，水质响应系数计算结果见表2，耦合线性规划法计算得到长荡湖水环境容量，水环境容量计算结果见表3。

在给定入湖河道位置、设计水量和水质目标等条件下，计算得到长荡湖COD最大允许入湖总量为22 784.77吨/年。

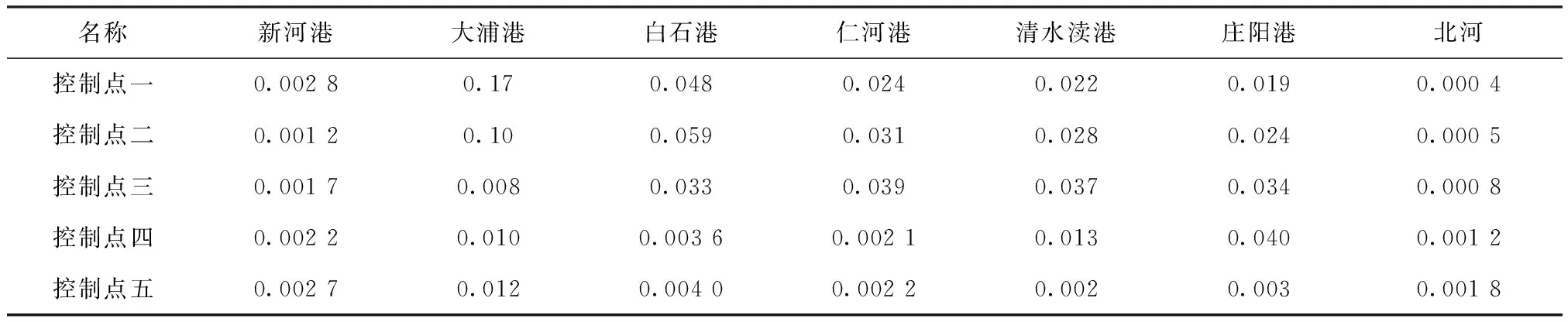
表2 各入湖河流对各控制点的水质响应系数Tab.2 Water quality response coefficient of each control point

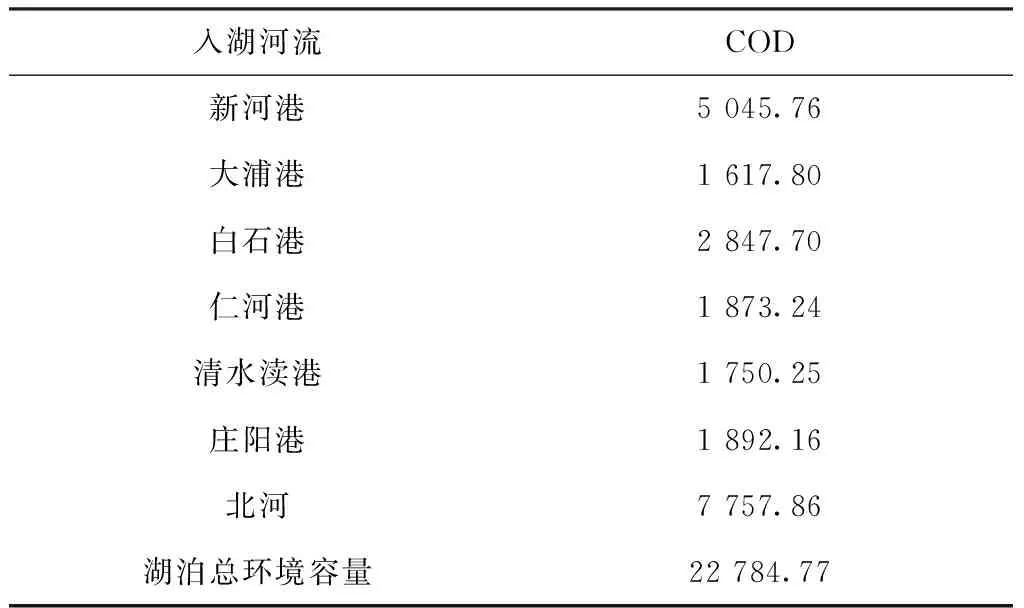
表3 长荡湖水环境容Tab.3 Water environment capacity ofChangdang Lake (t/a)

5 结 论

本文通过建立二维水动力-水质模型模拟长荡湖风生环流流场及污染物浓度场，证明了本文所提出的观点即污染物进入湖泊后，对湖泊各处的污染物浓度场产生累积叠加影响，而经过一段时间后湖泊整体水质随着水量平衡和水体自净作用达到稳定状态，提出了湖泊稳态判别公式，并建立了入湖河流与控制点处的污染物浓度响应关系，利用线性规划法求得长荡湖水环境容量，此方法具有很高的实用性与可操作性，可为基于污染物总量控制的环境规划提供科学依据。

[1] 吴丰昌, 孟 伟, 宋永会,等. 中国湖泊水环境基准的研究进展[J]. 环境科学学报, 2008, 28(12):2385-2393.

[2] 杨文龙, 杨常亮. 滇池水环境容量模型研究及容量计算结果[J]. 云南环境科学, 2002, 21(3):20-23.

[3] 王玉敏, 周孝德, 李家科. 湖泊水环境容量迭加计算方法研究[J]. 干旱区资源与环境, 2005, 19(6):108-112.

[4] 杨诗君, 李广源. 洞庭湖水环境质量评价及水环境容量分析[J]. 水文, 2006, 26(5):83-85.

[5] 李如忠, 洪天求. 盲数理论在湖泊水环境容量计算中的应用[J]. 水利学报, 2005, 36(7):765-771.

[6] 张利民, 刘 洋, 孙卫红,等. 太湖流域漕桥河小流域水环境容量估算及污染物削减分配[J]. 湖泊科学, 2009, 21(4):502-508.

[7] 范丽丽, 沙海飞, 逄 勇. 太湖湖体水环境容量计算[J]. 湖泊科学, 2012, 24(5):693-697.

[8] 胡开明, 逄 勇, 王 华. 大型浅水湖泊水环境容量计算研究[J]. 水力发电学报, 2011, 30(4):135-141.

[9] 孙卫红, 逄 勇, 姚国金. 基于不均匀系数的水环境容量计算方法探讨[J]. 水资源保护, 2001(2):25-26.

[10] 戴本林, 杨立中, 贺玉龙,等. 四川省茶坪河水环境容量及总量控制[J]. 湖泊科学, 2008, 20(1):39-44.

[11]YanB,XingJ,TanH,etal.AnalysisonWaterEnvironmentCapacityofthePoyangLake[J].ProcediaEnvironmentalSciences, 2011, 10:2754-2759.

[12]KangP,XuL.WaterEnvironmentalCarryingCapacityAssessmentofanIndustrialPark[J].ProcediaEnvironmentalSciences, 2012, 13(10):879-890.

[13]YangJ,LeiK,KhuS,etal.AssessmentofwaterenvironmentalcarryingcapacityforsustainabledevelopmentusingacoupledsystemdynamicsapproachappliedtotheTielingoftheLiaoRiverBasin,China[J].EnvironmentalEarthSciences, 2015, 73(9):5173-5183.

[14]WangH,ZhouY,TangY,etal.Fluctuationofthewaterenvironmentalcarryingcapacityinahugeriver-connectedlake.[J].InternationalJournalofEnvironmentalResearch&PublicHealth, 2015, 12(4):3564-3567.

[15] 刘 江, 贾尔恒·阿哈提, 程 艳. 水质响应模型与规划法耦合测算湖泊环境容量[J]. 中国农村水利水电, 2013(9):16-19.

[16] 刘晓波, 彭文启, 何国建,等. 基于水质-污染源响应关系的抚仙湖水环境承载力计算研究[J]. 水动力学研究与进展, 2011, 26(6):652-659.

A Water Environmental Capacity Calculation Method of the Shallow Lake Based on Water Quality Response Coefficient

ZHANG Xi，HAN Long-xi

(CollegeofEnvironment，HohaiUniversity，Nanjing210098，China)

According to the migration mechanism of lake pollutant and the principle of conservation of mass, concentration field stability discriminant method of pollutants in shallow lakes is put forward. According to the cumulative response relationship between pollutant concentration of control point and flux of inflow river into lake when the lake concentration field is stabilized, water quality response coefficient matrix of inflowing rivers is build, and used linear programming method to calculate the water environmental capacity of inflowing rivers. Compared with conventional methods, this method fully considers the superposition influence of pollutant flux of inflowing river and improved the calculation precision of the water environmental capacity.

Water environment capacity;water quality response coefficient;linear programming

2016-11-20

张 茜(1992-)，女，辽宁朝阳人，河海大学环境科学与工程专业2014级在读硕士研究生，主要从事水文学、流体力学及水环境规划研究。

X143

A

1001-3644(2017)01-0047-06