三垂线定理教学初探

文/钟瑜

一、如何教学三垂线定理

(一)研究背景

在数学教学的探讨这一方面，前人已经做了相当多的研究。绍兴师专学报刊登的《论数学方法的教学》、南京师范大学韩龙淑博士提出的《数学启发式教学研究》、东北师范大学刘先茹提出的《高中数学问题解决及其教学研究》、华东师范大学的吴骏博士提出的《基于数学史的统计概念的教学研究》等等。在教学的这个方面，学者们都下了不少的功夫，从各个层面去分析教学上的问题，以达到把我们的数学知识点在课堂上更加完美的呈现出来的目的。这样的研究也有力的推动了我国数学文化的发展。

三垂线定理及其逆定理是整个立体几何的一个典型代表，是立体几何的一个重要定理。①三垂线定理是立体几何知识的枢纽——三垂线定理在线面垂直的基础上来研究直线间垂直关系的重要定理，它阐明了平面的斜线、射影以及平面内的直线三者的垂直关系，沟通了线线关系、线面关系，为今后学习面面垂直，空间角、多面体与旋转体的性质等奠定基础。并且，三垂线定理及其逆定理因涉及的概念较多、在立体几何的证明中应用较广而成为立体几何的重点。②三垂线定理有利于培养学生的逻辑思维能力——三垂线定理及其逆定理是培养高中学生空间想象力和逻辑思维能力的重要内容之一。只要围绕三垂线定理合理进行解题变式的训练，将对学生的多种能力的培养有更加重要的、独到的作用。

当然，在三垂线定理的教学探讨上，很多学者也已对其进行了分析、解剖。他们分别对这个课题从讲解的角度进行一一分析，对学生能力的培养，突破三垂线定理的教学的难点方法，三垂线定理的利弊等各方面进行探讨。他们提出问题的同时也发表自己相应的观点，并且以与学生共同探讨的思想进行教学。目前在对教学探讨上的研究仍是以数学方法、部分数学问题为主要方面，已有的教学探讨对学生的学习情绪缺乏关注。本次笔者研究主要是基于前人的基础上，分析出教师、学生这两大因素给教学带来的影响，根据这些影响寻求到一个较好的解决方案。

(二)如何进行三垂线定理的讲解

三垂线定理及其逆定理本身来说并不是十分复杂的，但很多学生对定理的理解往往浮于表面。这就要求教师在教学的过程中应该注意以下几个方面：一是，要强化三垂线定理的条件。教师在教学过程中要仔细的向学生剖析出三垂线定理的内容中的条件，和学生一起探讨出三垂线定理中的条件与结论的含义。特别是要强调“平面内的一直线、这个平面的一条斜线、这条斜线在该平面内的射影”等一系列极其容易被忽视的条件；二是，教师应该在本堂课揭示三垂线定理及其逆定理的实质。三垂线定理及其逆定理都是研究线与线的垂直关系的，他们要揭示的实质都是：平面的一条斜线与该斜线在平面内的射影必然是同时垂直于该平面的某一条直线的。而这条斜线与其射影所垂直的那条平面的直线与斜线存在两种关系，要么相交，要么异面。无论他们是什么样的关系，教师只要抓住三垂线定理及其逆定理的实质，这样有助于学生更好的理解，把握三垂线定理及其逆定理的知识点；三是，应该理清三垂线定理的结构关系。教师在教学三垂线定理的过程中，学生学习定理的一大难点是一时分不清楚各条直线之间的关系，教师应该帮助学生理清楚我们本节课所要涉及的面与线，线与线之间的关系，在教学的过程中给定一个支架图，标明本节课所要涉及的面，线，让学生一目了然的观察出三垂线定理及其逆定理的条件与结论无非仅涉及了四线、三垂以及一平面，相信在这个环节，学生能清楚的了解到这四线分别是哪些，三垂是哪些线与线的垂直，面与线的垂直。在实际的学习中学生一定要先找到两个垂直，再推出第三个垂直，这样在以后的应用中就要容易许多。

在讲完以上三点之后，教者可以安排以下的几个问题，帮助学生明辨是非，消除对定理定义的模糊理解。

例题1下列命题是否正确，为什么？

(1)和平面斜线垂直的直线也和斜线在该平面内的射影垂直。

(2)直线a是平面α的斜线，直线b垂直于a在平面内的射影，则a⊥b.

(3)直线a是平面α的斜线，平面β内的直线b垂直于直线a在平面α上的射影，则a⊥b.

(4)直线a是平面α的斜线，平行于平面α的直线b垂直于直线a在该平面的射影，则a⊥b.

这四个命题中，仅有命题(4)是正确的，由这四个命题，我们进一步的强调了三垂线定理及其逆定理的相关条件和结论，而且，我们可以看出，三垂线定理及其逆定理的成立，都要求这四线是相对于同一个平面而言。

(三)正确区分三垂线定理及其逆定理

三垂线定理及其逆定理在理论上的叙述是极其的相似，因而，很多的学生在学习三垂线定理及其逆定理时很容易将它们的定义混淆，很多学生往往说不清楚谁是原定理，谁是逆定理，从而导致学生在知识的把握上感到头疼。对此，我们教师就应该设法讲清二者的区别，找到一种适合学生记忆的简单的鉴别方法。事实上，三垂线定理是判定平面内的一条直线与平面的一条斜线即平面外的一条直线的垂直关系，那么我们就可以简单记为判定平面“内、外”直线的垂直关系。而三垂线定理的逆定理是判定平面内的一条直线与平面的斜线在该平面内的射影的垂直关系，那么我们就可以简单的记为判定平面“内、内”直线的垂直关系。在蒋建华《优化三垂线定理教学之管见》中表明教学中将这两个简单的记忆方式引出来，便易将三垂线定理及其逆定理更好的区分开来，并且这样的教学方法使得教学效果显著。

(四)三垂线定理及其逆定理是爪子定理的特例

在高中数学中，三垂线定理及其逆定理是爪子定理的一个特列所在，那么什么是爪子定理呢，我们一起来看一下。

爪子定理：如下图所示，过平面α外一点O引一条斜线，交该平面于点A，过O点做平面α的垂线，交平面α于点B，连接直线AB，过点A做射线AC，AC在平面α上，所以有cos∠OAC=cos∠ BACcos∠ OAB， 当 ∠ BAC =90度，必有∠OAC =90度，此时为三垂线定理；当∠OAC =90度，必有∠BAC=90度，此时为三垂线定理的逆定理。中，自然而然的学会知识点的连线，总的来说，这一步的教学，有着重大意义。

(五)如何灵活应用三垂线定理及其逆定理

在高中数学的教学中，教师对三垂线定理及其逆定理的教学，主要是为了能让学生灵活的应用三垂线定理及其逆定理，使得学生在遇到实际的问题时能运用三垂线定理及其逆定理进行解决。很多同学在学习了三垂线定理之后，遇到问题总是绕道而行，不知如何应用，那么教师在教学的过程中，应该着重的引导学生，培养学生灵活应用定理的能力，强化利用定理解题的意识。在教学的过程中我们要适度的利用例题的讲解，充分借助平面位置变化打破学生的定势思维习惯。因为三垂线定理及其逆定理都是四线相对于一个平面而言的，我们在解题的过程中，图示可能存在几个平面，那么我们应该选择一个适当的参考系进行思考。在确定二面角的平面角的过程中应用三垂线定理法，从而进一步深化三垂线定理的功能。

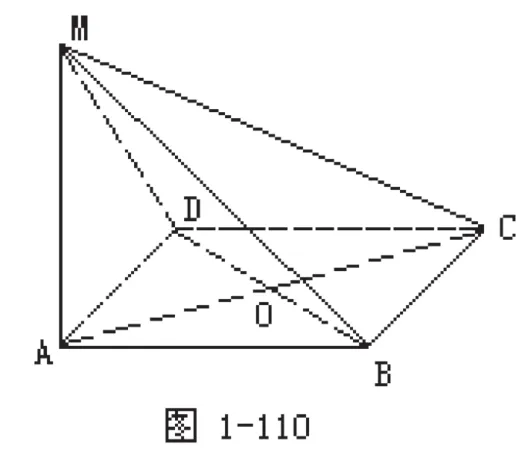
例题 如图1-110，MA⊥平面ABCD，四边形ABCD是正方形，且MA= AB=A.试求：

(1)点M到BD的距离；

所以我们应该在讲解这些知识点时，做一个适当的链接，让它们联系起来，这样，学生更容易理解知识点，并且能拓展自己的知识面，看到爪子定理，自然而然脑海中就浮现三垂线定理及其逆定理的相关概念以及相关的知识点，能在数学学习

分析：(1)首先在读题目时应该分析好已知条件是哪些，并在图纸上进行一个标注，为后面解题做好准备，拿到一道题，不要急着下手，应该先思考这道题的实质是什么，要用到什么知识点。从第一小问，我们可以分析出，要求解点M到直线BD的距离，即要求解点M到BD直线垂线长。那么我们就要试着去寻找这条垂线。从题设，我们可以看出，要求解出线线垂直，而且相对于一个平面，那么我们就可以试着构造出四线，使得可以使用三垂线定理。我们记BD线段的中点为点O，连接AO，MO，由于四边形ABCD为正四边形，就可以得到AO垂直于BD，又因为AM垂直于正四边形所在面，那么MO的射影为AO，从未得到MO垂直于BD，固线段MO为M到直线BD的距离，根据题目给出的数据就可以计量出其大小。在解题的过程中，我们需要充分的利用条件，依据题目和对图形的分析，进而理清了本题的解题思路，而本题也正是利用三垂线定理进行了解题。本题目涉及了空间想象力，学生的观察力，教师的有效引导。此题简单易上手，学生在初步感受三垂线定理的应用的同时，也减轻其学习负担。最后安排一两道类似例题，从而提升学生应用三垂线定理及其逆定理的能力，增加学生学习空间几何的信心。

(六)三垂线定理教学方法分析

本节课的教学，主要体现了建立模型、启发引导、猜想论证、学习应用、发展能力的教学思想。让学生动手做模型，教师演示指导，让学生直观地感受到空间线面、线线关系的变化。再在教师的引导下思考线面、线线垂直存在的因果关系，逐步推理，猜想命题，论证命题，从而发现定理，揭示定理的实质。对定理的应用，只要求学生在理解定理的基础上理清应用定理证题的一般步骤，学会证明一些简单问题。大部分学生认为空间几何是整个高中数学的难点，所以在教学的过程中，学生学习起来总有畏惧心理。本节课的设计，能充分的让学生感受到数学模型的魅力。安排的例题简单易懂，让学生轻松的接受，自然而然将心态放平。我们在教学的过程中，教师应该时时刻刻鼓励学生动手、动脑，时时关心学生，让学生在学习过程中与教师能建立起一种平等的关系。教学矛盾的主要方面是学生的学，学是中心，会学是目的，因此要在教学中不断指导学生学会学习。根据立体几何的教学特点，本节课主要是教给学生“动手做、动脑想、大胆猜、严格证、多训练、勤钻研”的研讨式学习方法，这样做教给了学生获取知识的途径，思考问题的方法，增加了学生的参与机会，增强了参与意识，，使学生真正能成为学习的主体。也只有这样做，才能使学生“学”有

新“思”，“思”有所“得”，“练”有新“获”，学生才会逐步感受到数学的美，会产生一种成功感，从而提高学生学习数学的兴趣；也只有这样做，才能适应素质教育下培养“创新型”人才的需要。同时本节课还应用了比较法，对三垂线定理及其逆定理进行比较，分析其相同点及其不同点，从而强化对三垂线定理与其逆定理的理解与记忆。

二、结束语

本文对高中数学的教学进行了分析和研究，通过本文的探讨，我们了解到，数学这门科学不是我们所想的那么简单的就能诠释，一堂课的好坏不是这位老师讲得有多么棒，而是在于学生学得有多么好，学得有多么自在，多么轻松，其中包含了许许多多的教学技巧。我们要深入教学的“四基”思想——基础知识，基本技能，基本思想，基本活动经验。注重学生心理的发展，在教学的过程中，要注重教学的有效性，真实性，教学要符合学生的认知水平，在整个课堂的教学中要注重学生的参与性，我们要尽量将课堂交给学生。教师掌握了学生的学习心理，便能更有效的完成教学任务，学生在学习的过程中自然而然就会表现的更轻松，学的更好。另外，在教学中我们应该充分的让学生了解本节课的教学课程实质所在，真正的把握教学内容，从而解决实际问题，进而不断的促进学生学习上的进步。

[1]邹志超，王雅倩.高中生的学习倦怠、自我效能感及其关系的研究[J].教育测量与评价 (理论版 )，2008(11)：37-38.

[2]杨丽娴，连榕.学习倦怠的研究现状及展望[J].集美大学学报，2005(6)：55-57.

[3]竺仕芳.激发兴趣，走出误区——综合高中数学教学探索[J].宁波教育学院学报，2003(04).

[4]彭然龄.普通心理学[M].北京：北京师范大学出版社，2001.

[5]周珍，周红霞，张景斌.不同认知方式中学生空间图形认知能力发展研究[J].数学教育学报，2012(6)：38-39.

[6]赵思林.“对数”定义难学的心理分析[J].数学教育学报，2012(6)：77-79.

[7]韩建军.数学教学中如何培养学生的创新意识[J].中学教学参考，2010(25).

[8]蒋建华.优化三垂线定理之管见[J].教育与管理，1993(04).