Ni3Ta的相稳定性和弹性性质的第一性原理研究

刘迦勒，宋佳齐，黄靖伟，陈佰树，李源作

（1.黑龙江八一农垦大学理学院，大庆 163319；2.东北林业大学理学院）

Ni3Ta的相稳定性和弹性性质的第一性原理研究

刘迦勒1，宋佳齐1，黄靖伟1，陈佰树1，李源作2

（1.黑龙江八一农垦大学理学院，大庆 163319；2.东北林业大学理学院）

采用基于密度泛函理论的第一性原理方法，研究Ni3Ta的四方、正交和单斜三种晶体结构的结构稳定性、弹性性质和态密度等性质。结果表明：三种晶体结构的晶格常数与实验值符合很好，其负的形成能表明Ni3Ta具有良好的热力学稳定性；Ni3Ta的结构稳定顺序是正交＞单斜＞四方，这三种结构均满足晶体的稳定性判据，B/G表明Ni3Ta具有很好的延展性。

弹性性质；第一性原理；相稳定性

目前，由于形状记忆效应和超弹性，作为功能材料的形状记忆合金引起了越来越多的注意。在形状记忆合金的实际应用中，应用最普遍的材料是TiNi合金。然而，这些合金的马氏体相变温度低于150℃，所以它们不适合应用在诸如发动机、燃气轮机和核反应的高温领域[1]。因此，非常有必要发展高温形状记忆合金。众所周知，Ni3Ta金属间化合物被认为是一种高温结构材料的增强相[2]。G.S.Firstov等研究发现Ni3Ta在改变温度的过程中经历了从高温四方结构到单斜结构的可逆转变，四方结构到单斜结构的转变认为是马氏体相变，导致了形状记忆效应[3]。在长时间的研究过程中，人们发现在不同的温度条件下Ni3Ta具有三种晶体结构：Pmmn-Ni3Ta[4]，I4/mmm-Ni3Ta[5]和P21/m-Ni3Ta[6]。哪一种晶体结构是Ni3Ta的基态结构还是不清楚。第一性原理计算方法已经广泛地用在研究材料的晶体结构、磁性和弹性等性质[7-9]。另外，众所周知，材料的相稳定性和相变行为是和它们的电子结构和弹性性质密切相关的[10，11]。因此，采用第一性原理的计算方法研究了Ni3Ta的晶体结构、弹性系数和电子结构，从微观尺度揭示了结构稳定的机制，为更好地提高它的应用价值提供了理论依据。

1 计算方法

第一性原理计算利用Materials Studio软件中的量子力学模块CASTEP（Cambridge serialtotal energy package）[12]程序包完成。离子实和价电子之间的相互作用关系由超软赝势描述。采用广义梯度近似（GGA）来处理交换关联能，交换关联势取Perdew-Burke-Ernzerhof（PBE）形式[13]。采用周期边界条件，布里渊区的特殊点积分采用Monkhorst-Pack方法[14]，四方、正交和单斜结构布里渊区K点网格数分别取8×8×10，8×10×8和5×6×5。晶体中电子波函数由平面波基组展开。平面波截断能取400 eV，迭代过程中的收敛精度为1×10-6eV。在进行各项计算前用Broden-Fletcher-Goldfarb-Shanno算法对超胞进行几何优化，以获得局域最稳定结构。结构优化时，体系的收敛标准是体系总能量收敛精度是1.0×10-5eV/atom，每个原子上的力低于0.003 eV·/nm-1，公差偏移为0.000 1 nm，应力偏差为0.05 GPa。在优化后的结构模型上，进行能量、弹性常数和态密度的计算。

2 结果与讨论

2.1 晶体结构与稳定性

通过对Ni3Ta的Pmmn，I4/mmm和P21/m的晶胞体积和原子坐标进行了优化，得到的平衡晶格常数见表1。通过表1可以看出，计算后得到的晶格常数与实验数据符合的很好，说明计算结果是可信的。比实验值略高的原因是由于采用GGA近似来处理交换关联泛函时通常会高估晶格常数。

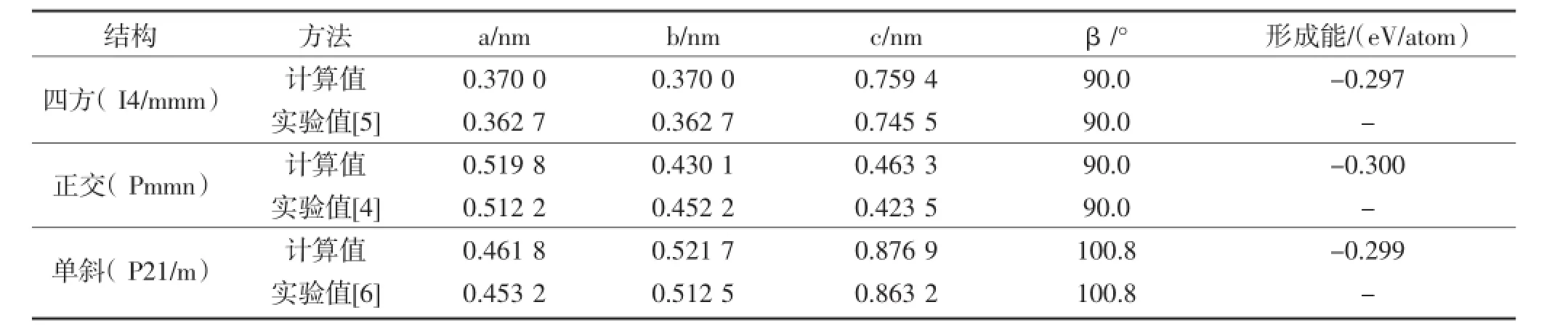
表1 Ni3Ta的计算和实验晶格常数和形成能Table 1The calculated lattice constant and formation energy of Ni3Ta in comparison with experiments

从能量角度来说，晶体的结构稳定性由形成能来决定。计算形成能的公式是

式中：Etot是晶胞的总能，ENisolid和ETasolid分别是元素Ni和Ta纯固态的单原子能量。负的形成能表明晶体结构能够稳定存在，在实验上可以形成。不同晶体结构Pmmn，I4/mmm和P21/m的形成能见表1。从表1可见，三种晶体结构四方，单斜和正交的形成能都是负的，表明Ni3Ta的这三种晶体结构都能稳定存在，这与实验是相符的。已有研究表明，形成能越低，结构越稳定。由表1可知，三种晶体结构形成能的顺序是四方＞单斜＞正交。这说明了Ni3Ta的相稳定性顺序是正交＞单斜＞四方，正交结构相对最稳定。

2.2 弹性性质

弹性系数对于理解材料的力学稳定性和弹性性质是十分必要的，很大程度上决定材料的力学行为。为了清楚力学性质，我们研究了Ni3Ta的弹性系数。利用基于胡克定律的应力-应变的方法计算了Ni3Ta的弹性系数。对于小的应变，晶体的能量为

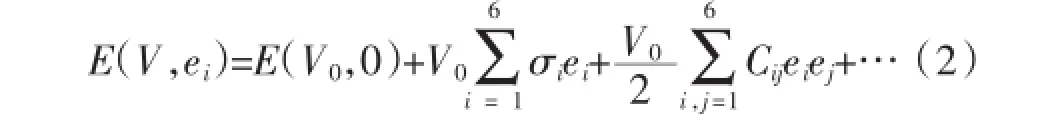
式中，V0是原始晶胞的体积，Cij是弹性系数，ei和ej是应变。晶体的独立弹性系数的数目由晶体的对称性来决定。四方结构的晶体具有6个独立的弹性系数。单斜结构的晶体具有13个独立的弹性系数正交结构的晶体具有9个独立的弹性系数。表2列出了四方、正交和单斜结构的弹性系数。对于力学稳定的四方结构、单斜结构和正交结构的晶体，它们的弹性常数必须满足以下条件[15]：

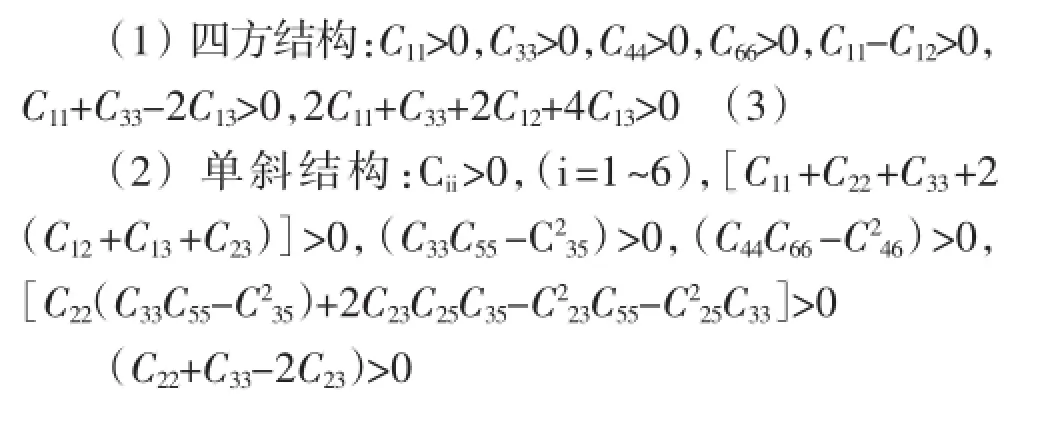
从表2计算的弹性系数可以知，四方、单斜和正交结构的弹性系数分别满足稳定性条件（3）、（4）和（5），表明三种结构在力学上是稳定的。

表2 Ni3Ta的弹性系数Cij（GPa）Table 2The elastic constants of Ni3Ta（GPa）

根据Voigt-Reuss-Hill（VRH）模型通过弹性系数可以得到多晶材料的体模量、切变模量等弹性性质[16]。计算多晶体材料体模量B和切变模量G的计算式为

另外，杨氏模量（E）和泊松比（v）可用以下公式进行计算：

Pugh等提出可用材料的体模量与剪切模量的比值B/G表示材料的脆性和延展性的力学行为。材料的体模量与剪切模量的比值B/G越大，则其延性越大，反之则脆性越好。B/G值大于1.75对应着材料的延展性，B/G值小于1.75对应着材料的脆性[17]。表3结果表明，Ni3Ta是延展性材料。

表3 Ni3Ta的弹性模量（GPa）和泊松比Table 3The elastic modulus（GPa）and Poisson’s ratio of Ni3Ta

2.3 电子结构

为了揭示不同晶体结构稳定性的物理本质，计算了四方、正交和单斜晶体结构的总态密度和分波态密度，结果如图2所示。图中0eV处的实线表示费米（Fermi）能级的位置。一般来说，费米能级处态密度的数值N（EF）决定着材料的结构稳定性，费米能级处态密度的数值N（EF）越低，材料结构越稳定。四方、单斜和正交结构在费米能级处态密度的数值N（EF）分别是2.84 eV-1、2.07 eV-1、1.70 eV-1。所以，Ni3Ta合金中四方结构是最不稳定的。相对四方结构来说，单斜和正交结构更稳定，而正交结构是最稳定的。这与前面提到的形成能计算结果是一致的。

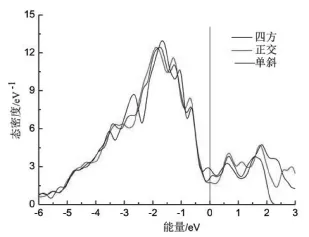
图1 Ni3Ta的总态密度Fig.1The total density of states of Ni3Ta

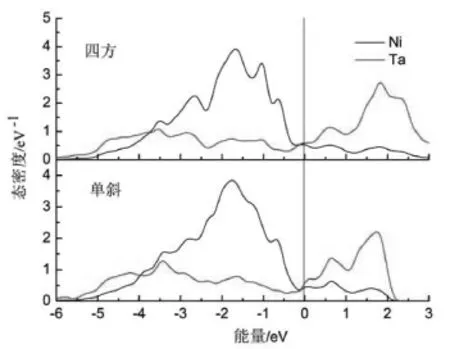
图2 Ni3Ta的四方和单斜结构各原子的分波态密度Fig.2The partial density of states of Ni3Ta with thetetragonal and monoclinic phases

为了从电子结构的角度进一步研究四方到单斜结构相变的本质，四方和单斜结构分波态密度也被给出。从图2中可看到，低于费米能级的总态密度主要是Ni3d轨道的贡献，而高于费米能级的总态密度的贡献主要来源于Ta的5d电子。然而，Ni3d电子和Ta5d轨道分别在较高能级和较低能级对总态密度有一定的贡献，表明了Ni3d和Ta5d轨道之间具有杂化作用。所以，Ni3d和Ta5d轨道之间的杂化作用决定着Ni3Ta合金的结构稳定性。

3 结论

利用第一性原理的方法计算研究了Ni3Ta的四方、正交和单斜结构的结构、弹性和态密度等性质。研究结果表明，Ni3Ta的晶体结构参数与实验值符合的很好。Ni3Ta具有热力学稳定性，在弹性性能方面表现出优良的延展性能。Ni3Ta的四方、正交和单斜结构在力学上都是稳定的。计算的态密度结果证明，Ni3d态和Ta5d态杂化作用是Ni3Ta结构稳定的主要原因。

［1］Otsuka K，Ren X.Physical metallurgy of Ti-Ni-based shape memory alloys［J］.Prog.Mater.Sci.，2005，50:511-678.

［2］Jena A K，Chaturvedi M C.The role of alloying elements in the design of nickel-base superalloys［J］.J.Mater.Sci.， 1984，19（10）：3121-3139.

［3］Firstov G S，Koval Y N，Van H J，et al.Martensitic transformation and shape memory effect in Ni3Ta:A novel hightemperatureshapememoryalloy［J］.Mater.Sci.Eng.A，2008，42：590-593.

［4］Giessen B C，Cohen M，Grant N J.Metastable hexagonal close-packed phases in Ni-rich Ni-Nb and Ni-Ta alloys［J］.J.Less-Common Metals，1967，13：611-618.

［5］Nowotny H，Oesterreicher H.Die Kristallstrukturen von β-TaNi3，Ta（Cu，Al）2，Nb（Cu，Al）2und Ta6（Cu，Al）7［J］. Monatsh.Chem.，1964，95（3）：982-989.

［6］Zhao J T，Gelato L，Parthe E.Structure refinement of monoclinic 12-layer TaNi3withβ-NbPt3type-New crystallographic descriptions of this type and of the Nb3Rh5type based on smaller unit cells［J］.Acta Crystallogr.，C，1991，47：479-483.

［7］胡飞，陈佰树，吴坤，等.TiNiZr高温形状记忆合金的马氏体相变和相稳定性的理论研究［J］.黑龙江八一农垦大学学报，2015，27（2）:79-82.

［8］唐春红，林长圣，刘培生.Fe掺杂BaTiO3后铁电铁磁性质的第一性原理［J］.河南科技大学学报：自然科学版，2013，34（4）:95-97.

［9］王春香，陈佰树，孙志，等.Heusler合金Mn2NiSi的形状记忆行为和磁性研究［J］.河南科技大学学报：自然科学版，2015，36（1）:92-95.

［10］Lv Z Q，Zhang F C，Sun S H，et al.First-principles study on the mechanical，electronic and magnetic properties of Fe3C［J］.Comput.Mater.Sci.，2008，44:690-694.

［11］Tao X M，Chen H M，Tong X F，et al.Structural，electronic and elastic properties of V5Si3phases from first-principles calculations［J］.Comput.Mater.Sci.，2012，53:169-174.

［12］Segall M D，Lindan P J D，Probert M J，et al.First-principles simulation：ideas，illustrations and the CASTEP code［J］.J Phys Condens Matter，2002，14：2717-2744.

［13］Perdew J P，Burke K，Ernzerhof M.Generalized Gradient Approximation Made Simple［J］.Phys Rev Lett，1996，77：3865-3868.

［14］Monkhorst H J，Pack J D.Special points for Brillouin-zone integrations［J］.Phys Rev B，1976，13：5188-5192.

［15］Nye J F.Physical Properties of Crystals［M］.Oxford：Oxford University Press，1985.

［16］Hill R.The elastic behaviour of a crystalline aggregate［J］. Proc Phys Soc，1952，65：349-354.

［17］Pugh S F.Relations between the elastic moduli and the plastic properties of polycrystalline pure metals［J］.Phil Mag，1954，45：823-843.

First Principles Study of Phase Stability and Elastic Properties of Ni3Ta

Liu Jiale1，Song Jiaqi1，Hang Jingwei1，Chen Baishu1，Li Yuanzuo2
（1.College of Science，Heilongjiang Bayi Agricultural University，Daqing 163319；2.College of Science，Northeast Forestry University）

The structural，elastic properties and density of states of Ni3Ta alloy with the tetragonal，orthorhombic and monoclinic structures were investigated by the first-principles calculations based on density functional theory.The lattice constants of the three structures were in good accordance with the experimental results.The results showed that the negative formation energy indicated Ni3Ta was stable thermodynamically.the predicted phase stability trend was orthorhombic＞monoclinic＞tetragonal from the calculated formation energy and density of states.These three structure met the stability criterion of crystal，B/G indicated Ni3Ta had good ductility.

elastic properties；first principles；phase stability

TG146.2

A

1002-2090（2017）01-0136-04

2016-03-03

国家自然科学基金项目（11404055）；黑龙江省自然科学基金（QC2013C006）；黑龙江省大学生创新创业训练计划项目（201510223028）。

刘迦勒（1994-），女，黑龙江八一农垦大学理学院2014级信息与计算科学专业在读本科生。

陈佰树，男，讲师，E-mail:bschen@126.com。