随机车流作用下大跨度悬索桥振动分析

殷新锋+丰锦铭+刘扬+蔡春声

摘 要：引入元胞自动机随机车流模拟方法，采用已建立的能考虑车辆空间振动的18个自由度整车模型模拟车流中重型车辆，利用单自由度车辆模型模拟车流中其他车型，模拟了能考虑邻近车辆对车流的影响桥上随机车流模型.通过车轮与桥面间的变形与接触力协调关系，建立了桥梁与车流耦合作用下运动方程.分析表明：车流中相邻车辆是否考虑对桥梁振动位移的影响较大，且随机车流作用下引起的悬索桥主梁及索塔的空间振动不能被忽视.

关键词：桥梁；振动；车流；桥面不平整度

中图分类号：TU311.3；TU352.1 文献标志码：A

在研究桥梁车辆耦合振动时，以往大多数研究人员主要考虑桥梁在移动车辆荷载作用下的竖向振动.近年来，研究人员开始分析移动车辆荷载作用下桥梁横向振动[1-3].然而，以往研究都忽略汽车引起的横向及纵向力对桥梁的作用，进而在多数研究中忽略了桥梁在随机车流作用下的横向和纵向振动.对于像悬索桥这种大跨度桥梁来说，忽略桥梁在随机车流下的三维振动可能会导致与实际情形不符[4-5].

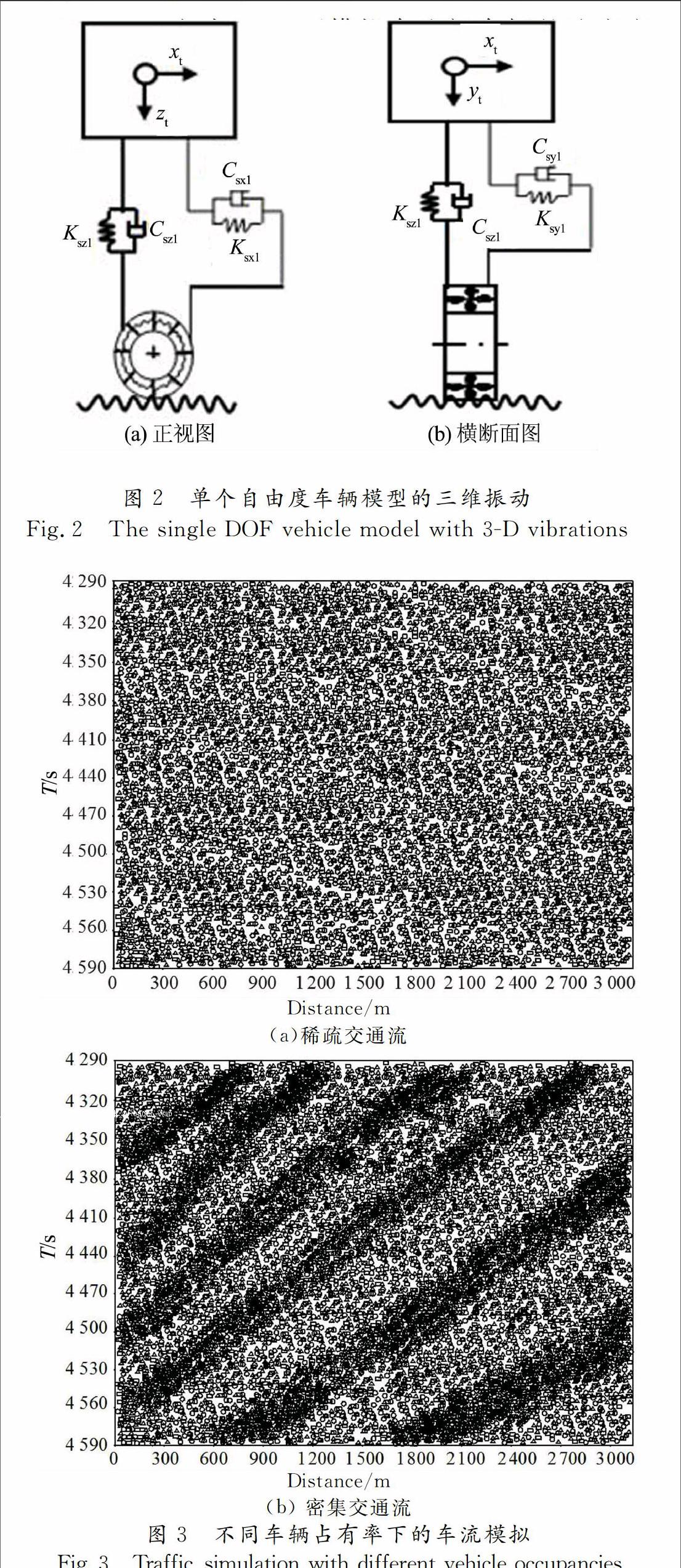
在现有随机车流作用下桥梁振动的研究中，常将随机车流简化为既定的多车辆分布模式 [6-7].对于大跨度桥梁而言，这样的简化并不能准确预测实际车辆的动态性能[8].基于元胞自动机的随机车流模拟，由于其可分析车流行驶状态中各车辆的随机特征，而逐渐引起研究者的重视并被用于分析道路或桥梁上车流分布特征，但较少用于车流作用下桥梁振动的研究领域[9-10].

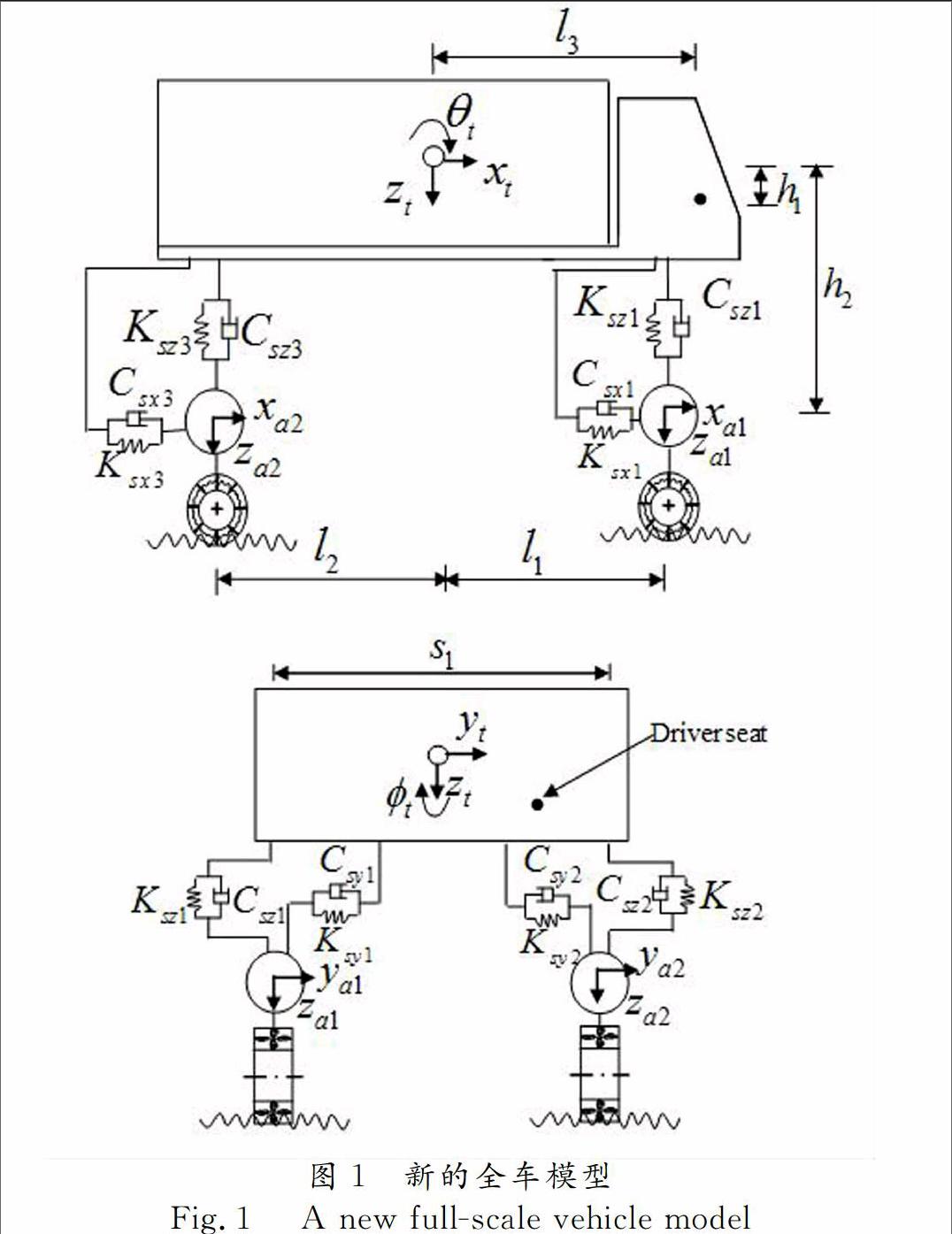
基于已建立的能考虑车辆三向振动的18个自由度整车模型，引进了改进的元胞自动机模型并考虑邻近车辆对车流的影响.通过车轮与桥面间的变形与接触力协调关系，建立了桥和车流耦合作用运动方程.数值分析表明：本文提出的车桥耦合模型能合理研究大跨度悬索桥在随机车流下的空间振动.

1 车流桥梁耦合系统的研究方法

1.1 车辆模型运动方程

2.3 车流中是否考虑邻近车流影响的比较

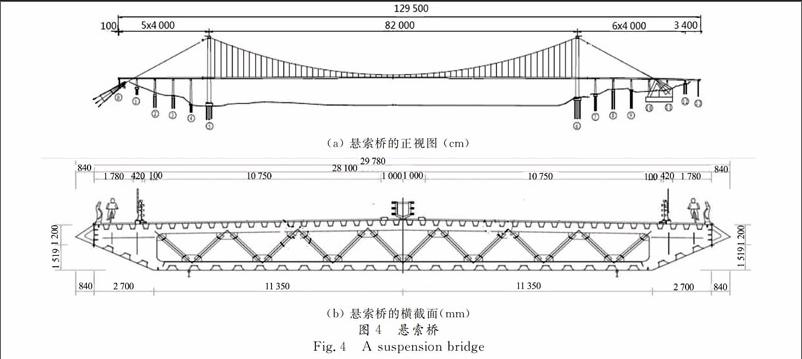
下列分析中，桥面粗糙度等级为好，交通流占有率分别为畅通交通流量ρ=0.07，稀疏交通流量ρ=0.15和密集交通流量ρ=0.3 三种.桥梁的三维动态响应分析结果如图6～图10所示.

图6为两种典型车流作用下加劲梁跨中和四分之一跨处的竖向位移时程曲线.由图可知，考虑邻近车流影响时所对应的最大竖向位移值小于不考虑邻近车辆影响时所对应的最大竖向位移.如本例中，跨中最大豎向位移在不考虑邻近车流影响和考虑邻近车流影响下所对应梁的最大值分别为12.11 cm及15.02 cm.该现象也许是由于考虑邻近车辆的影响，车流中的车速与车间距发生变化所致.

3 结 论

基于已建立的能考虑车辆三向振动的18个自由度整车模型，引进改进的元胞自动机模型并考虑邻近车辆对车流的影响，通过车轮与桥面间的变形与接触力协调关系，分析了车流作用下悬索桥的振动响应.数值分析表明：

1）本文提出的桥梁车流耦合模型能合理研究大跨度悬索桥在随机车流下的空间振动.

2） 随机车流作用下，未考虑邻近车辆影响时所对应的桥梁位移大于考虑邻近车辆影响时对应的桥梁位移值，如跨中最大竖向位移在不考虑邻近车流影响为12.11 cm，而考虑邻近车流影响下所对应的最大值为15.02 cm.因此，车流中相邻车辆考虑与否对桥梁振动位移的影响不能被忽视.

3） 随机车流作用下引起的悬索桥主梁及索塔的空间振动不能被忽视.如主梁的纵向位移可达5.33 cm，该位移可能会加速桥梁末端伸缩缝的损坏；塔顶纵向位移可达12.03 cm，该位移值会增加悬索桥的缆索及索塔结构的附加应力，从而加速结构损坏，在设计中应被足够重视.

4） 悬索桥振动响应随在桥面条件等级变差而增加.如桥面状况等级由好变差时，跨中最大竖向位移由20.61 cm增加到24.35 cm.因此，桥面条件对于桥梁振动具有很大的影响，桥面的定期保养也是减少车辆及桥梁振动的有效方法.

参考文献

[1] CHANG D， LEE H. Impact factors for simplespan highway girder bridges [J]. Journal of Structural Engineering， 1994， 120（3）： 704-715.

[2] HUANG D Z， WANG T L. Impact analysis of cablestayed bridges [J]. Computers and Structures， 1992， 43（5）： 897-908.

[3] CHEN Y B， FENG M Q. Modeling of traffic excitation for system identification of bridge structures [J]. ComputerAided Civil and Infrastructure Engineering， 2006， 21（2）： 57-66.

[4] JIANG J Q. Transient responses of Timoshenko beams subject to a moving mass [J]. Journal of Vibration and Control， 2011， 17（13）： 1975-1982.

[5] 韩万水，陈艾荣. 随机车流下的风汽车桥梁系统空间耦合振动研究[J].土木工程学报， 2008，41（9）：97-102.

HAN Wanshui， Chen Airong. Three dimensional coupling vibration of windvehiclebridge systems under random traffic flow [J]. China Civil Engineering Journal， 2008，41 （9）：97-102. （In Chinese）

[6] CHEN S R， WU J. Modeling stochastic live load for longspan bridges based on microscopic traffic flows simulation [J]. Computers and Structures， 2011， 89（9）： 813-824.

[7] DENG L， CAI C S. Development of dynamic impact factor for performance evaluation of existing multigirder concrete bridges [J]. Journal of Structural Engineering， 2010， 32（1）： 21-31.

[8] YIN X F， FANG Z， CAI C S. Lateral vibration of highpier bridges under moving vehicular loads [J]. Journal of Bridge Engineering， 2011，16（3）： 400-412.

[9] ZHANG W， CAI C S. Fatigue reliability assessment for existing bridges considering vehicle speed and road surface conditions [J]. Journal of Bridge Engineering， 2012， 17（3）： 443-453.

[10]韩万水，马麟，院素静，等.桥面粗糙度非一致激励对车桥耦合振动系统响应影响分析[J].土木工程学报，2011，44（10）：81-90.

HAN Wanshui， MA Lin， YUAN Sujing， et al. Analysis of the effect of inconsistent stimulus of surface roughness on vehiclebridge coupling vibrations [J]. China Civil Engineering Journal， 2011， 44（10）：81-90. （In Chinese）

[11]KONG X J， GAO Z Y， LI K P.A two lane celluar automata model with influence of next nearest neighbor vehicle[J]. Communications in Theoretical Physics， 2006，45（4）： 657-662.

[12]彭献， 殷新锋， 方志. 变速车辆与桥梁的耦合振动及其TMD控制[J]. 湖南大学学报：自然科学版， 2006， 33（5）： 61-66.

PENG Xian， YIN Xinfeng， FANG Zhi. Vibration and TMD control of coupled system of girder bridge and vehicle with variable speeds[J]. Journal of Hunan University： Natural Sciences， 2006， 33（5）： 61-66. （In Chinese）

[13]蒋望，邵旭东，彭旺虎，等.独塔悬索橋基本参数研究[J]. 湖南大学学报：自然科学版， 2011， 38（6）： 13-19.

JIANG Wang， SHAO Xudong， PENG Wanghu， et al. Research on suspension bridges with a singletower[J]. Journal of Hunan University： Natural Sciences， 2011， 38（6）： 13-19. （In Chinese）